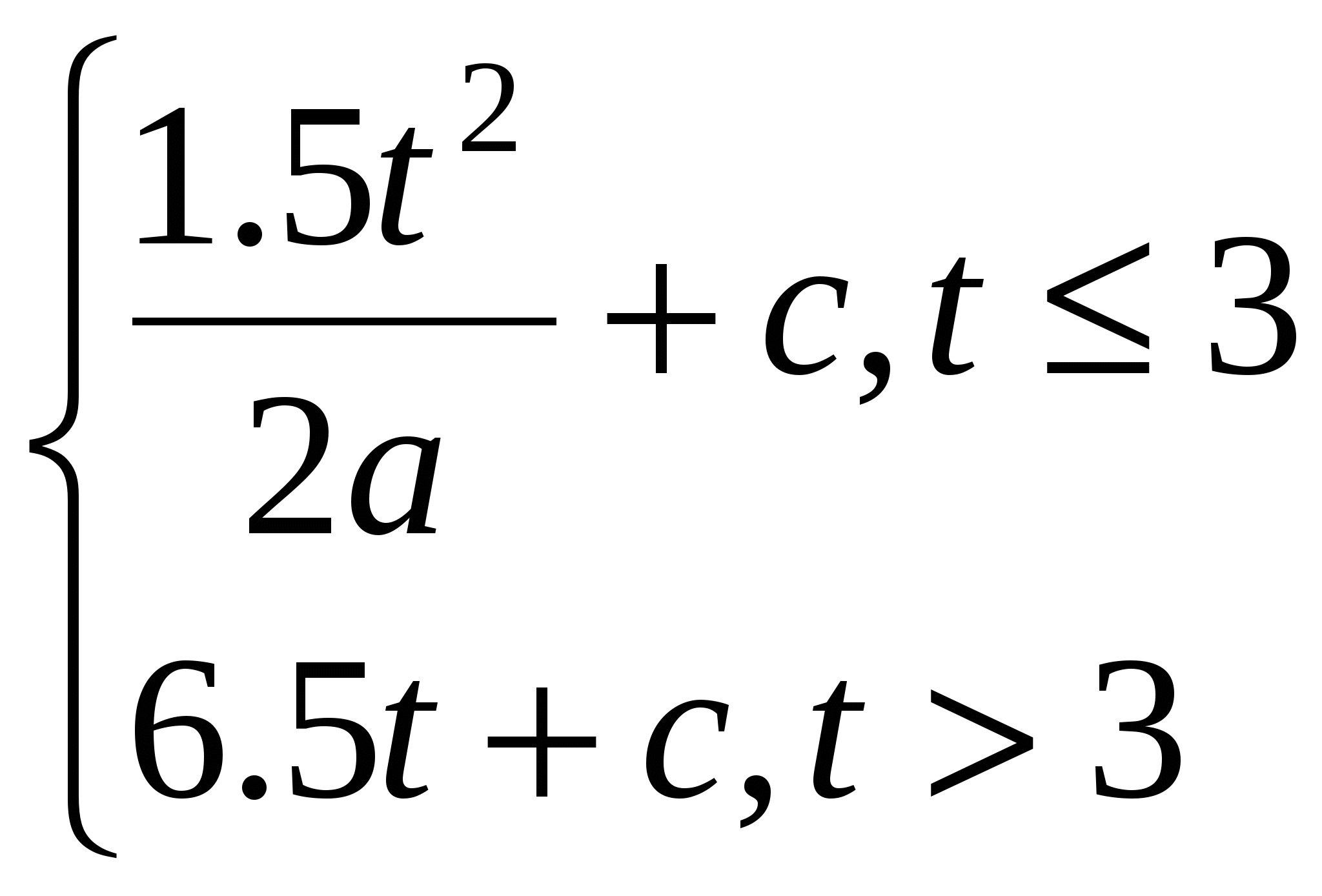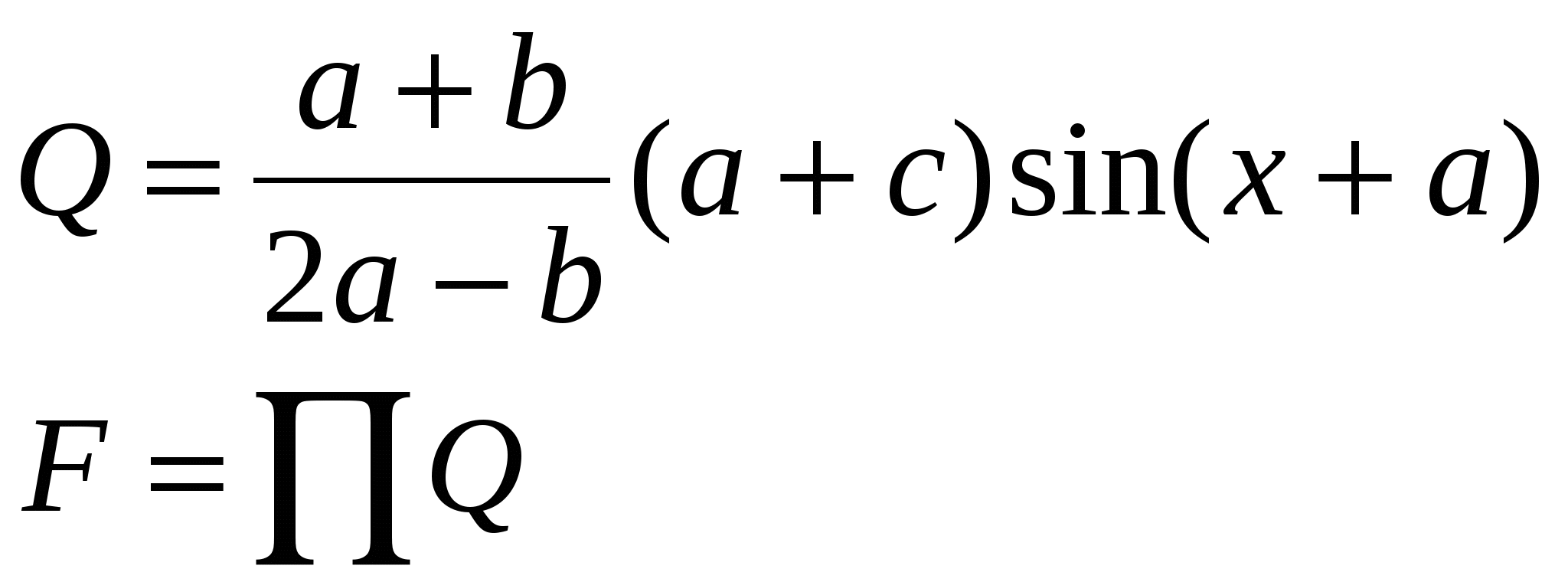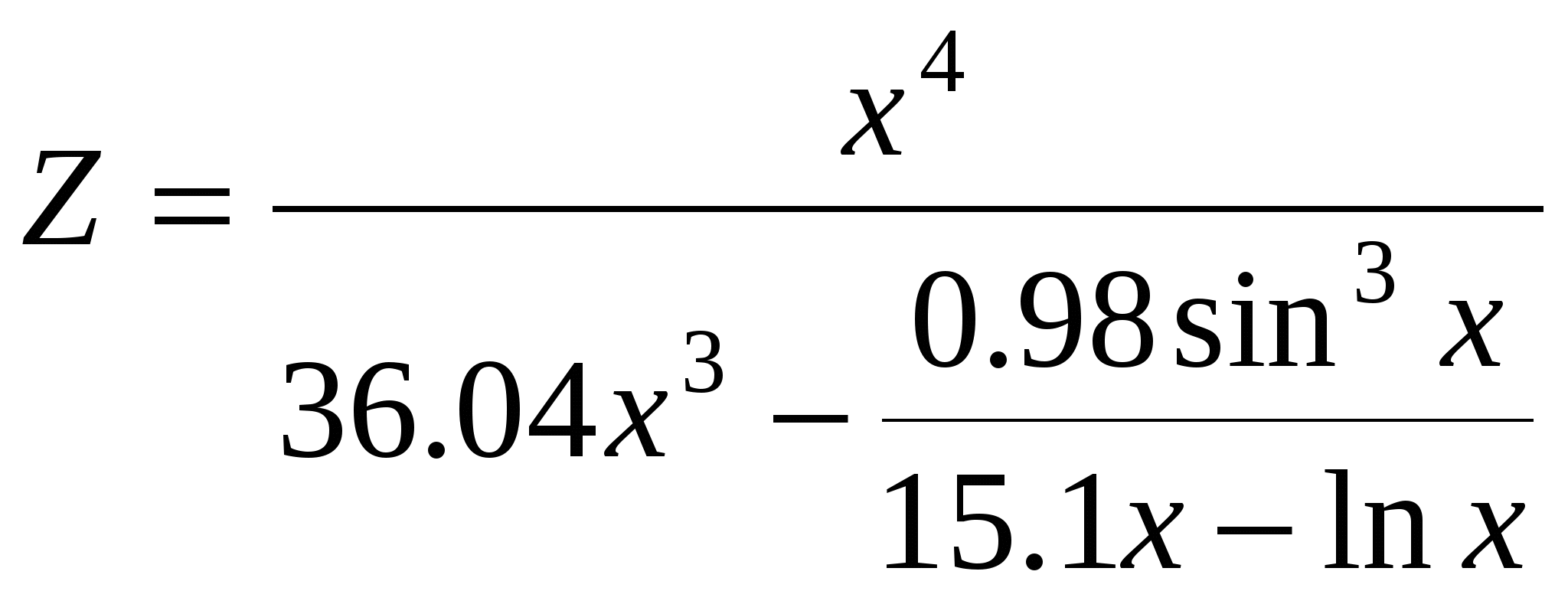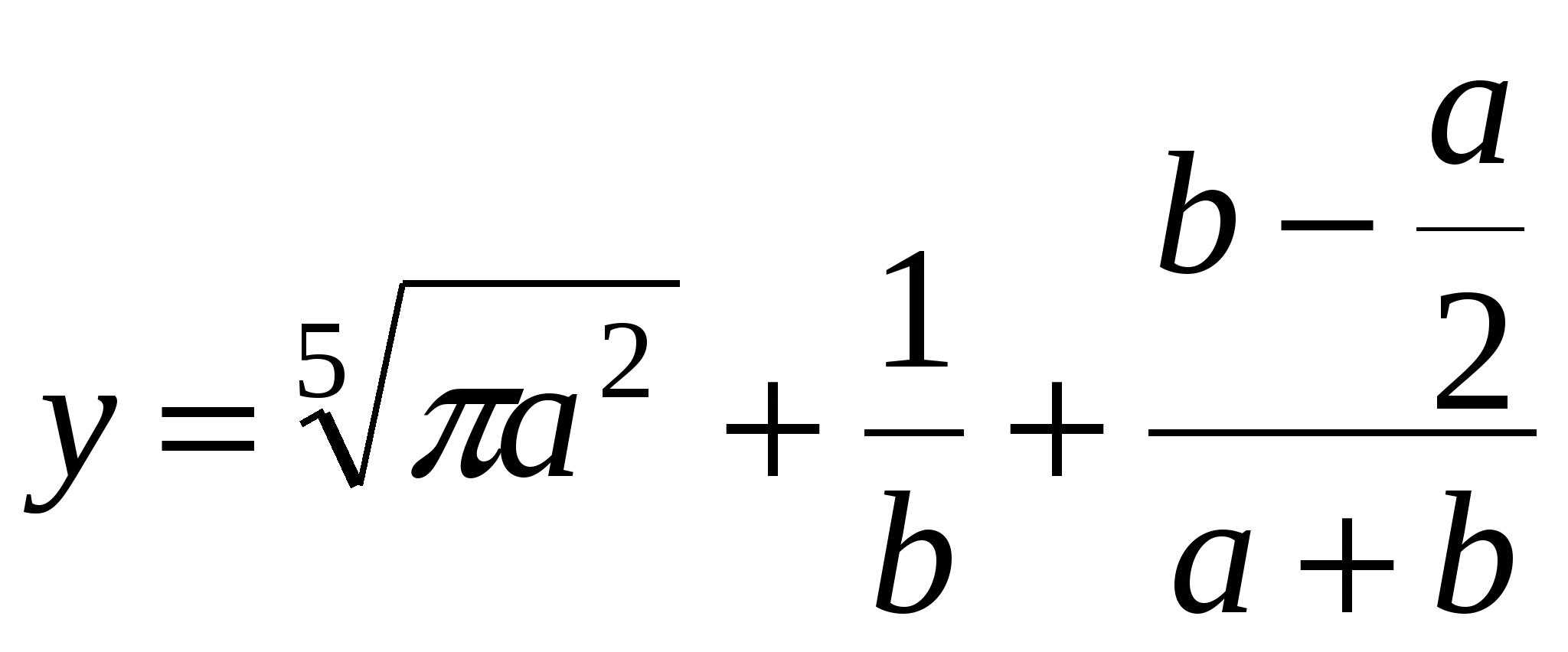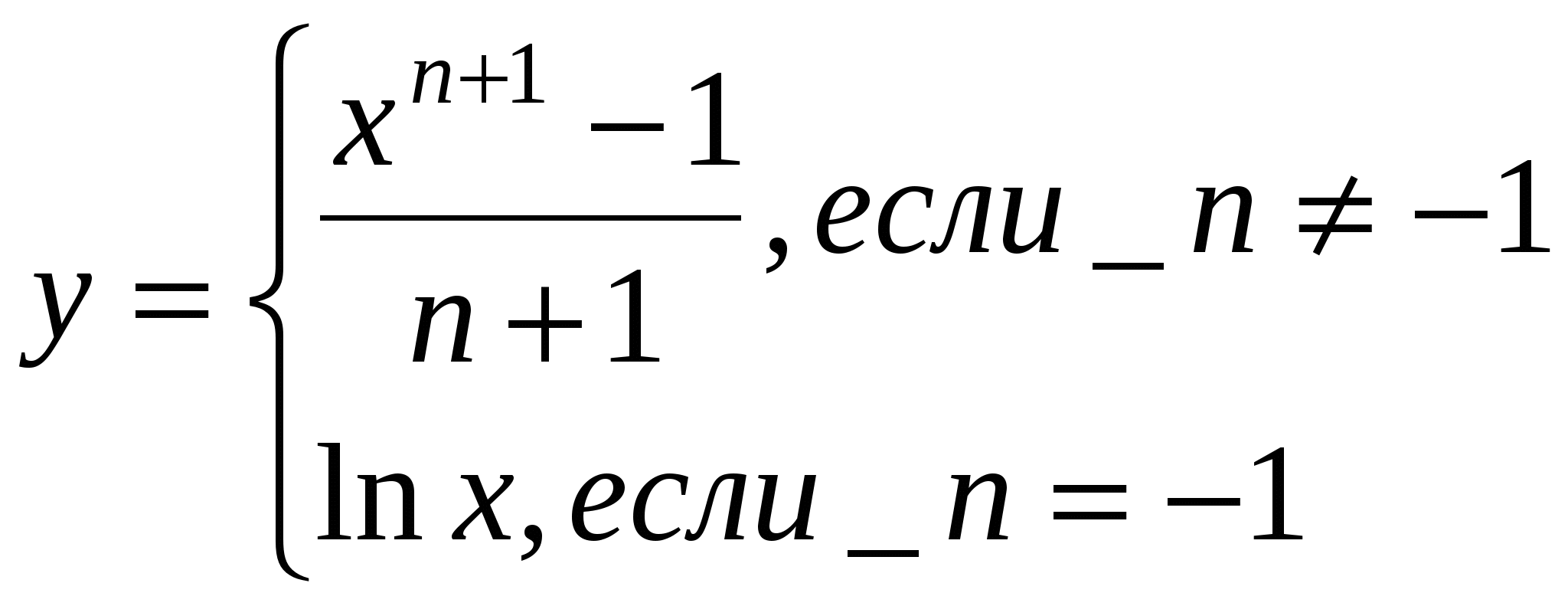Задание № 3. Организация циклов
Задание. Составить блок-схему алгоритма и программу решения поставленной задачи, которая в соответствии с исходными данными вычисляет значения заданных выражений.
Пример. Составить алгоритм и программу для вычисления y, при всех значениях x, начинающихся с начального xn > 0, и изменяющихся с шагом 0.6. Вычислять y, пока подкоренное выражение ≥0.1. Найти количество вычисленных y.
Б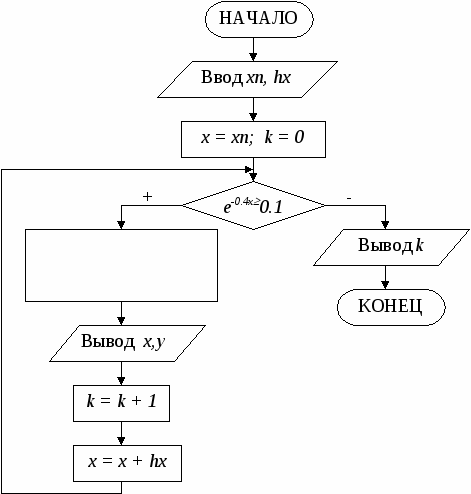 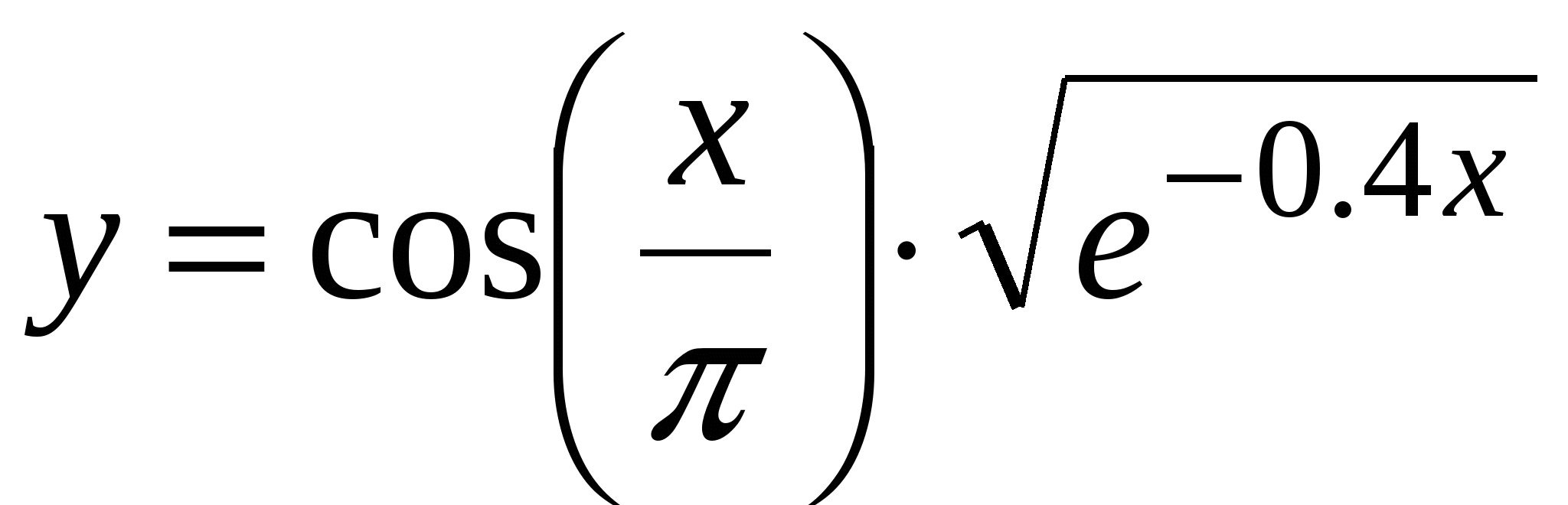
лок-схема алгоритма:
Программа на языке Турбо Паскаль:
Program Pr3;
Var x, xn, hx, y: real; k : integer;
Begin
Write(‘Ввод xn, hx ’); Readln(xn, hx);
x:=xn; k := 0;
While Exp(-0.4 * x) >= 0.1 do Begin
y := cos(x / Pi ) * Sqrt(Exp(-0.4 * x));
writeln(‘x=’, x : 6 : 2, ‘ y=’, y : 6 : 2);
k := k + 1; x := x + hx; End;
writeln(‘k=’, k); End.
Варианты заданий.
№
п/п
|
Модель
|
Исходные данные
|
Выводимые
данные
|
1
|
2
|
3
|
4
|
1
|
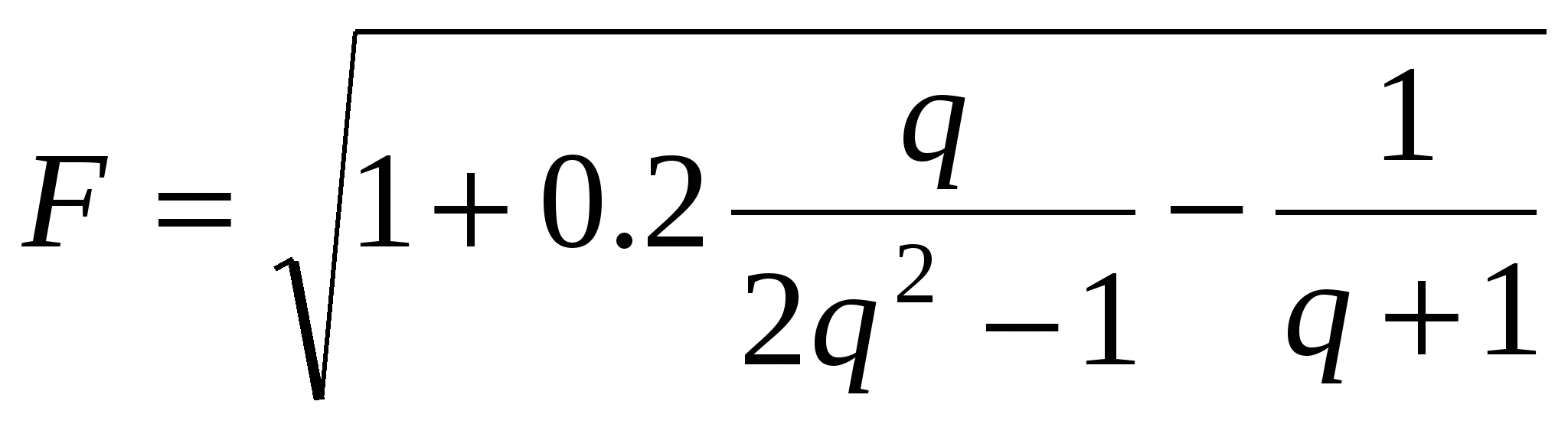
Считать F до тех пор, пока подкоренное выражение >0.
|
q ≤ 3
hq=-0.2
|
F, q.
Количество вычисленных F.
|
2
|
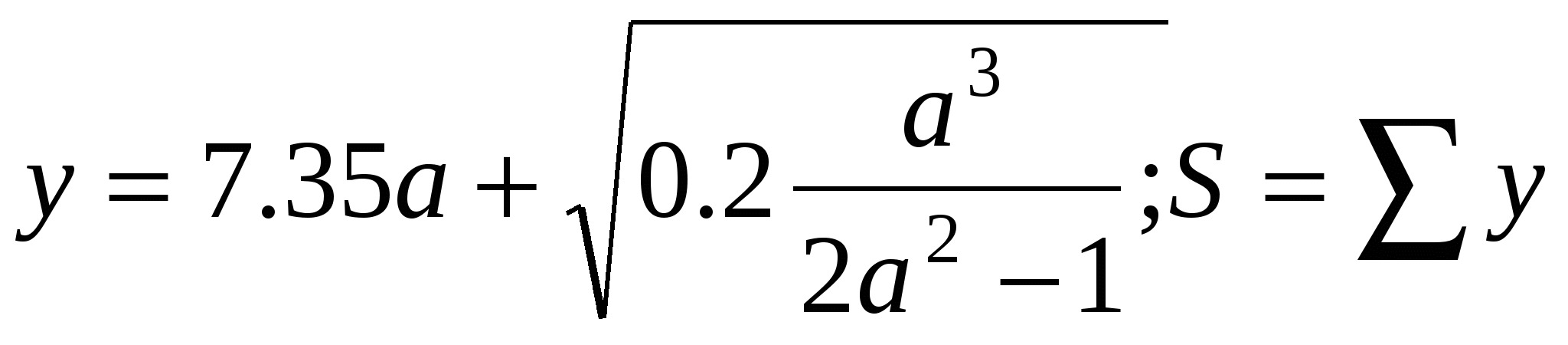
Считать у до тех пор, пока выражение под знаком корня > 1.
|
a ≤ 7
ha=-0.5
|
y, a, S.
Количество вычисленных y.
|
3
|
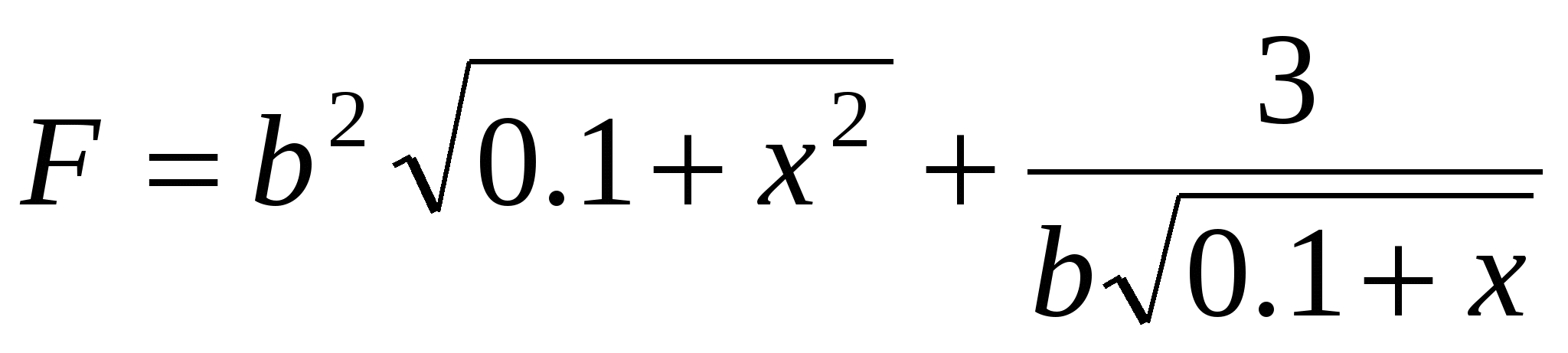 S=F S=F
Считать F пока не превысит А.
|
b, A
x≥0
hx=0.5
|
x, F, S.
Количество слагаемых в сумме.
|
4
|
F=2.72y+2Z2sin(x+y) x=a2-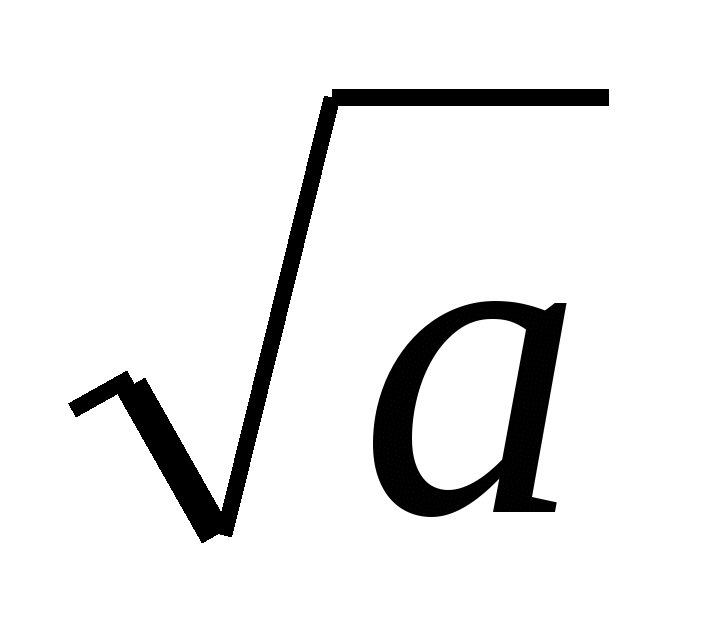
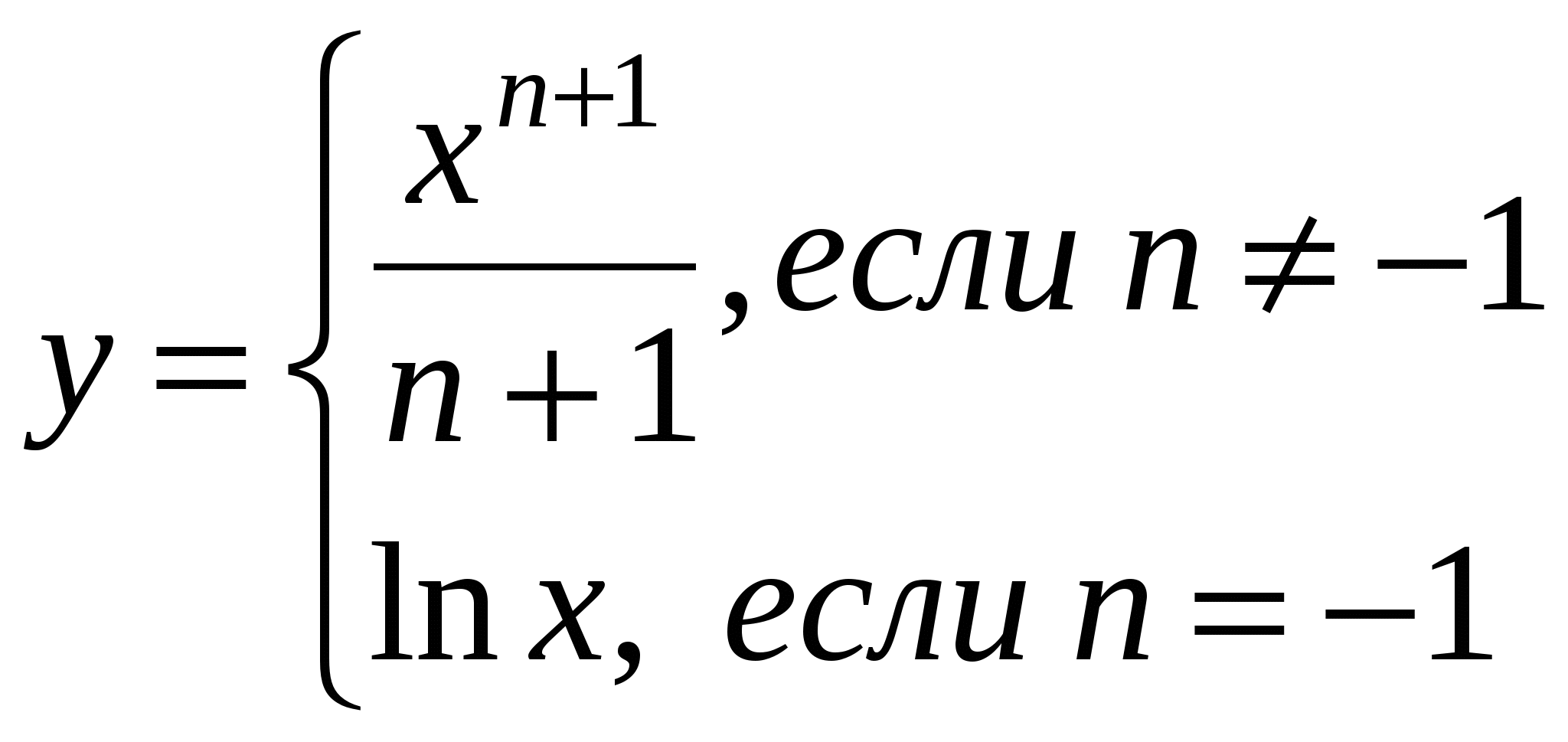 Считать F до тех пор, пока F остаётся меньше 100. Считать F до тех пор, пока F остаётся меньше 100.
|
a, n,
Z ≥0.4
hz = 0.5
|
x, y, F, Z .
Количество вычисленных F.
|
5
|
f=t3ln Z+1 Z=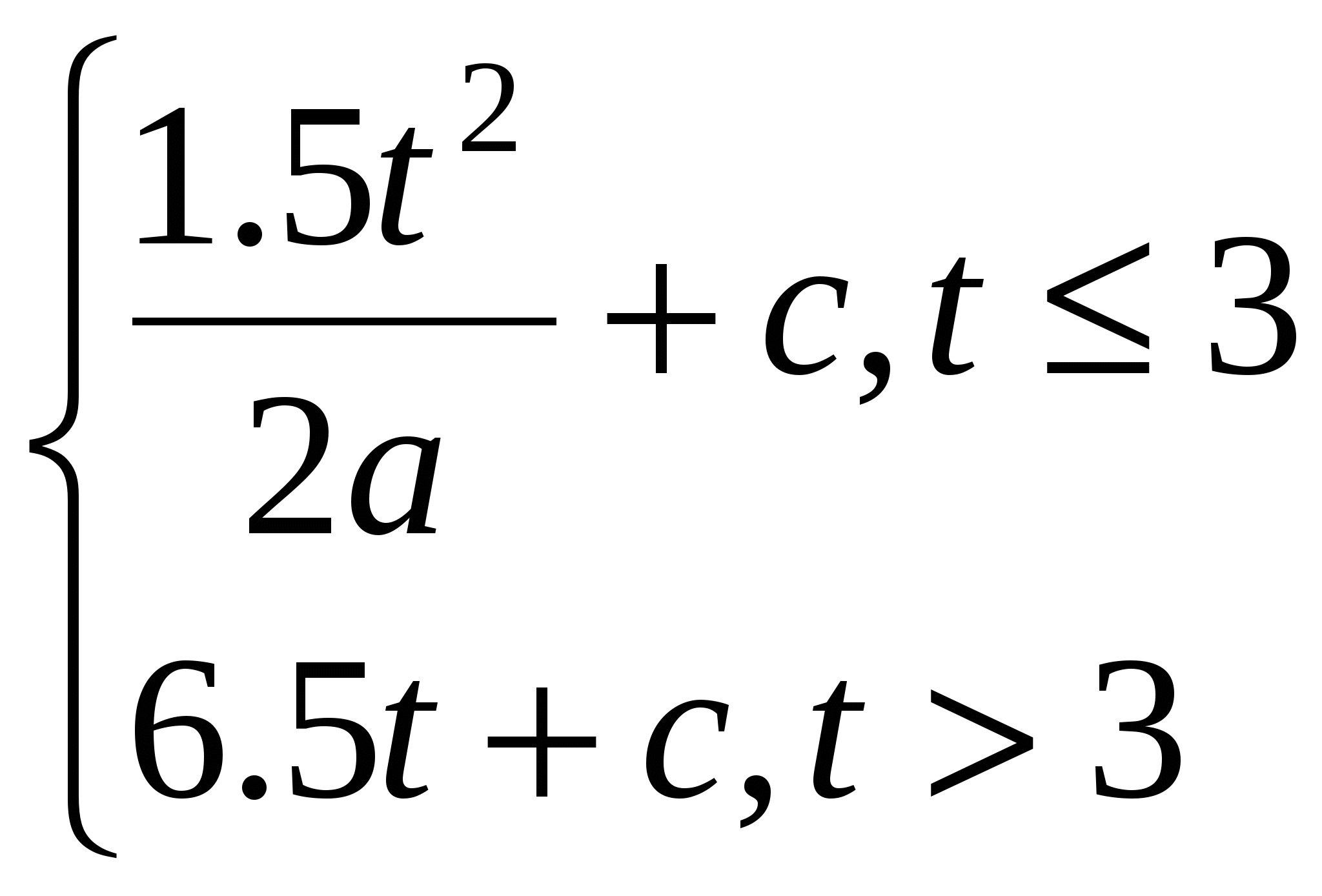
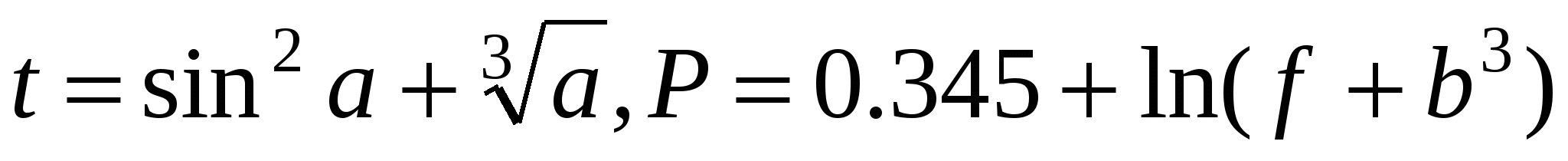
Считать P, пока (f+b3)>0.
|
c,a
b ≤ 2
hb=-0.2
|
t, Z, f, b, P.
Количество вычисленных P.
|
6
|
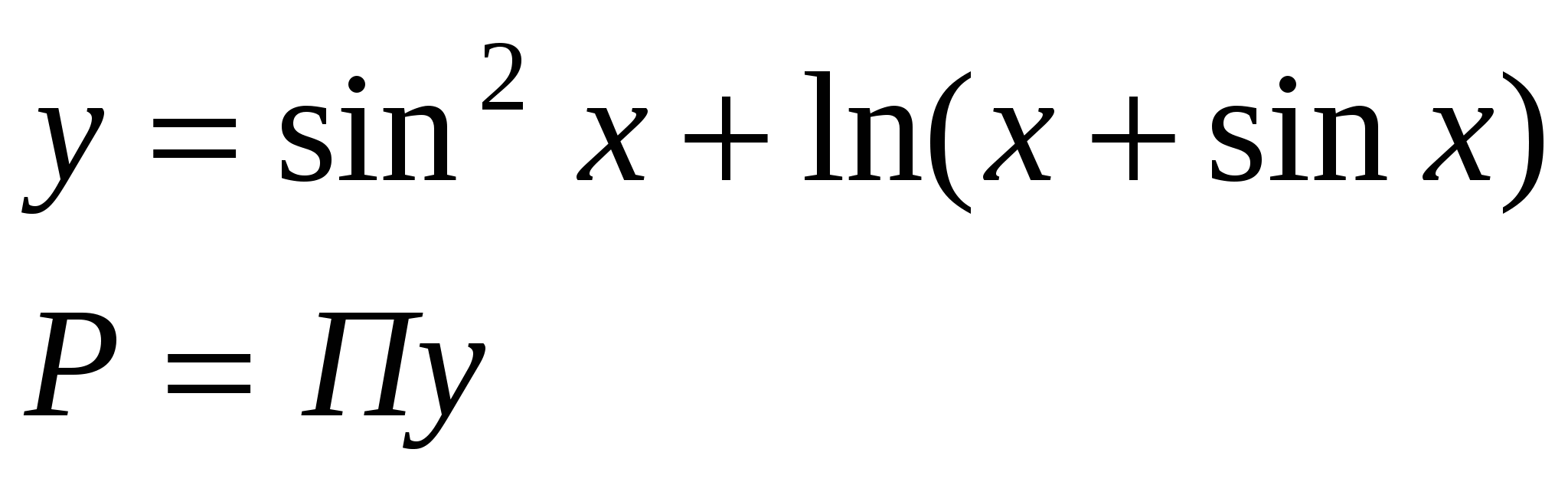
Считать P, до тех пор, пока станет > Q.
|
Q,
x ≥1
hx=0.5
|
x, y, P.
Сумма и количество положительных значений y.
|
7
|
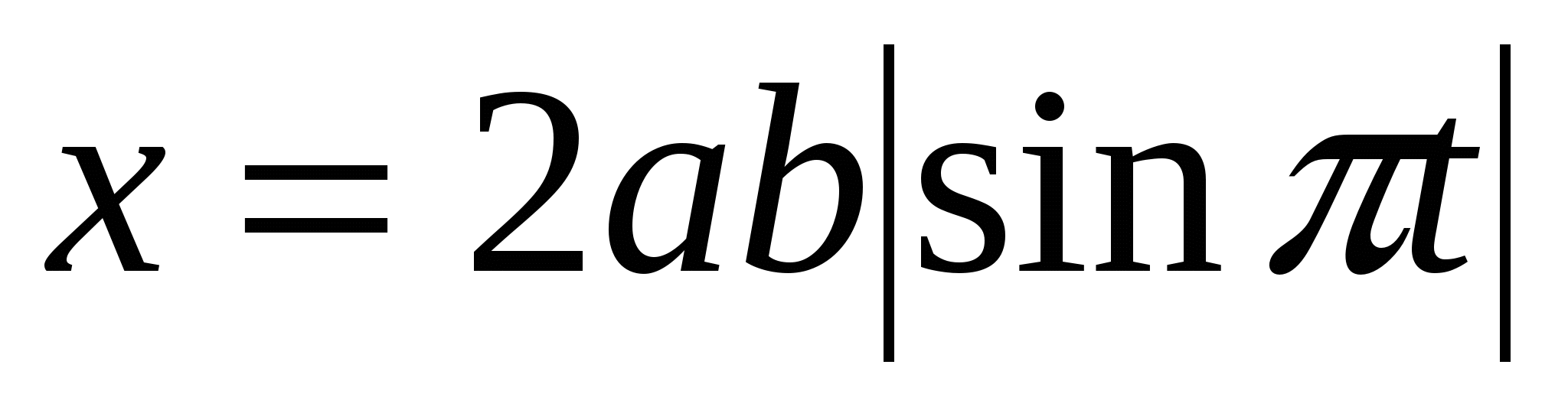 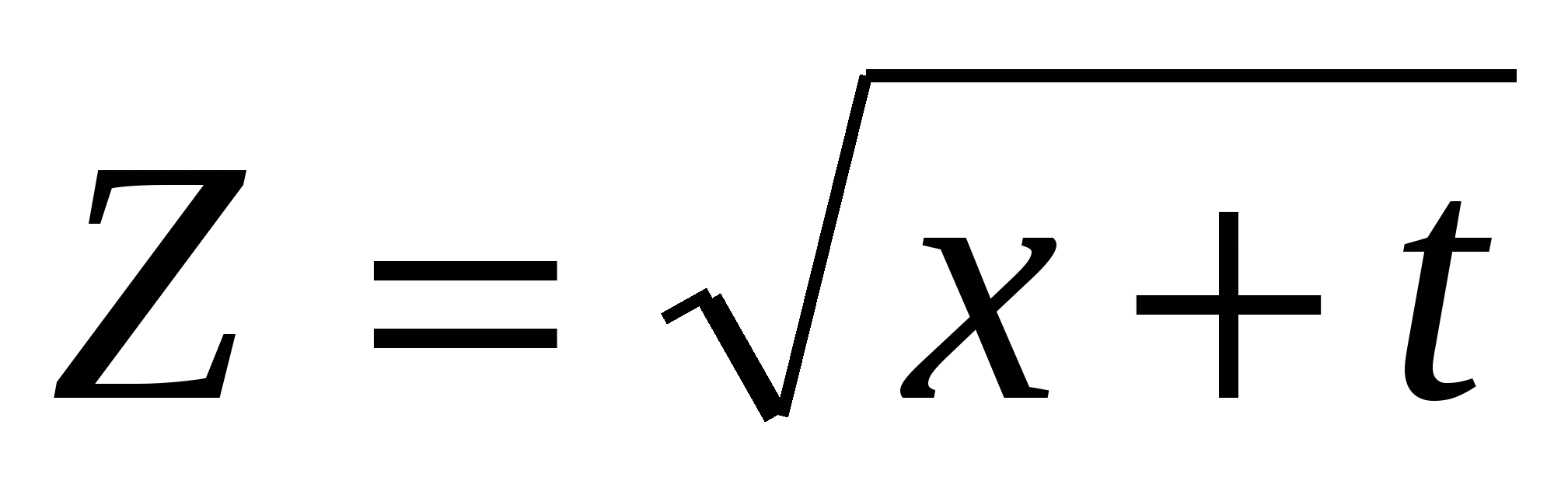
M=K!, где К- количество Z.
Считать Z, пока выражение x+t≥0.
|
a, b,
t ≤ 5
ht=-0.5
|
t, x, Z, M, K.
|
Продолжение таблицы к заданию 3
1
|
2
|
3
|
4
|
8
|
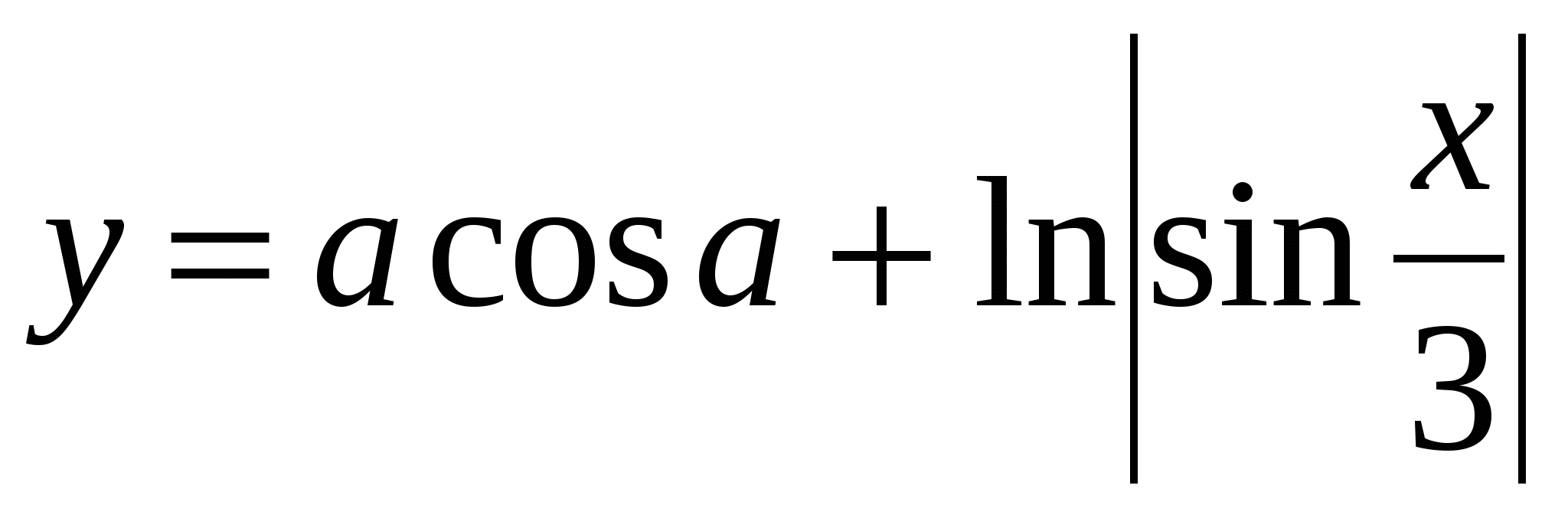
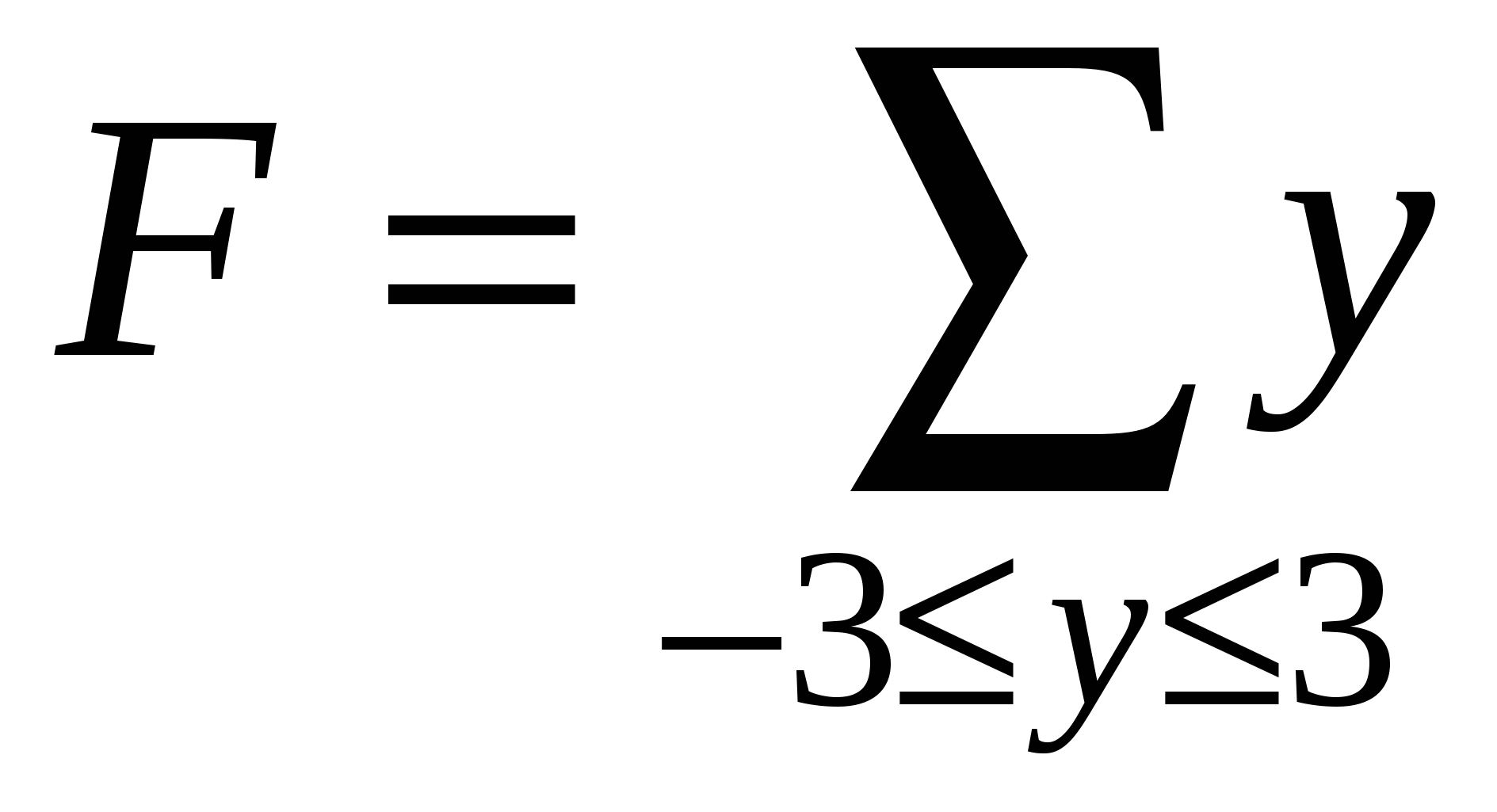
Считать F, пока значение F
|
x, Q,
a≥0
ha=0.5
|
y,a,F.
Количество слагаемых в сумме.
|
9
|
F=5.37x + ln(x3+x2+x)
P= F
Считать F до тех пор, пока выражение под знаком логарифма > 0.
|
x ≤ 3
hx=-0.1
|
F, x, P.
Количество сомножителей в P.
|
10
|
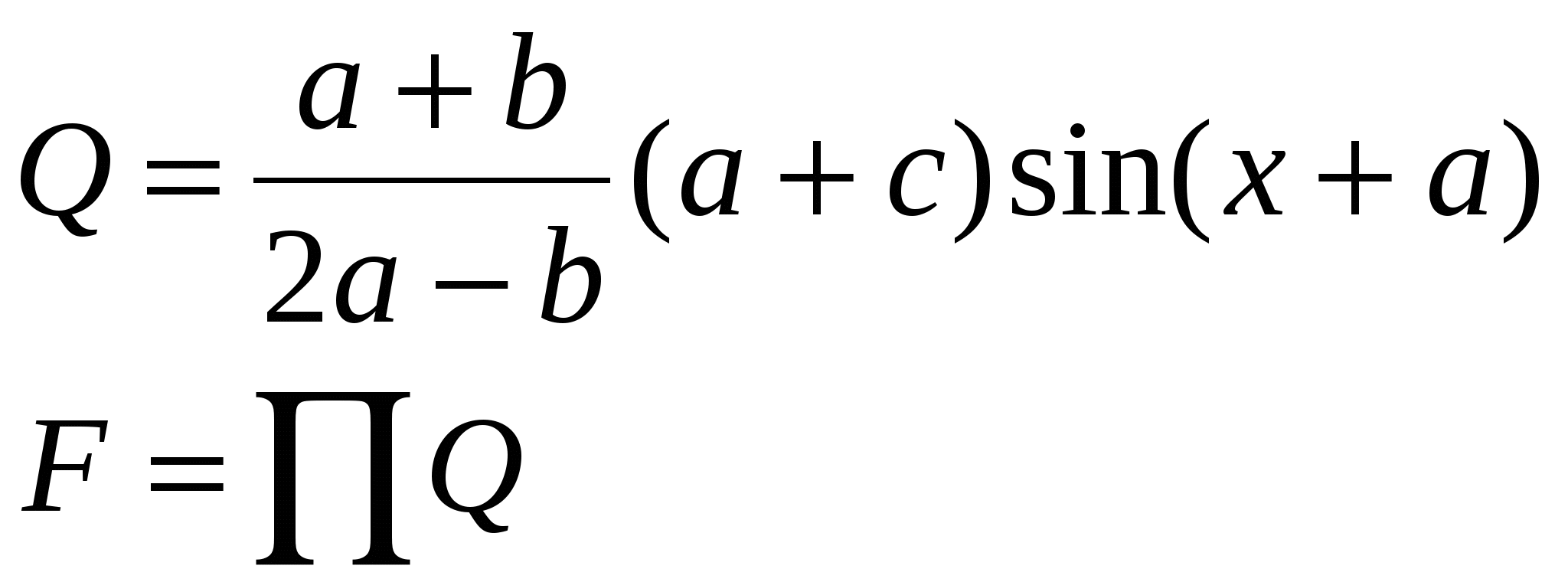
Считать F до тех пор, пока F[-2;5].
|
b, c, x,
a≥0
ha=0.5
|
a, Q, F.
Количество сомножителей в F.
|
11
|
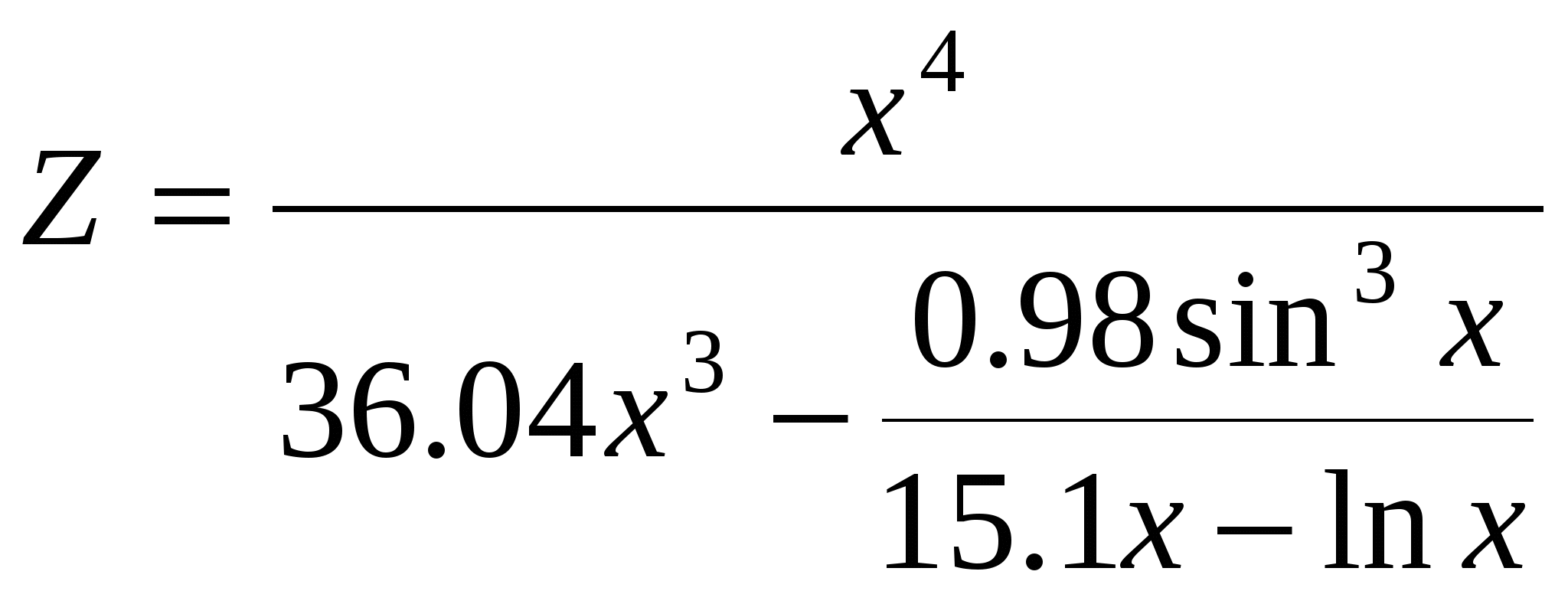
Cчитать Z до тех пор, пока оно остается < Q.
|
Q,
x≥1,
hx=0.1
|
x, Z.
Количество вычисленных Z, и сумма первых пяти Z.
|
12
|
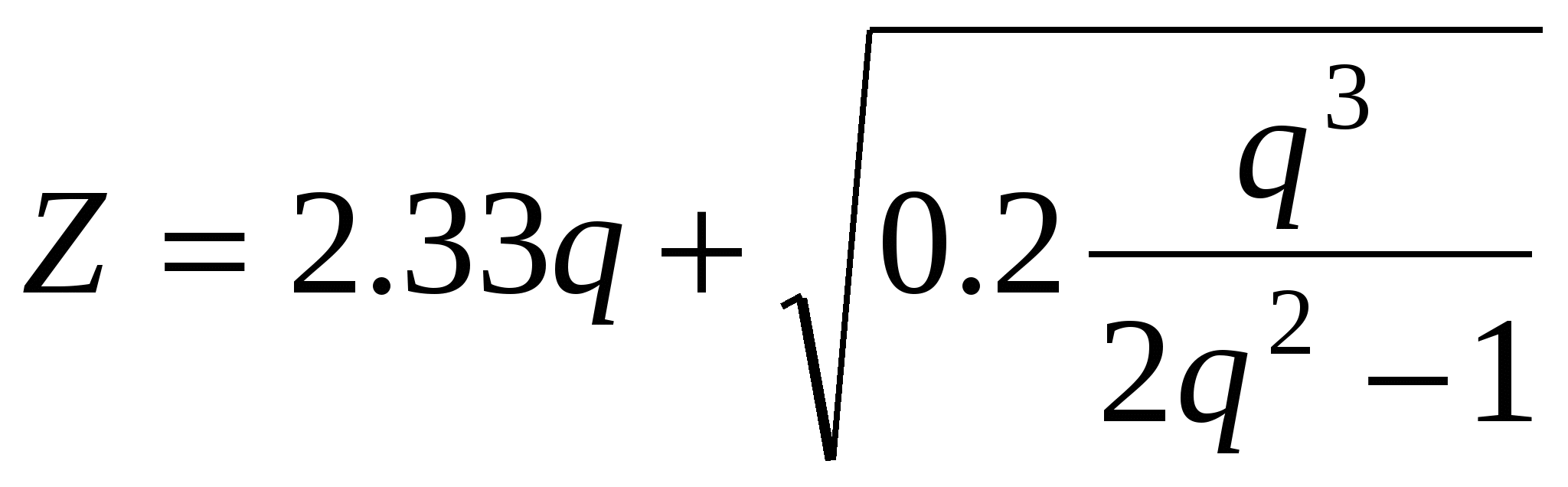
Считать Z до тех пор, пока подкоренное выражение положительно.
|
q ≤ 10
hq=-0.5
|
q, z.
Количество и сумма вычисленных значений Z.
|
13
|
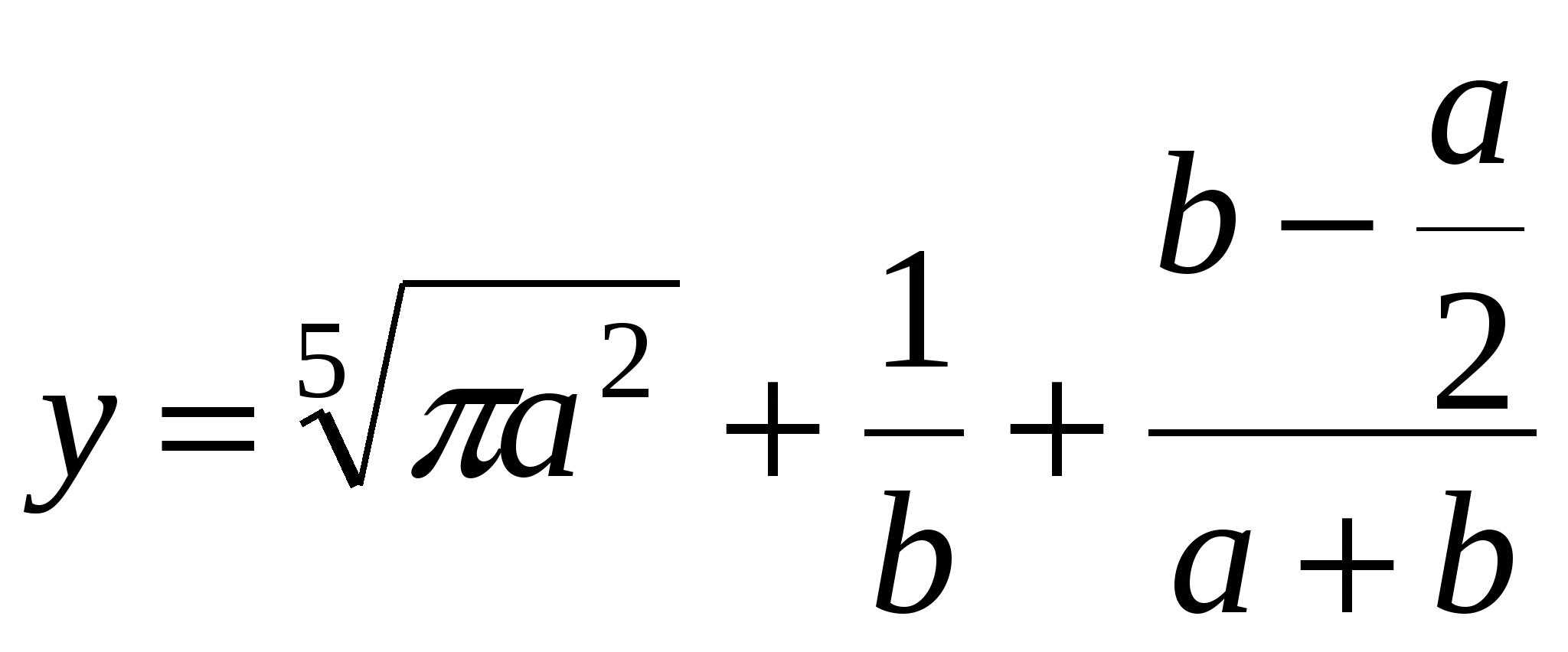
Считать y до тех пор, пока подкоренное выражение ≤ C
|
b, C.
a≥0
ha=0.1
|
a, y.
Вычислить K=N!, где N - кол-во вычисленных y.
|
14
|
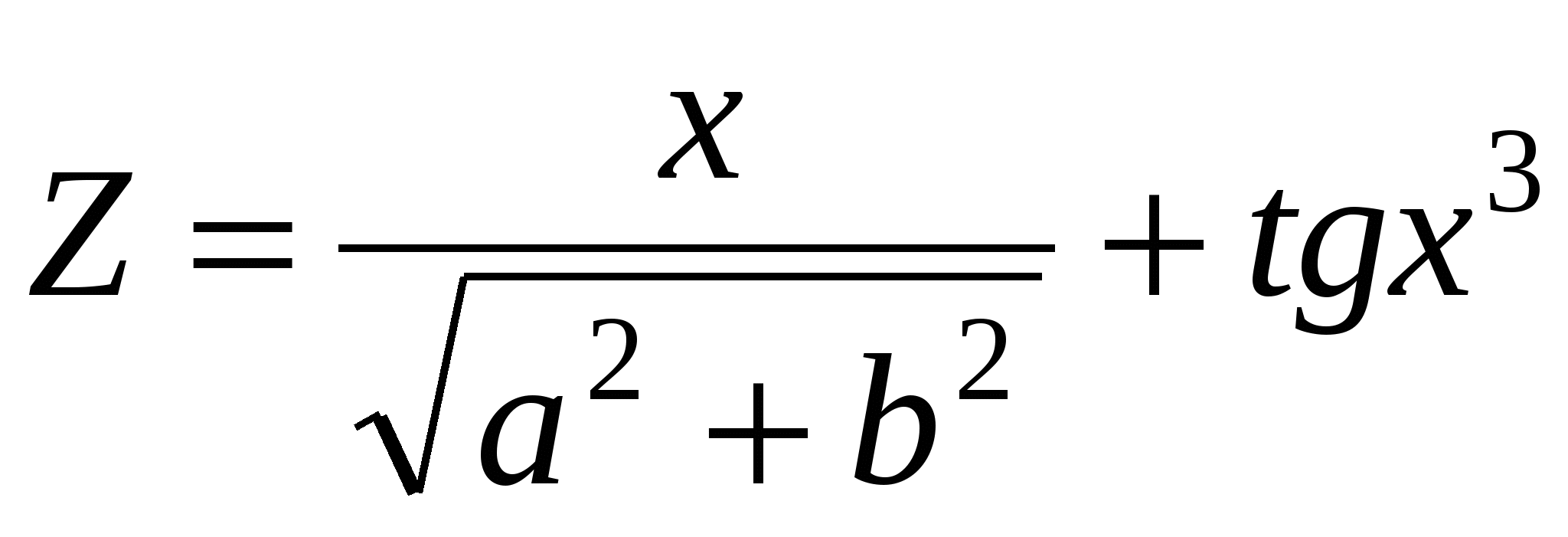 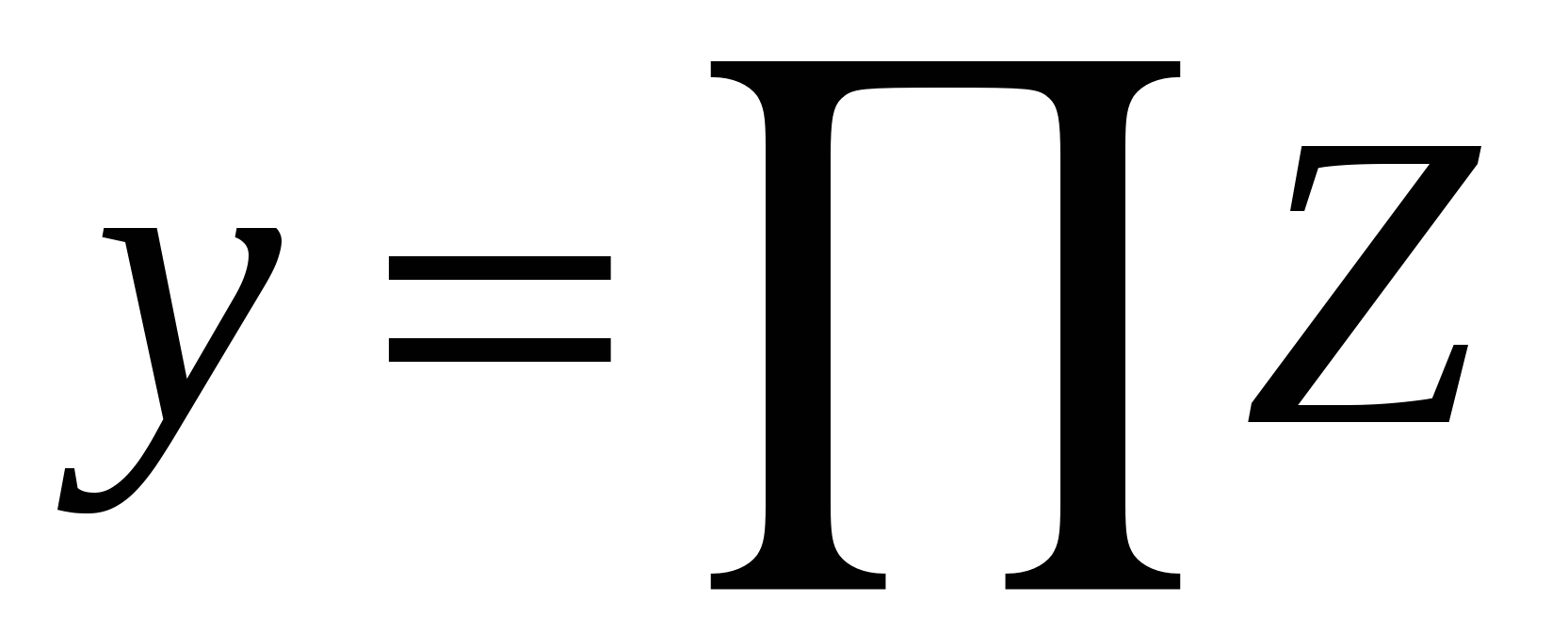 . .
Считать y до тех пор, пока оно остается меньше 100.
|
a, b,
x≥5
hx=0.3
|
Z, x, y.
Количество Z > b.
|
Продолжение таблицы к заданию 3
1
|
2
|
3
|
4
|
15
|
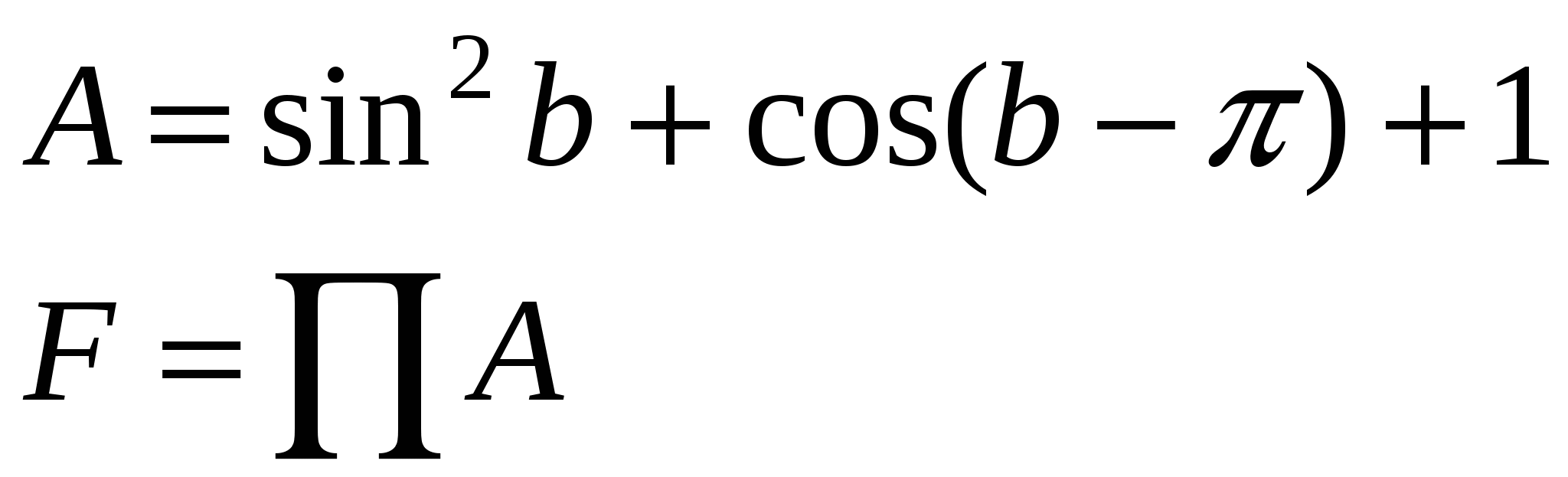
Считать F до тех пор, пока F остается < 10.
|
b≥0
hb=0.1
|
b, A, F.
Количество А > 0.
|
16
|
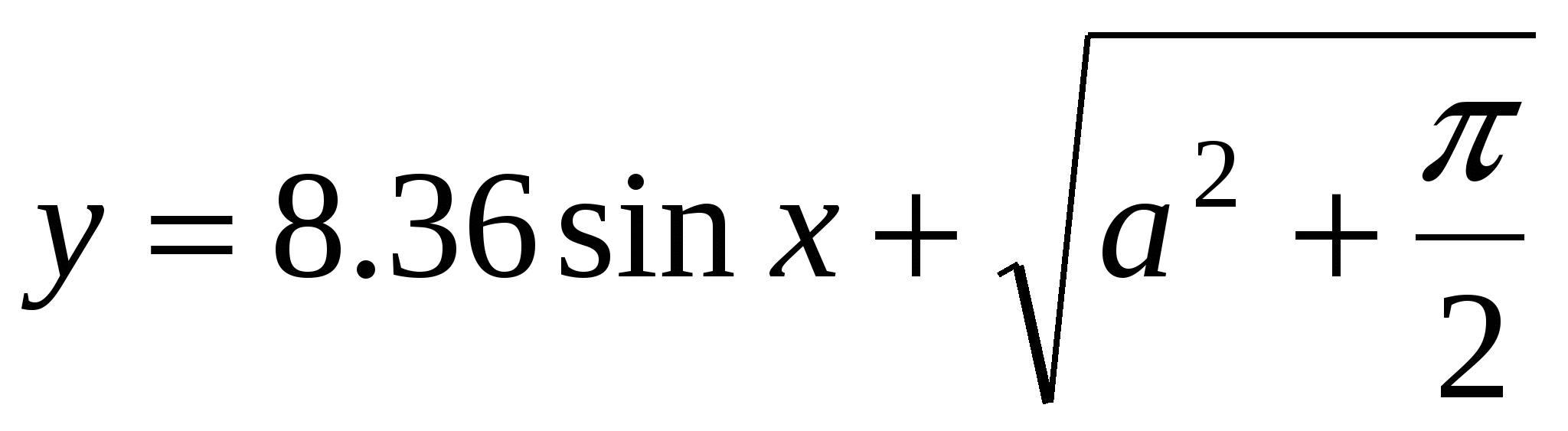 Cчитать y до тех пор, пока Cчитать y до тех пор, пока 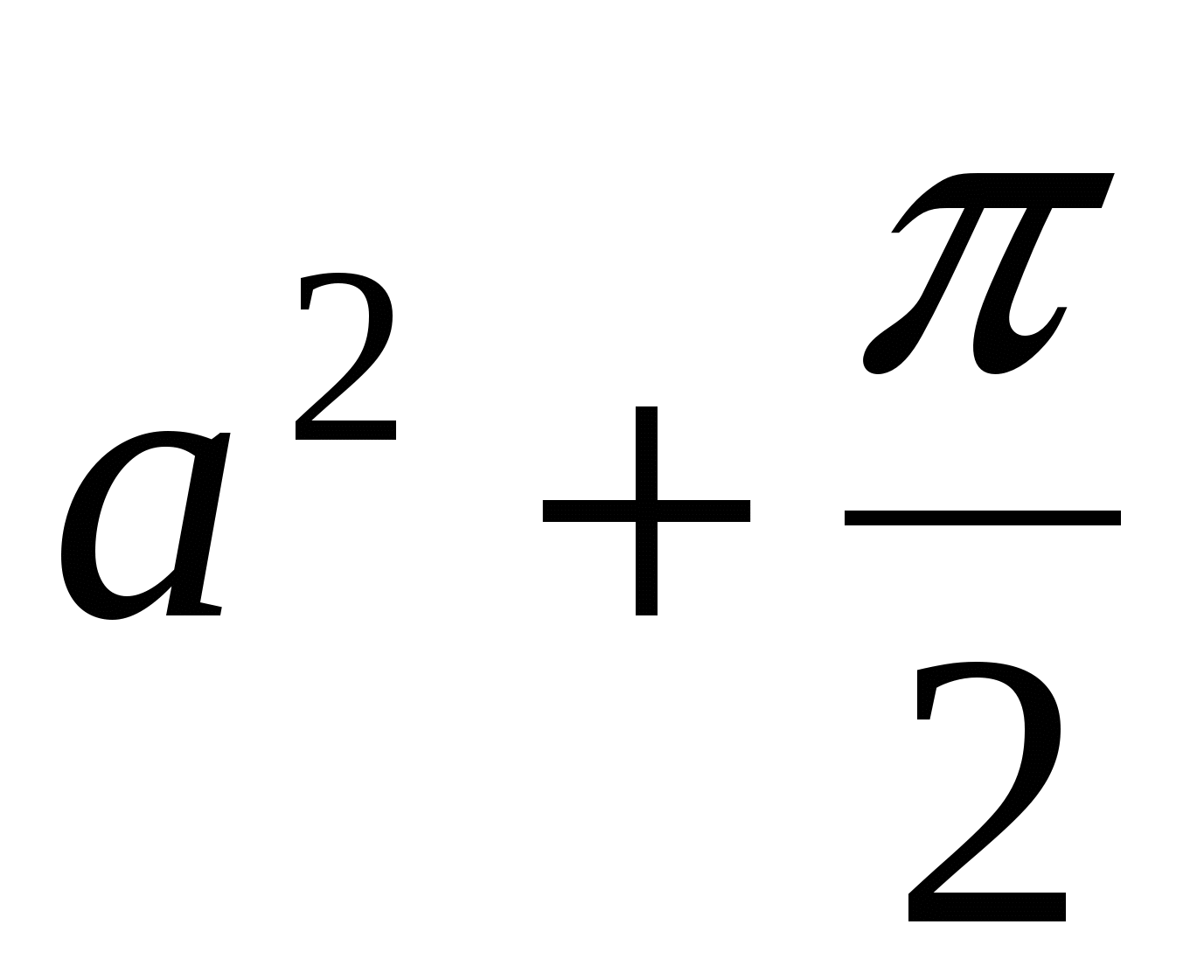 превысит Q. превысит Q.
|
x, Q,
a≥0
ha=0.4
|
a, y.
Количество (N) вычисленных у.
K=N!.
|
17
|
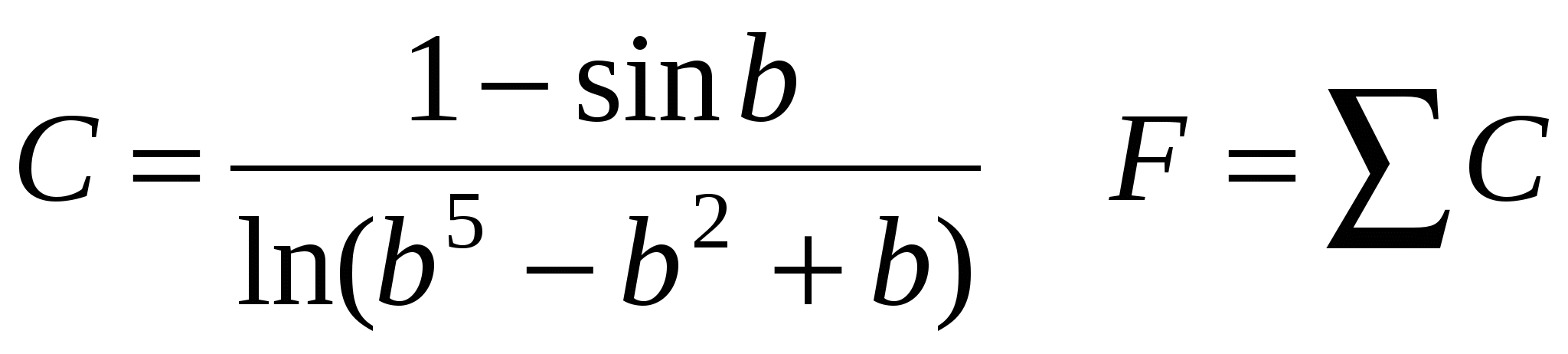
Считать С до тех пор, пока выражение под знаком логарифма >1.
|
b ≤ 3
hb=-0.2
|
b, C, F.
Количество вычисленных С.
|
18
|
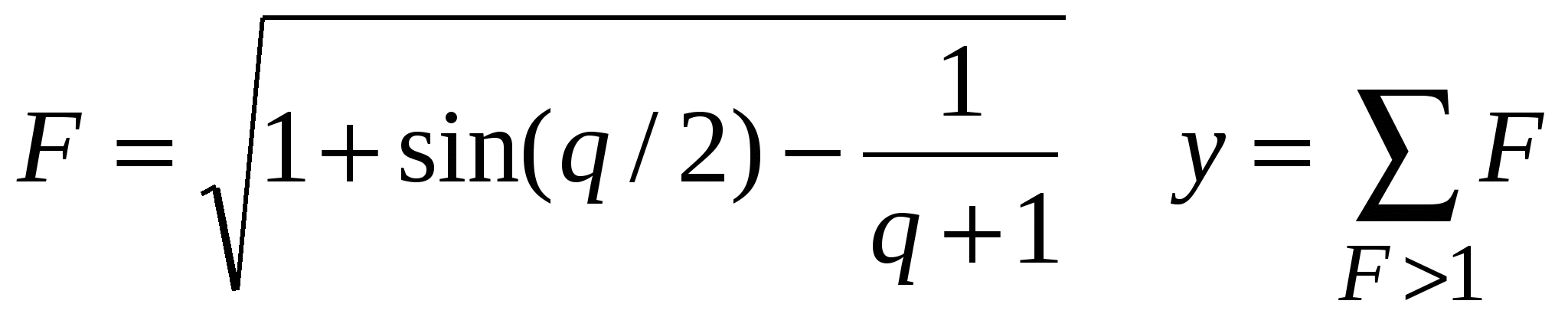
Считать F до тех пор, пока подкоренное выражение >0.
|
q ≤ 2
hq=-0.1
|
F, q.
Количество слагаемых в сумме.
|
19
|
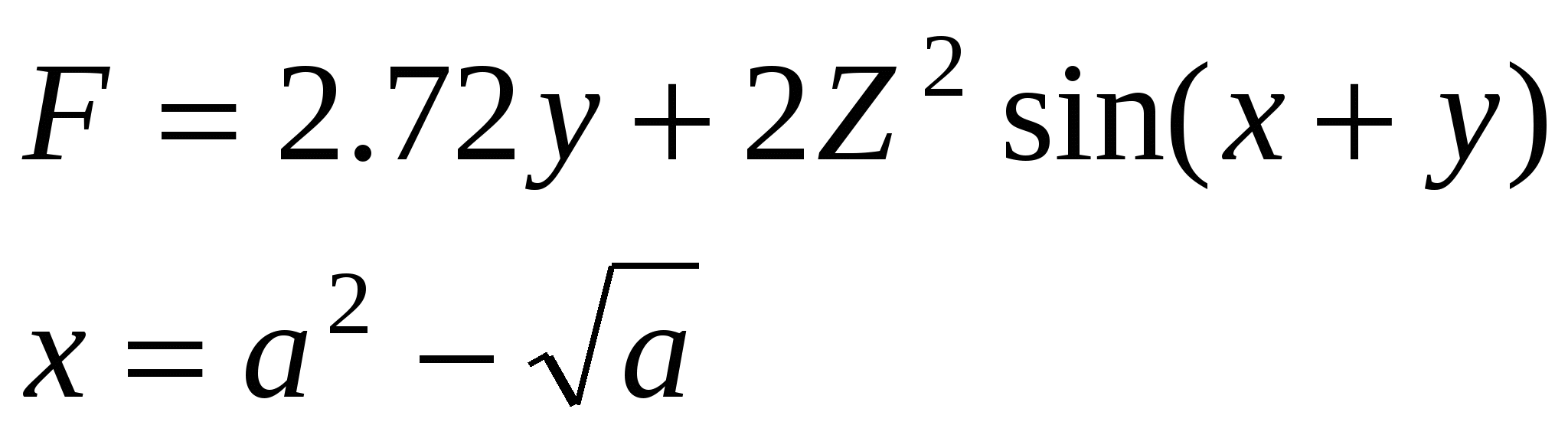
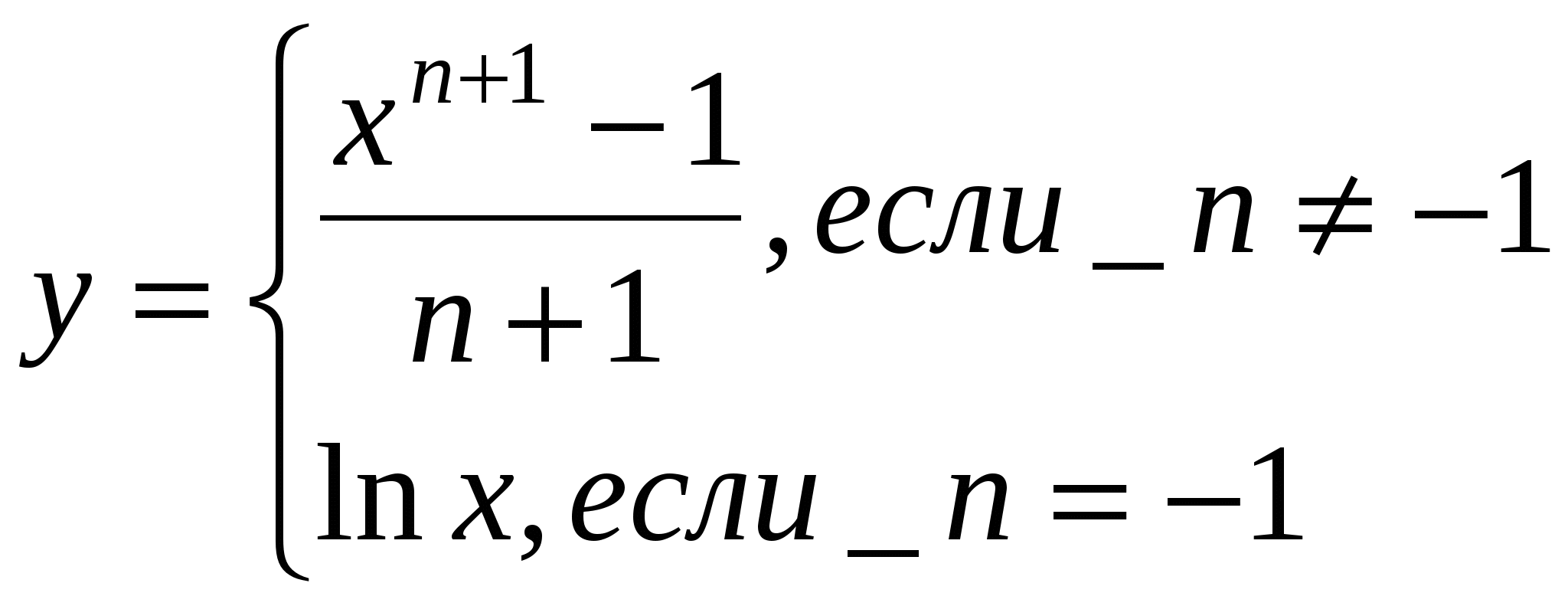
Считать F до тех пор, пока F остаётся меньше 100.
|
a, n
Z ≥0.4
hZ=0.5
|
Z, F, x, y.
Количество вычисленных F.
|
20
|
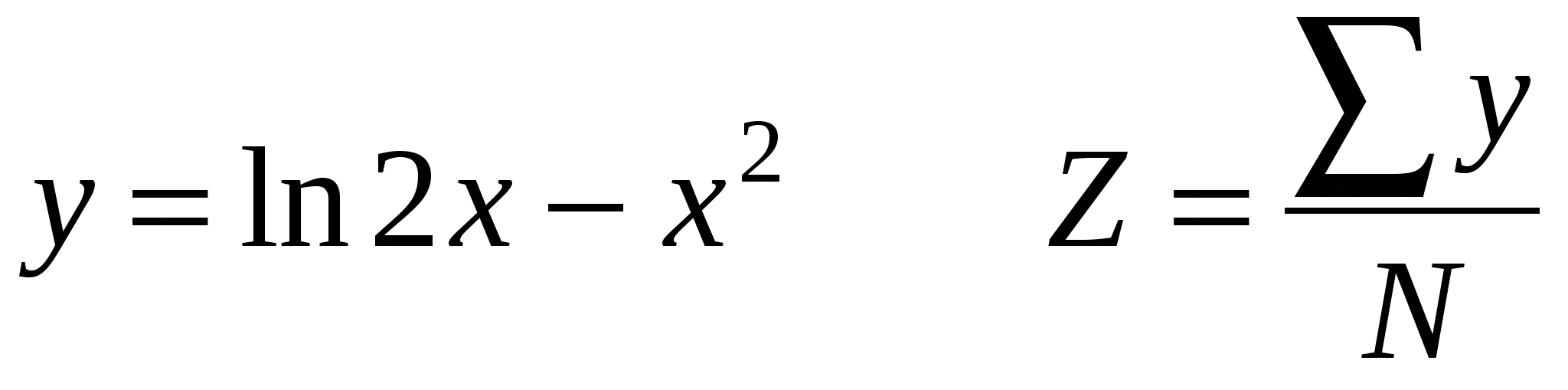
Считать y до тех пор, пока выражение под знаком логарифма >0.
|
x ≤ 10
hx=-0.5
|
x, y, Z.
N – количество слагаемых в сумме.
|
|
 Скачать 1.36 Mb.
Скачать 1.36 Mb.

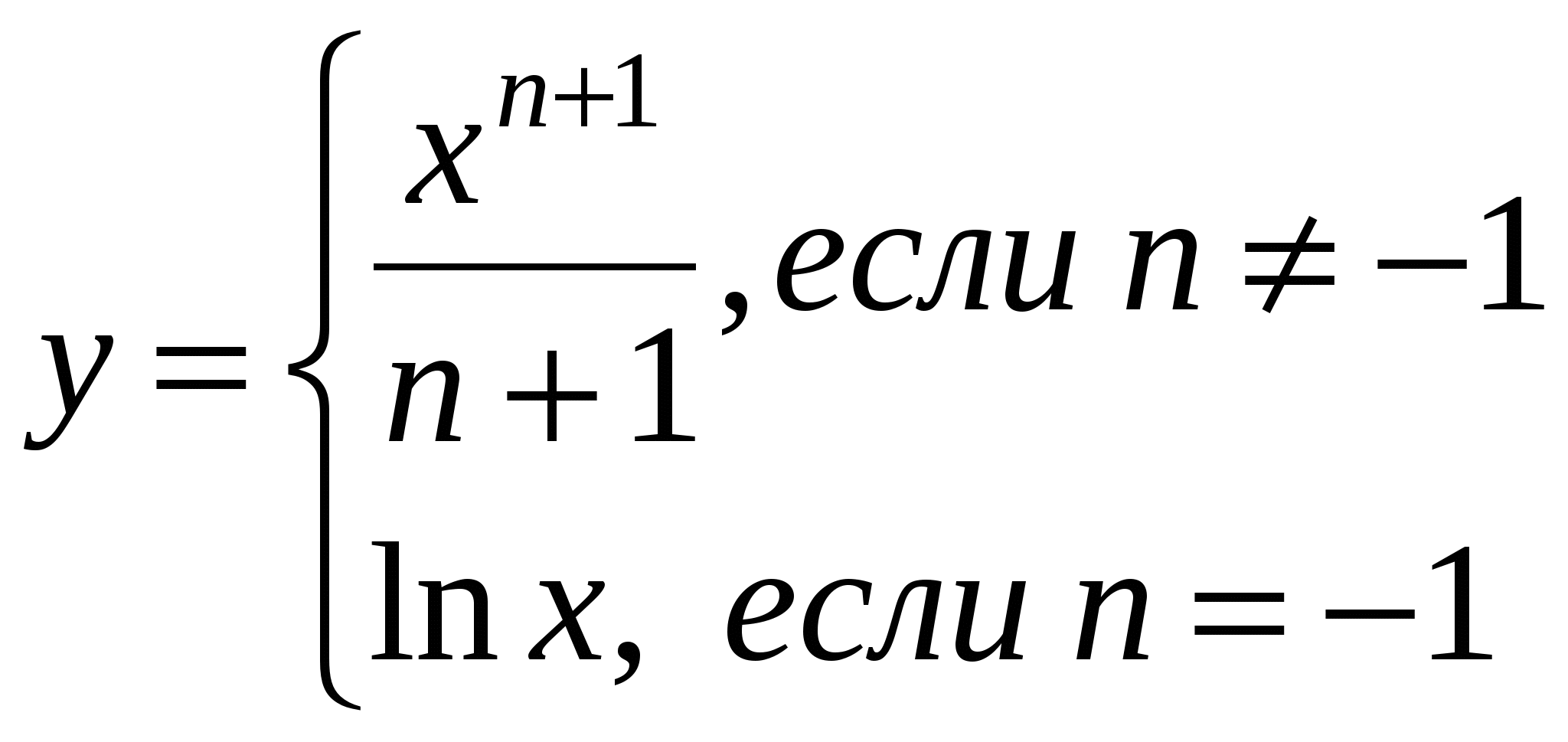 Считать F до тех пор, пока F остаётся меньше 100.
Считать F до тех пор, пока F остаётся меньше 100.