Исполнительные механизмы автоматики. Методическое пособие по исполнительным механизмам. Витебск 2011 оглавление введение
 Скачать 17.4 Mb. Скачать 17.4 Mb.
|
|
Пренебрегая размагничивающим действием реакции якоря, уравнение переходного процесса тахогенератора имеет вид: 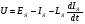 , ,где 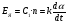 ; LЯ – индуктивность обмотки якоря; ; LЯ – индуктивность обмотки якоря; - угол поворота вала тахогенератора. Если на выходе тахогенератора включён резистор сопротивлением RH, то ток якоря: 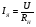 а производная тока: 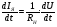 . .Решая совместно все эти уравнения, после несложных преобразований получим: 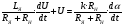 ; или ; или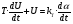 , ,где 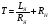 – постоянная времени якорной цепи; – постоянная времени якорной цепи;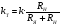 – коэффициент передачи тахогенератора. Изображение по Лапласу полученного уравнения имеет вид: – коэффициент передачи тахогенератора. Изображение по Лапласу полученного уравнения имеет вид:Тр·U(p) + U(p) = k·p·(p) следовательно, передаточная функция тахогенератора: 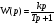 . .Таким образом, если входным параметром является угол поворота вала, то тахогенератор представляет собой реальное дифференцирующее звено. Часто к тахогенератору представляют требования минимальной постоянной времени. Если Т 0, то передаточная функция тахогенератора: W(P)=kp, т.е. тахогенератор является идеальным дифференцирующим звеном. 2.7. Шаговые исполнительные двигатели Шаговые двигатели (ШД) представляют собой многофазные и многополюсные синхронные электрические машины, у которых питание обмоток статора осуществляется импульсным напряжением поочерёдно, с помощью электронного коммутатора. После каждого импульса ротор двигателя поворачивается на определённый угол, называемый шагом. Шаговые двигатели целесообразно применять в тех случаях, когда требуется осуществить прерывистое (стартстопное) движение, а также непрерывное движение, если управляющий сигнал задан в виде серии последовательных импульсов (унитарного кода). В устройствах автоматики наибольшее применение нашли ШД с числом фаз m3, обмотки которых возбуждаются поочередно или группами импульсами напряжения прямоугольной формы. На рис.13 изображена схема ШД с числом фаз m=6. Если подавать поочередно импульсы напряжения на фазные обмотки 1-2-3-4-5-6, то ротор двигателя будет скачком поворачиваться в положение, при котором его ось совпадает с осью фазной обмотки, находящейся под напряжением, т.е., соответственно, 1-2-3-4-5-6. Таким образом, ротор будет иметь шесть устойчивых положений, соответствующих направлению вектора намагничивающей силы F фазной обмотки, включённой в данный момент времени. Шаг двигателя будет при этом равен =360°/m=360°/6= 60°. Можно применить и более сложную схему коммутации фазных обмоток, т.е. подавать напряжение одновременно на несколько фазных обмоток. Так, если одновременно подать напряжения на фазы 1 и 2, то ротор повернётся на угол =360°/(2m)=360°/12=30°. Он установится по оси результирующего вектора намагничивающей силы Fp, равного геометрической сумме векторов F1 и F2. При шаге 30° порядок коммутации фазных обмоток рассматриваемого двигателя может быть различным: вариант А - (1) - (1,2) - (2) - (2,3) - (3) ... ; вариант В - (1,2) - (1,2,3) - (2,3) - (2,3,4). По конструкции ЩД делятся: на магнитоэлектрические, реактивные и индукторные. У магнитоэлектрических ШД ротор выполняется в виде постоянного магнита с одной или несколькими парами полюсов. Статор имеет явно выраженные полюсы, на которые наматываются фазные обмотки. У реактивного ШД ротор выполняется из магнитомягкого материала, а статор имеет m – фазную сосредоточенную обмотку При малом шаге (15) используют реактивный редукторный ШД с гребенчатыми выступами на статоре. Индукторные ШД по конструкции и принципу работы сходны с редукторными двигателями. Управление ШД основано на изменении частоты, числа и порядка подачи импульсов постоянного напряжения в фазные обмотки. Изменением частоты импульсов регулируют частоту вращения ШД. Поворот выходного вала ШД на заданный угол осуществляется подачей определённого числа импульсов. Перемена направления вращения выходного вала ШД осуществляется изменением порядка подачи импульсов на фазные обмотки от электронного коммутатора. Выбирая в качестве исполнительного двигателя шаговый двигатель, необходимо учитывать ряд его особенностей: 1. Положение ротора ШД в статическом режиме устойчивое, т.к. существует синхронизирующий момент, фиксирующий положение ротора по отношению к статору. У двигателей постоянного и переменного тока такого момента нет. 2. ШД может обеспечить широкий диапазон регулирования частоты вращения от максимального до нуля. 3. Движение ротора ШД дискретное с шагом от 1,5° до 36° в зависимости от типа ШД и выбранного числа тактов коммутации фазных обмоток. 4. Скорость изменения частоты управляющих импульсов не должна быть больше определённого для каждого типа ШД значения, называемого частотой приёмистости. Частота приёмистости для серийно выпускаемых ШД может быть в диапазоне от 100 Гц до 2500 Гц. Технические характеристики некоторых шаговых двигателей приведены в таблице 2.11. Таблица 2.11
2.8. Выбор типа исполнительного механизма и редуктора. Проектирование исполнительной части автоматических систем состоит из следующих этапов: выбор типа исполнительного электродвигателя, предварительного выбора параметров механической передачи, определение мощности исполнительного электродвигателя и уточнение параметров редуктора. В системах мощностью до 7580 Вт целесообразно применение двухфазных асинхронных двигателей. В более мощных системах применяются электродвигатели постоянного тока. При выборе двигателя необходимо учитывать такой фактор как перегрузочная способность – способность кратковременно развивать максимальный момент. В реальных условиях эксплуатации нагрузка на валу двигателя колеблется в достаточно широких пределах. Для лучшего использования его номинальный момент выбирают из соотношения: МН = (1,01,8)МС, где МС – среднее значение нагрузки; Мн – номинальный крутящий момент двигателя. Проверка двигателя на нагрузку производится из условия: Мmax Мн, где – коэффициент допустимой нагрузки. Передаточная способность электродвигателей постоянного тока =(34) несколько выше, чем у асинхронных двухфазных электродвигателей <3, поэтому двигатели постоянного тока предпочтительнее в условиях резких изменений момента нагрузки. При выборе редуктора необходимо обращать внимание на такие характеристики, как КПД, люфт, инерционность. КПД редуктора влияет на диапазон плавных скоростей электродвигателя. При меньшем КПД диапазон сужается, расширяется зона нечувствительности. К сведению: цилиндрическая зубчатая пара имеет КПД 0,90,94, коническая – 0,880,92, червячная пара 0,50,7, планетарной передачи – 0,80,95. Применение червячных пар не рекомендуется не только из-за низкого КПД, но и из-за возможности заклинивания. Люфт передачи должен быть минимальным, т.к. может стать причиной автоколебаний. Для уменьшения люфта, когда это необходимо, применяют разрезные шестерни прямозубые и косозубые. Инерционность редуктора в значительной степени определяется рациональностью распределения передаточных отношений между его ступенями. Замена стальных шестерен пластмассовыми позволяет уменьшить момент инерции на 40-60 %. При выборе исполнительного двигателя исходными данными служат: Мс – статический момент нагрузки; wmax – максимальная угловая скорость нагрузки; Еmах – максимальное угловое ускорение нагрузки; Jm – момент инерции исполнительного механизма. Мощность, развиваемая двигателем, должна быть достаточной, чтобы обеспечить на нагрузке требуемый момент, скорость и ускорение. Поскольку исполнительный электродвигатель связан с нагрузкой через редуктор, то следует привести её к валу двигателя. Приведённый момент инерции нагрузки: 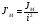 (2.30) (2.30)где 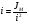 – передаточное отношение редуктора; – передаточное отношение редуктора;Jм – момент инерции нагрузки; – скорость вращения вала двигателя; н – скорость вращения выходного вала редуктора. Полный момент инерции равен: 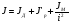 (2.31) (2.31)где JД – момент инерции ротора двигателя; J'P – приведенный момент инерции редуктора. Динамический момент на валу двигателя: МД = J·i·max С учётом КПД редуктора: 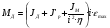 . (2.32) . (2.32)Общий момент на валу должен быть равен сумме моментов динамического и статического: 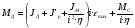 . (2.33) . (2.33)Анализ этого выражения показывает, что требуемый от двигателя момент может быть сведён к выбору оптимального для этой цели передаточного отношения. Продифференцируем по i выражение (2.33) и приравняем результат к нулю: 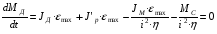 . .Отсюда находится оптимальное передаточное отношение: 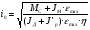 . (2.34) . (2.34)Подставив i0 в уравнение (2.33) и умножив на , можно получить требуемую мощность двигателя: 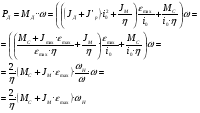 Окончательно: 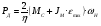 (2.35) (2.35)Двигатель выбирается либо мощностью Рд по выражению (2.35), либо несколько большей. Далее осуществляется проверка: - определяется оптимальное передаточное отношение; - проверяется требуемая мощность двигателя по формуле: 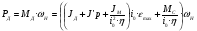 . .Двигатель, выбранный таким образом, проверяется по моменту и по скорости, исходя из условий: 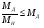 ; ; 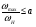 , где a 1,2 1,3 , где a 1,2 1,3Изложенная методика рекомендуется при выборе двигателя постоянного тока. Пример. Выбрать исполнительный двигатель для следящей системы по следующим данным: МС =14 Н·м; JM = 1,5 кг·м2; Н = 18 об/мин.= 1,88 рад/с; m = 2 рад/с . Определяем требуемую мощность исполнительного двигателя, задавшись КПД редуктора = 0,8. 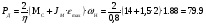 (Вт). (Вт).По техническим данным (табл.2.5) выбираем двигатель СЛ–521 с параметрами: Рн = 77 Вт; nН = 3000 об/мин; UH = 110В; МН =250·10-3 Н·м; Мкр = 650·10-3 Н·м; м = Мкр/МН = 2,6; JД = 17·10-5 кг·м2. Определим оптимальное по моменту передаточное число редуктора, приняв J'P=0,2·JД 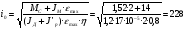 . .Вычисляем требуемый максимальный момент 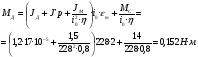 Проверяем перегрузку двигателя по моменту и скорости 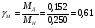 ; ; 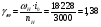 . .Двигатель оказался перегружен по скорости, но недогружен по моменту, поэтому нужно уменьшить передаточное число редуктора. Определим передаточное число редуктора, обеспечивающего максимальную скорость нагрузки 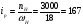 . .Пересчитаем максимальный требуемый момент 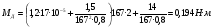 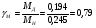 ; ; 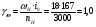 . .При выборе двухфазного асинхронного двигателя необходимо руководствоваться следующими соображениями: - скорость вращения однофазного двигателя определяется частотой напряжения питания, поэтому передаточное отношение находится в соответствии с заданной скоростью вращения нагрузки; - в ориентировочных расчётах моментом нагрузки можно пренебречь; - момент инерции редуктора оказывается преобладающим по сравнению с моментом инерции ротора (для двигателей с полым ротором) и нагрузки; - основное требование, предъявляемое к электродвигателю – обеспечение коэффициента динамических свойств (отношение 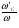 ). Исходным является уравнение динамики привода: ). Исходным является уравнение динамики привода: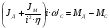 (2.36) (2.36)где JД = Jр.Д + J'p – суммарный момент инерции ротора электродвигателя и приведенного момента инерции редуктора; Мс – приведенный к валу двигателя суммарный момент нагрузки и редуктора 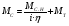 ; ;Мс.н – статический момент нагрузки; Мт – момент трения в редукторе; Мд – вращающий момент двигателя, равный пусковому Мп. Подставив в формулу (2.36) значение передаточного отношения, получим: 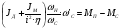 . .Это уравнение можно привести к виду: 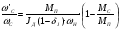 , (2.37) , (2.37)где 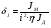 – относительный момент инерции нагрузки. – относительный момент инерции нагрузки.Для выбора исполнительного электродвигателя переменного тока необходимо: 1. Вычислить требуемый коэффициент динамических свойств. 2. Определить передаточное отношение редуктора и КПД 3. Вычислить момент инерции редуктора, приведенный к валу двигателя. 4. Определить момент инерции нагрузки, принимая равным нулю момент инерции ротора электродвигателя. 5. Найти приведенный статический момент нагрузки и редуктора. 6. Выбрать двигатель, у которого номинальный вращающий момент не менее Мс. 7. Из числа выбранных взять тот, у которого при проверке по (2.37) коэффициент динамических свойств оказался равным либо большим по сравнению с требуемым. 2.9. Электромагнитные силовые элементы Исполнительные элементы с электромагнитными силовыми механизмами являются наиболее простыми, надёжными и быстродействующими. Они находят применение для управления стандартными устройствами, для перемещения регулирующих органов на небольшое расстояние, в цифропечатающих устройствах и т.п. Далее для краткости будем их называть "электромагниты". Если подключить обмотку электромагнита с фиксированным зазором к источнику постоянного тока, то изменение тока в обмотке будет определяться следующим соотношением: 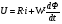 . (2.38) . (2.38)Умножив (2 38) на i·dt и проинтегрировав за время t, в течение которого магнитный поток возрастает от 0 до Ф, получим: 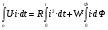 . (2.39) . (2.39)Левая часть представляет собой электрическую энергию, полученную от источника, первое слагаемое правой части -электрическую энергию, перешедшую в тепловую, и второе –энергию магнитного поля. Пренебрегая потерями в магнитопроводе можно считать всю магнитную энергию сосредоточенной в воздушном зазоре. Величина магнитной энергии определяется: 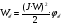 , ,где 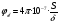 – магнитная проводимость плоско -параллельного воздушного зазора. – магнитная проводимость плоско -параллельного воздушного зазора.Магнитная энергия затрачивается на совершение работы по перемещению якоря электромагнита под действием тяговой силы Рэ, которая определяется: 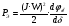 . (2.40) . (2.40)С учётом значений магнитной проводимости окончательно получим выражение для тяговой силы электромагнита 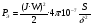 . (2.41) . (2.41)2. 10. Особенности расчётов электромагнитов переменного тока Поскольку основным источником питания систем промышленной автоматики является сеть переменного тока, то в связи с этим электромагнитные устройства переменного тока получили достаточно широкое распространение. Из выражения (2.41) видно, что тяговое усилие пропорционально квадрату тока и, следовательно, при изменении направления тока своего знака не меняет. Для уменьшения потерь на вихревые токи и гистерезис, причиной которых является переменный магнитный поток, магнитопровод выполняют шихтованным из листов электротехнической стали. Для электромагнитов переменного тока характерна вибрация якоря. Причина этого станет ясной из анализа выражения 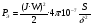 , ,здесь i = Jmax · sint; 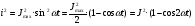 . .Подставляя действующее значение тока в исходное выражение, получим: 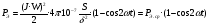 , ,Таким образом, тяговая сила электромагнита переменного тока меняется с частотой, вдвое превышающей частоту питания. Это вызывает вибрацию якоря, которая приводит к повышенному износу подвижных частей. Для исключения этого явления электромагнит выполняют двух обмоточным, сдвиг фаз питания обеспечивается подключением к обмоткам индуктивности и ёмкости (рис.14а), либо введением короткозамкнутого витка, который одевается на сердечник (рис.146). а) б) В результате таких мер в магнитной системе появляются два пульсирующих магнитных потока, сдвинутых во времени так, что в любой момент на якорь действует сила, отличная от нуля. Тяговая характеристика электромагнита переменного тока зависит от способа его включения и это является ещё одной особенностью этих электромагнитов. Рассмотрим первый способ, характерный для электромагнитных реле. Обмотка включается последовательно с электрическими устройствами с большим сопротивлением. Ток в такой цепи не зависит от положения якоря, и выражение для тяговой силы электромагнита остаётся в том же виде, что и для электромагнита постоянного тока с плоскими наконечниками: 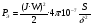 . .Второй случай характерен для силовых электромагнитов. В этом случае обмотки включены непосредственно в сеть, напряжение которой можно считать постоянным, независящим от положения якоря. Для этих условий: 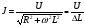 , считая XL >> R. , считая XL >> R.Индуктивность магнита равна: 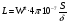 . .Отсюда ток в обмотке электромагнита: 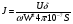 . .Подставив значение тока в выражение для тяговой силы получим: 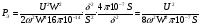 . .Из этого выражения видно, что тяговая сила при U = const от величины зазора не зависит. 2.11. Расчет обмоток электромагнита постоянного тока Укладка обмотки в катушке электромагнита может быть шахматной, шаговой и в навал. В первом случае плотность укладки привода будет наибольшей, в последнем – наименьшей. Плотность укладки определяется величиной коэффициента неплотности КН. Число витков на единицу площади обмоточного окна находится по формуле: 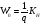 , ,где q – площадь поперечного сечения обмоточного провода. Отсюда число витков в катушке электромагнита: 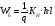 , (2.43) , (2.43)где h и l – соответственно, высота и длина обмоточного окна. Ток питания обмоток определяется известным соотношением: |
