Исполнительные механизмы автоматики. Методическое пособие по исполнительным механизмам. Витебск 2011 оглавление введение
 Скачать 17.4 Mb. Скачать 17.4 Mb.
|
|
J=q·j, (2.44) где j – плотность тока. Для электромагнитов, работающих в длительном режиме рекомендуемая плотность тока в медном проводе – 3 А/мм2, при повторно-кратковременном режиме 5 А/мм2 и при кратковременном 12 А/мм2. Из (2.43) и (2.44) можно получить выражение для намагничивающей силы JW = j·KH·h·l. (2.45) Как видно из этого выражения, размеры обмоточного окна однозначно, с учётом коэффициента неплотности и плотности тока, определяют намагничивающую силу обмотки электромагнита. Электрическое сопротивление обмотки составляет: 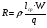 , ,где lcр – длина среднего витка, – удельное сопротивление материала обмоточного провода. Напряжение питания: 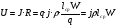 . .На завершающей стадии расчёта определяется максимальная температура нагрева обмоток электромагнита. Температура нагрева зависит от соотношения между потребляемой мощностью и поверхностью. При нормальных условиях на 1 Вт потребляемой мощности должно приходиться (814) 10-4 м2. Пример расчёта тягового электромагнита постоянного тока. Задано: тяговая сила РЭ = 100 н; ход якоря = 10 мм; площадь якорного наконечника S =4 см2; ток питания J = 2А. 1. В соответствии с формулой (2.41) число витков обмотки катушки электромагнита 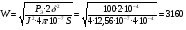 . .2. Найдём диаметр обмоточного провода при условии длительного режима работы ( j = 3 А/мм2) 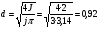 . .Выбираем из ряда стандартных диаметров d = 0,92. 3. Определим размеры катушки электромагнита, приняв КН = 0,7, для этого: а) найдём площадь обмоточного окна 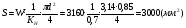 , ,б) выберем следующие размеры обмоточного окна: h =30 мм, l = 100 мм, отсюда размеры катушки: d = 24 мм, D = 84 мм, l = 74 мм. 4. Найдём длину l и сопротивление обмоточного провода: длина среднего витка составляет: 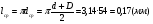 , ,отсюда 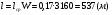 , ,сопротивление провода 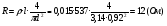 . .5. Вычислим напряжение питания электромагнита: U = J·R = 2 12 = 24 (B). Электромагнит, соответствующий расчётам, изображён на рис.15. Технические данные некоторых электромагнитов постоянного и переменного тока приведены, соответственно, в табл.2.12 и 2.13. Таблица 2.12
Таблица 2.13
2.12. Электромагнитные муфты В современной технике в различного рода системах автоматического управления используются электромагнитные муфты. Широкая область применения муфт привела к большому разнообразию их видов и конструкций. По характеру связи между входными и выходными элементами муфты можно разбить на следующие группы:
На рис.16 изображена однодисковая фрикционная муфта с электромагнитным управлением. Двигатель привода 1 непрерывно вращает ведущий вал с диском 2. При вымоченном состоянии движение на ведомый диск 3 не передаётся, так как якорь 5 электромагнита за счёт возвратной пружины 4 находится в правом положении и межу дисками 2 и 3 существует воздушный зазор. При включении муфты ток, протекающий по обмотке электромагнита 6, создаёт магнитное поле и электромагнитную силу F , втягивающую якорь внутрь обмотки. Ведомый диск с валом прижимается к ведущему диску и начинает вращаться, передавая движение на объект управления 7. Однодисковая муфта проста по устройству, но малоэффективна и практически нерегулируема по крутящему моменту. Этот недостаток в значительно степени снижен в многодисковых муфтах. Крутящий момент, передаваемый муфтой вычисляется по формуле: 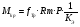 (2.41) (2.41)где fTp – коэффициент трения; R – средний радиус поверхности трения; m – число пар поверхностей трения; Р – сила притяжения якоря муфты; КЭ – коэффициент запаса по крутящему моменту. Сила притяжения определяется из соотношения: 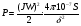 , (2.42) , (2.42)где J – ток в обмотке управления; W – число витков обмотки управления; S – сечение магнитопровода; – величина зазора. Переходной процесс при включении муфты можно разбить на три этапа. Первый этап начинается с момента включения муфты и заканчивается достижением якорем положения, при котором зазор между дисками оказывается равным нулю. Этот этап описывается следующей системой уравнений: 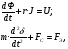 (2.43) (2.43)где U – напряжение питания; r – сопротивление обмотки управления; m – масса подвижных частей; Fc – сопротивление движению диска; FЭ – тяговая сила. Второй этап начинается с момента соприкосновения поверхностей трения и заканчивается полным сцеплением. В течение этого этапа поверхности трения проскальзывают, а скорость ведущего вала уменьшается до тех пор, пока не сравняется со скоростью ведомого. Система уравнений, описывающих этот этап: 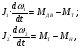 (2.44) (2.44)здесь J1 и J2 – моменты инерции, соответственно, ведущей и ведомой частей; Мдв – момент развиваемый двигателем; Мт -момент трения; МН - момент нагрузки; 1, 2 – скорости вращения ведущей и ведомой частей. Третий этап начинается после полного сцепления муфты и заканчивается разгоном всех вращающихся частей до номинальной скорости вращения. Этот этап описывается уравнением: 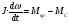 , ,где J – полный момент инерции вращающихся частей; Мкр – крутящий момент; Мс - момент сопротивления. Муфта с электромеханической связью (ферропорошковая) изображена на рис.17. Пространство между полумуфтами 1 и 2 заполнено ферромагнитной средой 3, состоящей из смеси кремнистого железа и смазывающего вещества (тальк, графит), улучшающего проскальзывание полумуфт при холостом ходе. При подаче тока в обмотку 4 ведущей полумуфты 1 возникающее магнитное поле намагничивает отдельные частички железа, которые слипаются между собой, и вязкость среды 3 увеличивается. Ведомая полумуфта начинает вращаться. По мере увеличения тока в обмотке увеличивается сила вязкого трения и значение момента передаваемого на ведомый диск. Таким образом, фрикционные муфты с вязким трением являются управляемыми, позволяющими плавно регулировать передаваемый вращающий момент, а следовательно и частоту вращения ведомого вала. Крутящий момент, развиваемый муфтой, определяется: 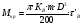 (2.45) (2.45)здесь 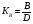 – отношение ширины сцепляющего слоя к среднему диаметру этого слоя; – отношение ширины сцепляющего слоя к среднему диаметру этого слоя;'В = Кр·В – удельная сила сцепления, в которой принимают Кр=0,70,8; В = (0,20,4) 105; m –масса подвижных частей. Величина·В является исходной при расчёте обмоток управления и параметров магнитной цепи. Динамические свойства муфты находятся из анализа дифференциальных уравнений электрической цепи и моментов: 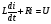 , (2.46) , (2.46)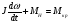 , (2.47) , (2.47)где L – индуктивность обмотки управления; R – активное сопротивление обмотки; Мн = z · – момент нагрузки, приведённый к ведомому валу; z – коэффициент вязкого трения; Мкр= с · i – крутящий момент. Уравнение (2.47) может быть записано в виде: 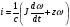 , ,подставив полученное таким образом значение i в (2.46), получаем уравнение нагруженной муфты: 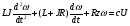 , (2.48) , (2.48)и ненагруженной: 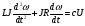 (2.49) (2.49)Разделив уравнение (2.48) нагруженной муфты на Rz и подставив: 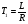 – электрическая постоянная времени; – электрическая постоянная времени;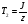 – механическая постоянная времени; – механическая постоянная времени;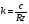 – коэффициент передачи, – коэффициент передачи,придём к виду: 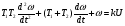 . .Отсюда передаточная функция нагруженной муфты: 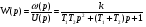 . (2.50) . (2.50)Разделив уравнение ненагруженной муфты на JR после соответствующей подстановки, получим: 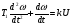 , , 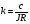 . .Отсюда передаточная функция ненагруженной муфты: 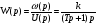 . (2.51) . (2.51)Муфта со связью через поле (асинхронная индукционная) изображена на рис.18. Ведущий вал 4 вращает индуктор, состоящий из магнитопровода 3 и катушки возбуждения 2. К индуктору через щётки 6 и контактные кольца 5 подводится во время работы постоянное напряжение. Возникающий магнитный поток замыкается через воздушный зазор и якорь 1. В результате взаимодействия токов, возникающих в якоре при вращении индуктора, и создаваемого его обмоткой 2 магнитного потока, возникает вращающий момент. Якорь начинает вращаться вслед за индуктором и вращать ведомый вал. По принципу действия этой муфты необходимо, чтобы якорь вращался несколько медленнее, чем индуктор, так как в противном случае в якоре не будут индуцироваться токи и исчезнет вращающий момент. Технические данные электромагнитных фрикционных муфт (МЭС), порошковых (МПБ), гистерезисных (НГБ), торможения (МЭТ) приведены в таблице 2.14. Таблица 2.14
|
