Исполнительные механизмы автоматики. Методическое пособие по исполнительным механизмам. Витебск 2011 оглавление введение
 Скачать 17.4 Mb.
|
|
Р = Р·FЭФ·- РТР = (Р2 – Р1)·FЭФ – FТР; б) для исполнительных механизмов с пружинами Р = (Р2 – Р1)·FЭФ·- РТР РПР, где FЭФ – эффективная площадь мембраны; (Р2 – P1) – разность давлений по обе стороны мембраны (для исполнительных механизмов с пружинами; Р1 – атмосферное давление); Ртр – сумма сил сопротивления движению вследствие трения в механизме; РПР = с · h - сила сопротивления пружины. Для среднего положения мембраны (когда все точки мембраны лежат в одной плоскости) их эффективные площади могут быть определены: для мембран с жёстким центром 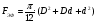 ;для мембран без жёсткого центра 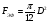 .Как видно, при одинаковых диаметрах FЭФмембран с жёстким центром получаются значительно большие, чем у мембран без жёсткого центра. Поэтому при одних и тех же развиваемых тяговых усилиях, исполнительные механизмы с мембранами с жёстким центром имеют меньшие габариты и вес, чем исполнительные механизмы с мембранами без жёсткого центра. Постоянная времени для пневматических мембранных исполнительных механизмов определяется: 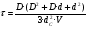 ,где dC – диаметр сечения подводящего трубопровода; V – скорость движения сжатого воздуха.  Рис.34.В последнее время в некоторых системах автоматизации начинают применяться сильфонные исполнительные механизмы. Эти механизмы перспективны в тех случаях, когда для управления приводным механизмом требуется небольшое перестановочное усилие при небольшом ходе ведущего звена. В сильфонном исполнительном механизме силовым элементом является гофрированная трубка–сильфон. На рис.34 приведены типовые схемы сильфонных исполнительных механизмов с подачей давления во внутреннюю (рис.34.а) и наружную (рис.34.б) полость сильфона. Преимущества сильфонных ИМ заключаются в небольших габаритах, простоте конструкции, обладают высоким быстродействием и постоянством развиваемого усилия на выходном штоке вследствие неизменности эффективной площади сильфона. Усилие, развиваемое сильфонным приводом, определяется по формуле: Р = Р · FЭФ - РТР - РПР – РС= (Р2 - Р1) · FЭФ - РТР - РПР – РС, где (Р2 - Р2) – разность давлений, действующих по обе стороны днища сильфона; FЭФ – эффективная площадь сильфона; РТР, РПР, РС – силы сопротивления вследствие трения в механизме, действие пружины и упругости самого сильфона. Эффективная площадь сильфонов определяется: 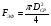 ,где DCP – средний диаметр сильфона, равный 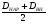 ;(DНАР, DВН – соответственно, наружный и внутренний диаметры сильфона). Поршневые исполнительные механизмы могут использовать большое давление рабочей среды, имеют большие перестановочные усилия на выходном штоке и его большой ход. Поршневые пневматические и гидравлические приводы по количеству силовых органов могут выполнятся одно–, двух– и четырёхпоршневыми; по конструктивной схеме – одностороннего действия (с пружиной) и двухстороннего действия (без пружины); по схеме действия привода – исполнительные поршневые механизмы поступательного действия с односторонним или двухсторонним штоком, исполнительные механизмы, сообщающие приводному органу вращательное движение. Усилие, развиваемое прямоходным приводом, определяется для приводов с двухсторонней подачей давления (рис.35.а): 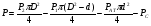 ;для приводов с пружинами (рис.356): 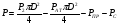 ,где РС – сумма сил сопротивления привода вследствие трения; РПР = с·h – сила, развиваемая пружиной; РАТ – атмосферное давление; Р1,Р2 – избыточные давления по обе стороны поршня; D – диаметр поршня;  Рис.35d – диаметр штока. Скорость движения выходного штока гидравлического исполнительного механизма при полностью открытом проходном сечении золотника постоянна по ходу поршня и может быть определена как 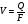 ,где Q – расход среды в цилиндре привода; F – эффективная площадь поршня. Для пневматических поршневых исполнительных механизмов скорости движения выходных штоков могут быть определены после интегрирования следующих дифференциальных уравнений: а) для приводов с двухсторонней подачей давления 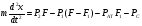 ;б) для приводов с односторонней подачей давления 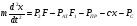 ,где m – масса деталей, участвующих в движении вместе с поршнем, включая 1/3 массы пружины; x – путь поршня; F -площадь поршня; F1 - площадь сечения штока; РАТ - атмосферное давление; Р1, Р2 - разность давлений, действующих на поршень; РС - сумма сил сопротивления движению привода; с - жёсткость пружины; РПР - сила предварительного натяжения пружины (до начала движения поршня).  Рис.36По конструкции и принципу действия плунжерные исполнительные механизмы похожи на поршневые исполнительные механизмы. Но в отличие от поршневых, в которых рабочее давление действует только на торцевую поверхность поршня, в плунжерных – давление среды действует как на торцевую, так и на боковую поверхности плунжера. Так же, как и поршневые механизмы, плунжерные ИМ бывают как одностороннего действия (рис.36.а), так и двухстороннего (рис.36.б). Первые осуществляют поступательное движение приводного органа, вторые – поступательное и вращательное. Тяговое усилие и крутящий момент плунжерных исполнительных механизмов определяют следующим образом: – для плунжерных исполнительных механизмов одностороннего действия 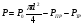 ;– для плунжерных исполнительных механизмов двухстороннего действия 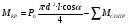 ,где 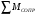 – суммарный момент сопротивления при перемещении плунжера;Р0 – рабочее давление в цилиндре; РПР– усилие сжатия пружины; РТР – усилие трения; l – длина поворотного рычага исполнительного механизма; – угол повороти рычага; d – диаметр плунжера. Исполнительные механизмы с вращающейся лопастью осуществляют вращательное движение приводного органа без дополнительных преобразующих устройств, а также имеют постоянство крутящих моментов по ходу механизма.  Рис.37В этом виде привода (рис.37) неподвижным элементом является цилиндрический корпус, подвижным – лопасть, которая при работе вращается на оси, расположенной в центре корпуса. Для определения величины крутящего момента на валу приведём некоторые предварительные расчёты. Определим суммарное усилие на лопасть: P = (P1 – P2)·F, где Р1, Р2 – давление жидкости (воздуха) по обе стороны лопасти; F - рабочая поверхность лопасти. 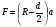 ,где R – радиус лопасти; d – диаметр вала лопасти; а – ширина лопасти. Окончательно для определения силы получим: 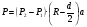 .Если допустить, что сила Р приложена на расстоянии 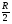 от центра вращения лопасти, то крутящий момент, развиваемый двигателем исполнительного механизма, определится как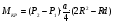 .6. Сравнительная оценка различных исполнительных механизмов В связи с многообразием типов и конструктивных схем исполнительных механизмов возникает сложный вопрос о правильном выборе механизма для того или иного частного случая его применения. На этот вопрос трудно дать однозначный и правильный ответ без чёткого представления о том, по каким путям и по каким достоверным критериям должно осуществляться сопоставление различных исполнительных механизмов. Оценка возможности использования данного исполнительного механизма может быть осуществлена по следующим показателям:
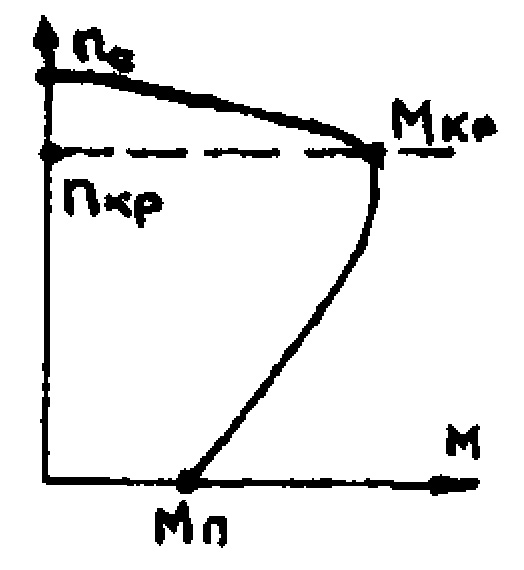
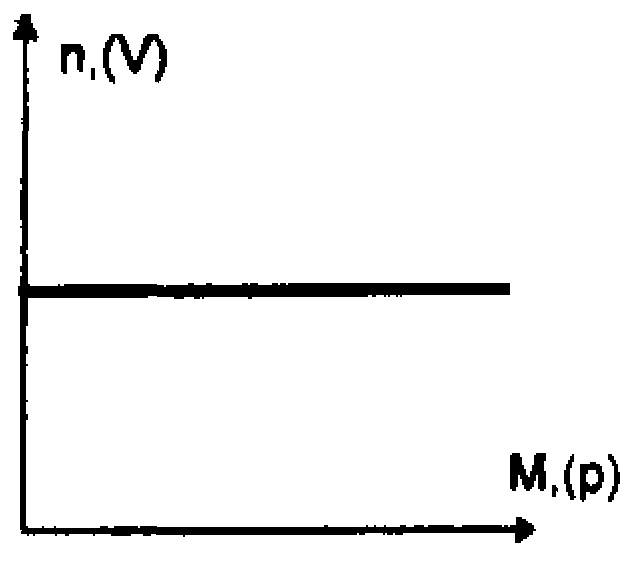
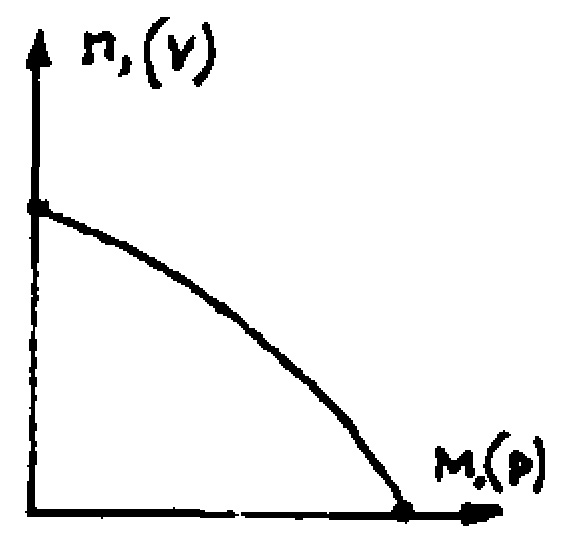
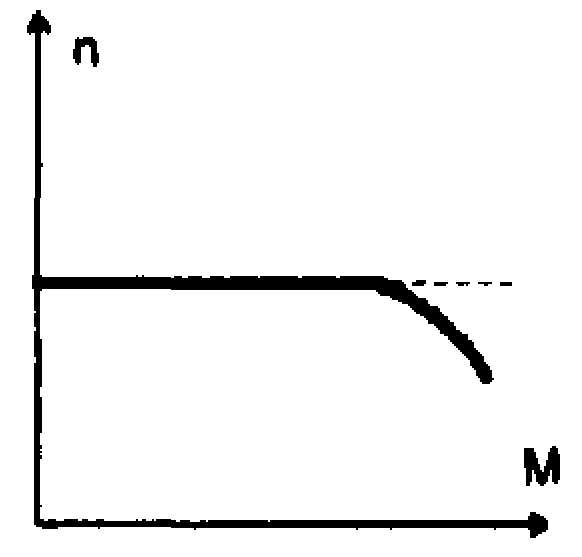
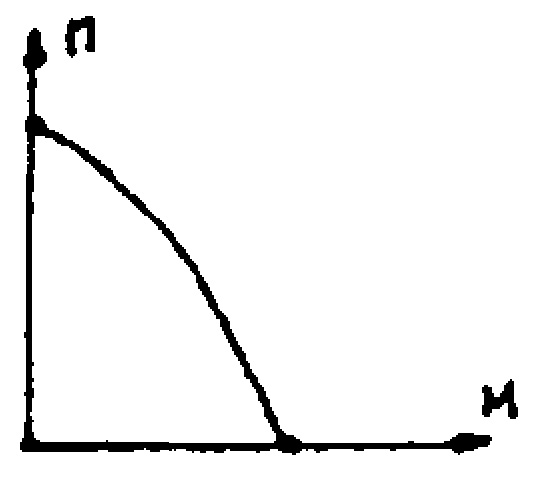
В таблице 6.1 приводятся механические, или внешние характеристики n=f(M) и V=(P) различных типов исполнительных механизмов (где n – число оборотов в минуту; М – крутящий момент; Р – тяговое усилие; V – скорость перемещения), Из этой таблицы следует: 1. Все исполнительные механизмы, имеющие данные характеристики устойчивы в работе. Соблюдается условие 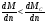 , которое определяет устойчивость системы.2. Приводы на основе электрических асинхронных двигателей, а также все типы гидравлических, использующих в качестве рабочей среды масло, имеют жесткую внешнюю характеристику, т.е. обеспечивают оптимальное постоянство числа оборотов при переменной нагрузке. Пневматические же приводы имеют мягкую характеристику, т.е. обороты выходного вала привода при изменении сил сопротивления резко меняются. 3. Гидравлические и пневматические исполнительные механизмы допускают широкие диапазоны нагрузок по своим характеристикам. Диапазон работы электропривода с асинхронными двигателями весьма мал (ограничивается отрезком nС-nкр). 4. Все виды исполнительных механизмов обладают достаточной величиной пусковых моментов и могут надёжно работать при перегрузках. Таблица 6.1.
Ко второй группе критериев сравнения относят технико-экономические показатели исполнительных механизмов. Большинство из них следует выражать в относительных единицах по отношению к развиваемой мощности:
Следует учитывать, что технико-экономические показатели ИМ любого принципа действия значительно улучшаются при увеличении крутящего момента, развиваемого его выходным валом, или тяговое усилие штока. Поэтому сравнение различных типов ИМ по технико-экономическим показателям нужно вести при одних и тех же величинах крутящих моментов и тяговых усилий. Основные технико-экономические показатели для пневматических и гидравлических ИМ не являются постоянными и зависят от используемого рабочего давления жидкости или газа. КПД электрических ИМ находится в пределах =0,50,85 (в зависимости от типа редуктора), КПД гидравлических ИМ находится в пределах =0,60,9, КПД пневматических ИМ – =0,10,3. Таким образом, с этой точки зрения пневматические исполнительные механизмы являются наименее экономичными. Однако при выборе того или иного исполнительного механизма нельзя ограничиваться рассмотрением только технико-экономических показателей приводов, включающих только двигатель и редуктор, следует рассматривать всю систему в целом, включая насосную установку, компрессор, пусковые устройства и агрегаты, защитные устройства и т.д. Оценив всю систему комплексно, можно сделать правильные выводы о целесообразности применения того или иного типа исполнительного механизма. К третей группе критериев сравнения исполнительных механизмов относятся технико-эксплуатационные качества:
Основные характеристики исполнительных механизмов рассматривались в предыдущих разделах данного методического указания, Сравнивая их, можно сделать вывод, что все они имеют различные технико-эксплуатационные показатели, с точки зрения которых каждый тип исполнительного механизма обладает определёнными достоинствами и недостатками. Выбор исполнительного механизма по этим показателям диктуется конкретными требованиями производственного процесса, определяющего условия длительной эксплуатации данного механизма. 7. ИСПОЛНИТЕЛЬНЫЕ МЕХАНИЗМЫ В АВТОМАТИЗИРОВАННЫХ ПРИВОДАХ ШВЕЙНЫХ МАШИН В настоящее время промышленные швейные машины общего и специального назначения в основном оснащаются автоматизированными приводами, выпускаемыми фирмами "Эфка", "Квик-Ротан", "Мицубиси". Оснащение универсальной швейной машины такими приводами и дополнительными механизмами позволяет автоматизировать ряд технологических переходов в процессе выполнения операций. К ним относятся:
В автоматизированном электроприводе швейных машин с электронным управлением могут использоваться асинхронный трёхфазный электродвигатель с короткозамкнутым ротором, специальный коллекторный электродвигатель постоянного тока или шаговый электродвигатель с ЧПУ. Однако преимущественное применение в неавтоматизированном и автоматизированном приводах швейных машин получили асинхронные трёхфазные электродвигатели с короткозамкнутым ротором. Известно, что при отсутствии нагрузки синхронная частота вращения магнитного поля статора n0 определяется зависимостью n0=60f/P, где f – частота питающего напряжения сети, Р – число пар полюсов. | ||||||||||||||||
