|
|
Мет_ЛР_ТССА_2017_2. Методичні вказівки до лабораторних робіт з дисциплін теорія систем та системний аналіз
Таке впорядкування утворює нестрогий лінійний порядок.
Для відношення нестрогого лінійного порядку доведено існування числової системи із стосунками нерівності і рівності між числами, що описують властивості об'єктів. Будь-які дві числові системи для нестрогого лінійного порядку зв'язано між собою монотонним перетворенням. Отже, ранжируванням за умови наявності еквівалентних об'єктів є вимір також в порядковій шкалі.
У практиці ранжирування об'єктів, між якими допускаються відношення як строгого порядку, так і еквівалентності, числове представлення вибирається таким чином. Найбільш переважному об'єкту привласнюється ранг, рівний одиниці, другому по перевазі – ранг, рівний двом, і так далі Для еквівалентних об'єктів зручно з точки зору технології подальшої обробки експертних оцінок призначати однакові ранги, рівні середньоарифметичному значенню рангів, що привласнюються однаковим об’єктам. Такі ранги називають зв'язаними рангами. Тоді на прикладі, коли для об’єктів 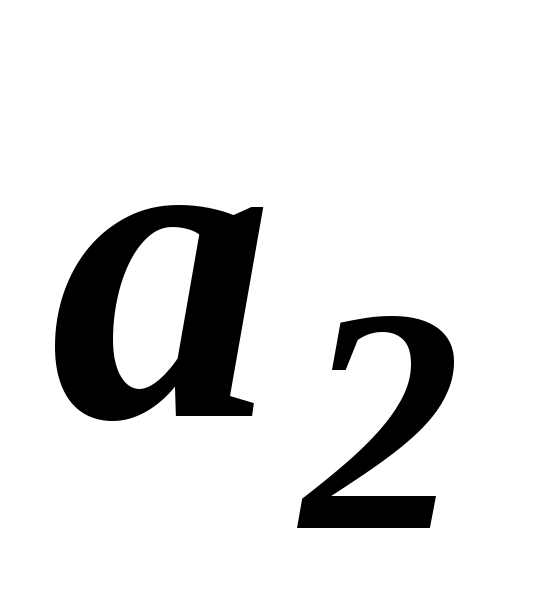 , , 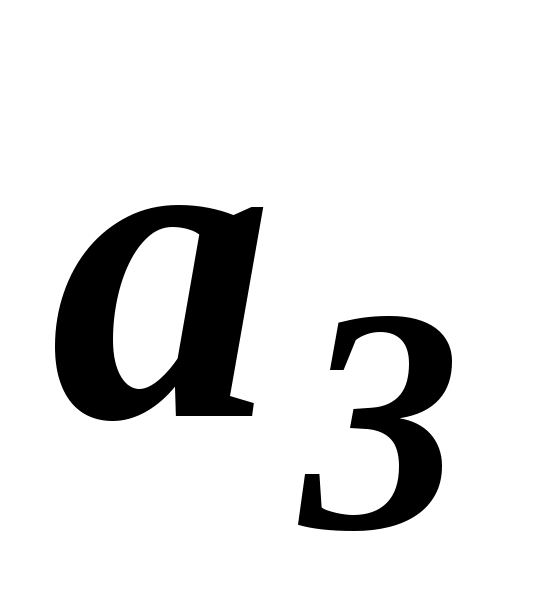 оцінки оцінки 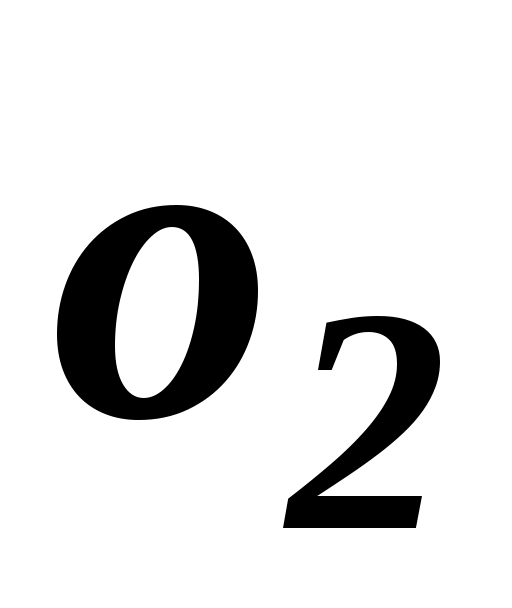 та та 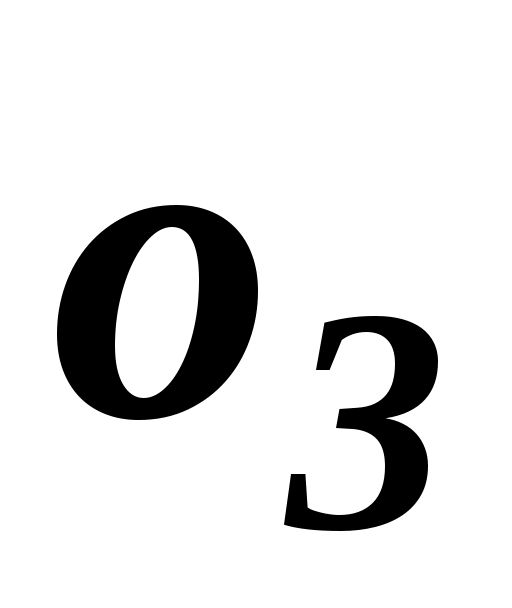 збігаються, для нестрогого лінійного порядку впорядкування, визначаються рівні ранги збігаються, для нестрогого лінійного порядку впорядкування, визначаються рівні ранги 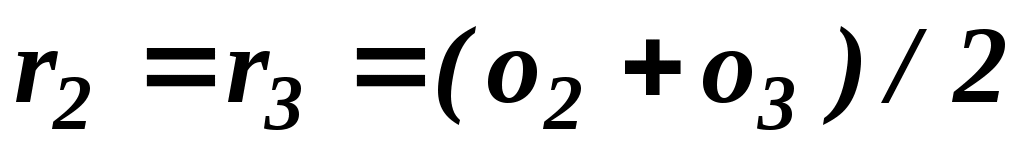 . Зв'язані ранги можуть виявитися дробовими числами. Зручність використання зв'язаних рангів полягає в тому, що сума рангів . Зв'язані ранги можуть виявитися дробовими числами. Зручність використання зв'язаних рангів полягає в тому, що сума рангів  об'єктів дорівнює сумі натуральних чисел від одиниці до об'єктів дорівнює сумі натуральних чисел від одиниці до  . При цьому будь-які комбінації зв'язаних рангів не змінюють цю суму. Дана обставина істотно спрощує обробку результатів ранжирування при груповій експертній оцінці. . При цьому будь-які комбінації зв'язаних рангів не змінюють цю суму. Дана обставина істотно спрощує обробку результатів ранжирування при груповій експертній оцінці.
При груповому ранжируванні кожен 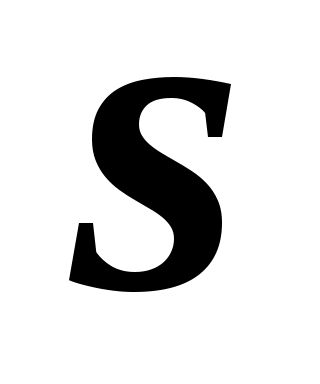 -й експерт привласнює кожному -й експерт привласнює кожному 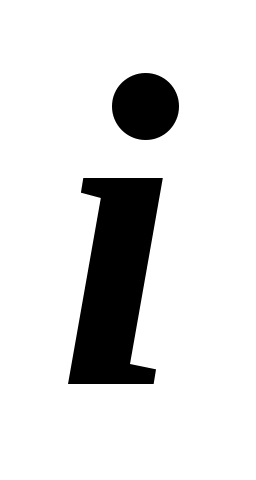 -у об'єкту ранг -у об'єкту ранг 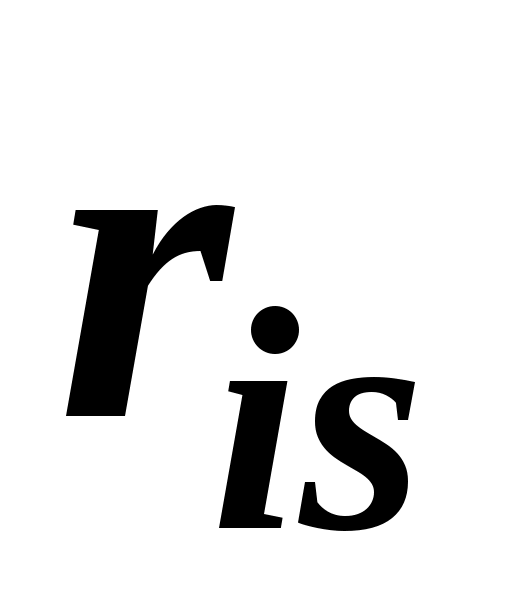 . В результаті проведення експертизи виходить матриця рангів . В результаті проведення експертизи виходить матриця рангів  розмірності розмірності  , де , де 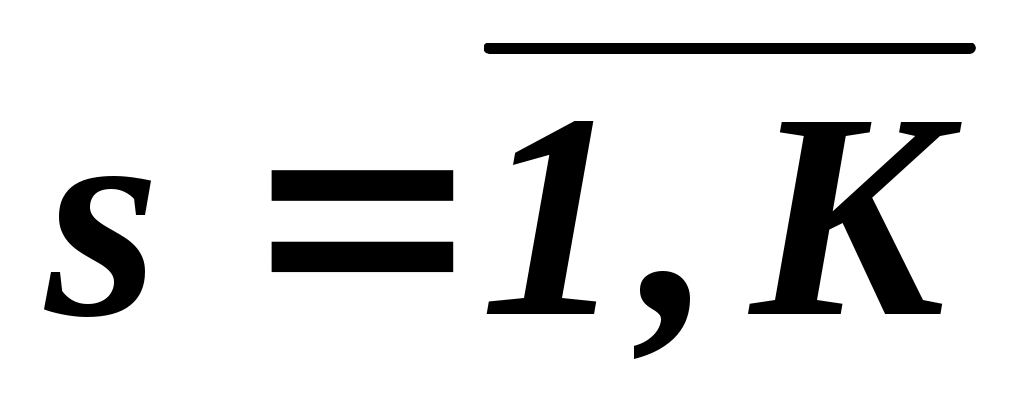 – число експертів; – число експертів; 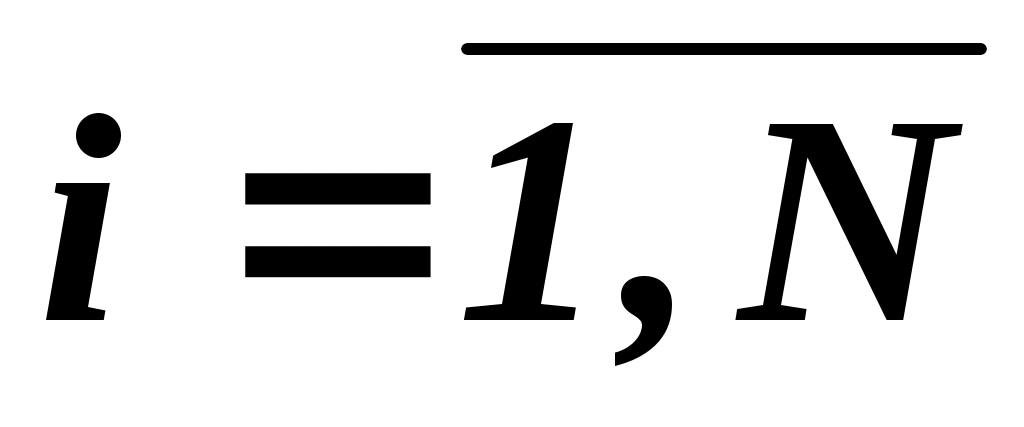 – число об'єктів. Результати групового експертного ранжирування представляються у вигляді таблиці. 2.3. – число об'єктів. Результати групового експертного ранжирування представляються у вигляді таблиці. 2.3.
Таблиця 2.3 – Результати групового ранжирування
Далі здійснюється процедура ранжирування складних систем. На основі групового експертного ранжирування (табл. 2.2) можна визначити результуючий порядок переваги думки цілої групи даних експертів. Для цього необхідно визначити сумарні ранги кожної системи
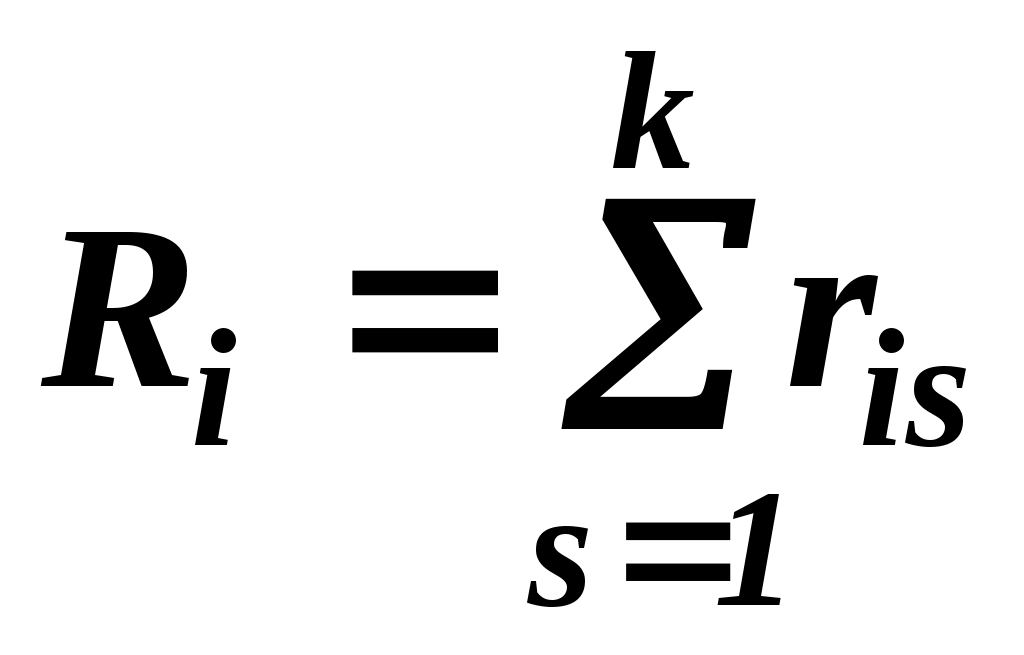 ; ;
|
(2.4)
|
Найбільш важливій системі приписується ранг « », найменш важливій системі – ранг « », найменш важливій системі – ранг « » і так далі. » і так далі.
Для наочності уявлення про міру узгодженості точок зору двох будь-яких експертів 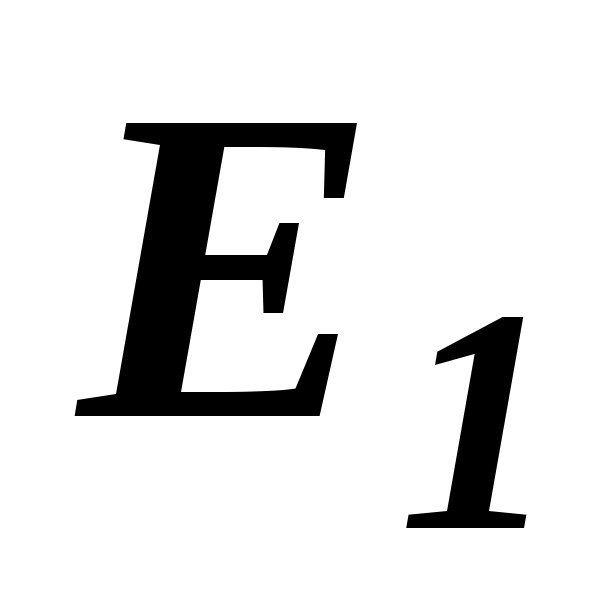 і і 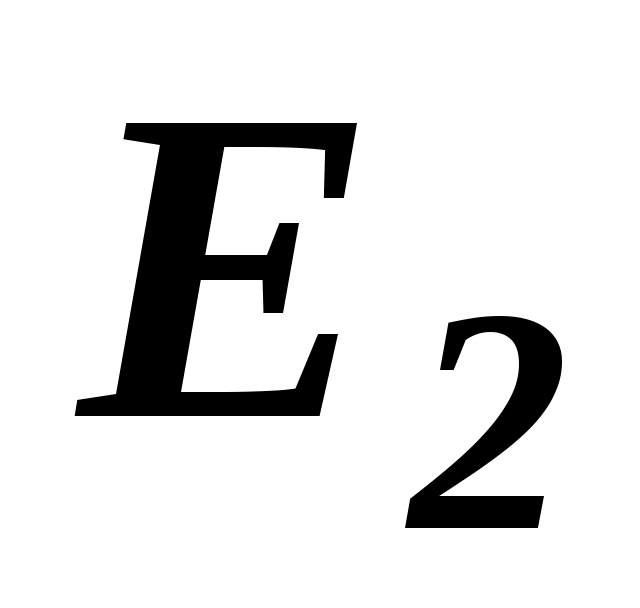 служить коефіцієнт Спірмена служить коефіцієнт Спірмена 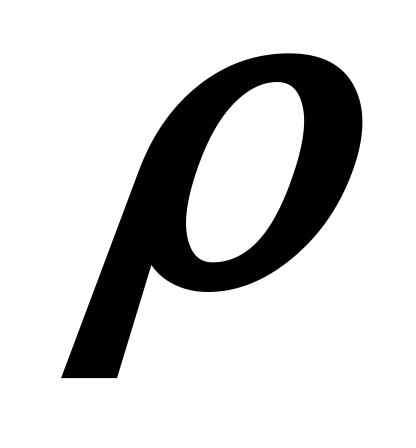 (коефіцієнт парної рангової кореляції). Наприклад, можна використовувати коефіцієнт Спірмена у вигляді (коефіцієнт парної рангової кореляції). Наприклад, можна використовувати коефіцієнт Спірмена у вигляді
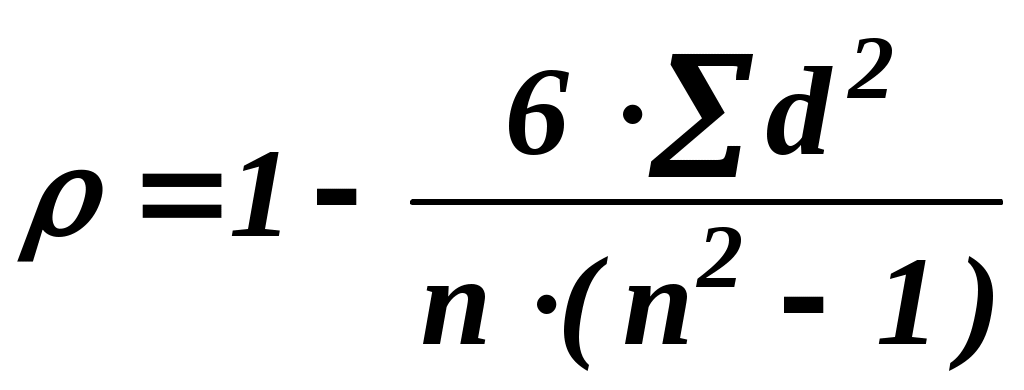 ; ;
|
(2.3)
|
де  ‑ кількість об’єктів, що оцінюються, а ‑ кількість об’єктів, що оцінюються, а 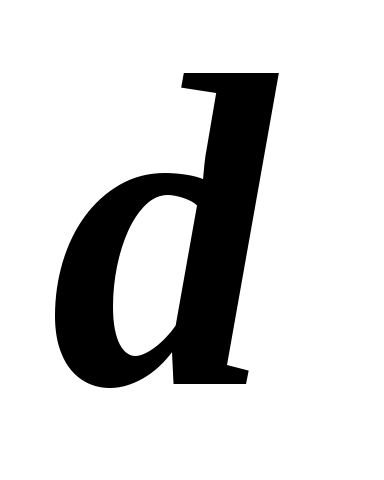 ‑ різниця рангів. ‑ різниця рангів.
Коефіцієнт Спірмена приймає значення 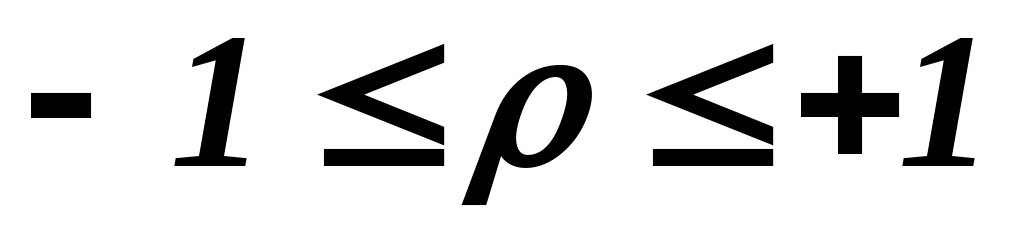 . Значення . Значення 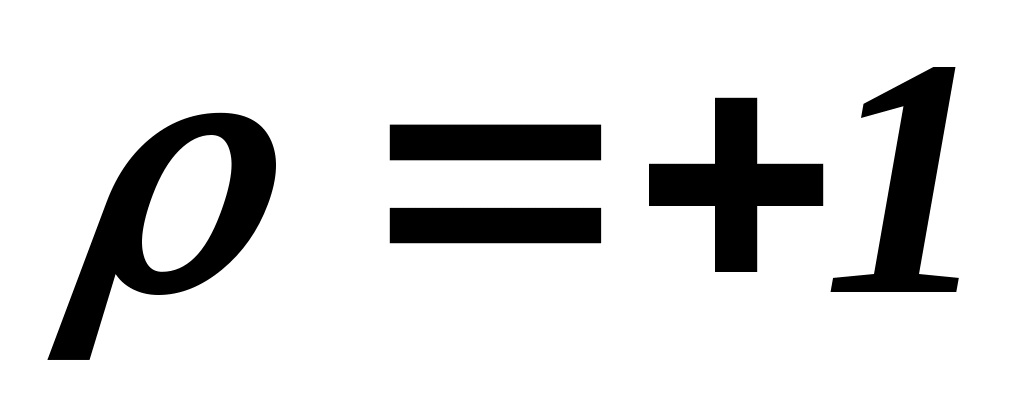 відповідає повному збігу оцінок в рангах двох експертів (повна узгодженість думок двох експертів), а значення відповідає повному збігу оцінок в рангах двох експертів (повна узгодженість думок двох експертів), а значення 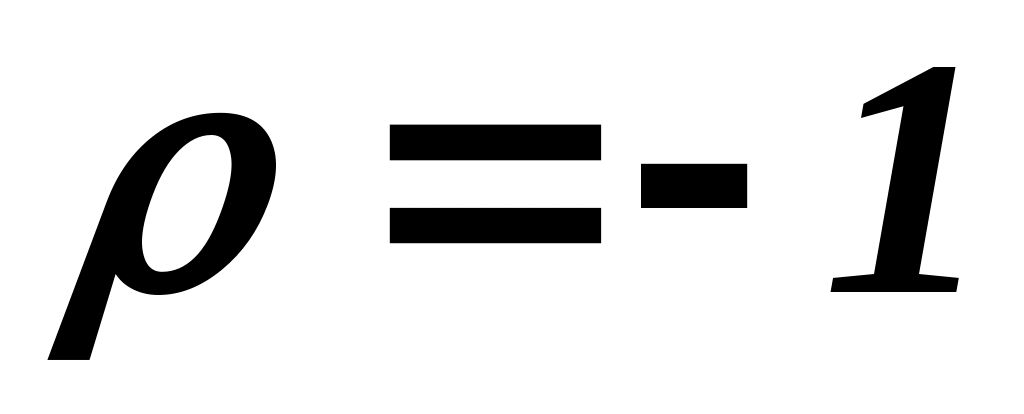 – двом взаємно протилежним ранжируванням важливості властивостей (думка одного експерта протилежна до думки іншого). – двом взаємно протилежним ранжируванням важливості властивостей (думка одного експерта протилежна до думки іншого).
1.4.2.1 Порядок виконання завдання 2
Для виконання індивідуального завдання значення показників оцінок експертів 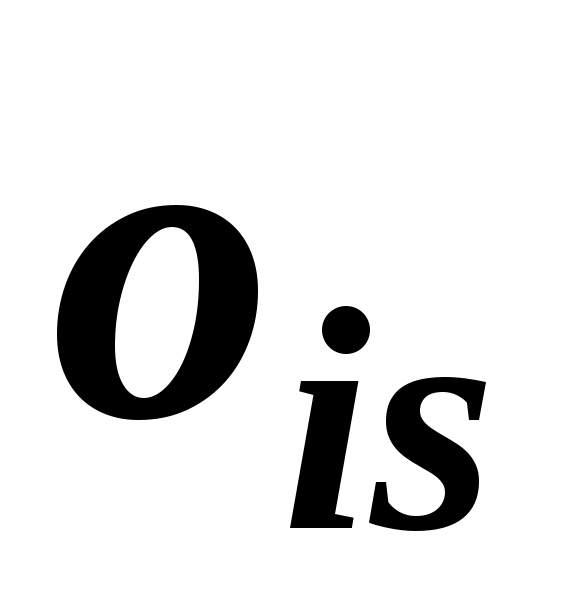 необхідно отримати за допомогою генератора псевдовипадкових чисел, рівномірно розподілених в інтервалі необхідно отримати за допомогою генератора псевдовипадкових чисел, рівномірно розподілених в інтервалі 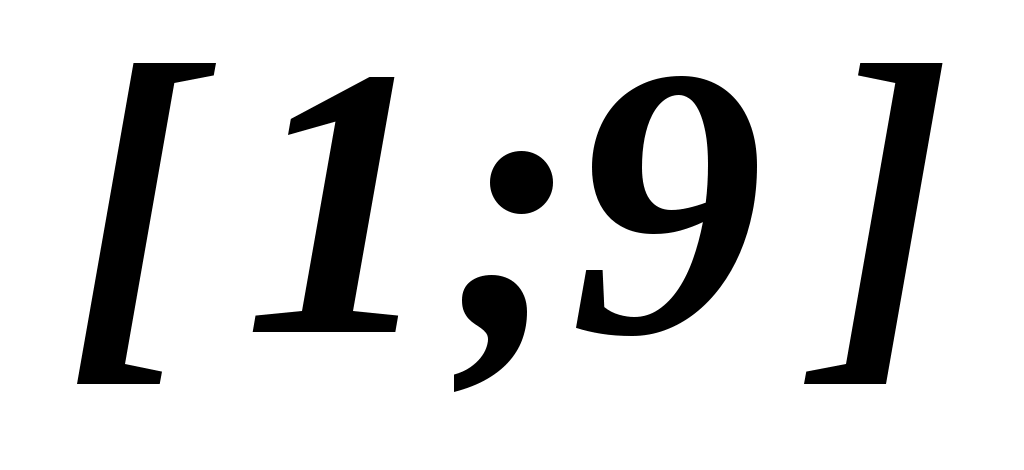 . Данні моделювання представляються у вигляді табл. 2.4. . Данні моделювання представляються у вигляді табл. 2.4.
Таблиця 2.4 – Оцінки експертів
Метод парного порівняння є процедурою встановлення переваги об'єктів при порівнянні всіх можливих пар. При порівнянні пари об'єктів можливо або відношення строгого порядку, або відношення еквівалентності.
В результаті порівняння пари об'єктів  , ,  експерт упорядковує їх, висловлюючи або експерт упорядковує їх, висловлюючи або 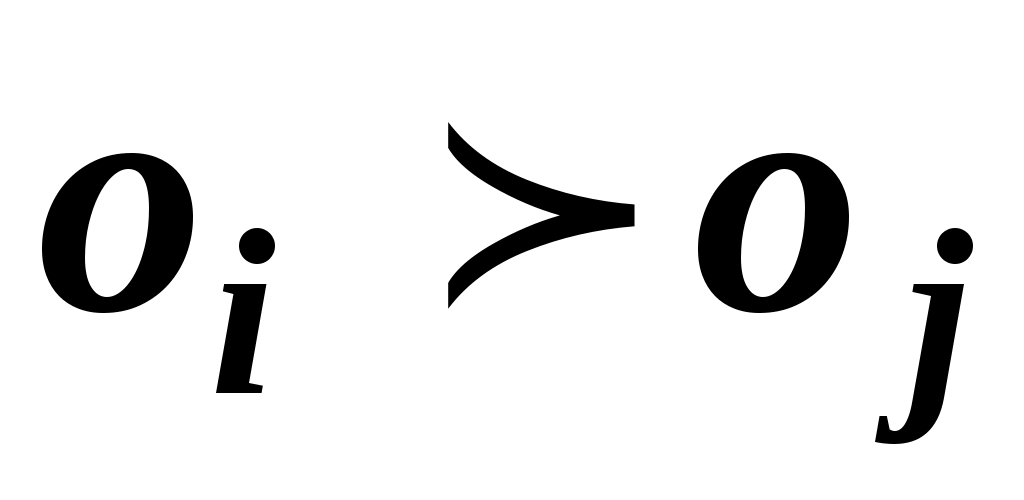 , або , або  , або , або 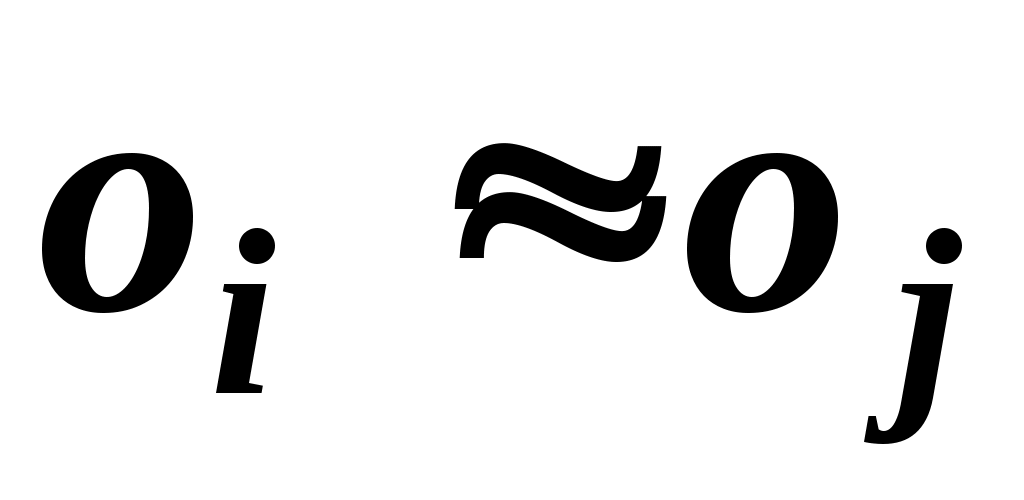 . Вибір числової представлення . Вибір числової представлення 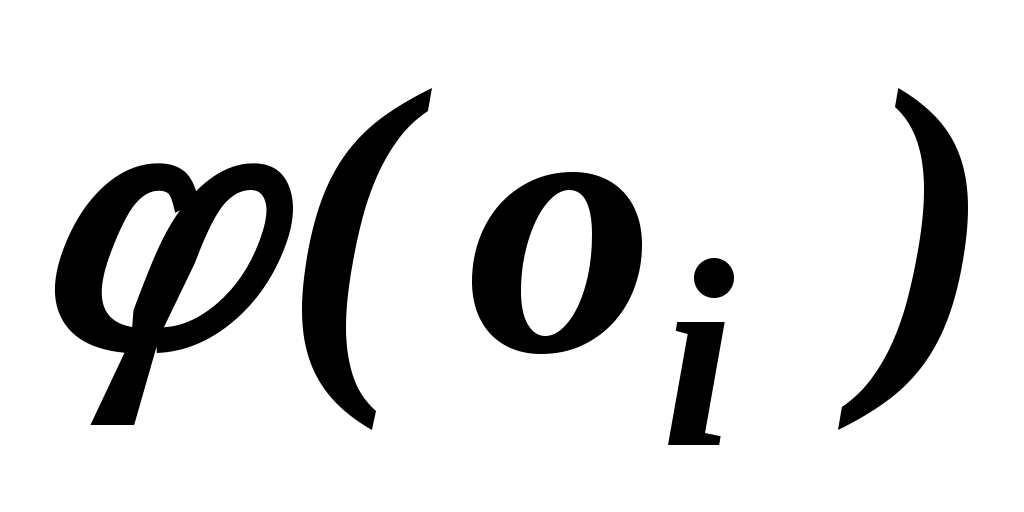 можна виробити так: якщо можна виробити так: якщо 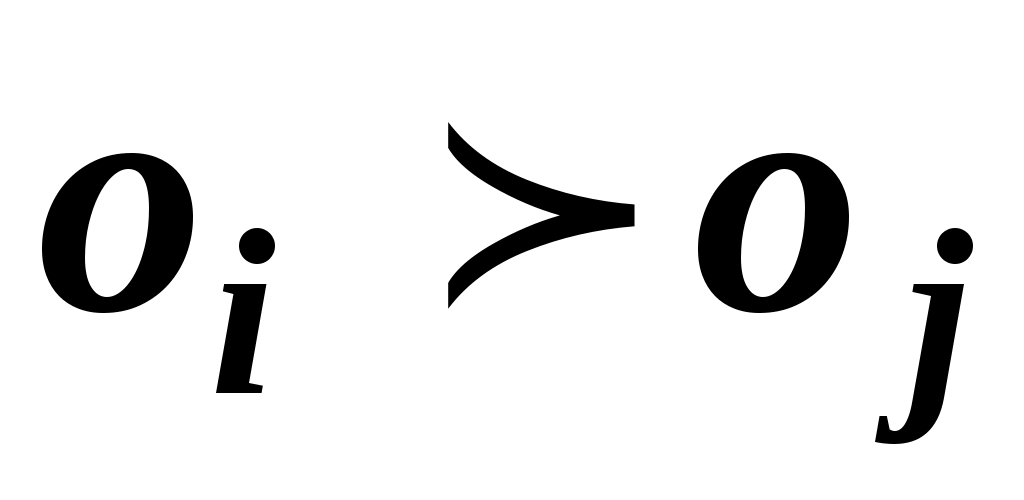 , то , то 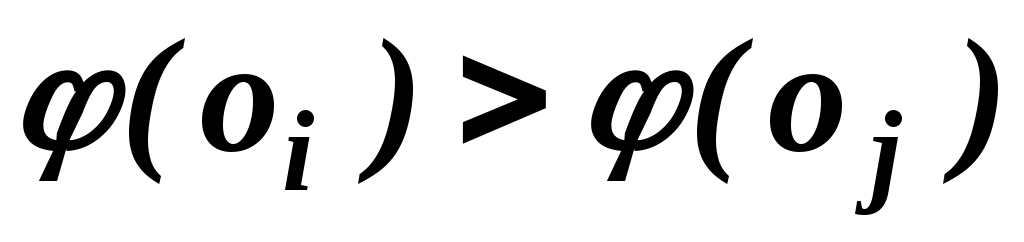 ; якщо перевага в парі зворотна, то знак нерівності замінюється на зворотний, тобто ; якщо перевага в парі зворотна, то знак нерівності замінюється на зворотний, тобто 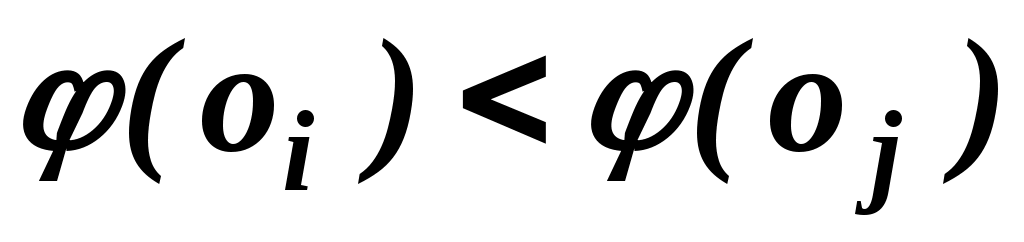 . Якщо об'єкти еквівалентні, то можна вважати, що . Якщо об'єкти еквівалентні, то можна вважати, що 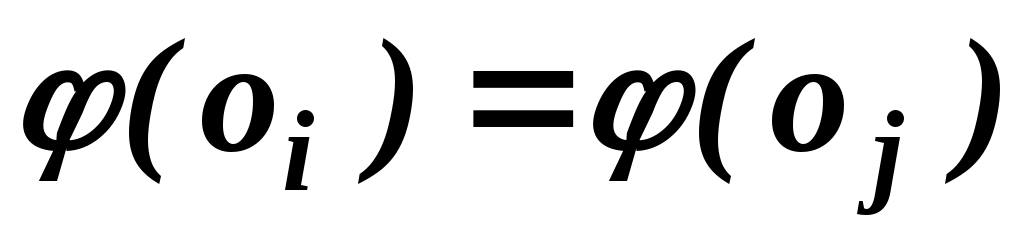 . .
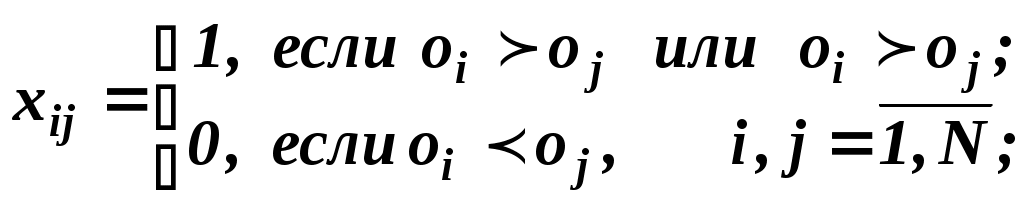 . .
|
(2.4)
|
На практиці може застосовуватися не лише формула (2.4), але і враховуватися міра переваги 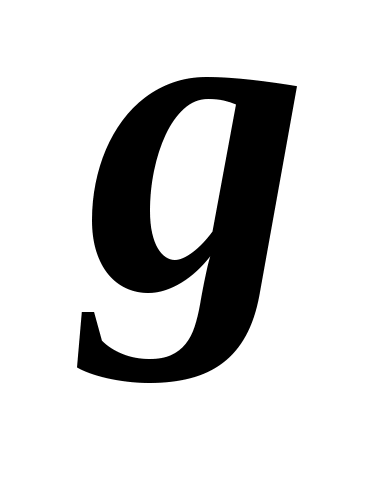 одного і того ж одного і того ж 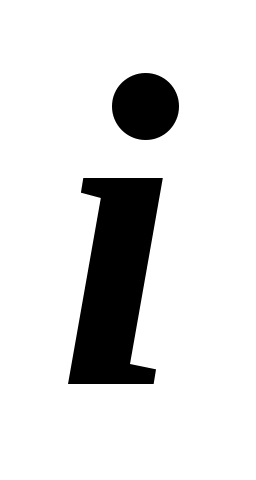 -го об'єкту, який оцінюється -го об'єкту, який оцінюється 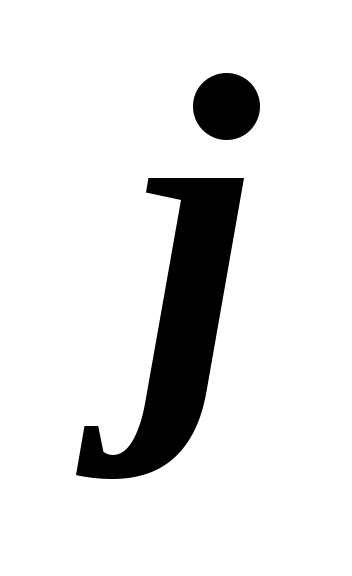 -м ( -м (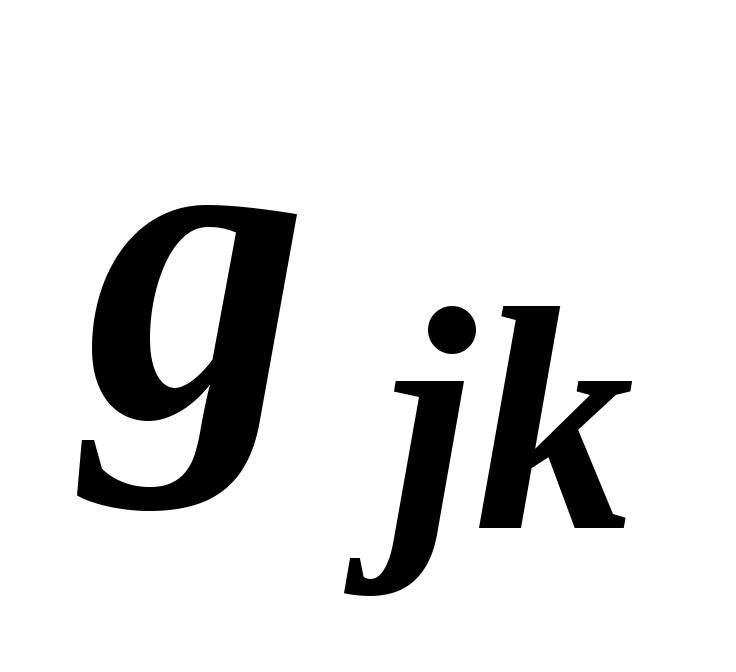 ) і ) і 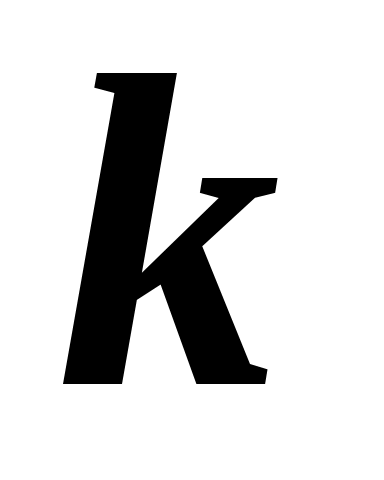 -м експертами ( -м експертами ( ). ).
Розглянемо приклад визначення міри переваги 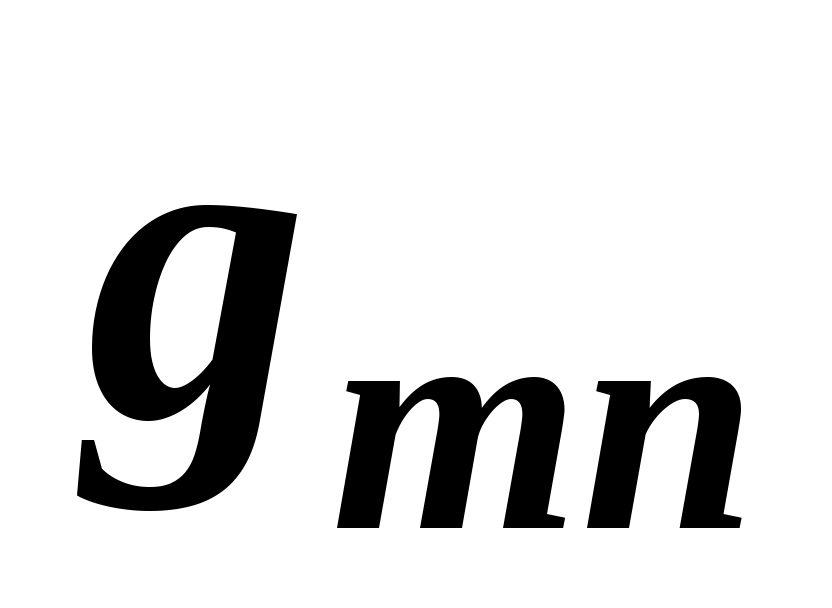 об’єкту об’єкту 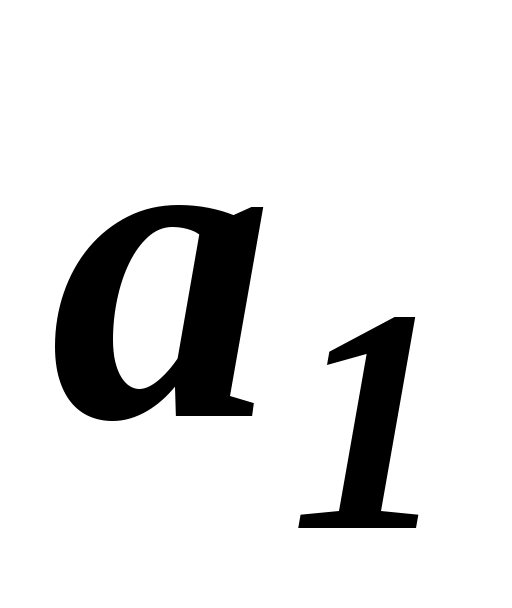 , що виражається , що виражається  експертами за шкалою Сааті значеннями від « експертами за шкалою Сааті значеннями від « » до « » до « ». Якщо індекс першого експерта ». Якщо індекс першого експерта  , а другого , а другого 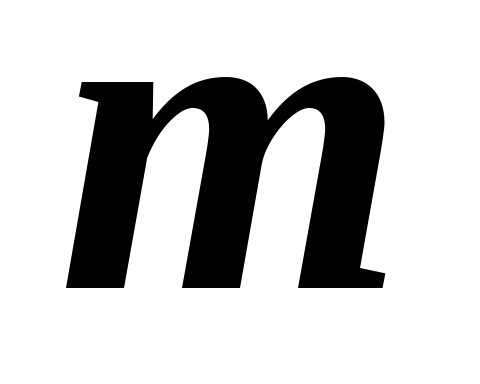 , то міра переваги дорівнює , то міра переваги дорівнює
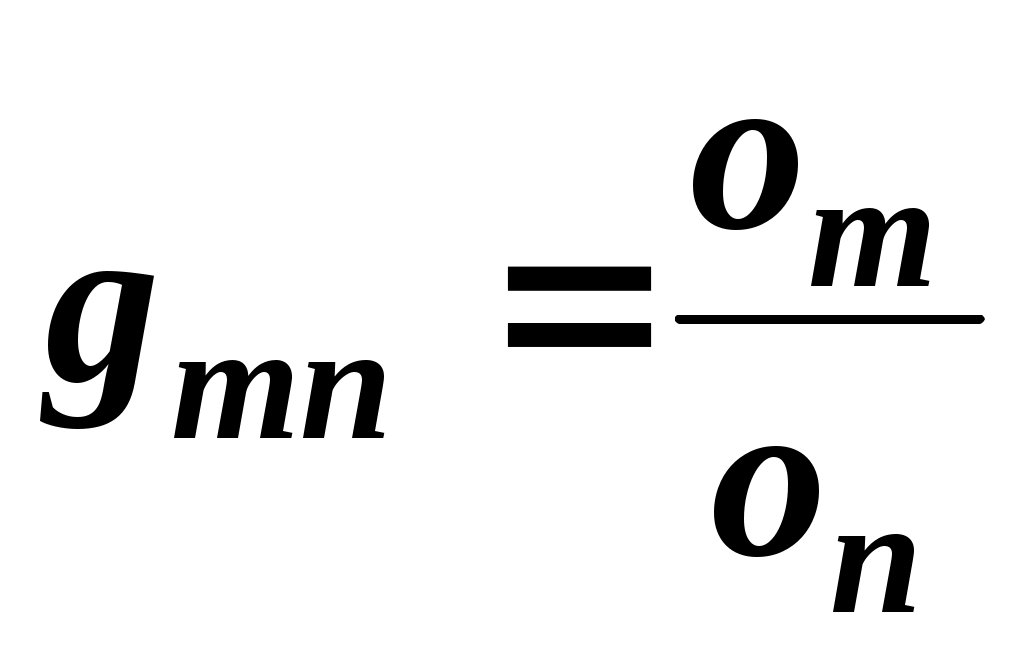 , ,
|
(2.5)
|
де 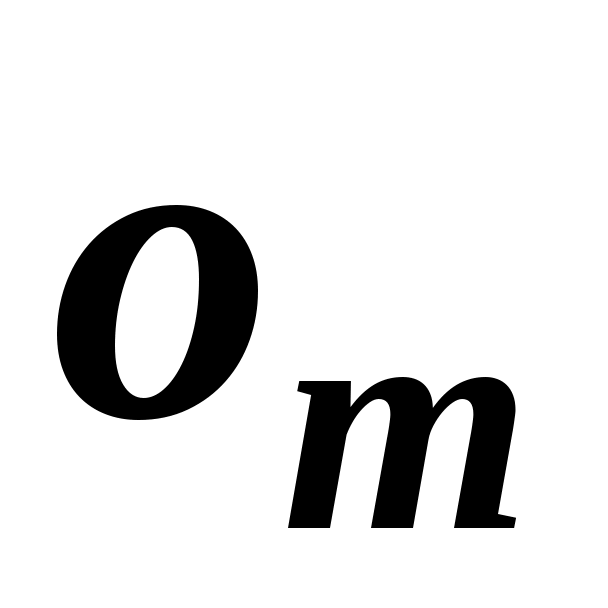 та та 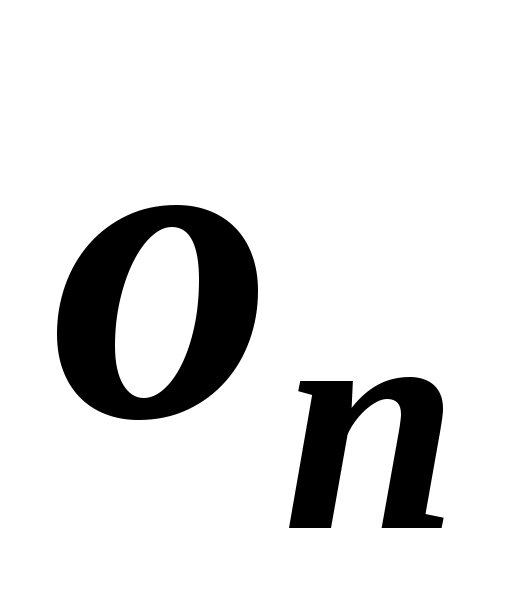 відповідні оцінки одного і того ж об’єкту експертами з номерами відповідні оцінки одного і того ж об’єкту експертами з номерами 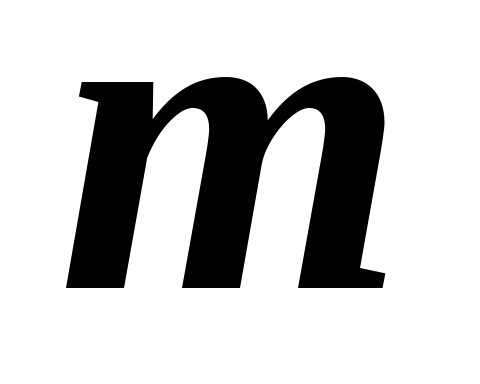 та та  . .
У разі, коли 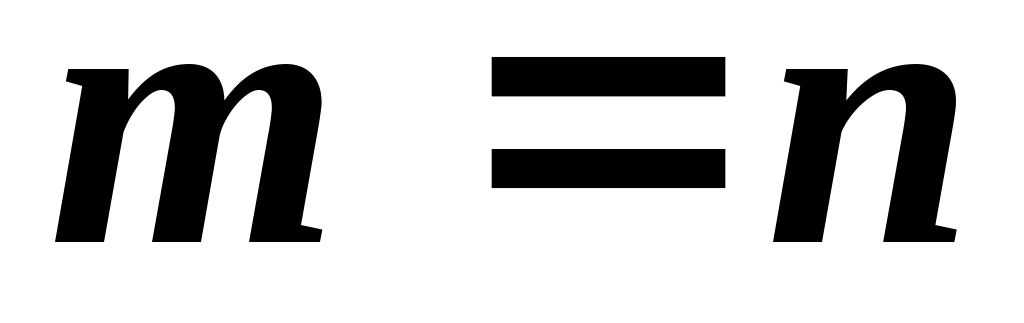 , міра переваги дорівнює « , міра переваги дорівнює « ». Тобто значення елементів головної діагоналі матриці парних порівнянь ». Тобто значення елементів головної діагоналі матриці парних порівнянь 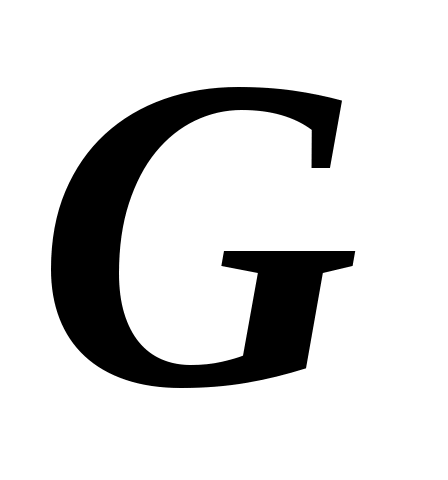 завжди дорівнюють одиниці. Таким чином, матриця оцінки точок зору завжди дорівнюють одиниці. Таким чином, матриця оцінки точок зору 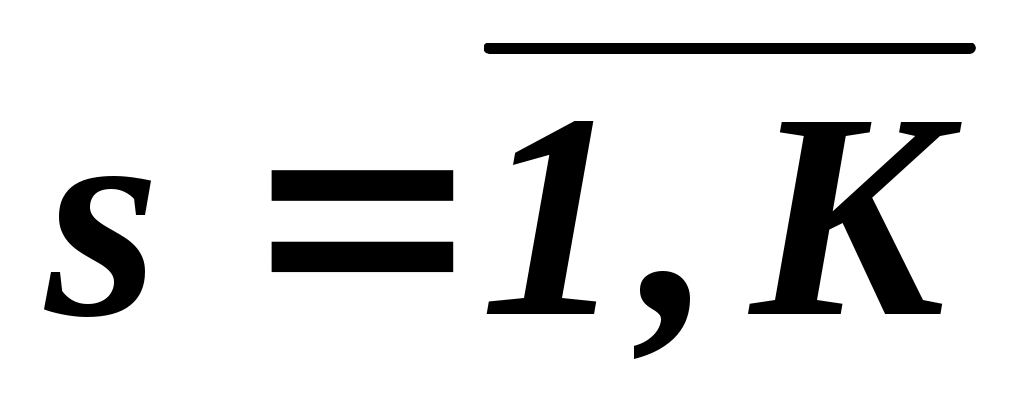 експертів набуває вигляду, який може бути представленим у виді табл. 2.2. експертів набуває вигляду, який може бути представленим у виді табл. 2.2.
Після того, як матриця (табл..2.5) сформована проводиться оцінка узгодженості думок експертів. Для визначення міри узгодженості складеної експертом матриці використовується вивід про те, що якщо матриця погоджена, то найбільше її власне значення 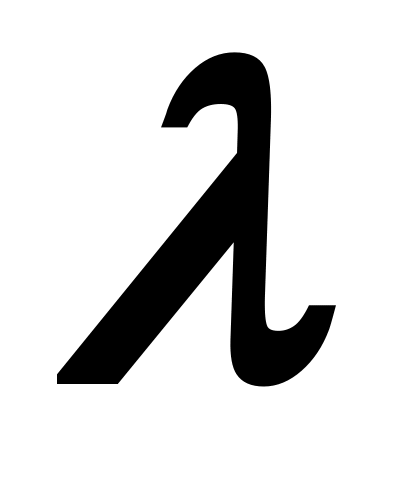 дорівнює порядку матриці дорівнює порядку матриці  , а останні значення , а останні значення 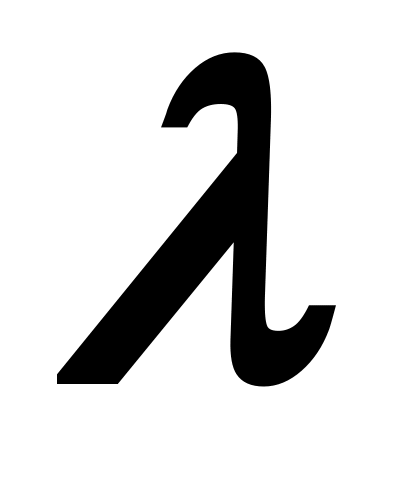 дорівнюють нулю. Як оцінка неузгодженості вихідних суб'єктивних оцінок використовуємо значення відношення узгодженості ( дорівнюють нулю. Як оцінка неузгодженості вихідних суб'єктивних оцінок використовуємо значення відношення узгодженості (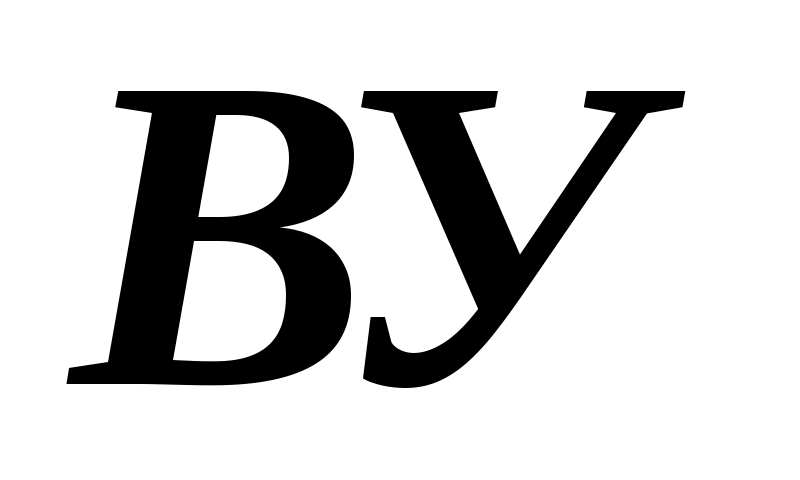 ). Якщо ). Якщо 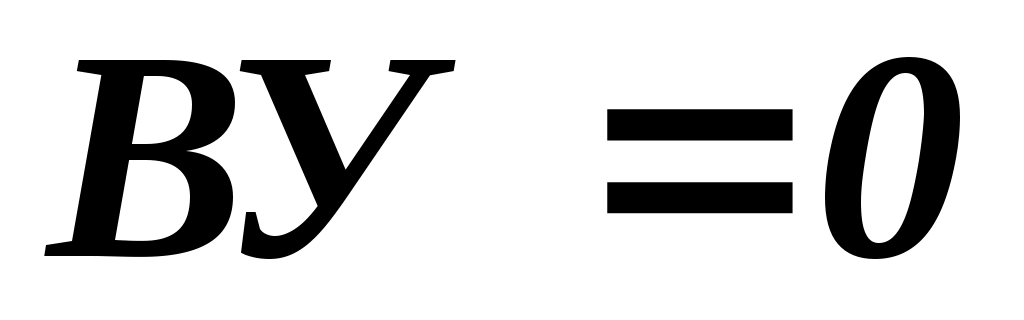 , то всі оцінки погоджені, якщо , то всі оцінки погоджені, якщо 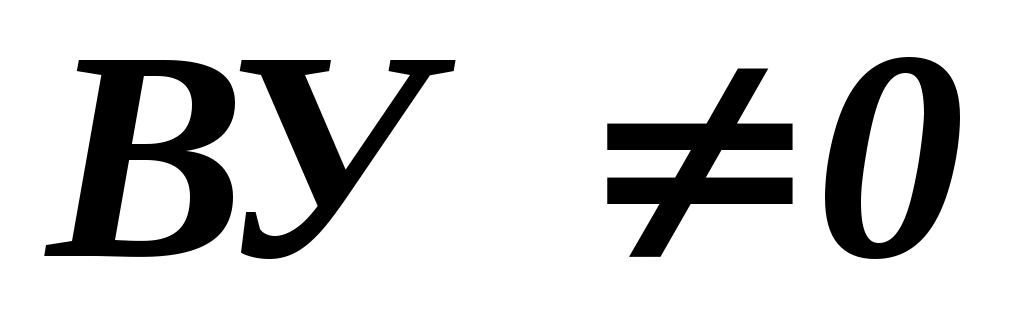 , то не погоджені. Чим більше значення , то не погоджені. Чим більше значення 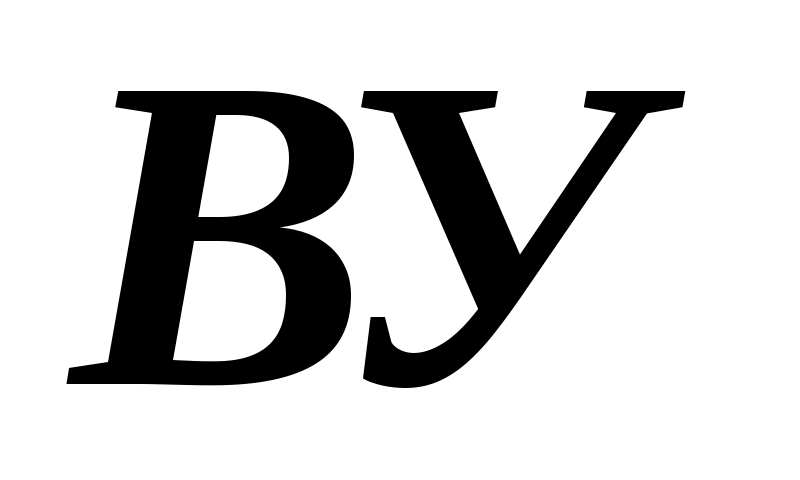 , тим менш погоджені експертні оцінки. Величина , тим менш погоджені експертні оцінки. Величина 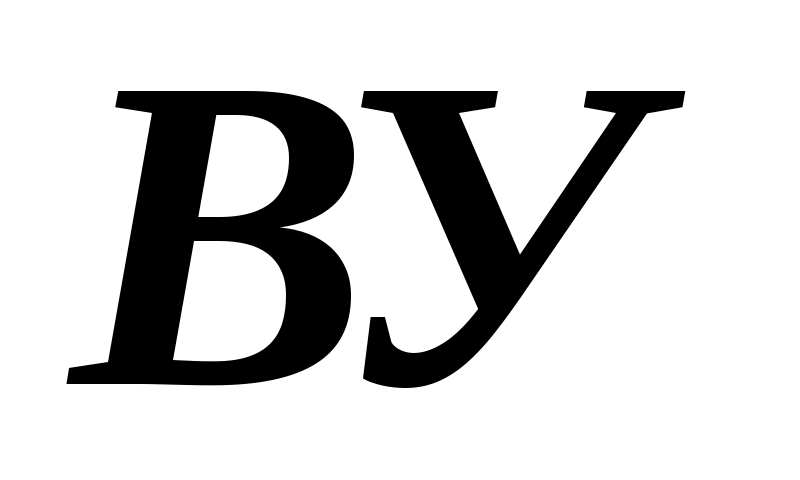 має бути не більше має бути не більше  , щоб бути прийнятною. Якщо виявиться що , щоб бути прийнятною. Якщо виявиться що 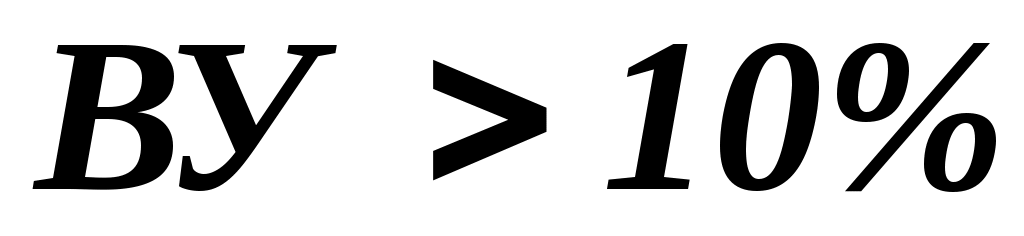 , тоді експертові пропонується переглянути свої оцінки. , тоді експертові пропонується переглянути свої оцінки.
Таблиця 2.5 – Матриця оцінки точок зору експертів
На практиці як міру узгодження розглядають нормоване відхилення 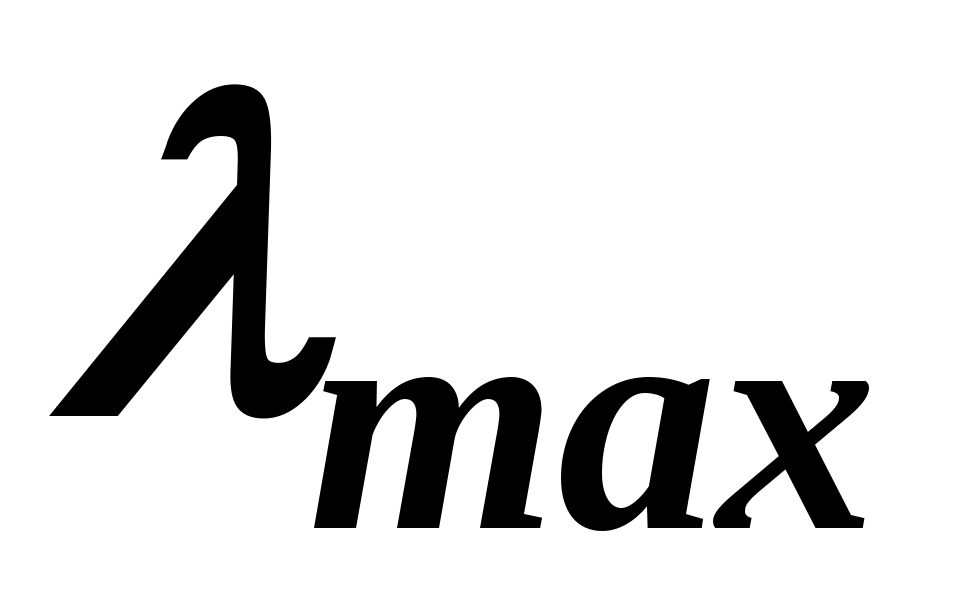 від від  , яке називається індексом узгодженості ( , яке називається індексом узгодженості (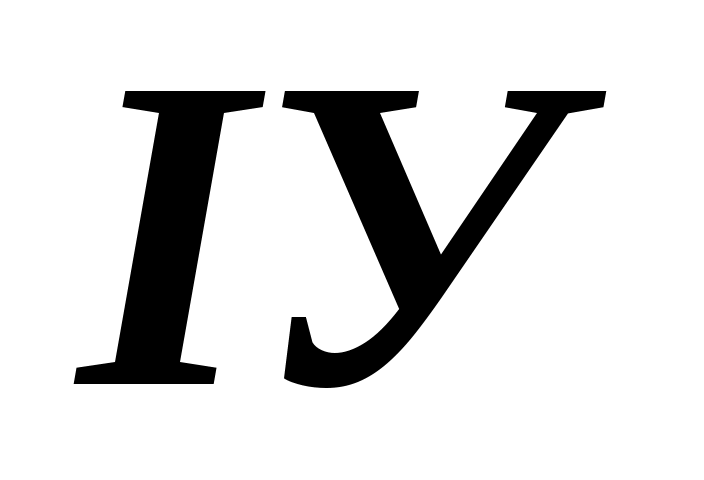 ): ):
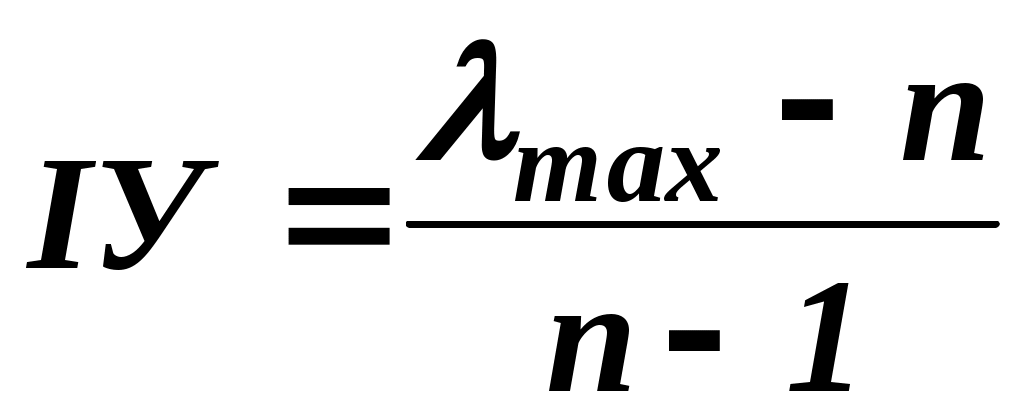 . .
|
(2.6)
| |
|
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb.
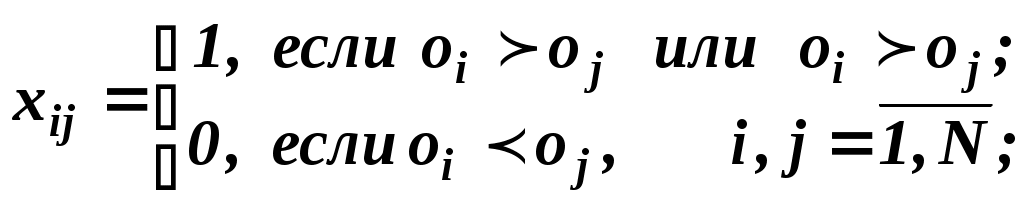 .
.