Методика изучения величин. Методика изучения величин

• Название: Методика изучения величин
• Дата: 28.09.2022
• Размер: 185.5 Kb.
• Имя файла: Методика изучения величин.doc
• Тип: Документы; #703370

МЕТОДИКА ИЗУЧЕНИЯ ВЕЛИЧИН

В начальных классах рассматриваются величины: длина, площадь, масса, емкость, время и др. Учащиеся должны полу­чить конкретные представления об этих величинах, ознакомить­ся с единицами их измерения, овладеть умениями измерять ве­личины, научиться выражать результаты измерения в различ­ных единицах, выполнять арифметические действия над вели­чинами.

Изучение величин имеет большое значение, так как поня­тие величины является важнейшим понятием математики. Каж­дая изучаемая величина — это некоторое обобщенное свойство реальных объектов окружающего мира. Упражнения в измере­ниях развивают пространственные представления, вооружают учащихся важными практическими навыками, которые широко применяются в жизни. Следовательно, изучение величин — это одно из средств связи обучения с жизнью.

Величины рассматриваются с I по IV класс в тесной связи с изучением натуральных чисел и дробей: обучение измерению связывается с обучением счету; новые единицы измерения вво­дятся вслед за введением соответствующих счетных единиц; арифметические действия выполняются над натуральными чис­лами и над величинами. Измерительные и графические работы как наглядное средство используются при решении задач. Та­ким образом, изучение величин способствует усвоению многих вопросов курса математики.
Длина отрезка

Первые представления о длине как свойстве предметов у детей возникают задолго до школы. К началу обучения в шко­ле дети выделяют, как правило, без ошибок линейную протя­женность (длину, ширину, высоту предметов, расстояние между ними). Они правильно устанавливают отношения: длиннее — короче, шире — уже, дальше — ближе и т.п., если различия в этом плане ярко выражены, а по другим свойствам предметы сходны (например, имеют одинаковую форму, изготовлены из одного материала и т.п.).

С первых дней обучения в школе ставится задача уточнять пространственные представления детей. Этому помогают упраж­нения на сравнение предметов по протяженности, например: «Какая книга тоньше (книги прикладываются друг к другу)? Кто ниже: Саша или Оля (дети становятся рядом)? Что глуб­же: ручей или река (по представлению)?» В процессе этих уп­ражнений отрабатывается умение сравнивать предметы по дли­не, а также обобщается свойство, по которому происходит срав­нение— линейная протяженность, длина.

Важным шагом в формировании данного понятия является знакомство с прямой линией и отрезком как «носителем» ли­нейной протяженности, лишенным по существу других свойств. Сравнивая отрезки на глаз, дети получают представление об одинаковых и неодинаковых по длине отрезках.

На следующем этапе происходит знакомство с первой едини­цей измерения отрезков. Из множества отрезков выделяется отрезок, который принимают за единицу. Дети узнают его название и приступают к измерению с помощью этой единицы. Имеются различные точки зрения по вопросу о том, какую еди­ницу измерения вводить первой. В жизненной практике дети наблюдают чаще всего измерение с помощью метра. Метр — ос­новная единица длины. Метр существует в виде отдельного эта­лона (мерки). С помощью его учителю легко показать процесс измерения (как откладывается мерка на отрезке, как происхо­дит подсчет единиц измерения). Поэтому некоторые методисты рекомендуют первой единицей измерения вводить метр. Однако при рассмотрении метра трудно провести достаточное количе­ство упражнений в измерении отрезков так, чтобы работал каж­дый ученик, что совершенно необходимо для понимания самого процесса измерения. Другие методисты предлагают первой еди­ницей измерения ввести сантиметр (так дано и в программе), что позволит каждому ученику выполнить, сидя за партой, большое количество работ по измерению. Это не исключает воз­можности на подготовительном этапе, опираясь на жизненные наблюдения детей, вспомнить, как и чем измеряют тесьму, тка­ни, ленту и т.п., отмерить для примера 2–3 м шпагата или из­мерить длину доски. Не устанавливая соотношений между мет­ром и сантиметром, можно ввести сантиметр как мерку для из­мерения небольших отрезков, длина которых меньше метра.

Чтобы дети получили наглядное представление о сантимет­ре, следует выполнить ряд упражнений. Например, полезно, что­бы они сами изготовили модели сантиметра (нарезали из узкой полоски бумаги в клетку полоски длиной 1 см), начертили от­резки длиной 1 см в тетрадях (по клеточкам), нашли, что ши­рина мизинца примерно равна 1 см.

Далее учащихся знакомят с измерением отрезков. Чтобы дети ясно поняли процесс измерения и что показывают числа, получаемые при измерении, целесообразно постепенно перехо­дить от простейшего приема укладывания моделей сантиметра и их подсчета к более трудному — отмериванию («прошагать» меркой по отрезку и подсчитать, сколько раз отложилась еди­ница измерения). Только затем приступать к измерению спосо­бом прикладывания линейки или рулетки к измеряемому отрезку.

Многие методисты советуют сначала пользоваться линейками, которые изготовляются детьми из листа бумаги в клеточку. На этих ли­нейках наносятся сантиметровые деления, но цифры не пишут­ся. Пользуясь этими линейками, дети измеряют отрезки, чертят отрезки на нелинованной бумаге, показывают отрезки заданной длины на самой линейке. При этом каждый раз дети подсчиты­вают сантиметры (прошагивая» их карандашом). Чем больше упражнений выполнят учащиеся, пользуясь самодельными ли­нейками, тем успешнее овладевают они умением измерять с по­мощью обычной масштабной линейки.

При работе с масштабной линейкой обращается внимание на правильность положения линейки при измерении (начало от­резка должно совпадать с нулевым делением на линейке). Сле­дует научить детей выполнять округление результатов измере­ния: если сантиметр уложился 5 раз и остался отрезок, мень­ше половины сантиметра, то его отбрасывают и называют дли­ну отрезка так: «немного больше 5 см», «около 5 см»; если ос­тался отрезок, который равен половине сантиметра или больше, то его засчитывают за целый сантиметр и результат измерения называют так: «немного меньше 6 см», «приблизительно 6 см». Для формирования измерительных навыков включается си­стема разнообразных упражнений. Это измерение и черчение отрезков; сравнение отрезков, чтобы ответить на вопрос: на скольку сантиметров длиннее (короче) один отрезок, чем дру­гой; увеличение и уменьшение их на несколько сантиметров. В процессе этих упражнений у учащихся формируется понятие длины как числа сантиметров, которые укладываются в данном отрезке.

Позднее, при изучении нумерации чисел в пределах 100, вводится новая единица измерения — дециметр. Работа проходит в таком же плане, как и при знакомстве с сан­тиметром. Затем устанавливают отношения между единицами измерения (сколько сантиметров содержится в 1 дм). Дети упражняются в измерении с помощью двух разных мерок (например, длина крышки парты 4 дм 5 см, длина доски 2 м 8 дм). С этого времени приступа­ют к сравнению длин на основе сравнения соответствующих отрезков.

Затем рассматривают преобразования величин: замену круп­ных единиц мелкими (3 дм 5 см = 35 см) и мелких единиц крупными (48 см = 4 дм 8 см). Постепенно учащиеся осознают, что числовое значение длины зависит от выбора единицы из­мерения (например, длина одного и того же отрезка может быть обозначена и как 3 дм, и как 30 см).

Сравнение двух длин, выраженных в единицах двух наиме­нований, теперь выполняют на основе преобразования их и сравнения числовых значений, при которых стоят одинаковые наименования единиц измерения (4 дм 8 см>39 см, так как 48 см>39 см, или 4 дм 8 см>3 дм 9 см).

Во III классе знакомство с единицами длины продолжается: дети знакомятся с метром, миллиметром, а позднее с километром. Процессе формирования представлений о метре начинается с предъявления соответствующей модели, затем соответствующая протяженность измеряется и аналитически устанавливаются отношения между единицами измерения (сколько сантиметров содержится в 1 м, сколько дециметров в 1 м).

Введение миллиметра обосновывается необходимостью измерять отрезки, меньшие 1 см. Наглядное представление о миллиметре дети получают, рассматривая деление на обычной масштабной линейке или на миллиметровой бумаге. Сразу же устанавливается, сколько миллиметров содержится в 1 см, и дети приступают к измерениям с точностью до миллиметра (с помощью циркуля, а также с помощью линейки). При этом особое внимание обращается на то, чтобы дети правильно рас­полагали глаз при совмещении концов отрезка с делениями на шкале линейки. Для формирования измерительных навыков включаются упражнения на измерения не только на уроках ма­тематики, но и на других уроках (например, чертежи на уроках труда тоже должны выполняться с точностью до миллиметра).

Для развития глазомера полезно, прежде чем измерять за­данные отрезки (в учебнике, на карточках), прикинуть на глаз их длину. Хорошим средством закрепления измерительных графических и вычислительных навыков являются задачи на измерение и вычисление периметра геометрических фигур, уп­ражнения в построении отрезков и прямоугольников.

При знакомстве с километром полезно провести практи­ческие работы на местности, чтобы сформировать представле­ние об этой единице измерения. Чаще всего дети вместе с учи­телем проходят расстояние, равное 1 км (или 500 м) (полезно заметить время, за которое удалось пройти это расстояние). Измеряют пройденное расстояние либо шагами (2 шага при­мерно составляют 1 м), либо с помощью рулетки или мерной веревки. Попутно дети упражняются в определении некоторых расстояний на глаз. Если есть возможность, проводят экскур­сию на автобусный или железнодорожный вокзал, чтобы уз­нать данные о расстояниях до ближайших населенных пунк­тов и городов. Этот материал потом используется на уроках при составлении задач.

В IV классе учащиеся составляют и заучивают таблицу всех изученных единиц длины и их отношений. Таблица усваива­ется в процессе многократных и систематических упражнений вида: сколько метров в 1 км? Во сколько раз метр больше де­циметра? На сколько сантиметров 1 м больше, чем 1 см? Сколько метров составляет половина километра? четверть километ­ра? десятая часть километра? и т.п. Кроме того, продолжается работа по преобразованию и сравнению длин, выраженных в единицах двух наименований, изучаются письменные приемы вычислений над ними.

Начиная со II класса дети в процессе решения задач зна­комятся с нахождением длины косвенным путем. Например, зная длину одного класса и число классов на одном этаже, вычис­ляют длину здания школы; зная высоту комнат и количество этажей дома, можно вычислить приблизительно высоту дома и т п. Позднее, после ознакомления со скоростью движения и изучения связи между величинами скорость — вре­мя — расстояние учащиеся узнают о том, что можно вычислять расстояния, зная скорость и время движения (например, длину воздушных и морских линий, расстояния, пройденные косми­ческими кораблями, спутниками, и т.п.).

Работу над этой темой полезно продолжить на внеклассных занятиях, например: рассмотреть старинные и нестандартные меры (вер­ста, сажень, вершок, фут, дюйм и др.), ознакомить учащихся с некоторыми сведениями из истории развития системы мер длины.
Площадь геометрической фигуры

В методике работы над площадью фигуры имеется много общего с работой над длиной отрезка.

Прежде всего, площадь выделяется как свойство плоских предметов среди других их свойств, т.е. это место, занимаемое плоскими предметами на плоскости стола, пола и т.п.. Уже дошкольники сравни­вают предметы по площади (не называя само слово «площадь») и правильно устанавливают отношения «больше», «меньше», «равно» («одинаково»), если сравниваемые предметы очень резко отличаются друг от друга или совершенно одинаковые. При этом дети пользуются наложением предметов или срав­нивают их на глаз, сопоставляя предметы по занимаемому мес­ту на столе, на земле, на листе бумаги и т.п. Например, лист березы меньше, чем лист клена, каток у школы больше, чем у нашего дома, все блины одинаковые — не больше и не мень­ше и т.п. Однако, сравнивая предметы, у которых форма раз­лична, а различие площадей не очень четко выражено, дети ис­пытывают затруднения. В этом случае они заменяют сравнение по площади сравнением по длине или по ширине предметов, т.е. переходят на линейную протяженность, особенно в тех случаях, когда по одному из измерений предметы сильно отличаются друг от друга.

В процессе изучения геометрического материала у детей уточняются представления о площади как о свойстве плоских геометрических фигур. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади. Этому способствуют упражнения на вырезывание фигур из бумаги, черчение и раскрашивание их в тетрадях и т.п. В процессе решения задач с геометрическим содержанием (например, составление фигур из заданных час­тей, вычленение различных фигур на сложном чертеже и т.п.) учащиеся знакомятся с некоторыми свойствами площади. Они убеждаются, что площадь не изменяется при изменении поло­жения фигуры на плоскости (фигура не становится ни больше, ни меньше). Дети многократно наблюдают соотношение между всей фигурой и ее частями (часть меньше целого), упражняются в составлении различных по форме фигур из одних и тех же за­данных частей (т.е. построении равносоставленных фигур). Учащиеся постепенно накапливают представления о делении фигур на неравные и равные части, сравнивая наложением по­лученные части (например, во II классе при изучении долей). Все эти знания и умения дети приобретают практическим пу­тем попутно с изучением самих фигур. Важно, чтобы учитель обращал внимание детей на эти вопросы и тем самым подготав­ливал учащихся к изучению в IV классе площади фигур.

Ознакомление с площадью можно провести так: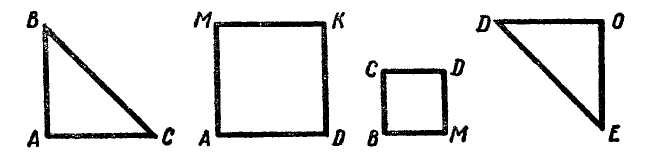

«
Посмотрите на фигуры, прикрепленные к доске (рис. 1) и скажите, какая из них занимает больше всех места на доске (квадрат AMKDзанимает места больше всех фигур). В этом случае говорят, что площадь квадрата больше, чем площадь каждого треугольника и квадрата CDMB. Сравните площадь треугольника ABCи квадрата AMKD(площадь треугольника меньше, чем площадь квадрата). Посмотрите, я сравню эти фи­гуры наложением — треугольник занимает только часть квадра­та, значит, действительно площадь его меньше площади квад­рата. Сравните на глаз площадь треугольника ABCи площадь треугольника DOE(у них площади одинаковые, они занимают одинаковое место на доске, хотя расположены по-разному). Проверьте наложением».

Аналогично сравниваются по площади другие фигуры, а так­же предметы окружающей обстановки.

Затем для сравнения предлагают фигуры, одну из которых невозможно полностью поместить на другую, но площадь первой фигуры очевидно меньше площади второй фигуры: например прямоугольник 2×30 см и квадрат 15×15 см. В процессе поиска решения возникшей проблемной ситуации ученики приходят к выводу: первую фигуру следует разделить на части, которые можно полностью наложить на вторую фигуру.

Затем демонстрируется, что не всегда так легко установить, какая из двух фи­гур имеет большую (меньшую) площадь или они одинаковы по площади. Чтобы показать это учащимся, можно предложить им сравнить вырезанные из бумаги прямоугольник и квадрат, не­значительно отличающиеся по площади, например: размеры квадрата 4×4 дм, а прямоугольника 5×3 дм, при этом фигу­ры с обратной стороны разбиты на квадратные дециметры. Сна­чала учащиеся пытаются сравнить эти фигуры на глаз, а так­же путем наложения. Однако оба способа не помогают детям решить вопрос убедительно. Выслушав различные предположе­ния, учитель поворачивает фигуры той стороной, на которой сделана разбивка на квадраты, и предлагает сосчитать, сколь­ко одинаковых квадратов содержит каждая фигура. На этой основе дети устанавливают, площадь какой фигуры больше, а какой — меньше. Аналогичные упражнения на сравнение пло­щади фигур, составленных из одинаковых квадратов, выпол­няются по учебнику, а также по чертежам, данным на доске. Дети убеждаются в том, что если фигуры состоят из одинако­вых квадратов, то площадь той фигуры больше (меньше), ко­торая содержит больше (меньше) квадратов. Полезно на этом же уроке рассмотреть такой случай, когда разные по форме фигуры имеют одинаковую площадь, так как содержат одина­ковое число квадратов (например, квадрат —16 кв. ед. и прямо­угольник — 16 кв. ед.). На последующих уроках включаются уп­ражнения на подсчет квадратов, содержащихся в заданных фи­гурах, предлагается начертить в тетрадях фигуры, которые со­стоят из заданного числа квадратов (клеточек тетради). В про­цессе таких упражнений начинает формироваться понятие о площади как о числе квадратных единиц, содержащихся в гео­метрической фигуре.

Н 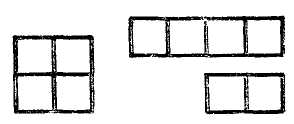а следующем этапе учащихся знакомят с первой единицей площади — квадратным сантиметром. Учащиеся чертят в тетра­дях, вырезают из бумаги в клеточку квадраты со стороной 1 см. Учитель сообщает: «Это единица площади — квадратный санти­метр». Используя бумажные модели квадратного сантиметра, дети составляют из них различные геометрические фигуры и находят подсчетом их площадь (рис. 2). Сравнивая площади составленных фигур, дети еще раз убеждаются, что площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратных сантиметров. Площади фигур, содержащих одина­ковое число квадратных сантиметров, равны, хотя фигуры мо­гут не совмещаться при наложении. Эффективен на этом этапе прием сопоставления знакомых де­тям величин — длины отрезка и площади фигуры, который помога­ет предупредить смещение этих ве­личин. Выполняя конкретные уп­ражнения, обнаруживают некоторое сходство и существенное различие этих величин: сантиметр — единица длины; квадратный санти­метр— единица площади; длина отрезка — число сантиметров, которые содержатся в данном отрезке; площадь фигуры — чис­ло квадратных сантиметров, содержащихся в этой фигуре (рис. 3).

В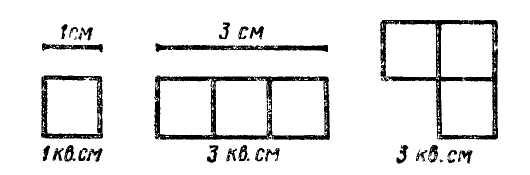
дальнейшем наглядное представление о квадратном сан­тиметре и понятие о площади фигур закрепляются. Включают­ся упражнения на нахождение площади фигур, разбитых на квадратные сантиметры. Предлагается при подсчете квадратных сантиметров группировать их по рядам или столбцам, чтобы ускорить нахождение их общего числа. Рассматриваются и та­кие фигуры, которые наряду с целыми квадратными сантимет­рами содержат и нецелые — половины, а также доли больше или меньше, чем половина квадратного сантиметра (рис. 4). Следует также ознакомить учащихся с нахождением прибли­женной площади фигуры таким способом: сосчитать все неце­лые квадратные сантиметры и общее число их разделить на два, затем полученное число сложить с числом целых квадрат­ных сантиметров, которые содержатся в данной фигуре.

Д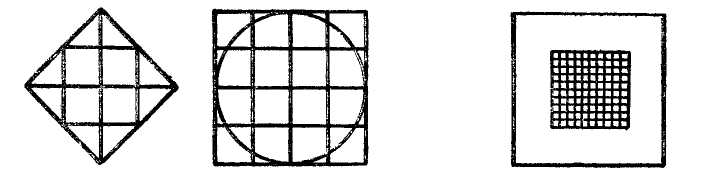
ля нахождения площади геометрических фигур, не разде­ленных на квадратные сантиметры, используют палетку. Па­летка — это прозрачная пластинка, разбитая на равные квад­раты. Сетка может быть нанесена на кальку или состоять из нитей, натянутых на рамку. На данном этапе используют палет­ку, каждое деление которой равно квадратному сантиметру. Полезно такую палетку изготовить с детьми на уроке труда. Наложив палетку на геометрическую фигуру, под­считывают число целых и нецелых квадратных сантиметров, которые в ней содержатся. Для нахождения площади фигур, начерченных в тетрадях, в качестве палетки используют разли­новку тетрадей. Каждый раз подчеркивают, что найденная пло­щадь равна приблизительно такому-то числу (около 20 кв. см, приблизительно 15 кв. см).

В это же время приступают к сопоставлению площади и пе­риметра многоугольников с тем, чтобы дети не смешивали эти понятия, а в дальнейшем четко различали способы нахождения площади и периметра прямоугольника. Выполняя практические упражнения с геометрическими фигурами, дети подсчитывают число квадратных сантиметров и тут же измеряют периметр многоугольника в сантиметрах.

На следующем этапе учащиеся знакомятся с приемом вы­числения площади прямоугольника (квадрата). Сначала рас­сматривают прямоугольники, которые уже разделены на квад­ратные сантиметры. Их площадь находят путем подсчета квад­ратных сантиметров в одном ряду, а затем полученное число умножают на число рядов. Например, если в одном ряду 6 кв. см, а таких рядов 5, то площадь равна 6 · 5, т.е. 30 кв. см. Очень важно при этом установить соответствие между длиной прямо­угольника и числом квадратных сантиметров, прилегающих к длине; шириной прямоугольника и числом рядов. Например, если в ряду 6 кв. см, то длина прямоугольника 6 см, а если рядов 5, то ширина прямоугольника 5 см.

Затем дети чертят прямоугольник по заданным длинам сто­рон, разбивают его на ряды, а один ряд на квадраты и снова убеждаются в соответствии: если длина 4 см, то в одном ряду, прилегающем к этой стороне, содержится 4 кв. см, если ширина 3 см, то таких рядов оказывается 3. Число квадратных санти­метров равно произведению чисел 4 и 3 (рис. 5). Делается вывод: чтобы вычислить площадь прямоугольника, нужно знать его длину и ширину (в одинаковых единицах) и найти произ­ведение этих чисел.

Сравнив разные способы нахождения площади, дети сами могут решить вопрос, что легче: измерить длину и ширину прямоугольника и полученные числа перемножить или разбить прямоугольник на квадратные сантиметры и сосчитать их.

Д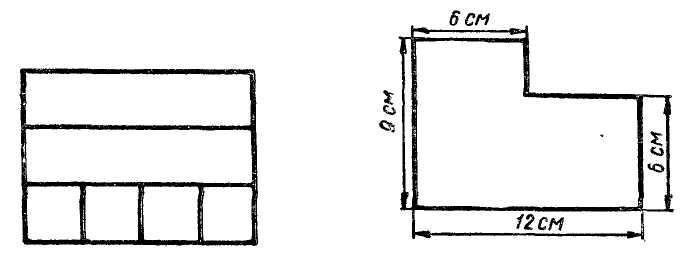
алее включаются устные и письменные задания на вычис­ление площади прямоугольников (квадратов) и периметров этих фигур. Очень полезны упражнения в вычислении площади и пе­риметра фигур, составленных из нескольких прямоугольников. Здесь учащимся приходится вычислять площади каж­дого прямоугольника, а затем находить их сумму, т.е. площадь заданной фигуры.

В процессе решения задач на вычисление площади и пери­метра прямоугольников следует показать, что фигуры, имею­щие одинаковую площадь, могут иметь неодинаковые перимет­ры, и что фигуры, имеющие одинаковые периметры, могут иметь неодинаковые площади. Например, это легко наблюдать при за­полнении таблицы вида:

Длина	7 см	6 см	5 см	4 см
Ширина	1 см	2 см	3 см	4 см
Периметр	16 см	16 см	16 см	16 см
Площадь	7 кв. см	12 кв. см	15 кв. см	16 кв. см

По таблице учащиеся чертят прямоугольники указанных раз­меров, вычисляют площадь и периметр и записывают их в таб­лицу. Наглядные иллюстрации помогают детям осознать на­блюдаемые соотношения. Легко подметить, что наибольшую площадь при одинаковом периметре имеют прямоугольники с равными сторонами (квадраты). Аналогичную работу можно провести по наблюдению изменения периметра в зависимости от изменения длины сторон при одинаковой площади (например, прямоугольники со сторонами 12 см и 2 см, 8 см и 3 см, 6 см и 4 см).

Далее учащиеся знакомятся с квадратным дециметром. Как и при введении квадратного сантиметра, прежде всего форми­руется наглядный образ новой единицы: дети чертят на клет­чатой бумаге квадрат со стороной 1 дм и затем вырезают его, составляют фигуры из нескольких квадратных дециметров, на­зывая их площадь и периметр. Устанавливается отношение меж­ду квадратным дециметром и квадратным сантиметром. Уча­щиеся сами вычисляют площадь квадрата со стороной 1 дм в квадратных сантиметрах и записывают: 1 кв. дм=100 кв.см. Затем дети учатся заменять мелкие единицы крупными и на­оборот. Решаются задачи на вычисление площади прямоуголь­ников (квадратов) и фигур, составленных из прямоугольников, стороны которых заданы в дециметрах либо в дециметрах и сантиметрах.

На следующем этапе аналогично рассматривается квадрат­ный метр. Обращается особое внимание на решение практиче­ских задач: измерение и вычисление площади пола в классе, коридоре, комнате, сравнение площадей помещений, имеющих одинаковую, положим, ширину и различную длину.

Наряду с решением задач на нахождение площади прямо­угольника по данным длине и ширине решают обратные зада­чи на нахождение одной из сторон по известной площади и другой стороне прямоугольника. Площадь — это произведение чисел, полученных при измерении длины и ширины прямоуголь­ника, значит, нахождение одной из сторон прямоугольника сво­дится к нахождению одного из множителей по произведению и другому множителю. Кроме простых задач, решаются и со­ставные задачи, в которых наряду с площадью включается пе­риметр, например: «Огород имеет форму квадрата, периметр которого 320 м. Чему равна площадь огорода?»
Масса

Первые представления о том, что предметы имеют массу, дети получают в жизненной практике до школы. Взяв в руки предметы, дети на основе ощущений устанавливают, какой предмет тяжелее, какой легче или по массе они одинаковы. Однако чувственный опыт дошкольников недостаточно велик, поэтому сравнить массу двух предметов на руку дети могут лишь в том случае, если предметы по данному свойству очень отличаются друг от друга, а по другим свойствам сходны. Сильное влияние на оценку массы оказывают размеры пред­мета (большой по объему предмет кажется им всегда большим по массе).

В процессе изучения первого десятка необходимо наряду с непосредственным сравнением предметов по длине (ширине, вы­соте) предлагать одновременно сравнивать предметы по мас­се. Чтобы помочь детям выделить массу среди других свойств, следует для сравнения давать предметы, имеющие различную массу, но сходные по другим свойствам (например, два оди­наковых по размерам кубика: один пластмассовый, другой ме­таллический). Во II классе формируются представления об устройстве рычажных весов и формируется умение сравнивать массу предметов с их помощью.

В III классе дети знакомятся с первой единицей массы — кило­граммом. Подвести детей к пониманию необходимости измерять массу можно ссылкой на измерение длины, с чем уже знакомы дети. Учитель приносит на урок несколько предметов, масса каждого из которых равна килограмму (пачка соли, мешочек с горохом, пакет с крупой и т.п.). Чтобы сформировать конкрет­ные представления о массе в 1 кг, детям дают подержать в руках предметы с такой массой и сравнить их с предметами, которые тяжелее или легче их. Когда дети отберут 2–3 пред­мета одинаковой массы, учитель сообщает, что каждый пред­мет имеет массу в один килограмм — такую же, как и кило­граммовая гиря (гирю тоже предлагают подержать в руках каждому ученику).

Далее с помощью весов иллюстрируют то, что каждый из отобранных предметов массой в 1 кг, а другие предметы — боль­ше или меньше килограмма. Учитель показывает, как пользо­ваться для этого весами.

Затем выполняются упражнения в отвешивании: отве­шивают 1, 2, 3 кг соли, крупы и т.п. Дети должны активно участвовать в работе с весами; например, один ученик ставит гири на левую чашку весов, другой насыпает крупу на правую чашку весов. Остальных детей привлекают к пояснению про­цесса взвешивания (что перевешивает; что надо сделать, что­бы весы пришли в равновесие; сколько килограммов крупы, со­ли взвешено и т.п.). Попутно происходит знакомство с записью полученных результатов. Полезно при отвешивании 1 кг ово­щей подсчитать (и записать), сколько штук картофеля (лука, моркови и т.п.) идет на килограмм.

Дети знакомятся с набором гирь (1 кг, 2 кг, 5 кг) и затем приступают к взвешиванию нескольких специально подо­бранных предметов, масса которых выражается целым числом килограммов. Здесь сначала устанавливается на весах груз, а потом подбираются гири. Полученные величины используются для составления задач.

В дальнейшем для развития у детей умения оценивать мас­су на глаз и на руку ученикам предлагают перед взвешивани­ем попытаться прикинуть — больше или меньше килограмма масса этого груза, а затем уже проверить это с помощью взве­шивания. Полезно дать детям задание узнать, какова масса часто встречающихся в быту предметов, таких, как буханка хлеба, литр молока, ведро картофеля и т.п. Эти данные также используются при составлении задач детьми. Следует включать решение задач, которые воспроизводят процесс взвешивания, например: «На одной чашке весов стоит ящик с яблоками, на другой — две гири по 5 кг. Весы находятся в равновесии. Ка­кова масса яблок, если масса пустого ящика 1 кг?» Такие за­дачи вооружают детей практическими сведениями (учет тары при взвешивании).

Следующая единица мас­сы — грамм. Название его известно учащимся. Задача учи­теля— сформировать наглядное представление о грамме. С этой целью детям дают подержать гирьку в 1 г, а также взвешивают старые советские монеты и устанавливают, что масса монеты в 1 коп. — 1 г, 2 коп. — 2 г, 3 коп. — 3 г, 5 коп. — 5 г. Дети знакомятся с набо­ром гирь, меньших килограмма, с помощью весов убеждаются, что 1 кг равен 1000 г. Затем приступают к упражнениям в от­вешивании с точностью до грамма. Запись полученных масс (460 г, 900 г, 125 г и т.п.), их чтение, сравнение помогает де­тям усваивать нумерацию чисел в пределах 1000.

Рекомендуется у учащихся сформировать представления о различных видах весов (ци­ферблатных автоматических, электронных): рассмотреть шкалу, научиться отсчитывать деления на шкале и читать ее показания, освоить процесс взвешивания на таких весах. Полезно провести экскурсию в ближайший продовольственный магазин и пона­блюдать работу на таких весах: посмотреть, как устанавливают циферблатные весы перед взвешиванием, как взвешивают гру­зы больше 1 кг; убедиться, как важно, читая показания шка­лы при взвешивании, смотреть на нее прямо, а не сбоку.

В IV классе учащиеся знакомятся с новыми единицами массы — центнером и тонной, устанавливаются их отношения с килограммом, составляется и заучивается таблица единиц массы. Чтобы дать конкретные представления о новых единицах мас­сы, используют рисунки и иллюстрированные таблицы единиц массы (например, 2 мешка сахарного песку имеют массу 1 ц, масса легкового автомобиля без пассажиров — примерно 1 т и т.п.). Если есть возможность, надо ознакомить детей с ве­сами, на которых взвешиваются тяжелые предметы с массой в несколько центнеров или тонн, провести экскурсию на склад или базу.

На данном этапе приступают к преобразованию величии, вы­раженных в единицах массы (заменяя мелкие единицы круп­ными и обратно), а также сравнивают массы и выполняют арифметические действия над ними. В процессе этих упражне­ний закрепляются знания таблицы единиц массы.

Начиная со III класса в процессе решения простых, а затем составных задач учащиеся устанавливают и используют вза­имосвязь между величинами: масса одного предмета — количе­ство предметов — их общая масса, учатся вычислять каждую из величин, если известны значения двух других.
Время

Вся жизнь человека тесно связана со временем, с умением измерять, распределять, ценить время. Время течет непрерывно, его нельзя ни остановить, ни возвратить, поэтому восприятие промежутков времени, сравнение событий по продолжительно­сти очень затруднено. Как известно, наше восприятие времени несовершенно: нам кажется, что время течет то быстрее, то медленнее в зависимости от того, чем заполнен тот или иной промежуток времени. Поэтому время — одна из трудных для изучения величин. Временные представления у детей развива­ются медленно, в процессе длительных наблюдений, накопления жизненного опыта, изучения других величин.

Первые представления о времени де­ти получают в дошкольный период. Сме­на дня и ночи, смена времен года, повто­ряемость режимных моментов в жизни ребенка — все это формирует временные представления. Однако как временная последовательность событий (что было раньше, что позже), так и особенно представление о продолжительности со­бытий усваиваются детьми с большим трудом. Типичными являются ошибки детей в установлении последовательности событий (например, дети смешивают понятия «вчера» и «завтра»).

Временные представления у первоклассников формируются, как и у дошкольников, прежде всего в процессе их практиче­ской (учебной) деятельности: режим дня, ведение календаря природы, восприятие последовательности событий при чтении сказок, рассказов, при просмотре кинофильмов, ежедневная запись в тетрадях даты работы — все это помогает ребенку уви­деть изменения времени, почувствовать течение времени.

Программа предусматривает в I классе знакомство детей с названиями дней недели и их последовательностью. В качест­ве наглядного пособия полезно иметь в классе отрывной кален­дарь или модель настольного календаря (рис. 69), работать с которым надо научить детей.

Начиная с I класса необходимо приступить к сравнению знакомых, часто встречающихся в опыте детей временных про­межутков. Например, что длится дольше: урок или перемена, учебная четверть или зимние каникулы, что короче по времени: занятия ученика в школе или рабочий день родителей? Такие задания способствуют развитию чувства времени. В процессе решения задач, связанных с понятием разности, дети присту­пают к сравнению возраста людей и постепенно овладевают важными понятиями старше — моложе — одинаковые по воз­расту.

Ввиду большой практической потребности полезно ознако­мить первоклассников с тем, как по часам определяется время, при этом достаточно, если дети научатся пока вести отсчет вре­мени с точностью до часа.

Знакомство с единицами времени способствует уточнению временных представлений детей. Знание количественных отно­шений единиц времени помогает сравнивать и оценивать по продолжительности промежутки времени, выраженные в тех или иных единицах. Также в I классе изучаются такие единицы времени, как месяц и год. Сутки и час изучаются во II классе, минута и секунда — в III классе, а век (столетие) — в IV классе. Необходимо формировать у детей конкретные представления о каждой единице времени, добиваться усвоения их отношений, научить пользоваться календарем и часами и с их помощью решать несложные задачи на вычисление продол­жительности события, если известны его начало и конец, а так­же задачи, обратные данной (т.е. на установление начала и концасобытия).

Чтобы подготовить детей к восприятию единиц времени, не­обходимо во II классе продолжать систематическую работу с календарем, начатую в I классе. Подводя итоги и обобщая на­блюдения, полезно обращать внимание детей на последова­тельность месяцев и количество дней в каждом месяце. При записи даты в тетрадях следует также почаще задавать вопро­сы на выяснение последовательности месяцев. (Сегодня 1 ок­тября. А предыдущий месяц как назывался? Какой следующий месяц после октября? и т.п.)

Знакомя детей с месяцем и годом, учитель использу­ет табель-календарь. По нему дети выписывают названия ме­сяцев по порядку и количество дней в каждом месяце. Сразу же выделяют одинаковые по продолжительности месяцы, отме­чают самый короткий месяц в году — февраль (28 или 29дней). По календарю учащиеся определяют порядковый номер меся­ца (Как называется пятый месяц в году? Которым по счету является июль? и т.п.), устанавливают день недели, если из­вестно число и месяц, и наоборот, устанавливают, на какие числа месяца приходятся определенные дни недели (В какой день недели будет праздник 8 Марта в этом году? На какие числа приходятся воскресенья в марте? и т.п.).

С помощью календаря учащиеся решают задачи на нахож­дение продолжительности события (в пределах одного года). Например, сколько дней длились весенние каникулы? Сколько месяцев длятся летние каникулы? Учитель называет начало и конец каникул, и учащиеся подсчитывают число дней и меся­цев по календарю. Надо показать, как быстро подсчитать чис­ло дней, зная, что в неделе 7 дней. Аналогично решаются об­ратные задачи.

Понятие о сутках раскрывается через близкие детям по­нятия о частях суток — утро, день, вечер, ночь (или день с утра до вечера и ночь). Кроме того, опираются на представле­ние временной последовательности: вчера, сегодня, завтра. Детям предлагают перечислить, чем они были заняты от вче­рашнего утра до сегодняшнего утра, что будут делать начиная с сегодняшнего вечера и до завтрашнего вечера и т.п. «Такие промежутки времени,— сообщает учитель,— называют сутка­ми». Дети устанавливают, сколько суток проходит со вчераш­него вечера до завтрашнего вечера (от позавчерашнего утра до послезавтрашнего утра и т.п.), сколько суток прошло от начала недели (понедельника) до субботы, которые по счету сутки наступят, объясняют пословицу: «День и ночь — сутки прочь». Далее можно провести аналогичную работу по календарю: сколько полных суток прошло от начала месяца до сегодняшнего дня, которые по счету сутки наступили? Чтобы установить связь с изученными единицами времени, можно предложить задания на сравнение: «Что дольше длится: 5 суток или неделя, 20 суток или 1 месяц?» и т.п.

Следующими рассматриваются час и минута. Конкрет­ные представления о соответствующих промежутках времени также формируются через практическую деятельность детей, через наблюдения. Так, час — это примерно продолжительность одного урока и перемены. Чтобы ощутить время продолжитель­ностью в 1 мин, включают упражнения, с помощью которых де­ти узнают, что можно успеть сделать за 1 мин (до какого чис­ла успеешь сосчитать, сколько можно решить примеров, какое расстояние пройти и т.п.). Уместно здесь объяснить смысл по­словицы: «Минута час бережет».

Большое воспитательное значение имеют примеры из жизни нашей страны, числовые данные о том, сколько продукции за­воды и фабрики выпускают за 1 мин, за 1 ч, за 1 рабочий день.

На первом же уроке по знакомству с часом и минутой со­общаются отношения между мерами времени: в 1 сутках 24 ча­са, в 1 часе 60 минут. Для закрепления включают упражнения вида: «Сколько часов составляют двое (трое, четверо) суток? Сколько минут составляет половина часа (треть часа; четверть часа и т.п.)?»

Важным моментом на данном этапе является знакомство с циферблатными часами. Чтобы дети научились устанавливать время по часам, полезно заблаговременно изготовить с учащимися на уроках труда циферблат с подвижными стрелками и, используя эту модель часов, выполнять практические упражнения. Учащиеся вспоминают, с какими часами они знакомы, сталкивались в жизни. Учитель поясняет, что все часы устроены таким обра­зом, что, пока большая стрелка движется от одного маленького деления до другого, проходит 1 минута, а пока маленькая стрелка движется от одного большого деления до другого, про­ходит 1 час. Счет времени ведется от полуночи до полудня (12 ч дня) и от полудня до полуночи. Затем предлагаются уп­ражнения с использованием модели часов: назвать обозначен­ное время и обозначить время, которое называет учитель или сами ученики. Даются разные формы чтения показаний часов, например: 9 часов 30 минут, 30 минут десятого, половина деся­того; 4 часа 45 минут, 45 минут пятого, без 15 минут пять, без четверти пять и т.п. С помощью модели часов решаются зада­чи, на определение продолжительности события, начала или конца его (в пределах одних суток).

Усвоению отношений между единицами времени помогает таблица мер, которую следует повесить в классе на некоторое время, а также систематические упражнения в преобразовании величин, выраженных в единицах времени (сколько минут составляет 1 час и 30 минут, сколько суток составляет 72 часа и т.п.), их сравнении, нахождении различных долей любой еди­ницы времени, решение задач на вычисление времени.

Далее таблица единиц времени пополняется — учащиеся знакомятся с секундой и веком. Конкретное пред­ставление о продолжительности секунды дети получают на ос­нове наблюдения (устанавливают, что можно сделать за 1 с, 5 с, 10 с).

Век — самая крупная из рассматриваемых единиц времени. Некоторое представление о продолжительности отрезка време­ни в 100 лет дети могут получить, сравнивая свой возраст, воз­раст близких людей, «возраст» нашего государства с веком. Можно для наглядности начертить соответствующие отрезки на бумаге, используя масштаб.

Знания о системе единиц времени расширяются. Дети уз­нают на уроках природоведения, что сутки — время, в течение которого Земля делает полный оборот вокруг своей оси, и год — время, в течение которого Земля делает полный оборот вокруг Солнца. Учащиеся под руководством учителя составляют таб­лицу единиц времени, а затем в процессе разнообразных уп­ражнений усваивают ее.

В III–IV классах рассматривают простейшие случаи сложения и вычитания величин, выраженных в единицах времени. Необ­ходимые преобразования единиц времени здесь выполняют по­путно, без предварительной замены заданных величин. Чтобы предупредить ошибки в вычислениях, которые намного слож­нее, чем вычисления с величинами, выраженными в единицах длины и массы, рекомендуется чаще давать вычисления в сопо­ставлении:

_30 мин 45 с _30 м 45 см _30 ц 45 кг

20 мин 58 с 20 м 58 см 20 ц 58 кг
Так же для развития временных пред­ставлений используется решение задач на вычисление продол­жительности события, его начала и конца. Простейшие задачи на вычисление времени в пределах года (месяца) решаются с помощью табеля-календаря, а в пределах одних суток — с по­мощью модели часов.

Ч
етвероклассники знакомятся с 24-часовым счислением вре­мени суток. Они узнают, что началом суток является полночь (0 ч), что счет часов в течение суток идет от начала суток, поэтому после полудня (12 ч) каждый час имеет другой поряд­ковый номер (1 час дня — это 13 ч, 2 часа дня— 14 ч и т.д.).
Усвоению этой системы отсчета помогает изображение ее с помощью отрезка. При решении задач, связанных с вычисле­нием времени, учащиеся также пользуются этой иллюстрацией.

Аналогично изображают отрезками на прямой века (столе­тия). Пользуясь такой «лентой времени», третьеклассники ус­танавливают, в каком веке произошло то или иное историче­ское событие, в каком веке мы живем, в каком году начнется 21 век и т.п. Это наряду с формированием временных представ­лений подготавливает детей к изучению истории в средней шко­ле, формирует начатки исторических представлений.

В связи с изучением данной темы в полезно про­вести внеклассное занятие, на котором поставить задачу — расширить знания детей о времени и его измерении, пробудить интерес у учащихся к этому материалу. Это могут быть рас­сказы о том, как человек измерял время в далеком прошлом, о первых календарях и часах и др.