Попопать. Практическое занятие 7. Методика изучения вычислительных приемов в концентре Числа от 1 до 100

• Название: Методика изучения вычислительных приемов в концентре Числа от 1 до 100
• Анкор: Попопать
• Дата: 30.11.2021
• Размер: 1.47 Mb.
• Имя файла: Практическое занятие 7.docx
• Тип: Урок; #286551

Практическое занятие 7.

Тема: «Методика изучения вычислительных приемов в концентре

«Числа от 1 до 100»»

Задания для самоподготовки.
1. Прочитайте описание двух первых уроков по теме «Двузначные числа».

Ответьте на следующие вопросы:


1) Какой из конспектов выбрали бы вы, если бы проводили этот же урок? Почему?


2) По одной или по разным программам работают эти учителя? Почему вы так думаете?


3) Отличаются ли приведенные конспекты по содержанию?

4) Какие методы используются на одном и другом уроке для знакомства учащихся с новой счетной единицей — десятком (репродуктивные, частично-поисковые, проблемные)?


5) Какую функцию выполняют на одном и другом уроке предметные модели (иллюстративную, познавательную)?

6) Какие методические приемы используются на каждом уроке для активизации мыслительной деятельности школьников (анализ, сравнение, аналогия, обобщение)?


7) Какие методические приемы используются на одном и другом уроке для постановки учебной задачи?

Урок 1

Учитель предлагает каждому ученику отсчитать 10 палочек и связать их в пучок.

– Это 1 десяток, – говорит он.

– Кто знает, как записать число десять? (Большинство детей самостоятельно записывают в тетрадях число 10).

– А теперь посчитайте круги, которые вы видите на доске. (15 – 20 кругов). (Большинство детей справляются с заданием учителя).

– Как же записать цифрами числа одиннадцать, двенадцать и т.д.? – спрашивает учитель и записывает на доске слова числительные – одиннадцать, двенадцать, тринадцать и т.д., выделяя красным цветом подчеркнутые части слов-числительных.

Затем учитель помещает на доске несколько карточек с числом 10, произносит названия двузначных чисел и закрывает в каждом числе 10 цифру 0 сначала цифрой 1 (на карточке получается 11), затем цифрой 2 (12), цифрой 3 (13) и т. д.

– Запишите полученные числа в тетрадях. (Дети выполняют задание учителя).

– Можно ли назвать эти числа однозначными? (Нет, они записаны двумя знаками).

– Посмотрите, как можно записать каждое получившееся число в виде суммы двух слагаемых (записывает на доске: 10 + 1 = 11; 10 + 2 = 12).

– Продолжите работу самостоятельно в тетрадях.

Урок 2

В начале урока учитель раздает всем ученикам листочки с одинаковым рисунком:


– Давайте попытаемся ответить на вопрос: «Сколько кружков на рисунке?» – спрашивает учитель и наблюдает за тем, как ученики будут действовать.

Часть детей быстро справляются с поставленной задачей и сообщают учителю «на ушко» верный, а другие – неверный ответ. Некоторые затрудняются.

– Я вижу, что у многих возникли проблемы, – говорит учитель.

– Давайте обсудим, кто как действовал.

– Педагог открывает на доске тот же рисунок и вызывает к доске ученика, который затруднялся ответить на вопрос, (ученик считает по вертикали).

– Кто действовал по-другому? (Несколько учеников выходят к доске, считают круги, сбиваются, ошибаются).

Однако все действуют хорошо известным способом, устанавливая соответствие между каждым кружком и словом числительным (то есть считают).

Находится ученик, который произносит: – Я считал десятками.

Он предлагает посчитать кружки так: 1 дес., 2 дес., 3 дес., 4 дес. На рисунке 4 десятка кружков.

Если никто из детей не предложит нового способа действия, помогает учитель.

– Давайте посчитаем круги в одном ряду. (Их 10 или 1 десяток.)

– А я отвечу на вопрос так: на рисунке 4 десятка кругов.

–— Кто догадался, как получился этот результат? (В одном ряду – 1 дес., в двух – 2 дес., в трех рядах – 3 дес., в четырех – 4 десятка).

– Может быть, теперь вы сможете быстрее ответить на вопрос: «Сколько предметов на рисунке?»

Учитель вывешивает на доску плакаты, на которых 5 десятков предметов, 6 десятков, 3 десятка и 2 единицы, 4 десятка и 5 единиц. В последних двух случаях дети называют число предметов так: «3 десятка и еще 2»; «4 десятка и еще 5».

Учитель корректирует: 3 дес. 2 ед., 4 дес. 5 ед.

– Все вы умеете писать число 3. Но как записать 3 десятка? Умеете писать число 4, но как записать 4 десятка? Кто догадается, как это делать, зная, как пишется число 1 и число 10 (один десяток)?

Учитель записывает на доске числа.

– А как записать числа 3 дес. 2 ед; 4 дес. 5 ед.? (Не все дети могут справиться с этим самостоятельно).

– Этому мы будем учиться. Нашими помощниками будут модель Десятка (треугольник) и модель единицы (кружок).



Далее учитель помещает на доске модели десятков и единиц, а ученики называют количество кружков.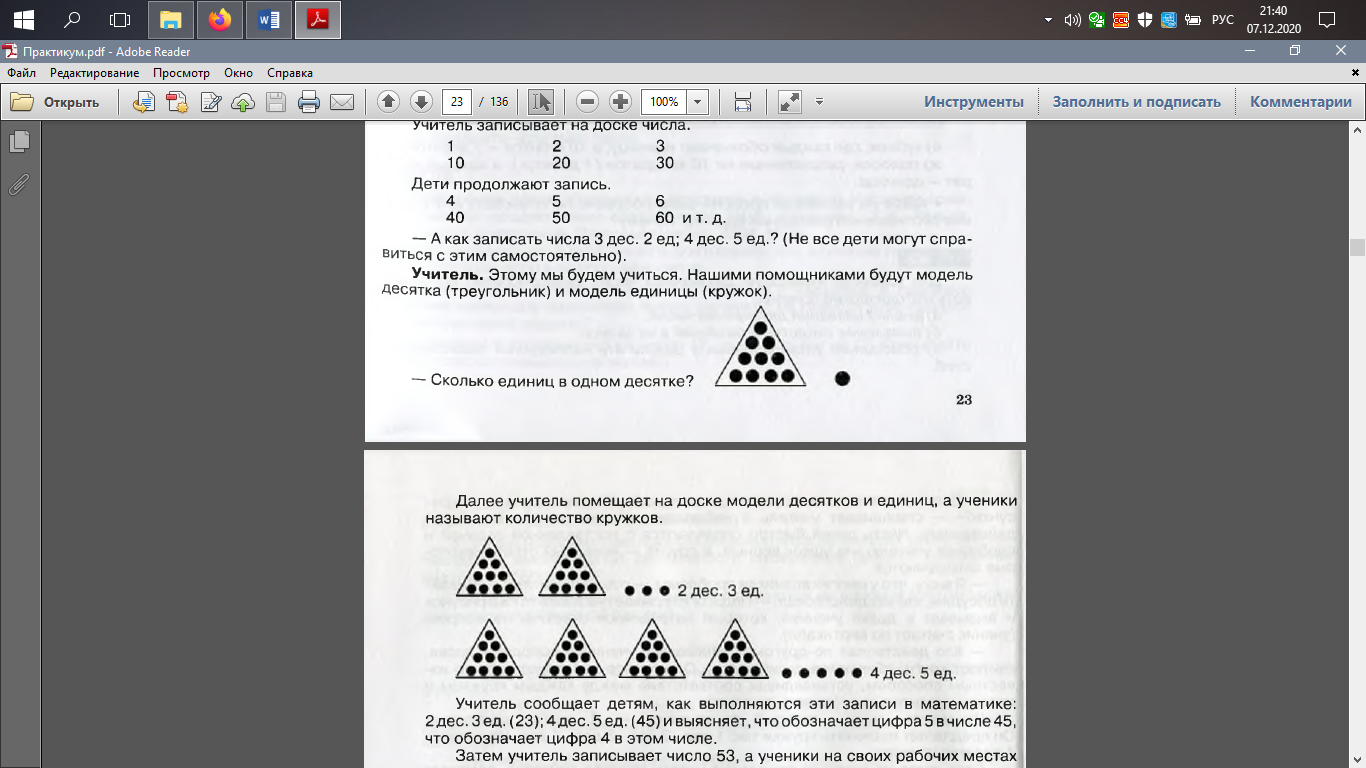



Учитель сообщает детям, как выполняются эти записи в математике: 2 дес. 3 ед. (23); 4 дес. 5 ед. (45) и выясняет, что обозначает цифра 5 в числе 45, что обозначает цифра 4 в этом числе.

Затем учитель записывает число 53, а ученики на своих рабочих местах или на доске выкладывают модели десятков и единиц.

2. Для усвоения нумерации двузначных чисел в школьной практике используют различные наглядные пособия:

а) 10 палочек, связанные в пучок, и отдельные палочки;

б) абак с выдвижными пластинками, под которыми находятся круги разного цвета: одни обозначают десятки, другие – единицы;

в) счеты;

г) модель десятка . , где каждый кружок обозначает единицу;

д) таблица разрядов;



е) кубики, где каждый обозначает единицу, а 10 кубиков – 1 десяток;

ж) полоски, разделенные на 10 квадратов (1 десяток), а каждый квадрат – единица.

Какое из названных пособий целесообразно использовать для усвоения соотношения разрядных единиц? Почему?

3. Для усвоения нумерации двузначных чисел целесообразно использовать методические приемы:

а) анализ названий двузначных чисел;

б) выявление сходства и различий в их записи;

в) обобщение установленных в результате наблюдений закономерностей.

Подберите или составьте сами учебные задания, в которых используются названные приемы.

4. Составьте сами или найдите в учебниках математики для начальных классов задания на классификацию, которые целесообразно предложить учащимся при изучении нумерации двузначных чисел.

5. Вставьте вместо пропусков термины «цифра» или «число», чтобы формулировка заданий была корректной.


1) Сколько__________ используется для записи___________33355?


2) Есть ли в записи__________ одинаковые___________?


3) Что обозначают одинаковые__________ в записи___________?

4) В записи__________ использовались___________3 и 5.

6. Оцените правильность (корректность) использования в речи учителя математической терминологии.


1) Что обозначает цифра 4 в записи числа 48?

2) Выберите числа, в которых отсутствует разряд единиц: 43, 52, 30, 42, 50, 70, 61.

3) В числе 54 содержится 4 единицы.

4) Запишите цифру 10.


5) Что обозначает цифра 5 в записи чисел: 25, 52, 5?

6) Запишите числа, в которых отсутствуют разрядные единицы.

7) Запишите числа, в которых отсутствуют единицы первого разряда.

8) Запишите «круглые» числа.

7. Придумайте или подберите из учебников для начальных классов задание: «Назови лишнее число...», которые можно предложить учащимся при изучении нумерации двузначных чисел.

8. Учитель предложил учащимся для самостоятельной работы задание: «Вставьте пропущенные в этом ряду числа: 8 ....... 11 ....... 14 ... 16 ... 18 ... 20».


Как вы организуете проверку результатов самостоятельной работы?

Познакомьтесь с приведенными ниже способами организации деятельности учащихся при проверке данного задания и поясните, на формирование каких общеучебных умений нацелен каждый способ (слушать, воспринимать и понимать задание учителя; применять ранее усвоенные знания; контролировать себя, выполняя сравнение с образцом или анализируя действия других; общаться друг с другом и с учителем (коммуникативные умения) и т. д.)

1. Беседа с учащимися.


а) Какие числа вы поставили между числами 8 и 11? 11 и 14? 16 и 18? 18 и 20?

б) Назовите число, которое: а) на 1 больше 8; б) на 1 меньше 11; в) на 1 больше 11; г) на 1 меньше 14 и т. д.


в) Какое число получим, если 9 увеличим на 1; если 13 уменьшим на 1; если 8 увеличим на 2; если 14 уменьшим на 1?

2. Сравнение результатов самостоятельной работы учащихся с правильно выполненным заданием на доске. (Учитель предлагает учащимся сверить полученный ряд чисел с тем, который записан на доске. 8 9 10 11 12 13 14 15 16 17 18 19 20)

3. Взаимопроверка. Учитель предлагает учащимся обменяться тетрадями и проверить работу друг друга.

4. Выполнение учащимися работы на доске. На доске заранее заготовлен ряд чисел: 8 ....... 11 ....... 14 ... 16 ... 18 ...

20. Учитель по очереди вызывает учащихся к доске. Они вставляют в окошки числа, а все остальные контролируют их действия и правильность выполнения работы.

5. Проверка тетрадей учащихся. Учитель собирает тетради и проверяет задания.

9. Учитель предложил учащимся задание:

1) увеличьте на 1 числа: 10, 13, 15, 17, 19;

2) уменьшите на один числа: 19, 18, 16, 14, 11.


Какой из приведенных ниже способов выполнения задания вы используете? Почему?

1. Учащиеся записывают только ответы:

1) 11, 14, 16, 18, 20;

2) 18, 17, 15, 13, 10.

2. Учащиеся записывают в одном ряду данные числа, а под ними ответы.

3. Учащиеся записывают равенства:

1) 10+ 1 = 11; 13+ 1 = 14...

2) 1 9 - 1 = 18; 1 8 - 1 = 17...

4. Учащиеся только называют числа.


Какие дополнительные вопросы можно предложить ученикам после того, как они проверят это задание?

Возможны следующие вопросы:


– Какое самое большое число?


– Какое самое маленькое число?

– Прочитайте числа в порядке убывания.


– Чем похожи все записанные числа?

Продолжите составление вопросов.

10. Как организовать деятельность учащихся, чтобы они самостоятельно «открыли» приемы сложения и вычитания:

а) двузначных и однозначных чисел без перехода в другой разряд;

б) двузначных чисел и круглых десятков без перехода в другой разряд;


в) двузначных чисел без перехода в другой разряд?

Составьте фрагмент урока для пунктов а), б), в).


11. Какие знания, умения и навыки необходимы первоклассникам для вычисления значений выражений?

57 – 7 20 + 8 60 – 1 60 – 40

57 – 50 28 + 1 30 + 20 59 + 1

12. Выберите пары выражений, для вычисления значений которых ученики используют один вычислительный прием.

67 – 4 93 – 60 67 + 20 67 + 4

72 + 5 84 – 50 63 + 6 14 + 8

13. При изучении какого случая вычитания целесообразно предложить учащимся следующие вопросы:


а) На сколько можно уменьшить число 47, чтобы в его записи изменялась цифра в разряде единиц?


б) Будет ли твой ответ таким же, если число 47 заменить числом 67, 27, 37, 87, 77?

в) Можно ли назвать другие двузначные числа, для которых ответ будет таким же? Назови эти числа.

Приведите ответы, которые вы предполагаете услышать от учащихся.


Какие способы проверки этих ответов вы планируете использовать?

Ориентируясь на предложенные вопросы, составьте конспект урока, целью которого является усвоение данного вычислительного приема (можно дополнить урок другими заданиями).

14.При изучении какого случая сложения целесообразно предложить учащимся задание: «Верно ли утверждение, что значение сумм в каждой паре одинаково?»

34 + 5 67 + 2 23 + 5

35 + 4 62 + 7 25 + 3

Приведите ответы, которые вы предполагаете услышать от учащихся.


Какие способы проверки этих ответов возможны?

Подберите другие задания для изучения данного случая сложения и составьте конспект урока, целью которого является усвоение и применение этого вычислительного приема.

Какие ранее усвоенные знания применил ученик для вычисления выражения 30 – 6, если он сначала уменьшил число 30 на 1, а затем полученный результат уменьшил на 5?

15. Приведите рассуждения учащихся первого класса при выполнении задания: «По какому признаку можно разбить данные выражения на две группы?»

34 + 20 52 + 30 42 + 3 64 + 4 25 + 2

66 + 3 72 + 20 96 + 3 87 + 2 57 + 40

16. Какие вычислительные навыки совершенствуют учащиеся при сложении (вычитании) «круглых» десятков; при сложении (вычитании) двузначных и однозначных чисел без перехода в другой разряд; при сложении (вычитании) двузначных чисел и «круглых» десятков?

17. Конкретизируйте на примере изучения таблицы сложения и соответствующих случаев вычитания однозначных чисел с переходом в другой разряд этапы формирования навыков табличного сложения:

1) непроизвольное запоминание;

2) установка на запоминание;

3) самоконтроль;

4) контроль.

18. Сформулируйте общий способ действия (вычислительный прием) при сложении двух однозначных чисел с переходом в другой разряд.

Какие предметные, графические и символические модели целесообразно использовать, организуя усвоение учащимися приема сложения однозначных чисел с переходом в другой разряд?

19. Выберите случаи сложения, которые учащиеся начальных классов должны усвоить на уровне навыка: 3 + 4; 9 + 7; 29 + 7; 8 + 4; 5 + 2; 16 + 9; 54+ 8; 6 + 5; 5+ 7.

20. Какими вычислительными приемами могут воспользоваться учащиеся начальных классов при вычислении значений выражений: 14 –- 9, 13 – 8, 15 – 7?


Какие ранее усвоенные знания, умения и навыки применяют учащиеся, используя каждый вычислительный прием?


Какими графическими и предметными моделями можно воспользоваться для обоснования используемых вычислительных приемов?

21. С какой целью учитель предложил ученикам задание: «Запиши данное выражение в виде разности двух чисел, где уменьшаемое – двузначное число, а вычитаемое – однозначное число: а) 11 – 1 – 1; б) 12 – 2 – 3; в ) 13 – 3 – 1»?


Верно ли, что задание можно выполнить двумя способами?

Приведите рассуждения учащихся при выполнении задания одним и другим способом.

22. Как организовать деятельность учащихся, чтобы они самостоятельно «открыли» прием сложения двузначных и однозначных чисел с переходом в другой разряд? Приведите конкретные задания.

23. Составьте выражение, для вычисления значения которого ученики будут пользоваться:

1) приемом вычитания однозначного числа из круглого и приемом вычитания однозначного числа из двузначного с переходом в другой разряд;

2) приемом вычитания однозначного числа из двузначного без перехода в другой разряд и приемом вычитания однозначного числа из двузначного с переходом в другой разряд.

24. Приведите рассуждения учащихся при выполнении заданий.


1) Чем похожи выражения в каждой паре? Чем отличаются?

1) 37 + 4+ 10 2) 28 + 6 + 20 3) 49 + 5 + 30

37+ 10 + 4 28 + 20 + 6 49 + 30 + 5

2) Вычисли значение каждого выражения и запиши верные равенства.

3) Выбери равенства, которые помогут тебе вычислить значения выражений:

49 + 35 28 + 26 37 + 14


С какой целью целесообразно использовать приведенное задание в процессе обучения?

25. Составьте задание с инструкцией: «Разгадай правило, по которому записан ряд чисел...» для проверки умения складывать двузначные и однозначные числа с переходом в другой разряд.

26. С какой целью ученикам предлагается задание: «Какие однозначные числа можно прибавить к числу 67, чтобы в его записи изменились цифры в разряде единиц и десятков»?

27. В какой последовательности целесообразно рассмотреть различные случаи устного сложения и вычитания, формируя у учащихся вычислительные умения?

1) а) 35 + 17; 6) 45 + 20; в) 45 + 2; г) 6 + 9; д) 6 + 3; е) 8 – 2;

2) а) 35 – 7; 6) 15 – 7 ; в) 63 – 28; г) 54 – 30; д) 68 – 5; е) 9 – 4.

28. В чем различие понятий: «вычислительный навык» и «вычислительное умение»? Конкретизируйте свой ответ
Литература:

Байрамукова, П.У. Методика обучения математике в начальных классах: курс лекций / П.У. Байрамукова, А.У. Уртенова. – Ростов н/Д : Феникс, 2009. – С. 5–9.

Белошистая, А.В. Методика обучения математике в начальной школе: курс лекций: учеб. пособие для студентов вузов, обучающихся по спец. «Педагогика и методика начального образования»/ А.В. Белошистая. – М.: Владос, 2007. – С. 12–24.

Дик, Н. Ф. Лучшие инновационные формы внеурочной деятельности в начальной школе / Н.Ф. Дик. – Ростов н/Д.: Феникс, 2009. – С. 42-48.

Истомина, Н.Б. Методика обучения математике в начальных классах: учеб. пособие / Н.Б. Истомина. – М.: Академия, 2002. – 288 с.

Методика и технология обучения математике. Курс лекций: пособие для вузов / под науч. ред. Н. Л. Стефановой, Н. С. Подходовой. – М.: Дрофа, 2005. – 416 с.

Федеральный государственный образовательный стандарт начального общего образования. – М.: Просвещение, 2011. – 33 с.

Эколого-экономические игры и задания: метод. пособие для учителей нач. шк. / А. Ф. Аменд, Н. П. Рябинина, Е. В. Фролова, М. В. Алферова. – Челябинск: изд-во ЧГПУ, 1996. – 58 с.