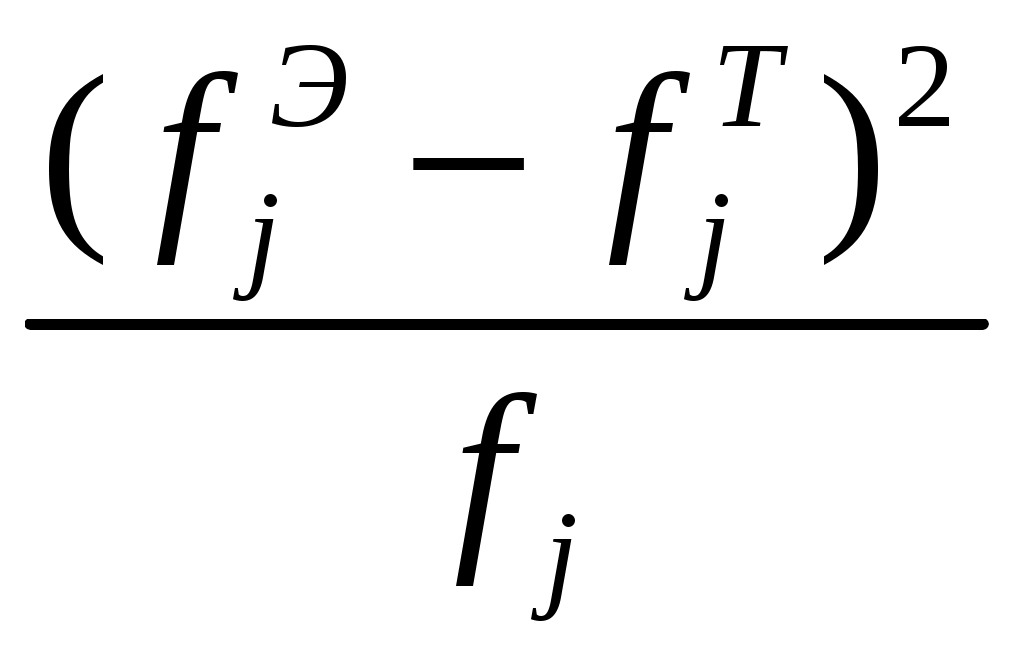Миниобранауки россии

• Название: Миниобранауки россии
• Дата: 05.06.2022
• Размер: 1.37 Mb.
• Имя файла: MetodichkaTV_i_MS_2019.doc
• Тип: Курсовая; #571534
• страница: 4 из 9

Проверка соответствия закона распределения наблюдаемым данным

В данной работе проверяется соответствие опытных данных нормальному закону. В качестве исходных данных используются результаты 2-ого задания.

Проверяется гипотеза

H₀: p(x) = N(0; 1)

Альтернативная гипотеза :

H₁: p(x) ≠ N(0; 1)

Последовательность расчетов:

1.Определяеся число значений признака попадающих в j – ый интервал и среднее значение признака для каждого интервала.

2.Вычисляется среднее значение вариационного рядаx.

3.Вычисляется выборочная дисперсия и стандартное отклонение вариационного ряда.

4.Вычисляются значения функции плотности нормального распределения для каждого интервала по формуле p_j = НОРМРАСП(), в качестве x используется среднее значение на интервале, параметр ИНТЕГРАЛЬНАЯ = 0.

5.Расчитываются теоретические частоты нормального распределения по формуле



где h – длина интервала,n – общее число наблюдаемых значений признака.

6.Расчитывается значение критерия c² по формуле



Данные группируются в таблицу

j	Границы интервала		Эмпирическая частота	Середи­на ин­тервала,	pj(xj, ,σ)	Теоретическая частота
1
2
…
			n
				sx			χ2расч.
					α = 0,05	df =	χ2крит.

8.Вычисляется критическое значение c помощью функции ХИ2ОБРс параметрами ВЕРОЯТНОСТЬ= 0,05; СТЕПЕНИ СВОБОДЫ = k– 3, где k число интервалов.

На основе полученных расчетного и критического значений критерия χ² сделайте вывод о соответствии наблюдаемых данных нормальному закону распределения.

Пример

1. Используя данные расчета проведенного в главе 2, определяем число значений признака попадающих в j-ый интервал и среднее значение признака для каждого интервала.

2. Вычисляем среднее значение вариационного ряда .



3. Вычисляем выборочную дисперсию и стандартное отклонение вариационного ряда.



4. Вычисляем значения функции плотности нормального распределения для каждого интервала по формуле p_j = НОРМРАСП( ), в качестве x используется среднее значение на интервале, параметр ИНТЕГРАЛЬНАЯ = 0 (рис.2). Расчёт сведен в табл.1.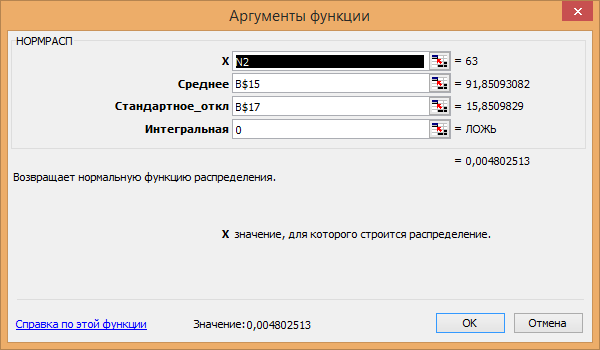



Рис.2. Диалоговое окно «Аргументы функции» для НОРМРАСП.

4. 
   Рассчитываем теоретические частоты нормального распределения по формуле
   

где h – длина интервала, n – общее число наблюдаемых значений признака.

=0,004803x8x31=1,19

Остальные расчёты сведены в табл. 1.

5. 
   Рассчитываем значение критерия c² по формуле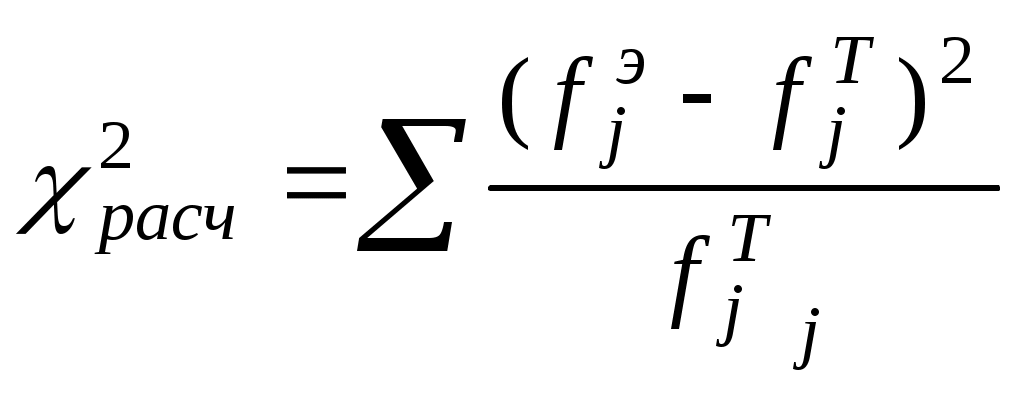
   

7. Вычисляется критическое значение c помощью функции ХИ2ОБР с параметрами ВЕРОЯТНОСТЬ = 0,05; СТЕПЕНИ СВОБОДЫ = k – – 3, где k число интервалов.

Таблица1.

Результаты проверки соответствия закона распределения наблюдаемым данным

j	Границы интервала		Эмпирическая. частота	Середина интервала	Плотность pj (xj, ,σ)	Теоретическая частота
1	59	67	3	63	0,004803	1,191023	2,747551
2	67	75	3	71	0,010595	2,62761	0,052776
3	75	83	1	79	0,018119	4,493419	2,715967
4	83	91	5	87	0,024017	5,956187	0,153503
5	91	99	9	95	0,024676	6,119769	1,355562
6	99	107	4	103	0,019653	4,873906	0,156694
7	107	115	4	111	0,012132	3,008809	0,326528
8	115	123	2	119	0,005805	1,439751	0,218009
							7,72659
							11,0705

8. Вывод о нормальности распределения данных.

Так как , то гипотеза о нормальности распределения СВ принимается.