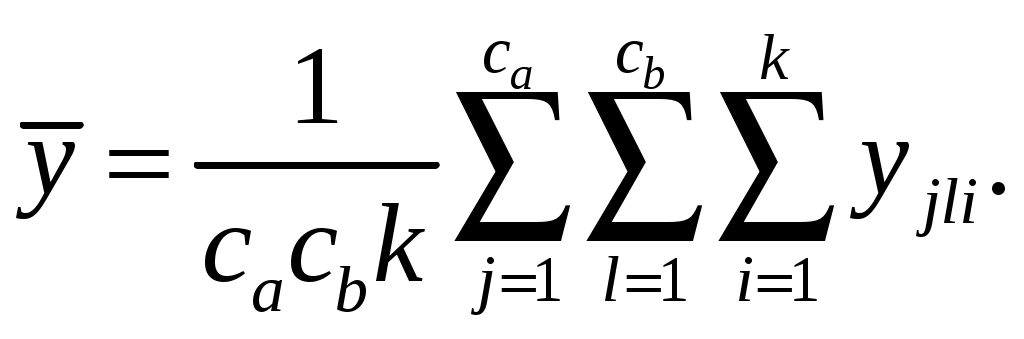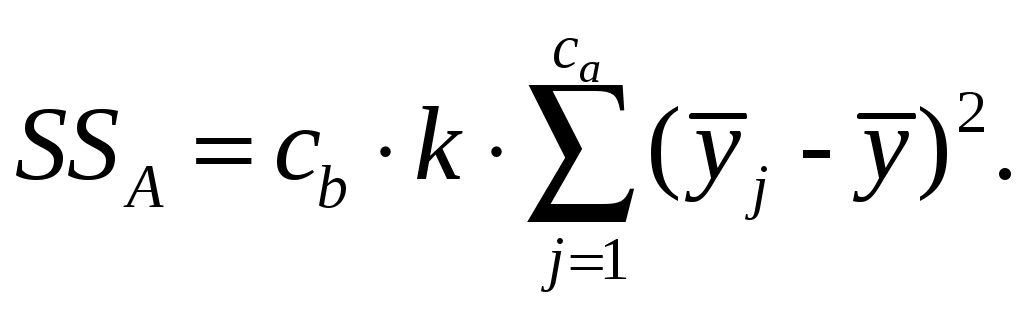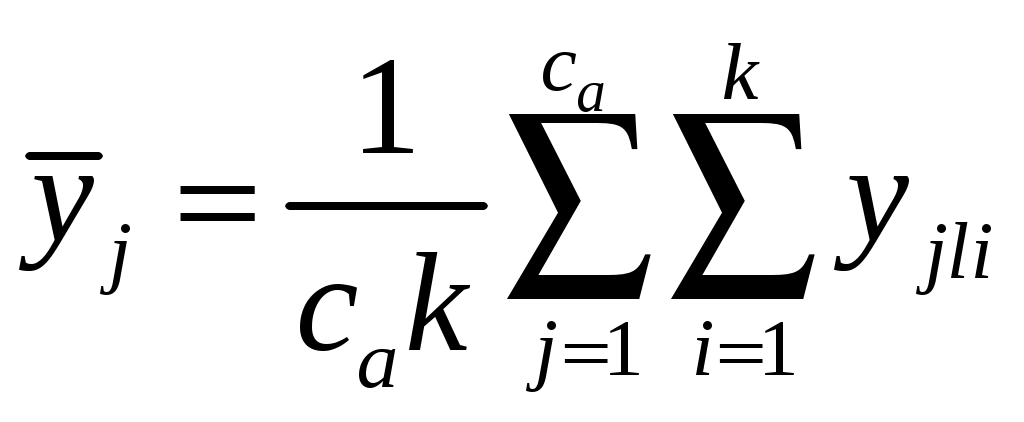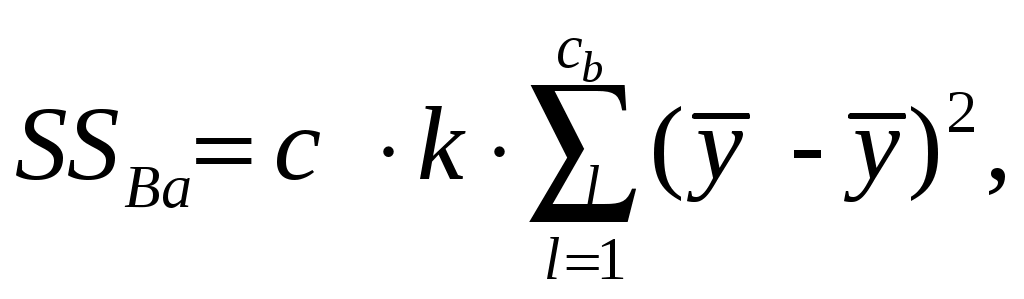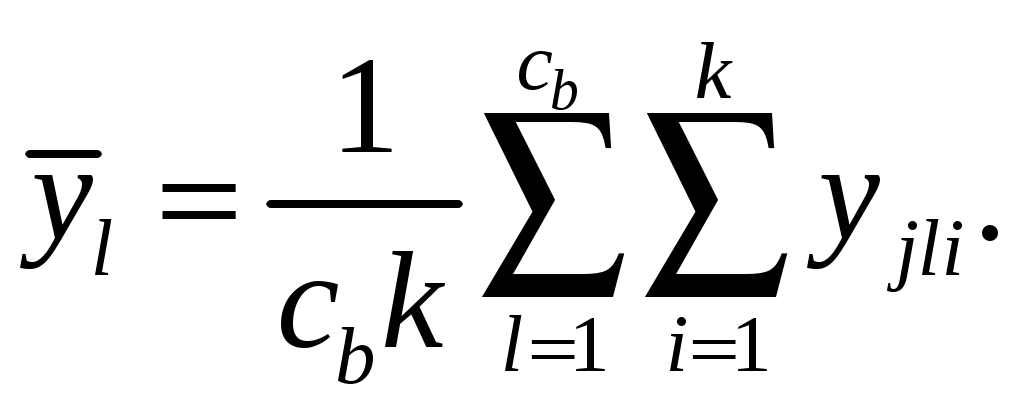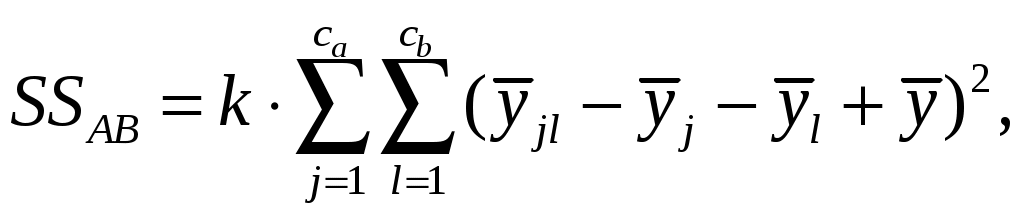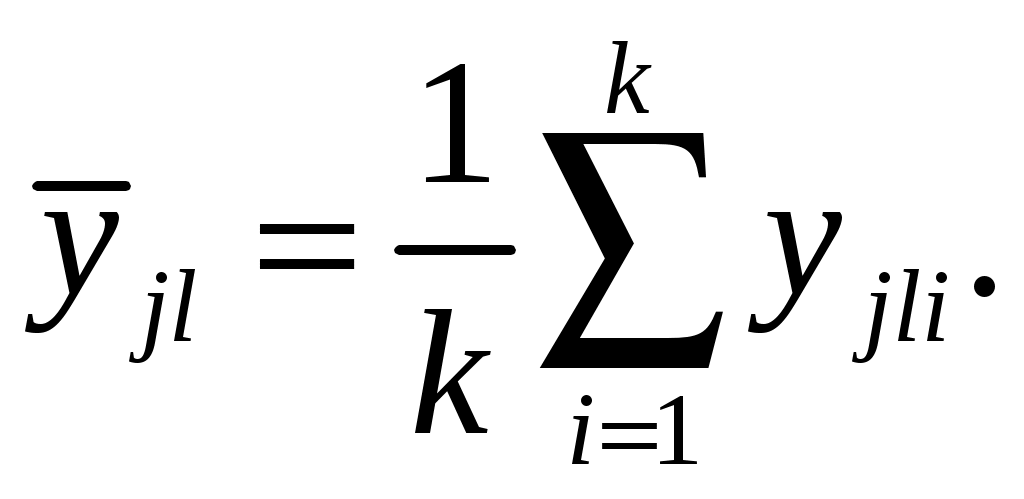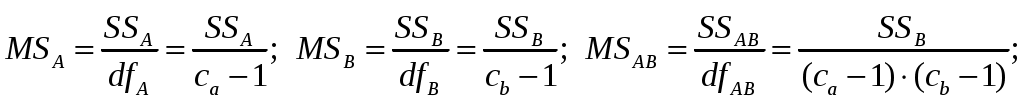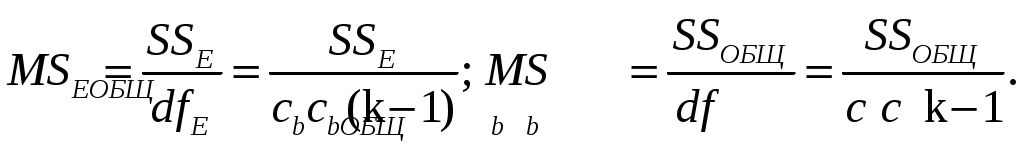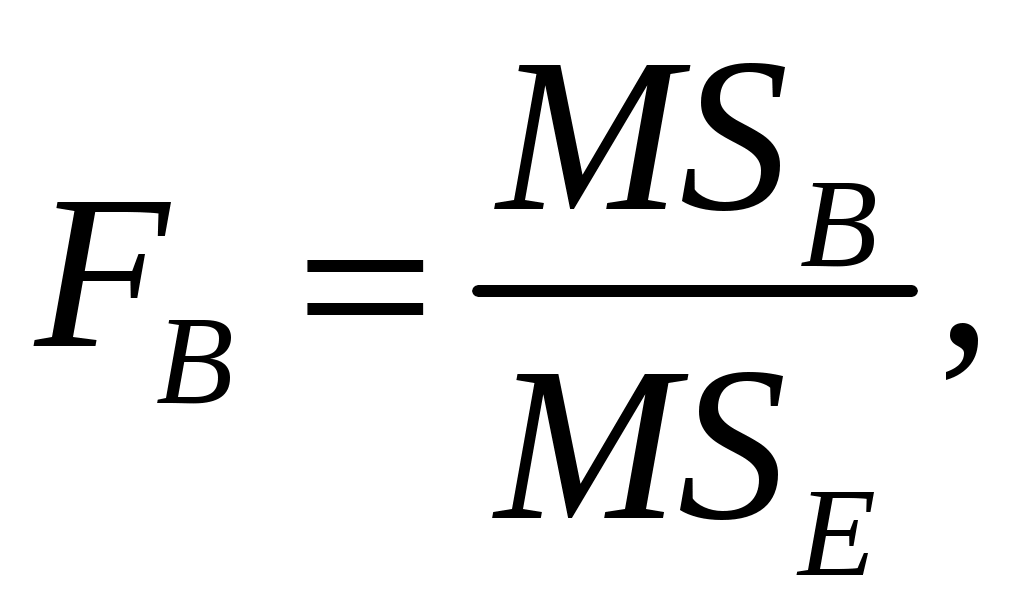Аналогично задаче однофакторного дисперсионного анализа можно рассмотреть задачу о действии на результативный признак Y двух факторов – A и B. Логика однофакторного и двухфакторного дисперсионного анализа во многом схожа и состоит в следующем.
Пусть 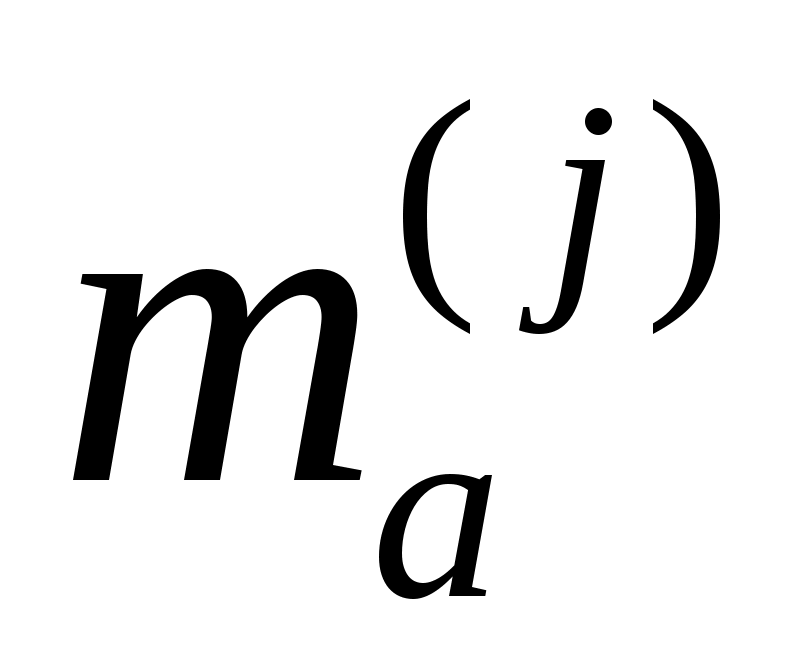 – математическое ожидание результативного признака Y при уровне A(j) (j = 1, 2, … ca); – математическое ожидание результативного признака Y при уровне A(j) (j = 1, 2, … ca); 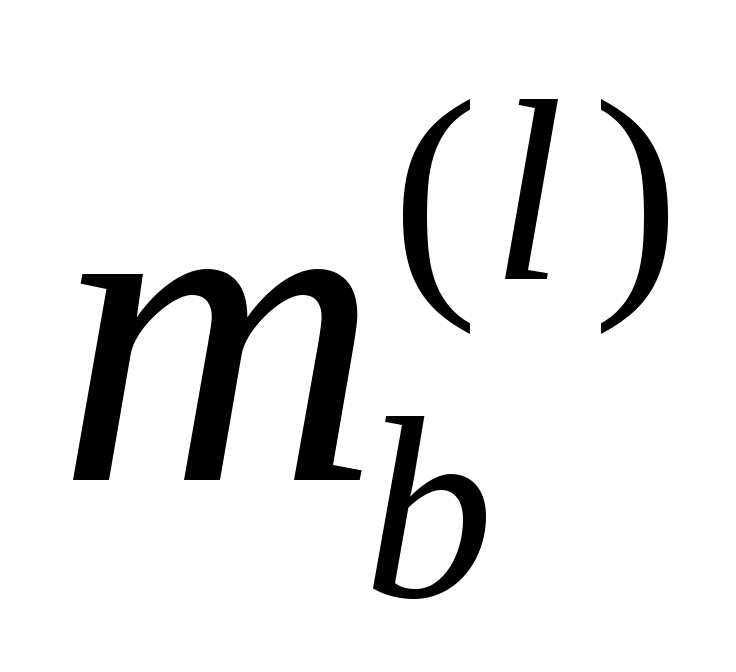 – математическое ожидание результативного признака Y при уровне B(l) (l = 1, 2, … cb). Если при изменении уровня фактора A групповые математические ожидания не изменяются, то считаем, что результативный признак не зависит от фактораА, в противном случае такая зависимость имеется. Аналогично, если при изменении уровня фактора B сохраняется равенство групповых математических ожиданий, то считаем, что Y не зависит от фактора B. Но поскольку числовые значения математических ожиданий неизвестны, возникает задача проверки следующих гипотез: – математическое ожидание результативного признака Y при уровне B(l) (l = 1, 2, … cb). Если при изменении уровня фактора A групповые математические ожидания не изменяются, то считаем, что результативный признак не зависит от фактораА, в противном случае такая зависимость имеется. Аналогично, если при изменении уровня фактора B сохраняется равенство групповых математических ожиданий, то считаем, что Y не зависит от фактора B. Но поскольку числовые значения математических ожиданий неизвестны, возникает задача проверки следующих гипотез:
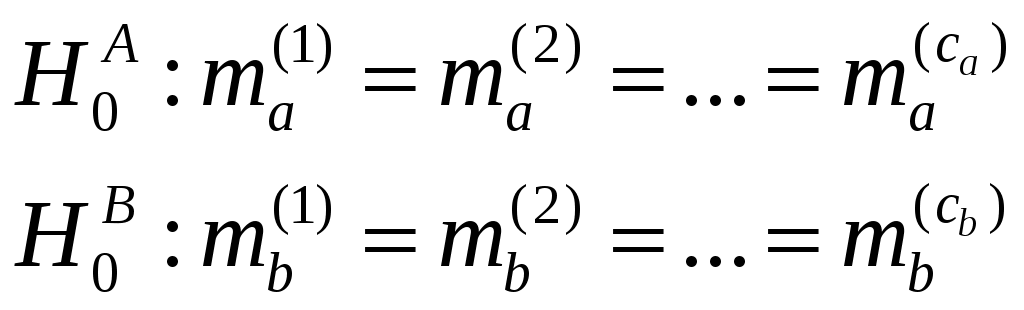
Проверять эти гипотезы, так же как и в задаче однофакторного дисперсионного анализа, можно только при соблюдении следующих требований:
1) при различных сочетаниях уровней факторов A и B наблюдения независимы;
2) при каждом сочетании уровней факторов A и B результативный признак Y имеет нормальный закон распределения с постоянной для различных сочетаний генеральной дисперсией σ2.
Основой проведения двухфакторного дисперсионного анализа служит комбинационная группировка по двум факторам с последующим разложением полной вариации результативного признака SSОБЩ на сумму вариаций фактора A и фактора B, вариации взаимодействия и случайной ошибки по формуле
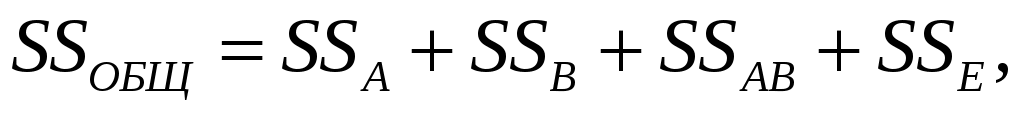
где 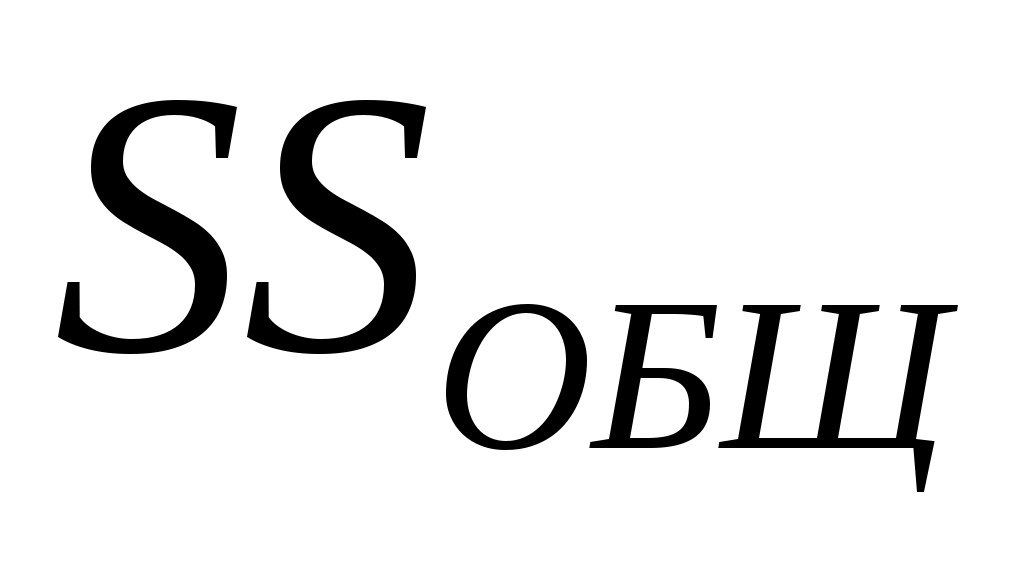 – полная вариация, определяется как полная сумма квадратов отклонения от общего среднего: – полная вариация, определяется как полная сумма квадратов отклонения от общего среднего:
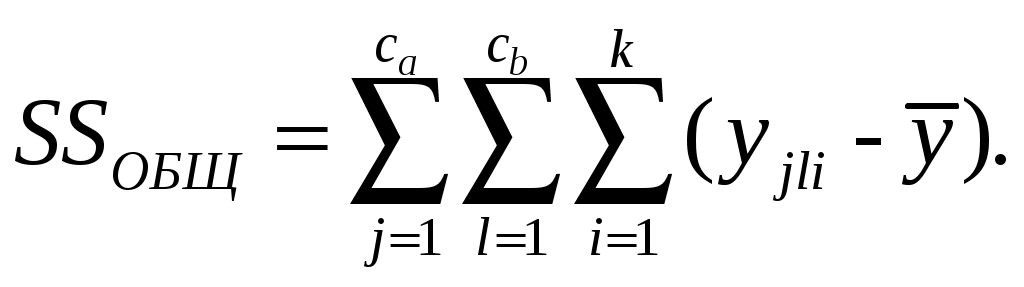 . .
Общее среднее значение равно:
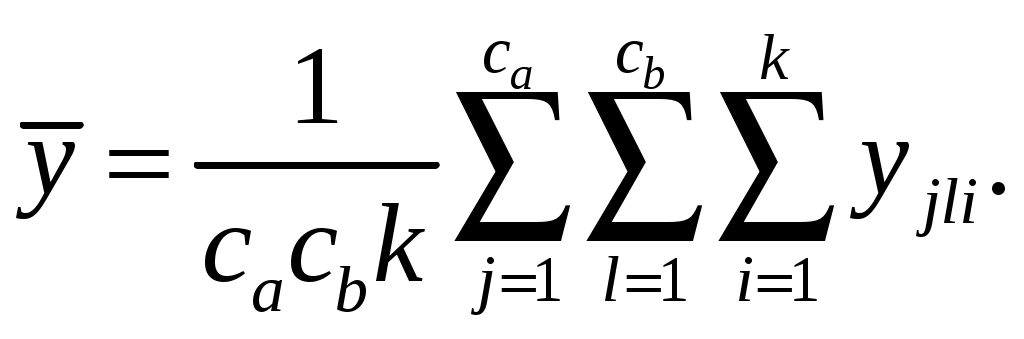
SSА – вариация фактора A, вызванная влиянием на Y фактора A;
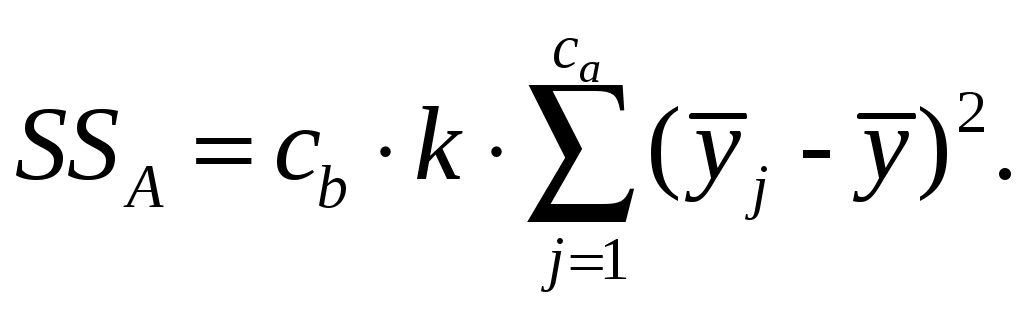
где 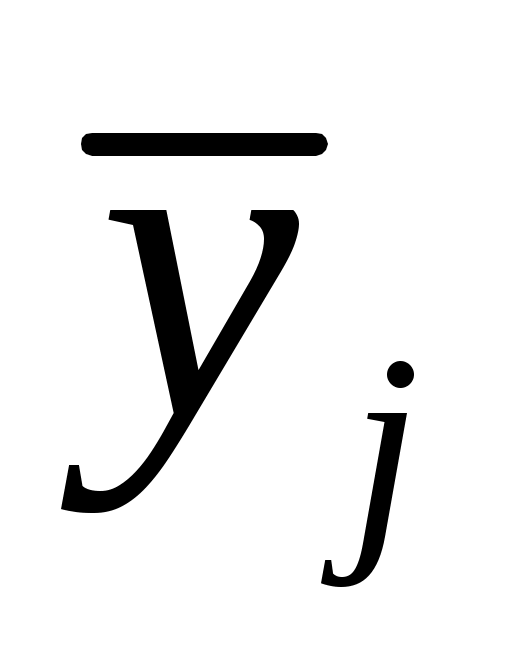 – среднее значение, соответствующее j-ому уровню фактора A – среднее значение, соответствующее j-ому уровню фактора A
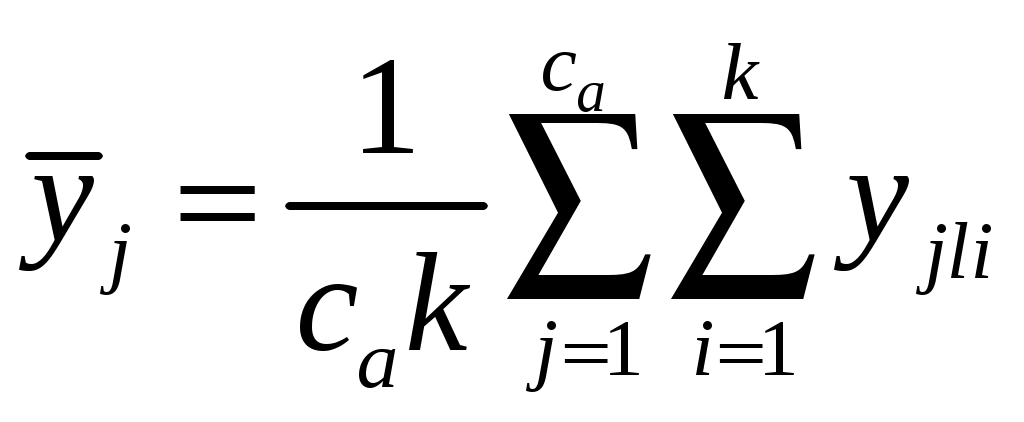
SSВ – вариация фактора В, вызванная влиянием на Y фактора B;
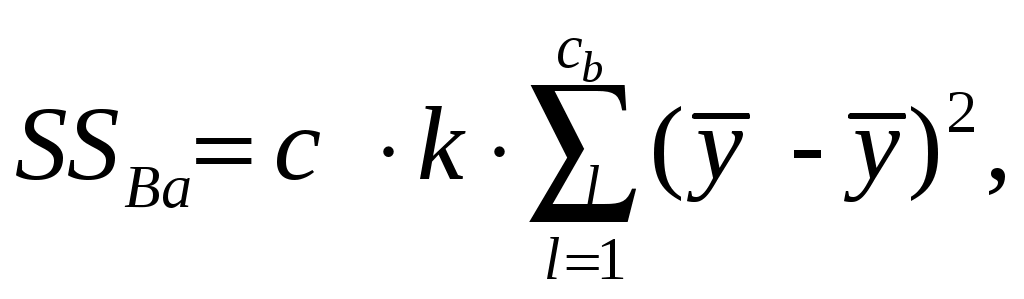
где 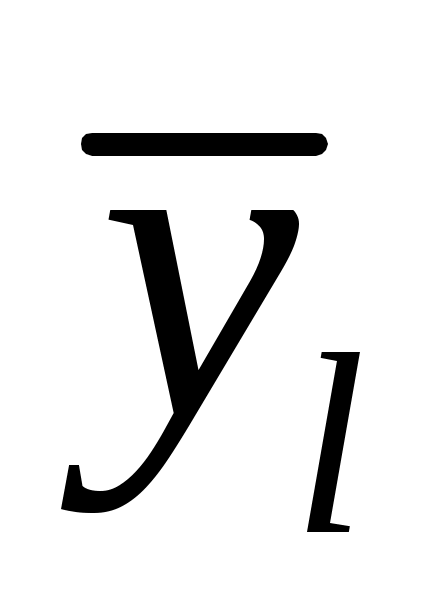 – среднее значение, соответствующее l-ому уровню фактора B – среднее значение, соответствующее l-ому уровню фактора B
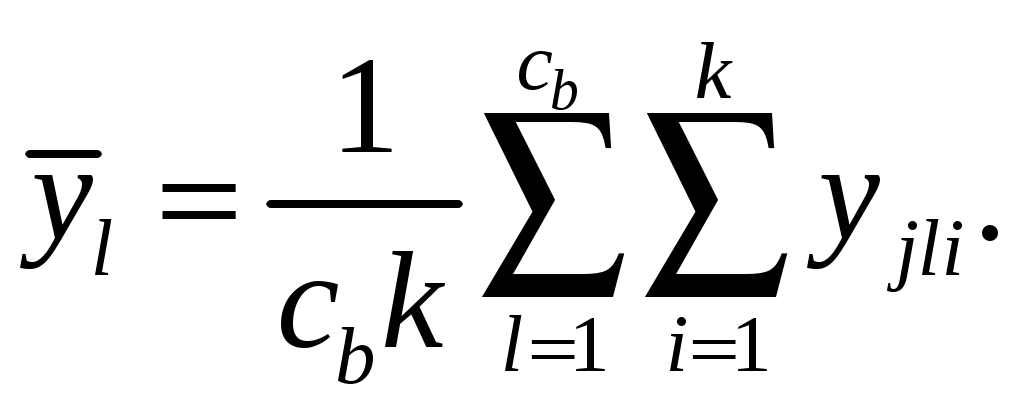
SSВ – вариация взаимодействия. Определяет эффект взаимодействия между факторами A и B.
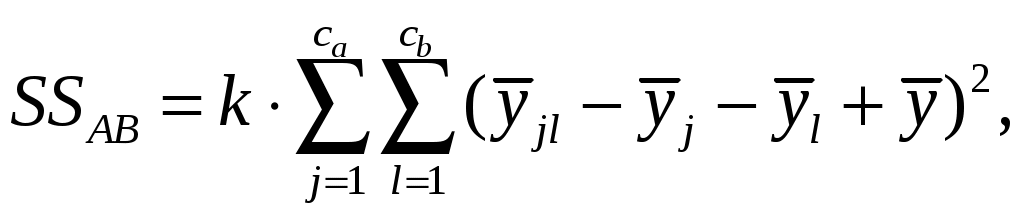
где 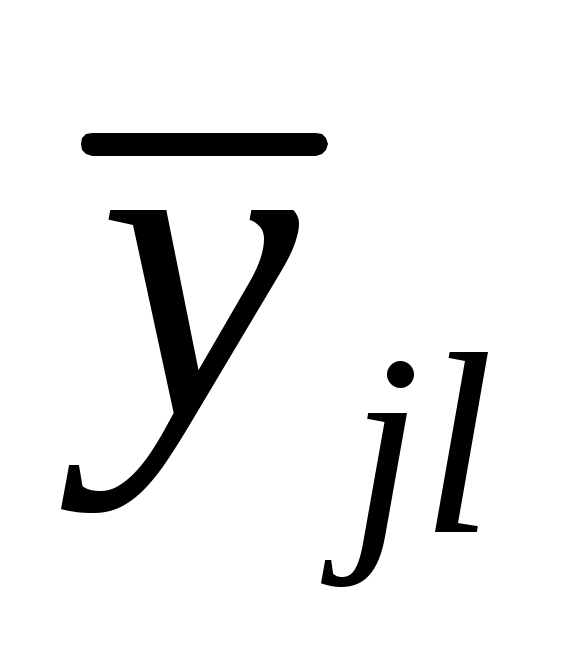 – среднее значение, соответствующее i-ому уровню фактора A и l-ому уровню фактора B – среднее значение, соответствующее i-ому уровню фактора A и l-ому уровню фактора B
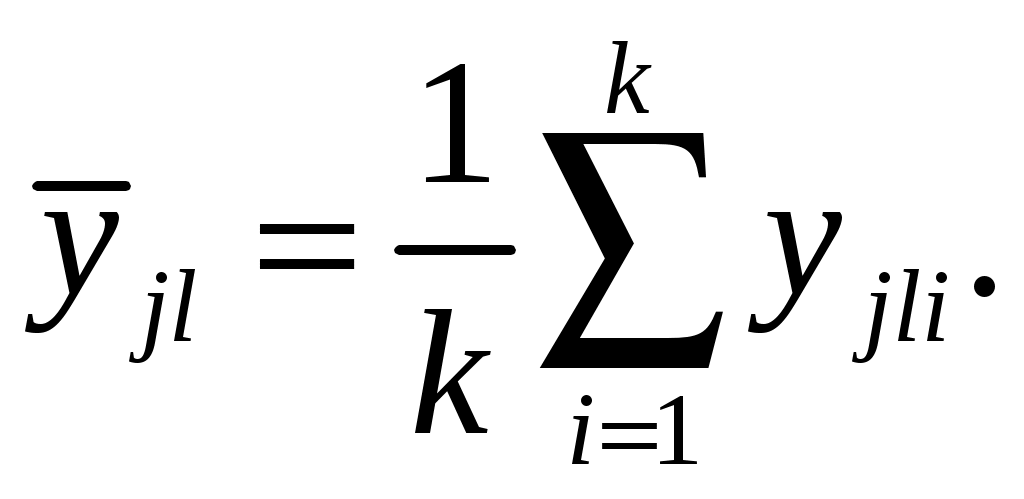
SSВ – случайная ошибка. Показатель вариации, вызванной влиянием на Y остаточных факторов.
Если каждую сумму квадратов отклонений (вариацию) разделить на соответствующее число степеней свободы, то получится четыре типа дисперсии МSА, МSВ, МSАВ, МSЕ.
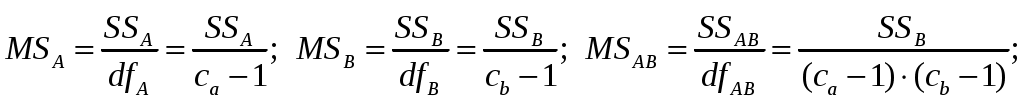
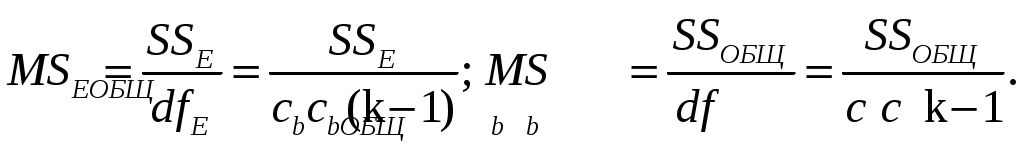
В двухфакторном дисперсионном анализе применяются три разных критерия.
1. Для проверки гипотезы об отсутствии эффекта фактора A 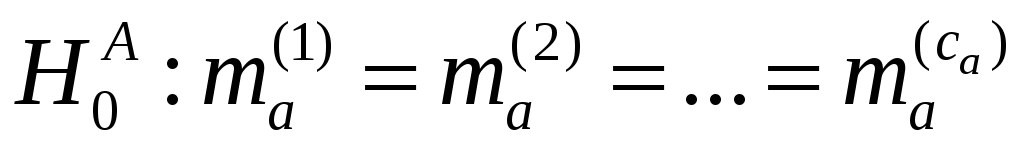 и альтернативной гипотезы H1: не все mj равны используется F-критерий Фишера: и альтернативной гипотезы H1: не все mj равны используется F-критерий Фишера:
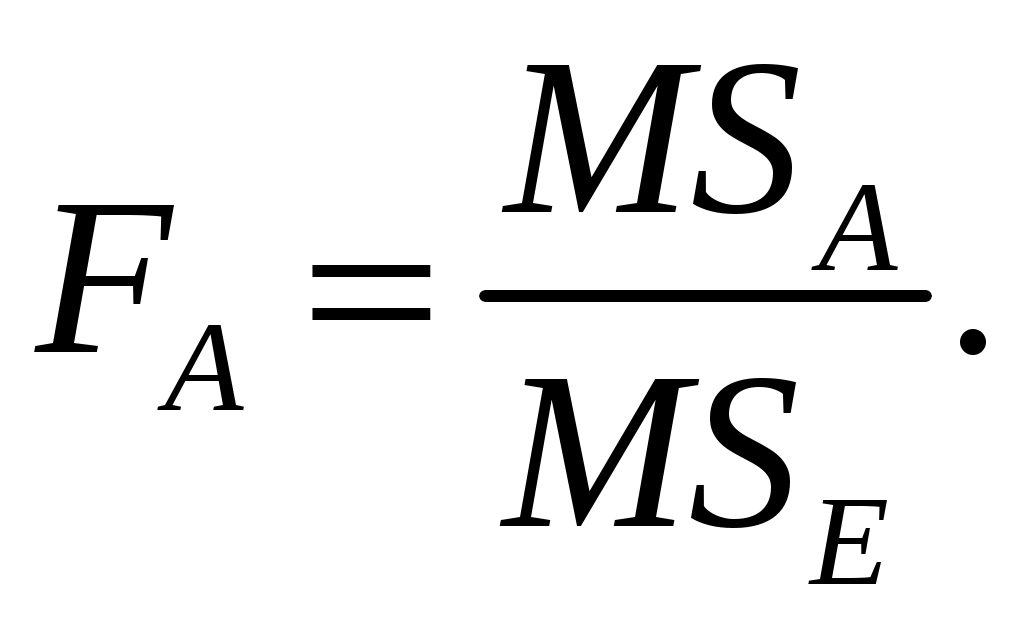
В математической статистике доказывается, что если гипотеза 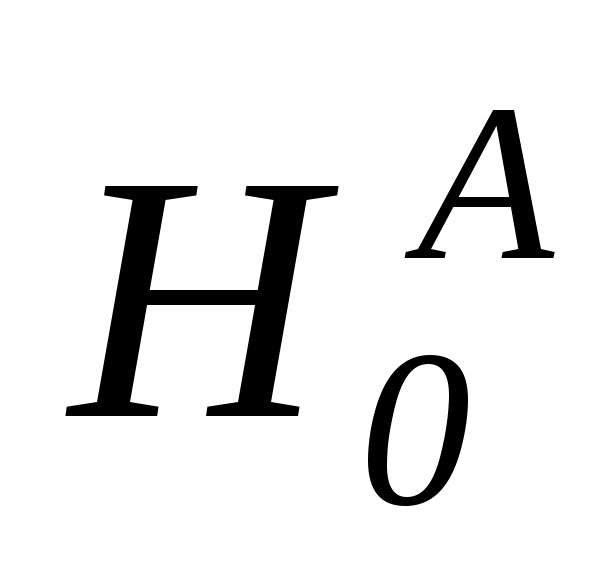 верна, то величина FA имеет F-распределение с числом степеней свободы df1 = (сa – – 1) и df2 = (сА – 1) (сВ – 1). верна, то величина FA имеет F-распределение с числом степеней свободы df1 = (сa – – 1) и df2 = (сА – 1) (сВ – 1).
2. Для проверки гипотезы об отсутствии эффекта фактора B 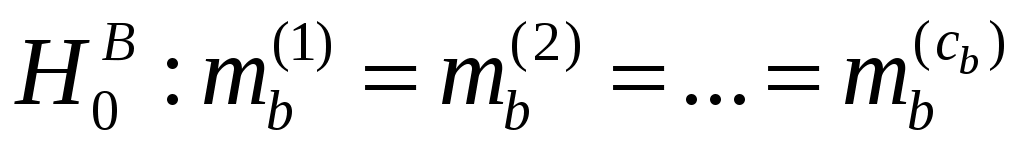 и альтернативной гипотезы H1: не все ml равны используется F-критерий Фишера: и альтернативной гипотезы H1: не все ml равны используется F-критерий Фишера:
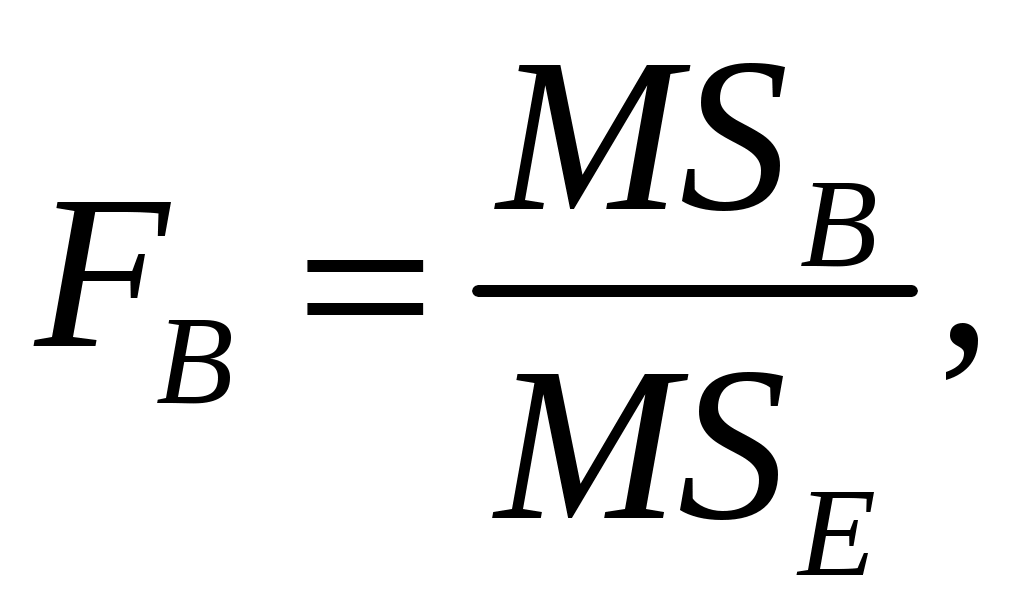
В математической статистике доказывается, что если гипотеза 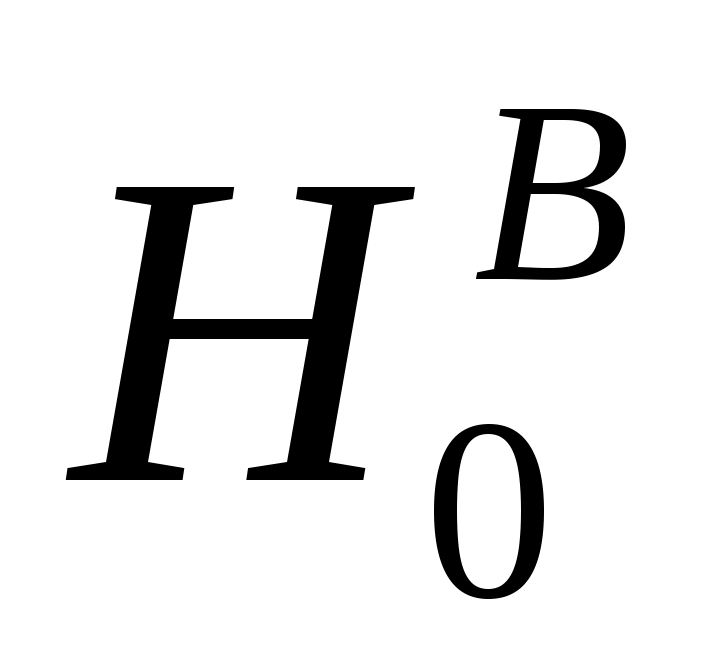 верна, то величина FВ имеет F-распределение с числом степеней свободы df1 = (cb – 1) и df2 = (ca – 1) (cb – 1). верна, то величина FВ имеет F-распределение с числом степеней свободы df1 = (cb – 1) и df2 = (ca – 1) (cb – 1).
3. Для проверки гипотезы об отсутствии эффекта взаимодействия факторов A и B – 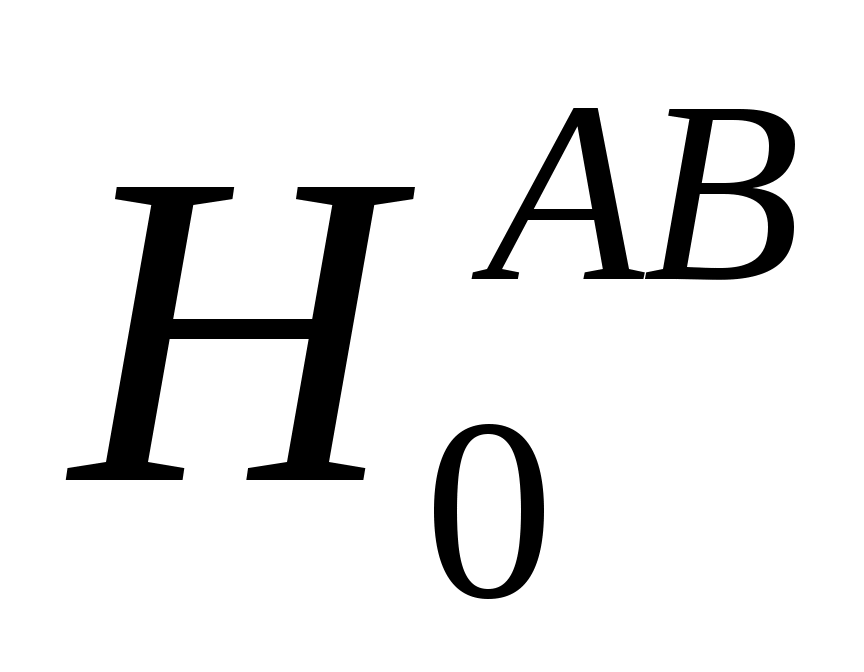 : взаимодействие факторов A и B равно нулю и альтернативной гипотезы – : взаимодействие факторов A и B равно нулю и альтернативной гипотезы – 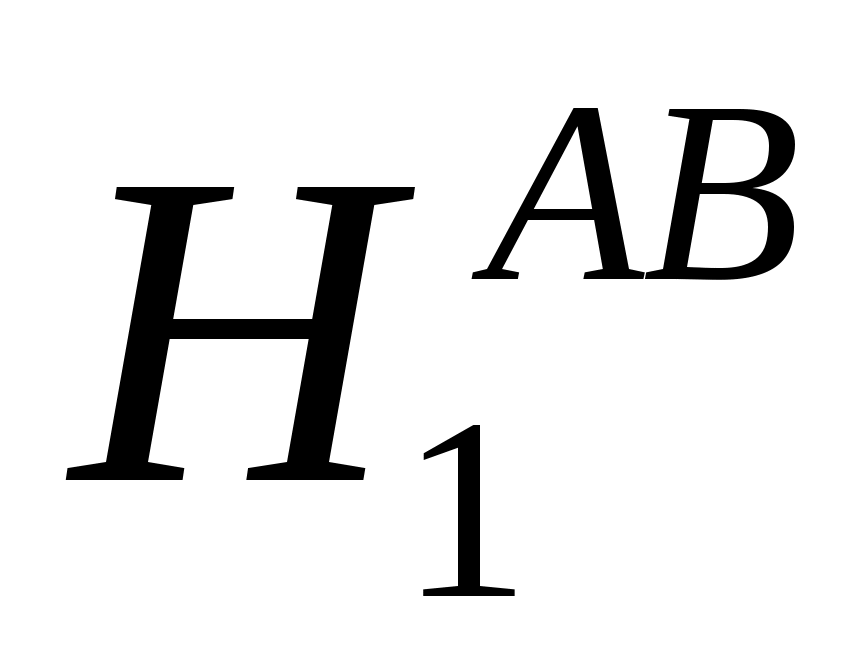 : взаимодействие факторов A и B не равно нулю используется F-критерий Фишера: : взаимодействие факторов A и B не равно нулю используется F-критерий Фишера:
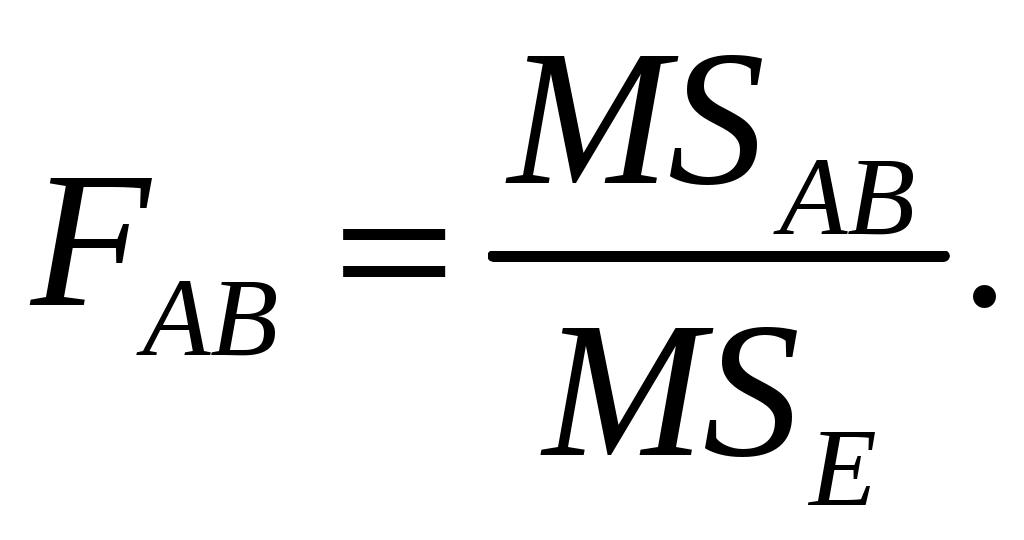
Проверка выдвинутых гипотез осуществляется так же, как и при однофакторном дисперсионном анализе, и состоит в нахождении правосторонних критических интервалов 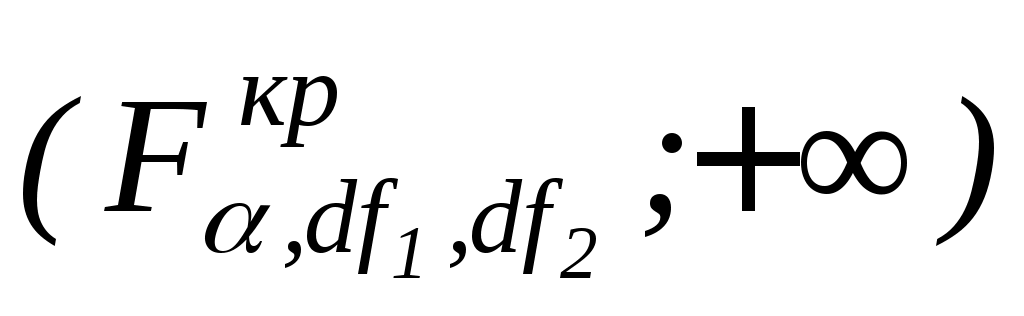 с последующим контролем попадания (или непопадания) в данный интервал расчетных значений FA (или FB) Если расчетное значение попадает в критический интервал, то гипотеза с последующим контролем попадания (или непопадания) в данный интервал расчетных значений FA (или FB) Если расчетное значение попадает в критический интервал, то гипотеза 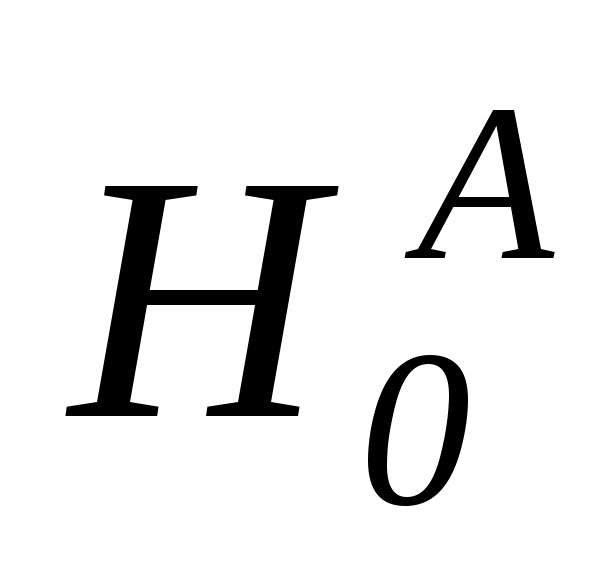 ( (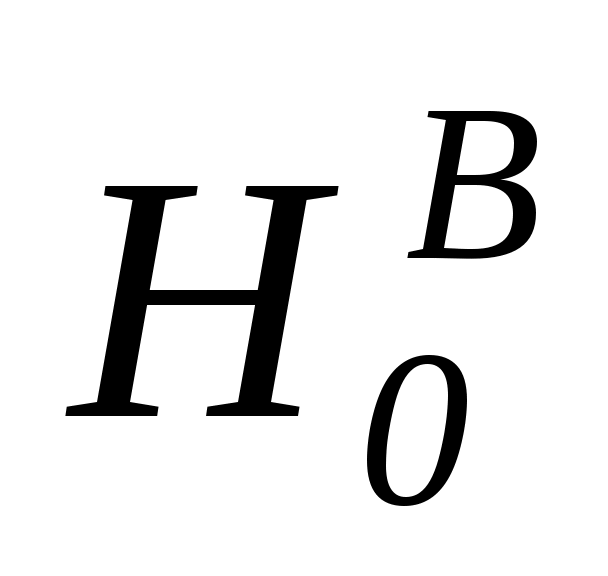 ) отвергается, т.е. считается, что фактор A (B) влияет на результативный признак Y ) отвергается, т.е. считается, что фактор A (B) влияет на результативный признак Y
Двухфакторный дисперсионный анализ может иметь две разновидности: без повторений и с повторениями. В первом случае каждому уровню факторов соответствует только одна выборка данных, во втором — определенным уровням факторов может соответствовать более одной выборки данных.
Пример
1. Сгенерированы исходные данные для анализа, представленные в табл.6.
Таблица 6.
Четыре нормально распределённые выборки по 2 на каждую переменную
-
|
1-ая
переменная
|
2-ая
переменная
|
3-я
переменная
|
4-ая
переменная
|
1-ая
|
96,56642
|
102,6006
|
117,1175
|
75,17628
|
группа
|
141,3495
|
85,01397
|
84,21796
|
108,8279
|
|
108,3845
|
112,0894
|
89,14946
|
77,90009
|
|
83,816
|
91,26086
|
92,55361
|
74,80965
|
|
141,8192
|
117,6365
|
95,43391
|
125,2423
|
|
87,72672
|
126,2366
|
101,8187
|
87,86416
|
|
86,15352
|
103,9551
|
86,88417
|
107,3838
|
|
73,1155
|
84,20715
|
80,73287
|
86,10379
|
|
97,04241
|
84,0885
|
65,27771
|
94,44711
|
|
89,59141
|
129,1113
|
73,73314
|
118,9077
|
2-ая
|
84,05879
|
83,02714
|
111,2919
|
100,1878
|
группа
|
87,90936
|
82,06905
|
74,1734
|
119,4141
|
|
93,14024
|
75,46683
|
126,9855
|
71,48985
|
|
107,2834
|
80,61729
|
85,59402
|
78,89242
|
|
55,35531
|
73,1825
|
98,2151
|
107,6148
|
|
70,82559
|
76,22452
|
66,0066
|
106,3478
|
|
63,48997
|
83,27096
|
96,75027
|
91,89195
|
|
104,5162
|
70,56275
|
92,17939
|
88,00212
|
|
97,39804
|
107,8439
|
101,0735
|
94,61252
|
|
111,1621
|
103,8345
|
83,60792
|
127,2286
|
2. Проведения двухфакторного дисперсионного анализа с повторениями для выяснения на основе выборочных данных табл.6 факта влияния контролируемых факторов A(группа) и B(переменная) на результативный признак Y.
Таблица 7
Результаты анализа
Двухфакторный дисперсионный анализ с повторениями
|
|
|
|
|
|
|
|
|
ИТОГИ
|
1-ая переменная
|
2-ая переменная
|
3-я переменная
|
4-ая переменная
|
Итого
|
|
1ая-гр
|
|
|
|
|
|
|
Счет
|
10
|
10
|
10
|
10
|
40
|
|
Сумма
|
1005,565
|
1036,2
|
886,919
|
956,6627
|
3885,347
|
|
Среднее
|
100,5565
|
103,62
|
88,6919
|
95,66627
|
97,13367
|
|
Дисперсия
|
553,5287
|
298,6593
|
211,0579
|
338,8565
|
356,1788
|
|
|
|
|
|
|
|
|
2ая-гр
|
|
|
|
|
|
|
Счет
|
10
|
10
|
10
|
10
|
40
|
|
Сумма
|
875,139
|
836,0994
|
935,8775
|
985,682
|
3632,798
|
|
Среднее
|
87,5139
|
83,60994
|
93,58775
|
98,5682
|
90,81995
|
|
Дисперсия
|
363,3798
|
156,4353
|
313,268
|
299,2436
|
294,796
|
|
|
|
|
|
|
|
|
Итого
|
|
|
|
|
|
|
Счет
|
20
|
20
|
20
|
20
|
|
|
Сумма
|
1880,704
|
1872,3
|
1822,797
|
1942,345
|
|
|
Среднее
|
94,03521
|
93,61498
|
91,13983
|
97,11723
|
|
|
Дисперсия
|
479,0908
|
320,9404
|
254,6727
|
304,474
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
Источник вариации
|
SS
|
df
|
MS
|
F
|
P-Значение
|
F критическое
|
Выборка
|
797,2629
|
1
|
797,2629
|
2,516584
|
0,117037
|
3,973897
|
Столбцы
|
360,9016
|
3
|
120,3005
|
0,379732
|
0,767892
|
2,731807
|
Взаимодействие
|
2217,254
|
3
|
739,0846
|
2,332942
|
0,0812
|
2,731807
|
Внутри
|
22809,86
|
72
|
316,8037
|
|
|
|
|
|
|
|
|
|
|
Итого
|
26185,28
|
79
|
|
|
|
|
Анализ полученных результатов и проверка гипотез:
1. Гипотеза 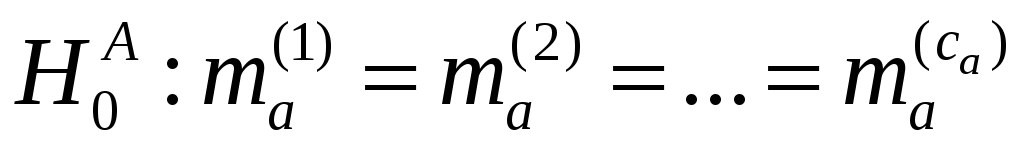 не отклоняется, так как не отклоняется, так как 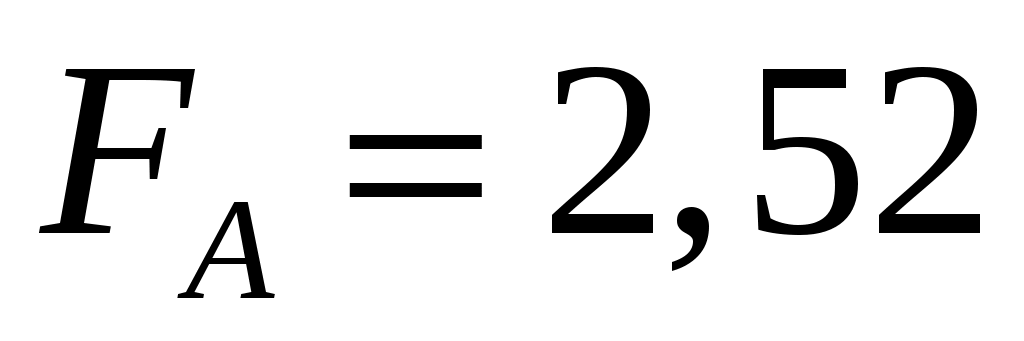 меньше критического значения (соответственно p-значение больше уровня значимости α = 0,05); меньше критического значения (соответственно p-значение больше уровня значимости α = 0,05);
2. Гипотеза 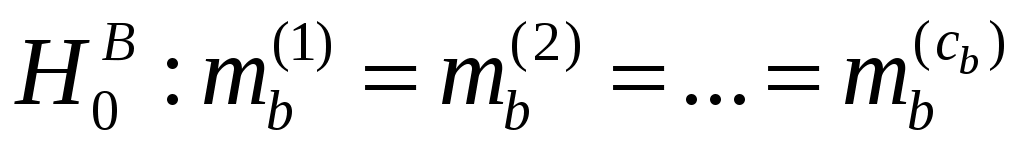 не отклоняется, так как не отклоняется, так как 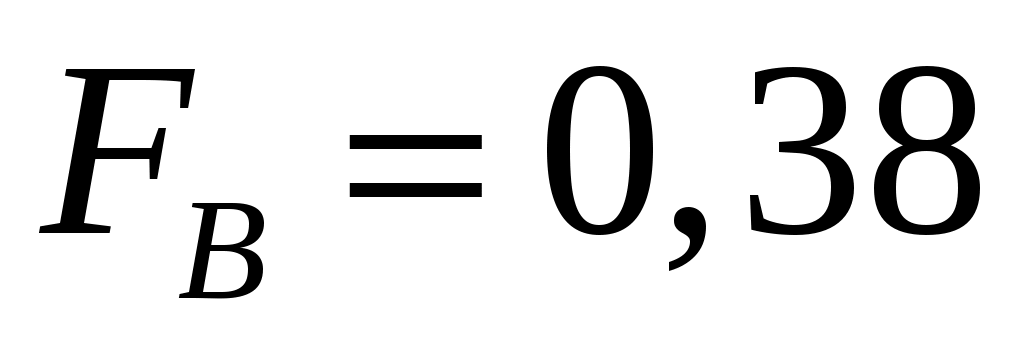 меньше критического значения (соответственно p-значение больше уровня значимости α = 0,05); меньше критического значения (соответственно p-значение больше уровня значимости α = 0,05);
3. Гипотеза 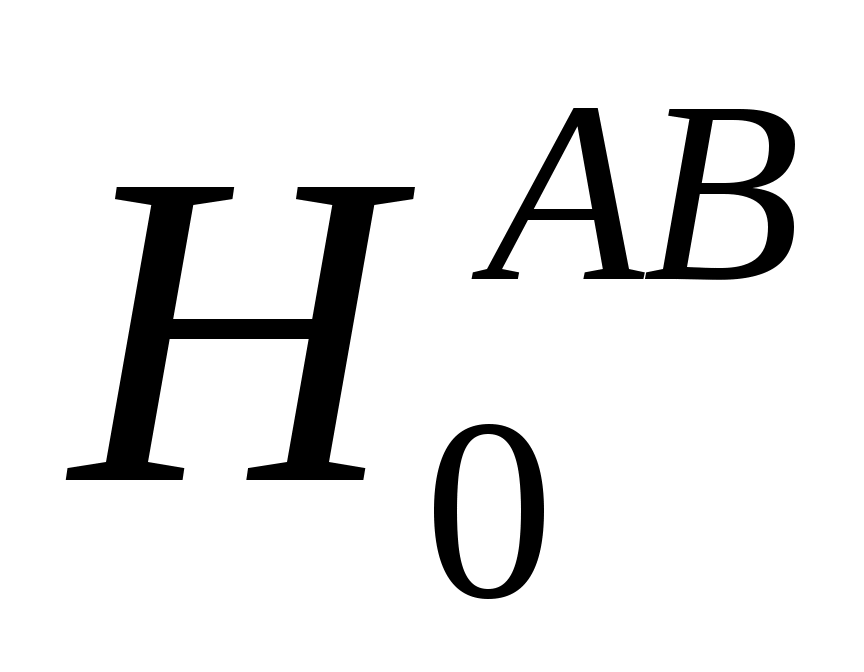 не отклоняется, так как не отклоняется, так как 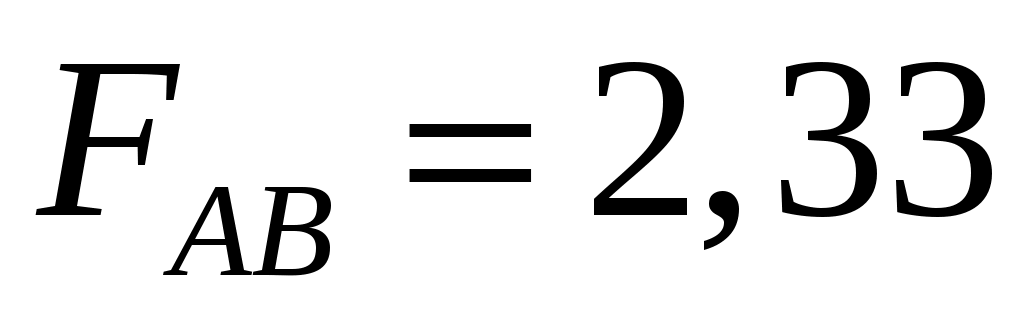 меньше критического значения (соответственно p-значение больше уровня значимости α = 0,05). меньше критического значения (соответственно p-значение больше уровня значимости α = 0,05).
|
 Скачать 1.37 Mb.
Скачать 1.37 Mb.
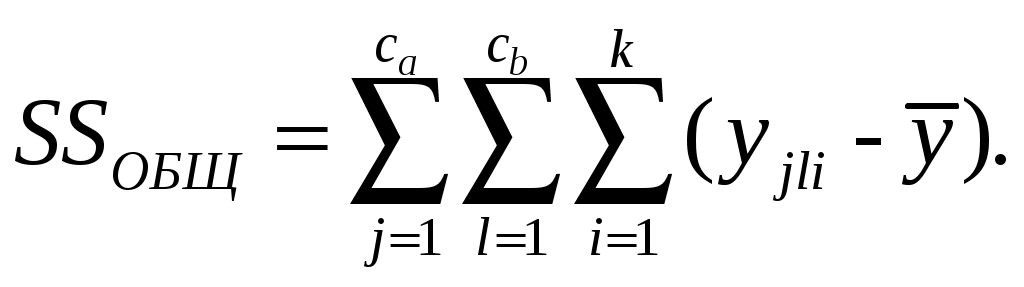 .
.