Миниобранауки россии

• Название: Миниобранауки россии
• Дата: 05.06.2022
• Размер: 1.37 Mb.
• Имя файла: MetodichkaTV_i_MS_2019.doc
• Тип: Курсовая; #571534
• страница: 9 из 9

Контрольное задание

Исходные данные для 20 наблюдений приведены в таблице.

	X0	X1	X2	X3	X4	X5
1	9,7	1,59	,26	2,05	,32	,14
2	8,4	,34	,28	,46	,59	,66
3	9,0	2,53	,31	2,46	,30	,31
4	9,9	4,63	,40	6,44	,43	,59
5	9,6	2,16	,26	2,16	,39	,16
6	8,6	2,16	,30	2,69	,32	,17
7	12,5	,68	,29	,73	,42	,23
8	7,6	,35	,26	,42	,21	,08
9	6,9	,52	,24	,49	,20	,08
10	13,5	3,42	,31	3,02	1,37	,73
11	9,7	1,78	,30	3,19	,73	,17
12	10,7	2,40	,32	3,30	,25	,14
13	12,1	9,36	,40	11,51	,39	,38
14	9,7	1,72	,28	2,26	,82	,17
15	7,0	,59	,29	,60	,13	,35
16	7,2	,28	,26	,30	,09	,15
17	8,2	1,64	,29	1,44	,20	,08
18	8,4	,09	,22	,05	,43	,20
19	13,1	,08	,25	,03	,73	,20
20	8,7	1,36	,26	,17	,99	,42

В соответствии со своим вариантом необходимо:

• 
  построить 3 уравнения линейной регрессии, последовательно увеличивая число факторных переменных от одной до 3;
  
• 
  определить оценки параметров в уравнениях регрессии;
  
• 
  определить качество полученных уравнений регрессии и их статистическую значимость;
  
• 
  оценить статистическую значимость параметров регрессии;
  
• 
  построить графики остатков для полученных регрессий;
  
• 
  выбрать лучшую модель;
  
• 
  для этой модели рассчитать нормированные коэффициенты _j
  

По каждому пункту сделать выводы.
Варианты задания определяются по списку следующим образом.

В качестве независимой переменной используйте X0

№	X1	X2	X3	X4	X5
1	+		+		+
2	+	+			+
3	+	+	+
4	+		+	+
5	+	+	+
6		+	+	+
7		+	+		+
8		+		+	+
9		+		+

В качестве независимой переменной используйте X1

№	X0	X2	X3	X4	X5
10	+		+		+
11	+	+			+
12	+	+	+
13	+		+	+
14	+	+	+
15		+	+	+
16		+	+		+
17		+		+	+
18		+		+

В качестве независимой переменной используйте X2

№	X0	X1	X3	X4	X5
19	+		+		+
20	+	+			+
21	+	+	+
22	+		+	+
24	+	+	+
25		+	+	+
26		+	+		+
27		+		+	+
28		+		+

9. Простая линейная регрессия

Простая линейная регрессия используется для исследования зависимости двух переменных. Уравнение простой линейной регрессии можно записать в виде

y_i = a₀ + a₁x_i + _i(1)

где ₁,…_n- независимые одинаково распределенные случайные величины, определяющие действие различных неучтенных факторов на изменение результирующего показателя Y.

Для определения оценок параметров в уравнении (1) широко используется метод наименьших квадратов (МНК), суть которого заключается в следующем.

Определим величину e_i следующим образом:

e_i = y_i – (a₀ + a₁x_i).

Величина e_i называется отклонением (остатком) наблюдаемого значения результирующей переменной y_i в i – ом наблюдении от расчетного. Отклонение e_i является оценкой случайной компоненты _i. По­строим оценку параметров (a₀, a₁) так, чтобы сумма их квадратов отклонений была минимальной: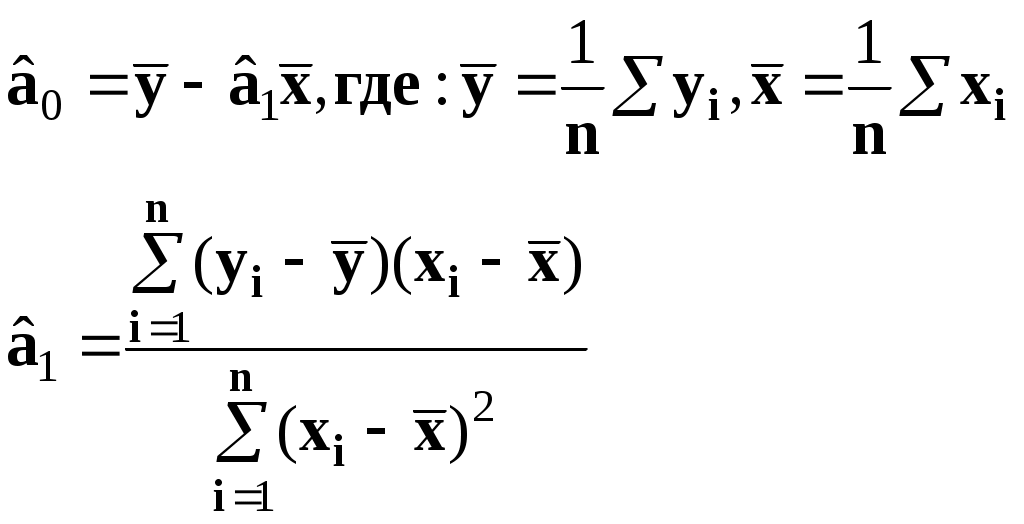

(2)

Сумму минимизируем по (a₀, a₁),приравнивая нулю соответствующие производные.В результате получим систему уравнений линейных относительно a₀ и a₁. Ее решение легко находится:

(3) и (4)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_yx. Для линейной регрессии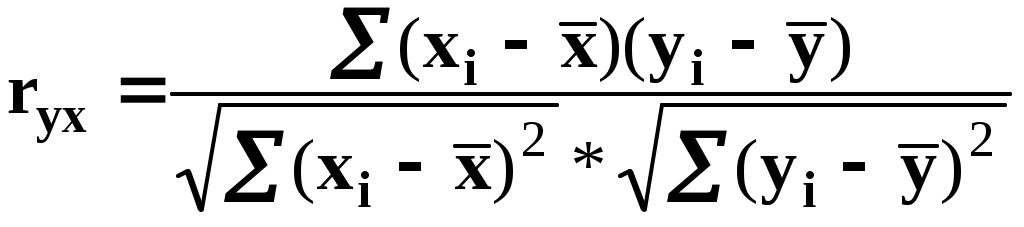
,
Степень тесноты связи результирующей и факторных переменных можно оценить, используя шкалу Чеддока

Значение ryx	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 - 0,99
Степень связи	слабая	умеренная	заметная	высокая	очень высокая

Для определения статистической значимости показателя тесноты связи и существенности связи между результирующей и факторными переменными проводится дисперсионный анализ. Задача состоит в исследовании дисперсии результирующего показателя.

Проверка гипотезы о существенности связи результирующей и факторных переменных в уравнения регрессии (статистической значимости множественного коэффициента корреляции) осуществляется с помощью F-критерия Фишера.

Для проверки вычисляется F-статистика:



где :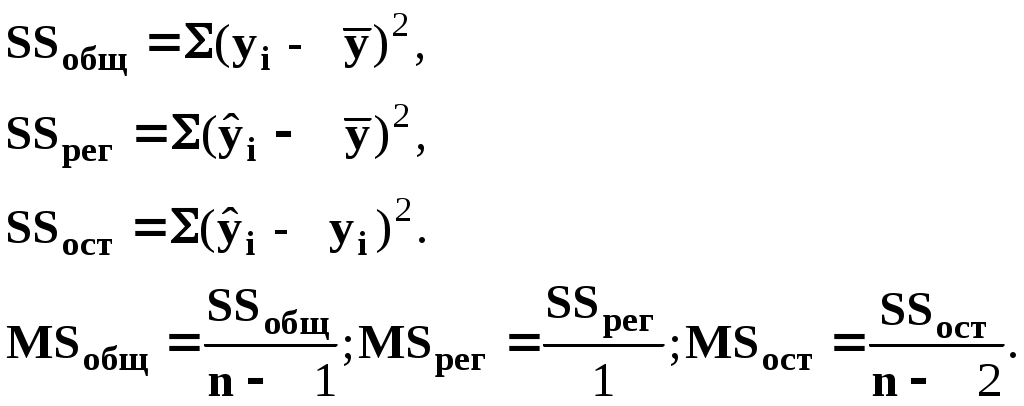



Здесь

- наблюдаемые значения y;

- значения y, вычисленные при соответствующих значениях x;

- среднее значение y.

Из таблиц распределения Фишера определяется критическое значение F_df1,df2,α при заданном уровне значимости α и степенях свободы df₁ = 1, df₂ = n-2, где уровень значимости α – вероятность совершения ошибки первого рода.

Если F_pасч> F_{df1,df2,α ,} то полученное значение множественного коэффициента корреляции можно считать статистически значимым. В противном случае полагаем r_yx = 0, что свидетельствует об отсутствии линейной зависимости между результирующей и факторными переменными в уравнения регрессии

Задание:

Сгенерировать 45 значений случайной величины ε, считая, что случайная компонента ε распределена нормально с нулевым математическим ожиданием и единичной дисперсией. Для вычисления ε использовать генератор случайных чисел.

.


Таблица1

Номер набл.	Значение xi	Номер набл	Значение xi	Номер набл	Значение xi
1	6,5	16	9,3	31	10,4
2	10,3	17	5,7	32	10,2
3	7,7	18	12,9	33	18,0
4	15,8	19	5,1	34	13,8
5	7,4	20	3,8	35	6,0
6	14,3	21	17,1	36	11,9
7	15,4	22	8,2	37	9,4
8	21,1	23	8,1	38	13,7
9	22,1	24	11,7	39	12,0
10	12,0	25	13,0	40	11,6
11	9,5	26	15,3	41	9,1
12	8,1	27	13,5	42	6,6
13	8,4	28	10,5	43	7,6
14	15,3	29	7,3	44	9,9
15	4,3	30	13,8	45	14,7

Рассчитать 45 значений Y используя формулу

Y = 11,5 + (0,14N)x + 2ε (5)

где ε случайная компонента. Значения X возьмите из таблицы 1

Построить таблицу пар (Y,X), подставляя в уравнение (5) значения X из таблицы 1 и сгенерированные значения ε. N = Ваш номер по списку.

Используя данные таблицы (Y,X) рассчитать коэффициенты a₀ и a₁, а также коэффициент корреляции r_yx и записать уравнение регрессии.

Сделать вывод о тесноте связи используя шкалу Чеддока.

Рассчитать F – статистику Фишера и сделать вывод о статистической значимости коэффициента корреляции.

Список литературы

1. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В.Е. Гмурман. – 10-е изд., стер. – М.: Высш. шк., 2004. – 479 с.

2. Ветров, А.Н. Статистические программные системы: учебное
пособие ⁄ А.Н. Ветров, А.Л. Борисов, Ю.Г. Козлова. – Тверь: Тверской
государственный технический университет, 2014. – 152 с.

3. Ветров, А.Н. Методические указания и задания к курсовой работе по дисциплине Теория вероятностей и статистика / А.Н. Ветров. – Тверь: ТвГТУ, 2017. – 25 с.

5. Дисперсионный двухфакторный анализ [Электронный ресурс] // refdb.ru: сайт. – Режим доступа: https://refdb.ru/look/1210036.html

5. Шеффе, Г. Дисперсионный анализ / Г. Шеффе. – М.: Наука, 1980. 512 с.