Океанология. Часть I. Физические явления и процессы в океане - Безруков Ю.Ф.. Океанология. Часть I. Физические явления и процессы в океане - Б. Министерство науки и образования Украины Таврический национальный университет им. В. И. Вернадского

• Название: Министерство науки и образования Украины Таврический национальный университет им. В. И. Вернадского
• Анкор: Океанология. Часть I. Физические явления и процессы в океане - Безруков Ю.Ф..doc
• Дата: 27.05.2017
• Размер: 14.3 Mb.
• Имя файла: Океанология. Часть I. Физические явления и процессы в океане - Б.doc
• Тип: Документы; #8077
• Категория: Геология
• страница: 8 из 21

7. Турбулентное перемешивание в океане

7.1. Типы турбулентного перемешивания

Для Мирового океана характерны два основных типа перемешивания - молекулярное и турбулентное.

Молекулярное перемешивание происходит в результатетеплового взаимодействия между отдель­ными молекулами и носит микроскопический характер броуновского движения. Турбулентноеперемешивание осуществляется за счет перемещения больших объемов воды. Молекулярное перемешивание ассоциируется с ламинарным (слоистым) движением, турбулентное - с турбулентным движением жидкости, которое может быть горизонтальным и вертикальным. Упорядоченный ламинарный характер движения быстро переходит в неупорядоченный, хаотический, турбулентный характер движения. И хотя границы этого перехода весьма расплывчаты, турбулентносгь является процессом доминирующим; перемешивание в океане(как и в атмосфере) является существенно турбулентным, поэтому о перемешивании в океане говорят как о морской турбулентности. Однако,процесс молекулярного перемешивания не уничтожается турбулентностью, а продолжает существовать как бы внутри нее.

Морскую турбулентность, в свою очередь, можно разделить на два основных класса:

1. Динамическую турбулентность (по А.Дефанту), или адвективное (фрикционное) перемешивание (по Н.Н.Зубову). Динамическая турбулентность возникает вследствие наличия в жидкости градиентов скорости и вызванной ею передачи количества движения и других свойств жидкости из одной области в другую.

2. Гравитационную турбулентность (по А.Дефанту), или конвективное перемешивание (по Н.Н.Зубову). Возникает вследствие появления в жидкости отрицательных градиентов плотности и, следовательно, гравитационной

неустойчивости, вызывающих образование вертикальных конвекционных потоков, перемешивающих жидкость до степени однородности.

Динамическая турбулентность может существовать как в однородной, так и в неоднородной, или стратифицированной жидкости; гравитационная турбулен­тность может существовать лишь в неоднородной жидкости - при нарушении устойчивой стратификации. Динамическая турбулентность представляет преобладающее, стационарное явление, гравитационная – временное, нестационарное явление, возникающее вследствие суточного и сезонного изменения плотности воды.

Конвективное перемешивание может быть разделено на два класса - термохалинную конвекцию и целлюлярную (ячеистую) конвекцию.

Термохалинная конвекция возникает из-за понижения температуры или повышения солености, или же из-за совместного действия этих фактoров, вызывающих появление плотностной неустойчивости, и, как следствие, появление верикальных конвективных токов. В зависимости от причин, вызывающих конвекцию, она может быть разделена на три типа: термохалинная конвекция, возникающая в результате осолонения при льдообразовании, понижения температуры и осолонения при испарении.

В зависимости от сочетания этих факторов термохалинная конвекция может быть разделена на пять основных климатических типов - полярный, арктический, субарктический, субтропический и тропический.

Выделяется также тип термохалиниой конвекции, возникающий в результате уплотнения при смешении вод. Этот тип встречается там, где в соприкосновение приходят воды, значитeльно отличающиеся между собой потемпературе и солености.

Целлюлярная конвекция представляет тип упорядоченного перемешивания, причиной которого является та же плотностная неустойчивость. Однако, целлюлярная конвекция происходит в условия, близких к равновесным. Примерами целлюлярной конвекции служат конвекция в ячейках Бенара в приповерхностных слоях моря и конвекция в ячейках Рэлея в придонных слоях океана.

7.2. Вязкость (или сила внутреннего трения)

Вязкость (или сила внутреннего трения) характеризует обмен количеством движения между соседними слоями жидкости. Проявление сил трения происходит вследствие молекулярного перемешивания – проникновения отдельных молекул из одного слоя в другой.

Вязкость обычно рассматривается:

а) какфизическое свойство морской воды, когда исследуются процессы в условиях ламинарного движения при малых скоростях. В этом случае она называется молекулярной вязкостью и характеризуется коэффициентом молекулярной вязкости μ.

При изучении течений, где наблюдается взаимодействие сил трения и сил инерции обычно пользуются коэффициентом кинематической вязкости ν, который равен произведению коэффициента молекулярной вязкости на удельный объем жидкости ν = μ · α.

Вязкость, или сила внутреннего трения τ, определяется по формуле Ньютона:

, она же, отнесенная к единице объема, равна ,

где μ- коэффициент молекулярнои вязкости, - градиент скорости в направлении z.

б) какхарактеристика возможности и интенсивности перемешивания при различных динамических процессах, в основном вихревых, сопровождающихся перераспределением и выравниванием океанологических параметров. В этом случае она называется турбулентной вязкостью τ' = А, где А – турбулентная вязкость, а сама формула выражает турбулентное касательное напряжение τ' (гипотеза Т.Буссинеска). Она отличается от формулы молекулярного трения Ньютона тем, что в ней фигурирует градиент осредненной скоростиU, вместо истинной скорости u.

В системе СГС(сантиметр-грамм-секунда) единицей коэффициента молекулярной вязкости, называемого также коэффициентом внутреннего трения, принят пуаз (г · см^-1 · с^-1). Для кинематической вязкости единицей измерения принят стокс (см² · с^-1).

Вязкость морской воды увеличивается с повышением солености и резко уменьшается с повышением температуры.

При рассмотрении большинства процессов, протекающих в океане, молекулярной вязкостью обычно пренебрегают, так как она в тысячи раз меньше турбулентной вязкости. Передача же количества движения от поверхности в глубинные слои за счет турбулентной вязкости происходит очень быстро крупными объемами воды при вихревом движении.

Однако для таких процессов, как осаждение взвешенных в воде твердых частиц и мельчайших живых организмов (планктона), молекулярная вязкость имеет существенное значение. Так скорость осаждения твердых частиц пропорциональна квадрату их радиуса и обратно пропорциональна коэффициенту молекулярной вязкости. Поэтому, зная коэффициент вязкости, можно определить размеры частиц по скорости их осаждения, что используется при определения размеров частиц морских грунтов.

7.3. Морская турбулентность

В зависимости от соотношения сил инерции и сил вязкости, которое определяется безразмерным числом Рейнольдса, движение может идти в ламинарном или турбулентном режиме:

Re = =,

где U- характерная скорость течения, L – характерный линейный масштаб движения, ν – коэффициент кинематической вязкости.

Благодаря силам инерции частицы воды, обладающие различной скоростью движения, сближаются и возникают значительные градиенты скорости, приводящие ламинарное движение к динамической неустойчивости и образованию вихрей. Силы вязкости, наоборот, выравнивают скорости, препятствуя вихреобразованию. Таким образом, число Re характеризует соотношение дестабилизирующих движение сил инерции и стабилизирующих сил вязкости. Чем больше величина Re, т. е. чем больше преобладание сил инерции над силами вязкости, тем менее устойчиво ламинарное движение и тем больше возможности его перехода в турбулентный режим.

Переход ламинарного течения в турбулентное происходит, как показали опыты самого Рейнольдса, приблизительно при одном и том же значении числа Рейнольдса, которое на­зывается критическим. Диапа­зон критических чисел Рейнольдса довольно велик, но практическое значение име­ет наименьшая критическая величина числа Re_кр, ниже котоpогo ламинарное течение сохраняется при любых возмущениях. В качестве нижней границы критического числа Рейнольдса обычно принимают Re_кр=2000.

З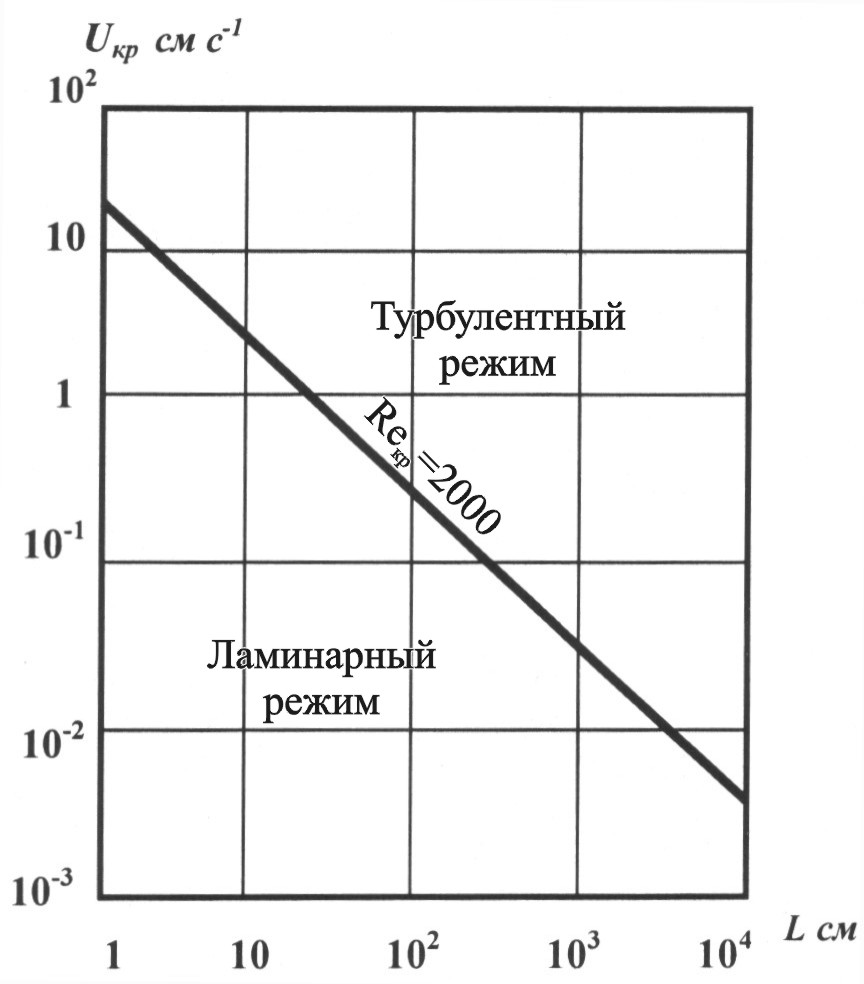ависимость между линейным масштабом потока Lи соответствующей возможной его критической скоростью Uпоказана на рис. 6. Видно, что даже максимально возможные скорости ламинарных течений весьма малы.

Рис. 6. Зависимость критической скорости ламинарного течения от его характерного линейного масштаба при Re_кр=2000

Ламинарный характер в природе носит движение грунтовых вод и, возможно, очень медленное движение водных масс во впадинах Мирового океана. Все остальные виды движения как водных, так и воздушных масс в природе турбулентны.

Критерий Рейнольдса характеризует движение в однородной по плотности среде. При наличии вертикальной плотностной стратификации переход от ламинарного режима к турбулентному зависит от особенностей распределения плотности. Для учета этой зависимости используется безразмерный критерий Ричардсона:

Ri = 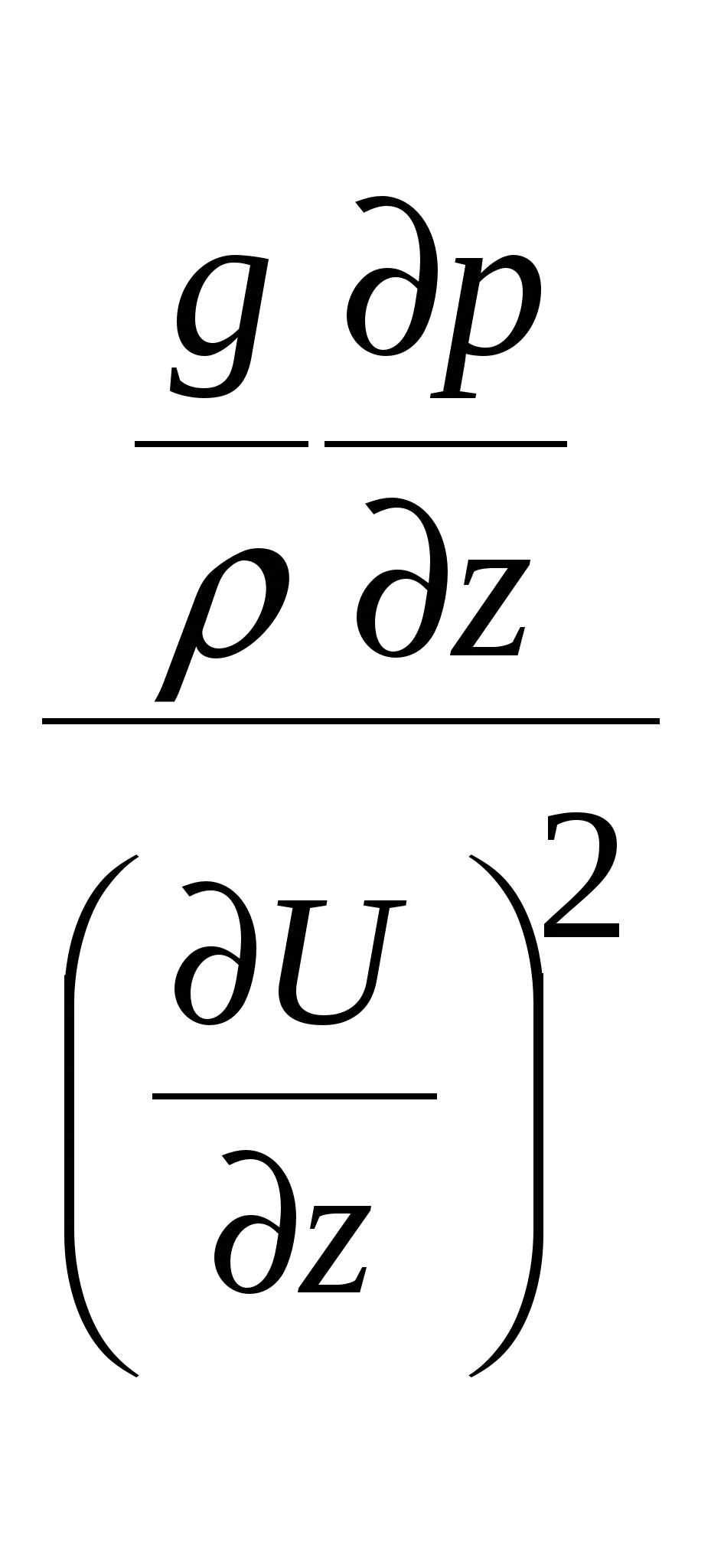, где - вертикальный градиент плотности, вертикальный градиент скорости, g – ускорение свободного падения. Числитель формулы представляет устойчивость водных слоев, которая препятствует развитию турбулентности, знаменатель – турбулизирующий сдвиг скорости, способствующий возникновению турбулентности. Поэтому, чем меньше число Ri, тем интенсивнее турбулентность и турбулентный обмен в океане.

Турбулентность в природе, характеризующаяся большими скоростями и большими линейными масштабами, представляет пример так называемой развитой турбулентности. Она возникает при обязательном наличии градиентов скорости при движении водных слоев относительно друг друга. Она может происходить как в верти­кальном, так и в горизонтальном направлениях, и существует при очень больших числах Рейнольдса и незначительных Ричардсона.

Турбулентность представляет хаотические неупорядоченные пульсации океанологических характеристик (скорости, плотности, температуры и солености воды) относительно некоторого их среднего значения, обусловленные вихревыми движениями воды, различными по длительности и масштабам.

По мере увеличения средней скорости Uв некоторый момент наступает турбулентный режимдвижения, когда в поле скорости непрерывно возникают и растут возмущения. На фоне среднего движения развиваются вихри, которые молекулярная вязкость уже не в силах погасить (рис.7).

Вихри возникают в результате динамической неустойчивости основного энергонесущего движения (волн, течения, конвекции), затем разрушаются, передавая энергию более мелким вихрям, и в конечном итоге диссипируют в тепло.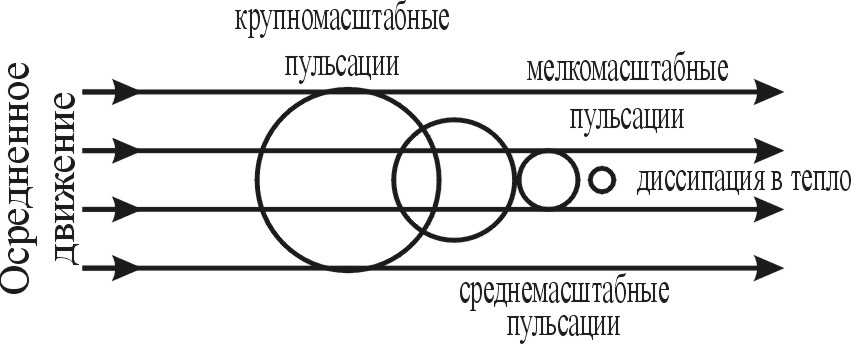



Рис.7. Передача энергии осредненного движения через пульсации различного масштаба

Вследствие непрерывного прохождения вихрей различных размеров скорость турбулентного течения в каждой точке со временем пульсирует около среднего значения (рис.8). При неоднородном поле скорости, температуры, солености и других характе­ристик их значения также беспорядочно пульсируют. По предложению Рейнольдса (1895) значения этих характеристик в точке в данный момент - мгновенные значения – можно представить в виде суммы среднего значения и пульсационного отклонения от него:

u=U+u', v =V+v', w=W+w', t=T+t', s=S+s',

где U, V, W, T, S – составляющие осредненной скорости, температуры и солености,

u', v', w', t', s' – пульсационные составляющие или пульсации этих же параметров.

Р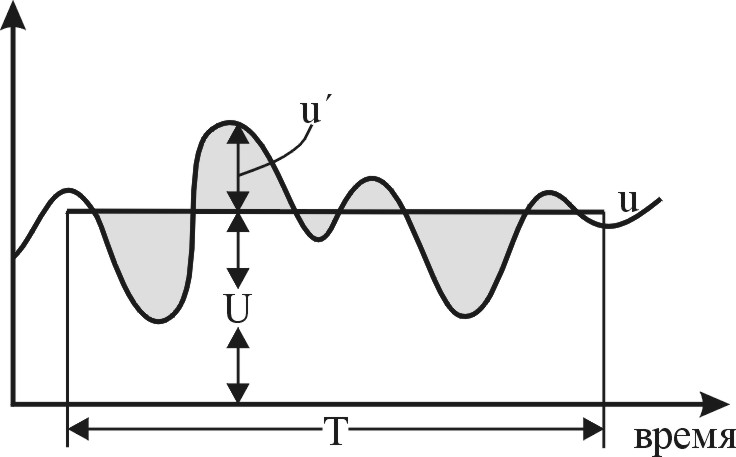ис.8. Временной ряд: мгновенные значения составляющей скорости uкак сумма осредненной скоростиUи пульсацииu'

Различают мелкомасштабную и крупномасштабную турбулентность. Основную роль в турбулентном движении играют крупномасштабные пульсации, масштаб которых соизмерим с размерами области, в которой происходит движение (в море - его глубина, толщина однородного слоя). Мелкомасштабные пульсации можно рассматривать как мелкую структуру, накладывающуюся на основные крупномасштабные движения. Основными энергетическими источниками мелкомасштабной турбулентности в верхнем слое океана являются динамическая неустойчивость ветровых волн и дрейфовых течений, на глубинах - динамическая неустойчивость внутренних волн. Мелкомасштабные турбулентные вихри размерами от нескольких метров до десятых долей сантиметра считают обычно турбулентными пульсациями скорости течения (порядка 1 см/с, в редких случаях до 10 см/с). Соответствующие пульсации температуры воды достигают 0,1⁰ С.

При развитой турбулентности осредненные за длительный промежуток времени (Т – интервал осреднения или период турбулентности) значения пульсационных составляющих равны нулю:

u'=0, v'=0, w'=0, t'=0, s'=0

Таким образом, турбулентность представляет собой статистический процесс случайных дви­жений отдельных объемов воды. Поэтому теоретическое изуче­ние турбулентности для объяснения закономерностей режима пульсационных составляющих скорости и других характеристик шло на основе приложения аппарата математической статистики. Однако развитие статистической теории турбулентно­сти сдерживалось техническими трудностями измерения пульсаций скорости, температуры, солености и других характеристик. Для удовлет­ворения нужд практики развивалась полуэмпириче­ская теория турбулентности, цель которой состояла в том, чтобы выразить характеристики турбулентности не через пульсации, а через легко измеряемые осредненные величины. Такими характеристиками являются средняя скорость потока, ее градиенты, характерные размеры потока. Для определения этих характеристик Л.Прандтль ввел в теорию турбулентности понятие о пути смешения. Путь смешения определяется как среднее расстояние, которое вихри в турбулентном потоке могут пройти, не смешиваясь с окружающей средой.

τ'=ρℓ²││.

Длина ℓ , входящая в формулу, называется длиной пути смешения.

Формула является основной в полуэмпирической теории турбулентности Прандтля, которую затем развили Дж.Тэйлор и Т.Карман. Из нее следует, что дополнительное напряжение, возникающее вследствие турбулентного перемешивания, пропорционально квадрату осредненной скорости течения.

Далее Прандтль сделал простейшее допущение относительно пути смешения, исходящее из размерности:

ℓ = æ · y,

где æ – некоторая безразмерная константа, y – расстояние от стенки (дна). Оказалось, что æ представляет универсальную константу, равную примерно 0.38-0.40. Эта константа называется постоянной Кармана.

Т.Карман в 1930 году предпринял попытку избавиться от длины пути смешения, поскольку она носит элемент неопределенности. Вместо пути смешения он рассматривал касательное напряжение и турбулентную вязкость как функцию осредненной скорости турбулентного течения. Однако при градиенте скорости, равном нулю (= 0), коэффициент турбулентной вязкости обращается в нуль, а это противоречит физической картине турбулентности. Поэтому Прандтль в 1942 году сделал новое предположение, что коэффициент турбулентной вязкости пропорционален ширине зоны перемешивания и максимальной разности осредненных скоростей, т.е.

A = ρ · æ₁ · b · (U_max – U_min),

где æ₁ – некоторое безразмерное число, которое определяется эмпирически; А – коэффициент турбулентной вязкости; b – ширина зоны перемешивания; ρ – плотность; U – осредненная скорость.

В природных условиях океана и атмосферы теория пути смешения Прандтля и гипотеза Кармана в основном применимы в пограничных слоях, где роль стенки играют поверхность Земли, взволнованная поверхность моря и дно океана.

Под пограничными слоями в природе понимаются приземной и приводный слой атмосферы; приповерхностный слой океана; придонный слой океана, влияние трения в которых о подстилающие поверхности настолько велико, что можно по сравнению с ним пренебречь влиянием отклоняющей силы вращения Земли (силы Кориолиса) на динамику течений. .

Выше приводного слоя атмосферы и ниже приповерхностного слоя моря лежат сначала так называемый "экмановский слой трения", а за ними так называемый "геострофический слой" - как в атмосфере, так и в океане. Таким образом, "слоистая" структура атмосферы и океана представляет зеркальное отображение отно­сительно поверхности моря.

Результаты полуэмпирических теорий используются для изучения потоков количества движения, тепла и влаги через поверхность моря, в частности, для иcследования касательного напряжения ветра на поверхности моря; изучения процессов испарения и теплообмена через поверхность моря; коэффициентов перемешивания в верхнем и придонном слоях моря, а также для изучения других вопросов.

7.4. Элементы статистической теории турбулентности

Представление о турбулентности, как о поле случайных значений скорости, образованном хаотическим взаимодействием вихрей разных размеров, оказалось недостаточным для дальнейшего развития теории турбулентности. Необходимы были новые критерии, позволяющие дать более подробную численную оценку процессу турбулентности.

В этом отношении значительным шагом вперед стала теория локально-изотропной турбулентности, предложенная академиком А.Н. Колмогоровым (1941) и развитая А.М.Обуховым (1941) на основании энергетических соображений. Эта теория оказала решающее влияние на развитие теории турбулентности в целом.

Физическая основа этой теории заключается в том, что рассматривается иерархия турбулентных вихрей: имеются вихри не вообще, а вихри различных линейных масштабов. При этом необходима расстановка вихрей по их масштабам для выяснения степени вклада каждого из них в энергию турбулентности. Такая расстановка вихрей по своеобразной "иерархической лестнице" выглядит следующим образом: при очень больших числах Рейнольдса на осредненный поток накладываются "пуль­сации первого порядка", проявляющиеся в беспорядочном переме­щении относительно друг друга отдельных объемов жидкости с диаметром порядка ℓ¹ = ℓ (где ℓ - прандтлевский путь перемешивания); порядок скоростей этих относительных перемещений - ν¹. Пульсации первого порядка оказываются при очень большом Re в свою очередь неустойчивыми, и на них накладываются пульсации "второго порядка" с путем перемешивания ℓ² < ℓ¹ и относительными скоростями ν² < ν¹. Такой процесс последовательного измельчения турбулентных пульсаций происходит до тех пор, пока для пульсаций какого-либо достаточно большого порядка n число Рейнольдса не окажется достаточно малым, чтобы влияние вязкости на пульсации n-порядка было уже ощутимо и предупреждало образование накладывающихся на них пульсаций (n+1)-го порядка.

Таким образом с энергетической точки зрения процесс турбулентного переме­шивания состоит из передачи энергии по каскаду турбулентных вихрей: осредненное течение заимствует энергию из атмосферных движений и передает ее энергии турбулентности; энергия больших вихрей передается энергии меньших вихрей; мельчайшие вихри благодаря вязкости диссипируют энергию в теплоту.

Развивая теорию локально-изотропной турбулентности, А.Н.Колмогоров (1941) сформулировал фундаментальные гипотезы подобия.

Первая гипотеза подобия Колмогорова. Статистические характеристики турбулентности при больших числах Рейнольдса в области малых масштабов зависят только от средней скорости диссипации энергии в единице массы жидкости ε и кинематической вязкости ν.

Вторая гипотеза подобия Колмогорова. Статистические характеристики турбулентности при больших числах Рейнольдса в области средних масштабов зависят только от средней скорости диссипации энергии в единице массы жидкости ε и не зависят от вязкости ν.

Гипотезы подобия Колмогорова разбивают спектр масштабов возмущений (или длин волн λ) в локально-изотропной турбулентности на две области: область средних масштабов, или инерционный интервал, в котором характеристики потока опреде­ляются потоком энергии по иерархии вихрей, и область малых масштабов, или вязкий интервал, в котором происходит диссипация энергии движения в тепловую энергию.

Поскольку единственными параметрами, определяющими характер локально-изотропной турбулентности, являются ε и ν, то можно определить такие важные характеристики турбулентности, как границу между инерционным и вязким интервалами, коэффициент перемешивания, плотность энергии. Так линейная граница вязкого интервала оказывается равной λ_ν = . А.М.Обухов (1962) в качестве границы вязкого интервала получил величину λ_ν = 0.37 см. Поскольку основные процессы в океане (волнение, течения и др.) связаны с турбулентностью больших масштабов, чем 0.37 см, главное внимание в теории локально-изотропной турбулентности уделяется инерционному интервалу.

Коэффициент перемешивания для инерционного интервала локально-изотропной турбулентности имеет выражение:

K = k^′ ε^1/3 λ^4/3,

где k^′ - числовой множитель порядка единицы, λ – длина возмущающей волны или масштаб турбулентности, ε - средняя скорость диссипации энергии. Эта формула представляет известный «закон четырех третей» Тэйлора-Ричардсона-Обухова.

Для инерционного интервала локально-изотропной турбулентности также важно знать, каким образом энергия турбулентности распределяется по вихрям разных масштабов. Характеристика турбулентности в этом интервале зависит от ε - средней скорости диссипации энергии и от k – волнового числа (или λ – длины волны) Поэтому в теории турбулентности рассматривается функция Φ (k) – как функция спектральной плотности энергии турбулентности между вихрями различных масштабов. Она выражается:

Φ (k) = α ε ^2/3 k^5/3,

где α – универсальная безразмерная константа, равная примерно 1.22, k = 2π/λ - волновое число соответствующего турбулентного вихря, а ε имеет порядок 10^-1 см²с^-3 для ветрового волнения, 10^-2 см²с^-3 для среднемасштабных движений и 10^-5 см²с^-3 для океанских течений. Эта формула представляет «закон пяти третей».

Зависимость самой энергии от скорости диссипации энергии и линейного масштаба турбулентности определяется формулой:

Е (λ) = α ε ^2/3 λ^2/3,

где α – универсальная безразмерная константа, определяемая опытным путем, λ – длина возмущающей волны или масштаб турбулентности, ε - средняя скорость диссипации энергии. Формула представляет «закон двух третей» Колмогорова-Обухова.

Законы «двух третей», «четырех третей», «пяти третей» описывают основные закономерности структуры локально-изотропной турбулентности. При изучении турбулентности как явления эти законы являются фундаментальными, т.е. справедливыми при самых общих положениях.

7.5. Турбулентный обмен в океане

Существенной чертой турбулентного перемешивания является то, что в процессе хаотического переноса объемов жидкости в разных направлениях помимо переноса количества движения осуществляется также перенос различных свойств жидкости: тепла, солей, взвешенных частиц, растворенных газов. Этот перенос осуществляется в направлении падения концентрации; таким образом, помимо турбулентного переноса количества движения возникает турбулентная теплопроводность и турбулентная диффузия.

Количественная оценка турбулентного переноса различных свойств жидкости была впервые дана Дж. Тэйлором (1915) и В.Шмидтом (1911, 1925). Выводы Тэйлора и Шмидта были дополнены А.В.Келлером (1930), который подчеркнул статистический характер процесса обмена и вывел формулу турбулентного обмена субстанцией через единицу площади в единицу времени

Q = - K ,

где коэффициент К называют коэффициентом турбулентного обмена субстанцией.

Под субстанцией понимается некоторая количественная характеристика жидкости, пропорциональная массе или количеству частиц в объеме. Примерами субстанции являются количество движения, количество тепла, количество солей.

Если рассматривать турбулентный поток количества движения, турбулентный поток тепла и турбулентный поток солей, то на основании предыдущей формулы можно записать:

Q_M = - K_M ; Q_T = - K_T ; Q_{S =} - K_S ,

где U – осредненная скорость, Т – температура, S – соленость, K_M, K_T и K_S – коэффициенты турбулентного обмена количеством движения, турбулентной теплопроводности и турбулентной диффузии.

Перенос субстанции турбулентным потоком приводит к изменению во времени количества субстанции в данном объеме жидкости. Для вывода закона этого изменения рассмотрим элементарный столб воды высотой δz и площадью основания, равной единице (рис. 9). Через верхнюю грань столба воды, лежащую на высоте z, за единицу времени проходит количество субстанции, равное Q = - K 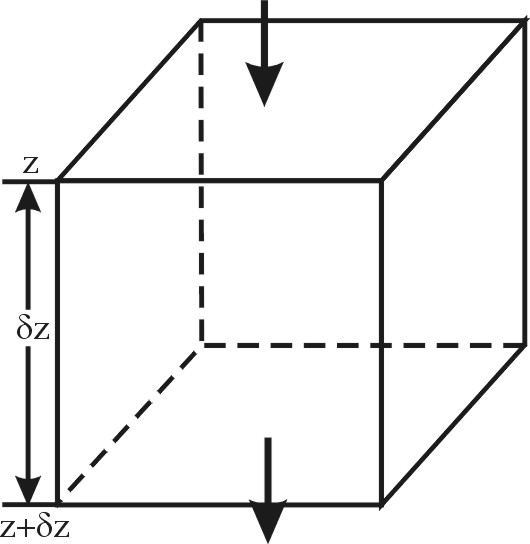, через противоположную грань, лежащую на высоте z + δz, за единицу времени проходит количество субстанции, равное Q + δQ = - K + δz

Q = - K Рис. 9. К выводу уравнения обмена. Перенос субстанции через верхнюю и нижнюю грани выделенного объема
Разность между переносом субстанции через нижнюю грань и ее переносом через верхнюю грань выделенного столба жидкости представляет изменение количества субстанции во всем рассматриваем столбе за единицу времени.


Q + δQ = - K + δz

Эта разность равна изменению в единицу времени объемной концентрации субстанции, помноженной на объем столба жидкости, т.е.

· δz · 1 = δz

Относя это изменение, совершающееся в единицу времени, к единице объема, получаем уравнение обмена:

=

Оно написано в предположении, что перемешивание осуществляется только в одном направлении z. Учитывая потоки субстанции в направлении всех трех осей – x, y, z, полное уравнение обмена выглядит следующим образом:

+U+ V+W= + +

Здесь введена запись дифференциального оператора Эйлера:

= +U+ V+W

В случае изотропного обмена, т.е. при К = const, уравнение обмена записывается сокращенно = К·Δ·q, где Δ = + + - линейный дифференциальный оператор Лапласа.

В случае, когда в качестве субстанции рассматривается количество тепла, уравнение обмена = К·Δ·q превращается в уравнение теплопроводности Фурье

= К_Т·Δ·Т,

где К_Т – коэффициент турбулентной теплопроводности

В случае, когда в качестве субстанции рассматривается количество солей, уравнение обмена = К·Δ·q превращается в уравнение диффузии Фика

= К_S·Δ·S,

где К_S – коэффициент турбулентной диффузии.

Уравнение турбулентной теплопроводности и уравнение турбулентной диффузии имеют решающее значение в физической океанологии. Вместе с уравнением состояния, уравнением неразрывности, уравнениями движения и уравнениями притока тепла и солей они составляют основу для построения замкнутой системы термогидродинамических уравнений, являющихся основой для решения различных задач динамики океана.

7.6. Устойчивость слоев в море

Рассмотрим в море частицу воды единичного объема и плотностью ρ, выведенную из состояния равновесия, т.е. смещенную под влиянием какого-нибудь импульса вниз на вертикальное расстояние dz (рис. 10).

Когда частица перемещается с меньшей глубины на большую, ее плотность увеличивается вследствие увеличения давления. Одновременно происходит уменьшение плотности вследствие повышения температуры за счет сжатия, или адиабатическое повышение температуры. Если плотность перемещенной частицы на новом уровне окажется больше плотности окружающих вод, частица будет продолжать опускаться, и наблюдается неустойчивое равновесие. Если, напротив, ее плотность окажется меньше плотности окружающих вод, частица вернется в исходное положе­ние (поднимется вверх) и наблюдается устойчивое равновесие. При равенстве плотностей частицы и окружающих вод и при отсутствии внешнего импульса вертикального движения частицы не будет, наблюдается безразличное равновесие.

Устойчивое, неустойчивое и безразличное состояние характеризуется стратификацией – вертикальным распределением водных слоев с различной плотностью. При этом устойчивое равновесие слоев в море – это когда более легкие (с меньшей плотностью) слои воды подстилаются более тяжелыми (с большей плотностью) слоями. Такая стратификация препятствует развитию перемешивания. Критерием вертикальной устойчивости служит градиент плотности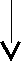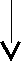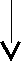. Чем больше вертикальный градиент плотности, тем больше сопротивляемость перемешиванию, тем более устойчива стратификация вод, т.е. устойчивость характеризует возмож­ность или невозможность перемешивания и его интенсивность.




ρ₁ устойчивая ρ₁ неустойчивая ρ₁ нейтральная




ρ₂ стратификация ρ₂ стратификация ρ₂ стратификация




z z z

ρ₁ < ρ₂ ; положительный; ρ₁ > ρ₂; отрицательный; ρ₁ = ρ₂; = 0

Таким образом, в неоднородном по плотности море поведение частицы будет зависеть от стратификации вод, которая может быть устойчивой (положительной - плотность с глубиной увеличивается), неустойчивой (отрицательной - плотность с глубиной уменьшается) и нейтральной (равновесной - плотность с глубиной не меняется). При устойчивой стратификации частица, смещенная вниз, будет стремиться возвратиться в исходное положение; при неустойчивой стратификации - все больше удаляться от исходного уровня; при нейтральной стратификации частица останется на исходном уровне.

Для количественной оценки условий равновесия необходимо сравнить на каком-либо уровне плотности перемещающихся по вертикали частиц и окружающих вод.

Предположим, что на глубине z, где давление Р, вода имеет соленость S, температуру Т и плотность ρ, а на глубине z+dz, где давление Р+dР, она имеет соответственно соленость S + dS и тем­пературу T+dT (рис. 9).

Р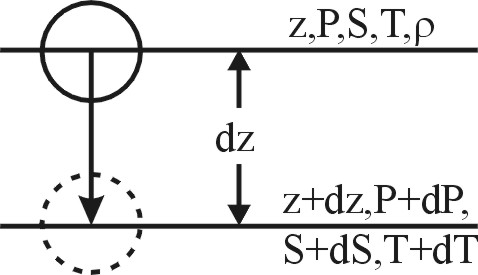ис. 10. К выводу формулы устойчивости Хессельберга-Свердрупа

Если частицу воды адиабатически переместить с глу­бины z на глубину z+dz,вследствие изменения давления ее плотность изменится за счет непосредственного воздействия давления на величину dР и на величину dξ, вызванную адиабатическим изменением температуры (при сжатии или расширении). Следовательно, на глубине z+dzплотность перемещенной с глубины z частицы будет:

ρ + dР + dξ

Окружающие массы воды на глубине z+dzбудут иметь плотность:

ρ + dР +dT +dS

Разность плотностей Δρ окружающих масс воды и перемещающихся по вертикали является критерием равновесия. Эта разность будет равна:

Δρ = ρ + dР +dT +dS – (ρ + dР + dξ)

После сокращения получим: Δρ = dT +dS - dξ

Если Δρ > 0 – равновесие устойчивое,Δρ < 0 – равновесие неустойчивое,Δρ = 0 – равновесие безразличное.

Принято определять не величину разности Δρ, а ее изменение на единицу расстояния, т. е. градиент разности =+- . Величина градиента обозначается через Е и называется вертикальной устойчивостью слоев в море. Это понятие было предложено Хессельбергом и Свердрупом в 1915 году. Не трудно видеть, что устойчивость отличается от вертикального градиента плотности только величиной адиабатической поправки . Поскольку =+, то Е= - или Е= Е_Т+ Е_S– Е_А.

Здесь Е_Т=- температурная устойчивость; Е_S=- соленостная устойчивость; Е_А= - адиабатическая устойчивость. Таким образом, под устойчивостью слоев в море понимается вертикальный градиент плотности воды, исправленный на изменения плотности, вызванные адиабатическими изменениями температуры.

Учитывая малые численные значения величины устойчивости, ее выражают в единицах Е×10⁸.

Вместо обычного выражения устойчивости в океанологии также применяется частота термохалинных колебаний, когда выведенная из состояния гидростатического равновесия частица жидкости в случае устойчивой стратификации начинает совершать колебания по вертикали относительно исходного уровня. Частота таких термохалинных колебаний в океане характеризуется критерием Вяйсяля-Брента:

N =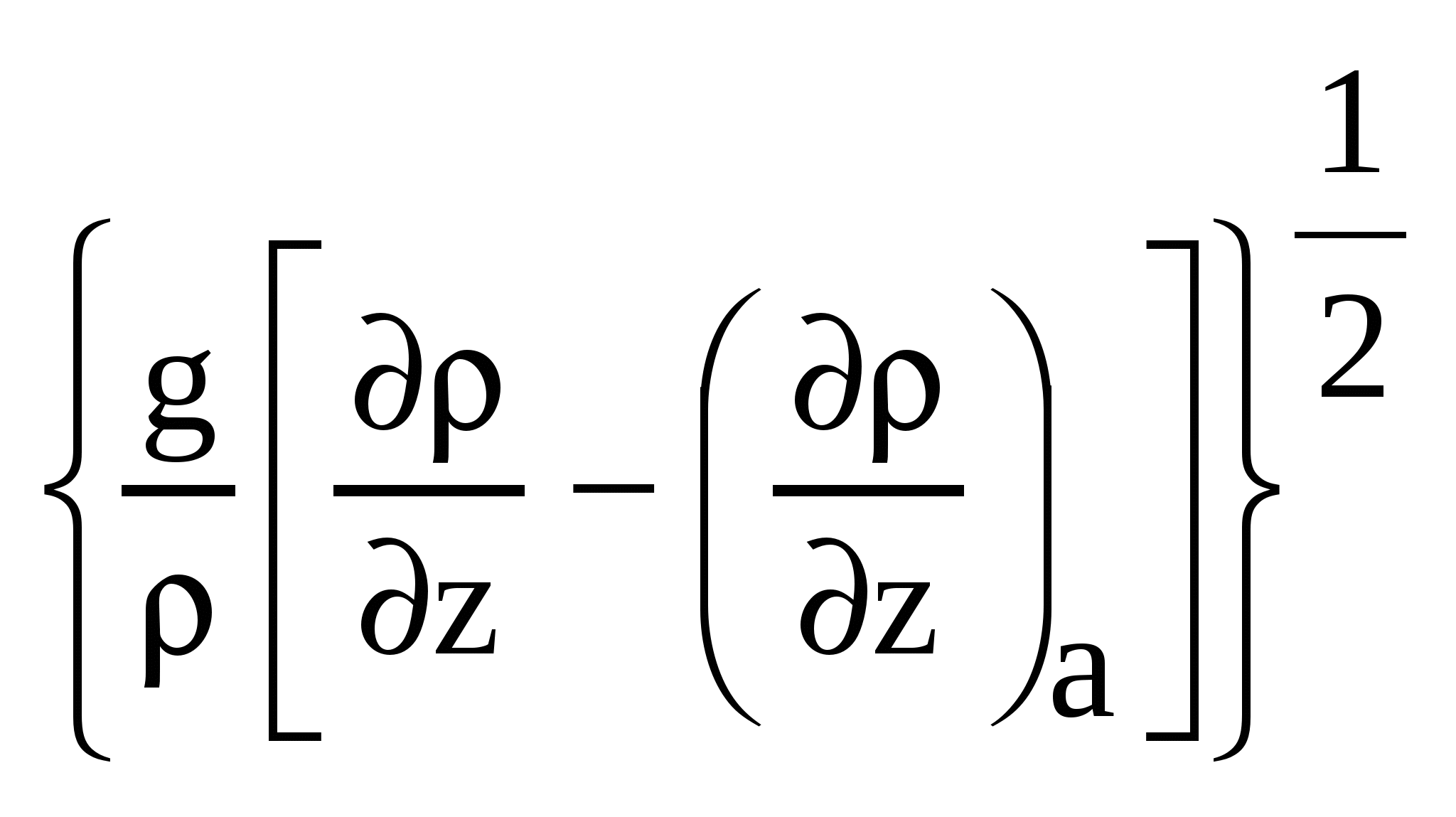, где - вертикальный градиент плотности, - адиабатическая поправка, g – ускорение свободного падения.

Термохалинные колебания тем чаще, чем больше устойчивость. В слабо стратифицированных водах эти колебания очень медленны

Выяснение устойчивости и ее измения во времени и пространстве имеют большое значение при исследовании водных масс Мирового океана. По распределению устойчивости можно судить о расположении слоя с резкими изменениями плотности - слоя скачка плотности (пикноклина), границах водных масс различного происхождения, глубине распространения конвекции и других процессах.

7.7. Конвективное перемешивание

Конвективное перемешивание или конвекция возникает при уменьшении плотности воды с глубиной, происходит оно только в вертикальном направлении и не зависит от того, находятся ли перемешиваемые слои в движении или нет. Конвективное перемешивание может наблюдаться как одновременно с турбулентным, так и независимо от него. Это перемешивание может существовать только в неоднородной, стратифицированной жидкости и представляет временное, нестационарное явление, возникающее вследствие суточного и сезонного изменения плотности воды.

Под действием тех или иных факторов в океане может происходить разрушение устойчивой стратификации, появляется однородная нейтральная стратификация, которая затем сменяется неустойчивой стратификацией вод. Появление отрицательной устойчивости приводит к тому, что более тяжелые слои воды, оказывающиеся над менее тяжелыми, увлекаются вниз под действием гравитационных сил, да­вая начало процессу вертикальной конвекции. В свою очередь конвекция одновременно выравнивает отрицательную устойчивость, и развитие конвекции сопровождается формированием однородного слоя все большей и большей толщины.

Итак, появление нейтральной, а затем отрицательной устойчивости вызывается увеличением плотности поверхностных слоев. Это увеличение плотности происходит либо за счет уменьшения температуры, либо за счет увеличения солености, либо за счет совместного изменения этих характеристик. В первом случае начинается термическая конвекция, во-втором - с соленостная конвекция; наконец, когда происходит одновременное изменение температуры и солености, то происходит процесс термохалинной конвекции. Если изменения температуры и солености чередуются или вперед выступает один из факторов (например, увеличение солености), то можно говорить о термической и соленостной стадиях в общем процессе.

Иногда увеличение плотности (уплотнение при смешении) может наблюдаться в результате смешения вод различной солености и температуры при турбулентном перемешивании.

Уменьшение температуры, вызывающее увеличение плотности поверхностных слоев, происходит за счет теплоотдачи в атмосферу при охлаждении моря в осенний и зимний периоды.

Увеличение солености происходит либо за счет осолонения по­верхностных слоев при испарении, либо за счет осолонения при льдообразовании.

Эти три фактора - охлаждение, испарение и осолонение поверхностных слоев моря проявляют свое действие в разных климатических условиях и в разные сезоны, вызывая процессы вертикальной конвекции различной интенсивности и различного масштаба. .

Характер термической конвекции зависит от того, происходит ли она в морских водах, т.е. при солености выше 24,695‰,или в солоноватых водах, когда соле­ность меньше 24,695‰. В первом случае температура наибольшей плотности совпадает с температурой замерзания, и нижним пределом уменьшения температуры является температура замерзания. После достижения слоями воды температуры замерзания, дальнейшее увеличение плотности происходит за счет осолонения воды при льдообразовании. Таким образом, процесс соленостной конвекции естественно следует за термической конвекцией.

В случае солоноватых вод процесс термической конвекции прекращается по достижении температуры наибольшей плотности, которая в этом случае выше температуры замерзания, поскольку при дальнейшем понижении температуры вновь возникает устойчивая стратификация. Следовательно, соленостная стадия конвекции не может непрерывно следовать за термической стадией, и для дальнейшего продолжения конвекции необходимы особые условия.

В природных условиях конвективное перемешивание может происходить как за счет раздельного изменения температуры и солености, так и за счет их суммарного воз­действия. В зависимости от причин, вызывающих конвекцию, и географического расположения районов, в котором она наблюдается, выделяют следующие типы конвективного перемешивания.

1. Арктический тип. Конвекция происходит преимущественно за счет осолонения при льдообразовании. Такое перемешивание характерно для замерзающих морей, в которых годовая амплитуда температуры мала, а льдообразование велико (пример - Арктический бассейн Северного Ледовитого океана).

2. Полярный тип. Конвекция происходит сначала за счет понижения температуры, затем за счет повышения солености при льдообразовании. Характерна для морей высоких широт с положительным пресным балансом и большой амплитудой температур (Белое и Карское моря).

3. Субполярный тип. Конвекция развивается только вследствие понижения температуры. Этот тип ха­рактерен для морей умеренных и высоких широт, в которых нет льдообразования и где пресный баланс близок к нулю, вертикальные градиенты солености также близки к нулю, а годовые амплитуды поверхностной температуры велики (юго-западная часть Баренцева моря).

4. Субтропический тип. Конвекция возникает в результате повышения солености при испарении и понижении температуры. Характерна для морей с отрицательным пресным балансом и большой амплитудой температуры. Примером является Средиземное море. Летом соленость на его поверхности увеличивается, так как испарение преобладает над осадками и стоком с суши. Однако конвекции благодаря повышению температуры не происходит. С наступлением зимы при охлаждении поверхностного слоя моря развивается интенсивное конвективное перемешивание, распространяющееся додна.

5. Тропический тип. Конвекция возникает за счет повышения солености при испарении. Этот тип перемешивания характерен для тропических морей, в которых пресный баланс отрицателен, а годовые амплитуды температуры и солености малы (Красное море).

В большинстве районов Мирового океана наиболее интенсивное конвективное перемешивание происходитв результате охлаждения поверхностных слоев в холодную половину года. Этот вид перемешивания получил специальное название - зимняя вертикальная циркуляция. Ее интенсивность и глубина распространения тем больше, чем интенсивнее и продолжительнее процесс охлаждения поверхностных слоев воды зимой.

В результате перемешивания в поверхностном слое воды толщиной от нескольких десятков досотен метров образуется изотермический слой с температурой, соответствующей температуре на поверхности (гомотермия).

Ниже перемешавшегося слоя будет находиться слой, не охваченный зимней вертикальной циркуляцией, на границе с которым будет отмечаться более или менее резко выраженный скачок температуры. При этом в зависимости от вертикального распределения солености температура слоя, не охваченного перемешиванием, может быть выше или ниже вышележащего.

Для расчета глубины зимней вертикальной циркуляции и температуры после перемешивания необходимо знать начальное вертикальное распределение температуры и солености воды и количество тепла, отдаваемое поверхностью моря.

Глубина, до которой доходит конвективное перемешивание лишь за счет термической стадии (без льдообразования) была названа Н.Н.Зубовым критической глубиной конвекции (зимней вертикальной циркуляции). Количество тепла, отдаваемое одним квадратным сантиметром поверхности моря для достижения кри­тической глубины, Н.Н.Зубов назвал показателем замерзания, а количество тепла, необходимое для достижения конвекцией дна (без льдообразования), - показателем вентиляции.

С началом прогрева поверхностных слоев в теплую половину года холодный слой воды, образовавшийся в процессе зимней вертикальной циркуляции, исчезает не сразу, а по мере передачи тепла в глубину. В результате на некоторой глубине сохраняется холодный промежуточный слой, который в случае недостаточно интенсивного прогрева в теплую половину года может существовать доначала нового зимнего охлаждения.

Так как с вертикальным распределением температуры связаны многие процессы, протекающие в океане (морские течения, распространение звука и др.), то конвективное перемешивание и, в частности, зимняя вертикальная циркуляция играют существенную роль в гид­рологическом режиме океанов и морей.