Дискретная математика. ДМ. Министерство образования республики беларусь
 Скачать 107.85 Kb. Скачать 107.85 Kb.
|
|
X представляют интервалы булева пространства аргументов. В матрице Yединица в столбце fi и j-й строке показывает, что на всем j-м интервале функция fi имеет значение 1 (j-я конъюнкция входит в ДНФ функции fi). Рассмотрим теперь выполнение второго этапа минимизации, который сводится к задаче покрытия. Пара одноименных строк матриц X и Y представляет множество пар вида (mi, fj), где mi – элемент булева пространства аргументов, а fj – функция, принимающая значение 1 на этом элементе. Интервал и его характеристика являются сомножителями декартова произведения, результат которого представляет собой множество с элементами вида (mi, fj). Очевидно, всего пар вида (mi, fj) в задании системы булевых функций столько, сколько единиц в исходной матрице функций. Необходимо из полученной совокупности интервалов выбрать минимум так, чтобы выбранные интервалы со своими характеристиками покрыли все множество пар (mi, fj) в задании исходной системы. Для решения рассматриваемого примера построим следующую матрицу, строкам которой соответствуют пары строк матриц X и Y, а столбцам – пары вида (mi, fj):
Здесь надо выбрать минимальное количество строк так, чтобы каждый столбец имел единицу хотя бы в одной из них. Искомое кратчайшее покрытие составляют строки с номерами 1,3,4,5,6,7, а минимальная система ДНФ представляется матрицами:
Задача 3 Закодировать методом «желательных соседств» состояния автомата и получить соответствующую минимальную систему ДНФ:
Решение Абстрактным автоматом называется система S={A, Z, W, , , a1}, где A={a1, ..., aМ} – алфавит состояний, Z={z1, ..., zF} – входной алфавит, W={w1, ..., wG} – выходной алфавит, – функция переходов, –функция выходов, a1 – начальное состояние автомата. Поскольку функции и определены на конечных множествах, то их можно задавать таблицами, обычно две таблицы объединяют в одну x: ZxA ZxW, называемой таблицей переходов автомата. Автомат S называется частичным, или не полностью определенным автоматом, если хотя бы одна из его двух функций не полностью определена, т.е. для некоторых пар (состояние, вход) значение функции или обе функции не определены. В автоматной таблице неполная определенность автомата выражается в том, что некоторые ее клетки незаполненные. Задача кодирования состояний является одной из основных задач канонического метода структурного синтеза автоматов. Суть кодирование заключается в установлении взаимно-однозначного соответствия между множеством A={a1, ..., aМ} состояний автомата и множеством R-компонентных векторов {К1,…, КM), КM=(еM1,…,eMR}, где еMR, - состояние r-го элемента памяти r=1,…,R. Если при переходе автомата из одного состояния в другое должны изменить свои состояния сразу несколько запоминающих элементов, то между ними начинаются состязания, или гонки. Для обеспечения заданного закона функционирования автомата необходимо исключить возможность появления критических гонок. Наряду с аппаратными методами, существуют и логические методы, одним из которых является кодирование методом «желательных соседств». Суть этого метода заключается в том, что соседние состояния автомата кодируются наборами, различающимися состоянием только одного элемента памяти. Существует несколько алгоритмов соседнего кодирования. Соседнее кодирование, однако, не всегда возможно. Учитывая, что в задании не требуется проверить наличие возможности такого кодирования, то буде считать что оно возможно. Согласно заданию элементом памяти является JK-триггер. JK-триггер – это асинхронный двухступенчатый триггер, он имеет два информационных входа. Таблица определяет переходы JK-триггера согласно логической формулы 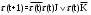 Состояния JK-триггера.
Возможны следующие режимы работы JK-триггера: J=0, K=0 – режим хранения информации (значение триггера не изменяется); J=0, K=1 – режим сброса (триггер всегда устанавливается в 0); J=1, K=0 – режим записи логической единицы (триггер устанавливается в 1); J=1, K=1 – режим инверсии содержимого триггера. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
