Министерство образования РФ сибирский государственный технологический университет
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
Wр(p) =W1-4(p)W5-7(p),Подставим числовые значения в выражение (1.1): . Находим передаточную функцию для замкнутой цепи с обратной единичной связью: Wп(p) =W6(p)W5-7(p) Подставим числовые значения в выражение (1.2): 2 Исследование системы на устойчивость 2.1 Критерий Гурвица Чтобы система была устойчивой необходимо и достаточно, чтоб главный определитель матрицы Гурвица и все его диагональные миноры были не отрицательны. Критерий Гурвица предполагает исследование замкнутой системы по ее характеристическому многочлену: |
| а0 | а2 | а4 | а6 | |
| а1 | а3 | а5 | a7 | |
| a     1a2-a0a3 1a2-a0a3b1= a1 | а1a4-a0a5 b2= a1 | a1a6-a0a7 b3= a1 | а1a8-a0a9 b4= a1 | |
| b     1a3-a1b2 1a3-a1b2c1= b1 | b1a5-a1b3 c2= b1 | b1a7-a1b4 c3= b1 | b1a9-a1b5 c4= b1 | |
| c     1b2-b1c2 1b2-b1c2d1= c1 | с1b3-b1c3 d2= c1 | c1b4-b1c4 d3= c1 | c1b5-b1c5 d4= c1 | |
| | | | | |
Выписываем характеристический многочлен и вычисляем коэффициенты таблицы Рауса:
Таблица 2 - Коэффициенты таблицы Рауса
| 7,36*10-4 | 0,332 | 14,175 |
| 3,008*10-2 | 1 | 0 |
| 0,308 | 14,175 | 0 |
| -0,386 | 0 | 0 |
| 14,175 | 0 | 0 |
Вывод: Данная система в замкнутом состоянии является не устойчивой, т.к. не все коэффициенты первого столбца таблицы Рауса положительны.
2.3 Критерий Михайлова
Для устойчивости АСР n-го порядка необходимо и достаточно, чтобы годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости, обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль.
Выписываем характеристическое уравнение замкнутой АСР:

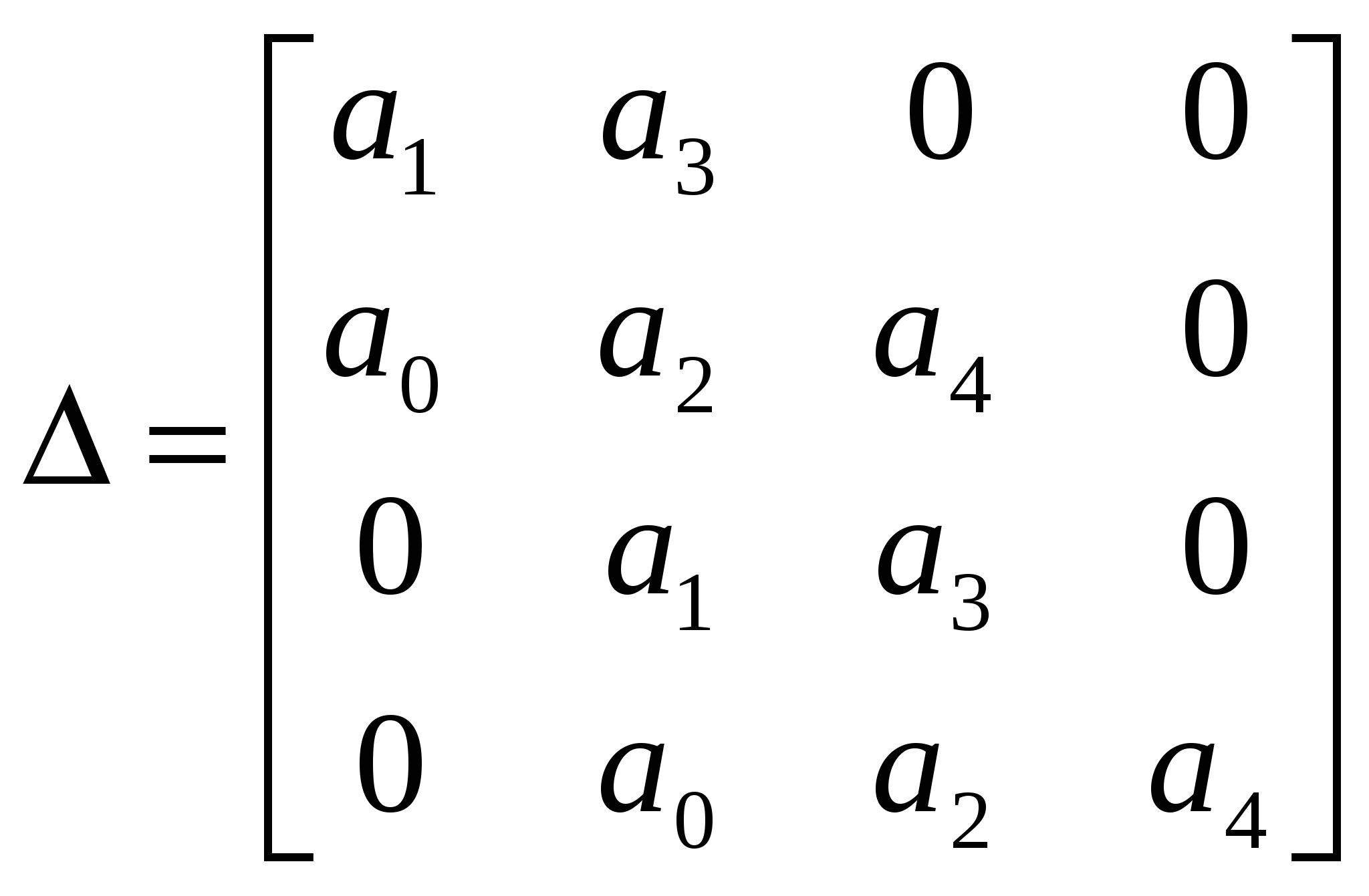 .
. 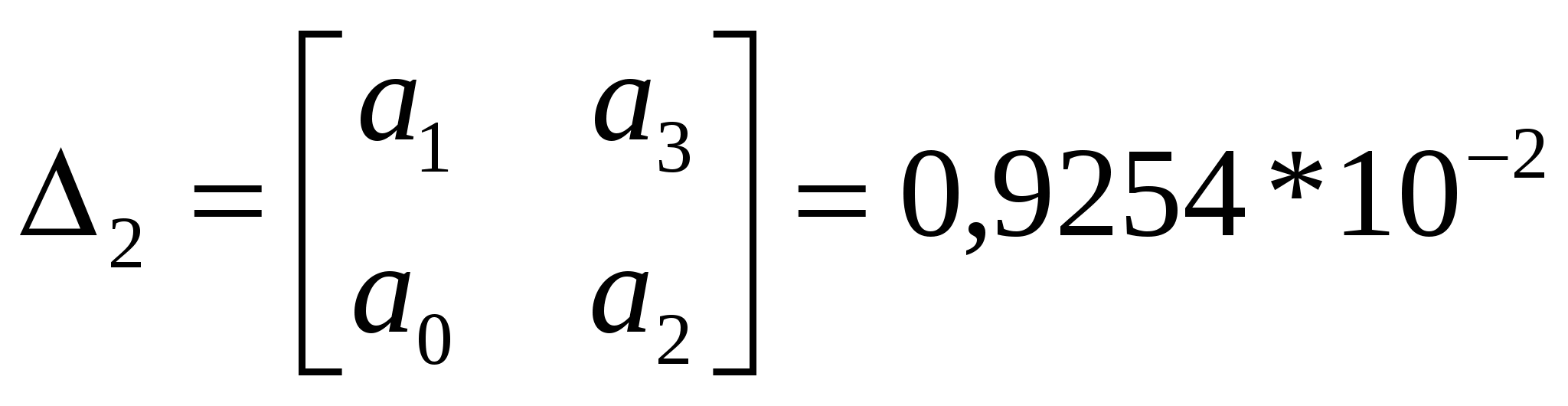 ,
,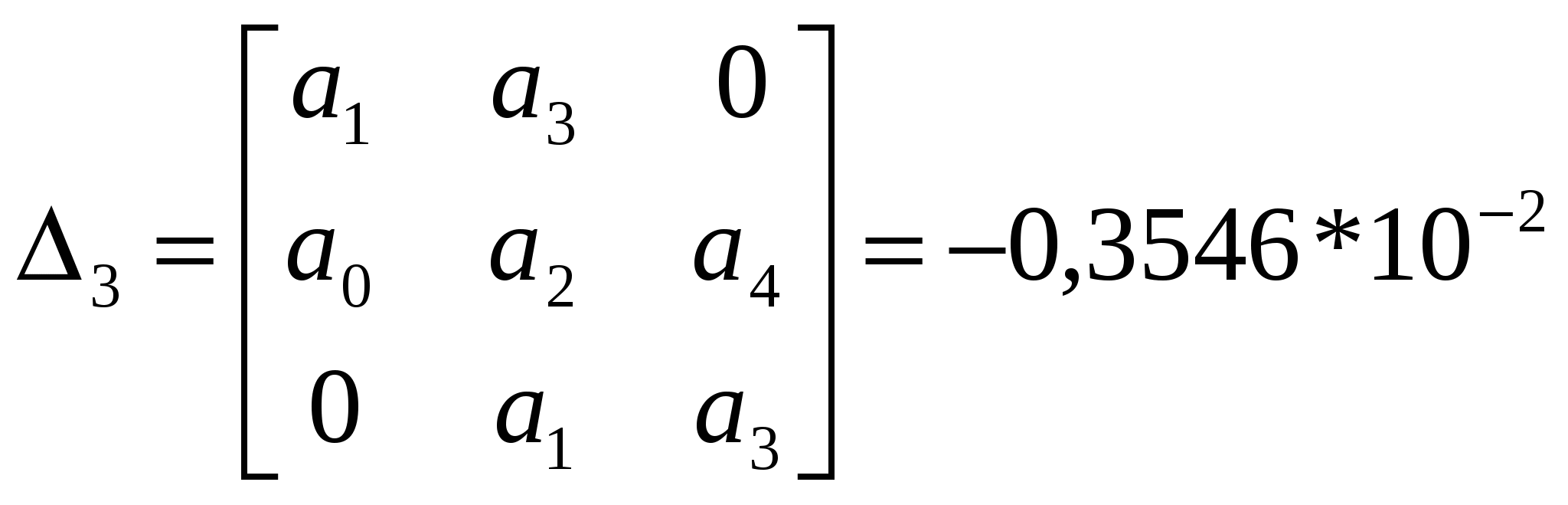 ,
,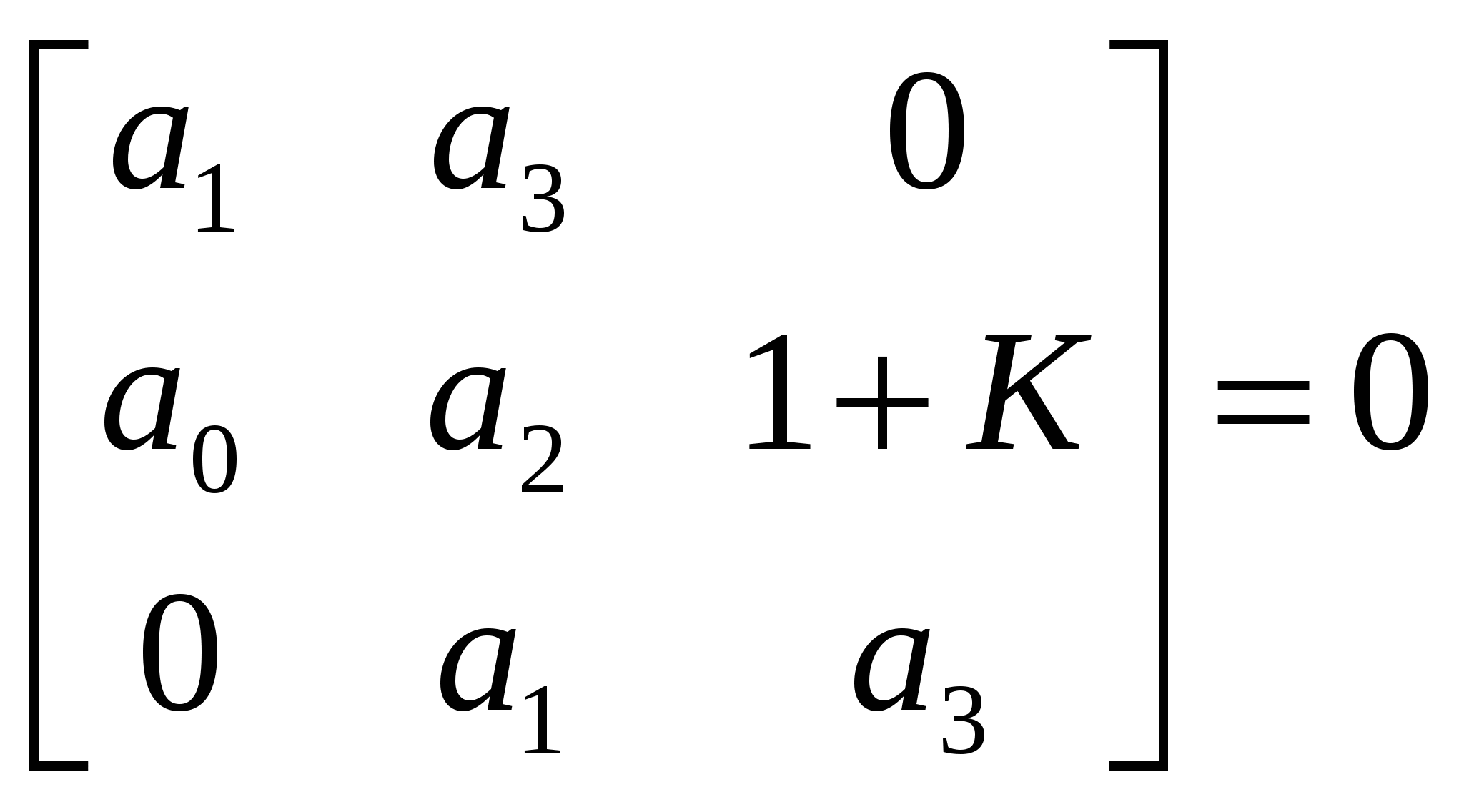 (1.3)
(1.3)