Министерство образования РФ сибирский государственный технологический университет
 Скачать 1.32 Mb.
|
3 Синтез линейной системы автоматического регулирования по логарифмическим частотным характеристикам3.1 Построение желаемых логарифмических характеристик Желаемой называют асимптотическую ЛАЧХ Lж() разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ (рисунок 11) состоит из трёх основных асимптот: низкочастотной, среднечастотной и высокочастотной. Кроме того, могут быть сопрягающие асимптоты, которые соединяют основные. Построение желаемой ЛАЧХ производится на основании требований к системе. Низкочастотная часть этой характеристики обуславливает точность воспроизведения медленно изменяющихся воздействий. По её виду можно найти добротности по скорости и ускорению и статическую ошибку системы. Низкочастотный участок (рисунок 11) для астатических систем (неизменяемая часть системы L0() ) должен иметь наклон –20n дб/дек (где n – число интегрирующих звеньев в системе, в нашем случае n = 1) и при = 1 ординату, равную 20lgK (для нашего случая 20lgK=23.03, где К = 14.175). Среднечастотная асимптота ЛАЧХ разомкнутой системы и её сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики. Построение среднечастотной асимптоты желаемой ЛАЧХ начинаем с выбора частоты среза СР по номограмме составленной В.В.Солодовником ([1], страница 272), которая определяет зависимость перерегулирования и времени регулирования tР от максимума РMAX вещественной частотной характеристики замкнутой системы, причём время регулирования tР дано в виде функции частоты среза СР. По заданному значению перерегулирования = 25% определяем значение РMAX = 1,18. Затем по РMAX определяем соотношение между tР и СР:  .  с-1.Среднечастотная асимптота желаемой ЛАЧХ проводится через точку СР с наклоном -20дб/дек. При большем наклоне трудно обеспечить необходимый запас устойчивости и допустимое перерегулирование. Проводим прямые с ординатами +∆L и -∆L (пунктирными линиями на рисуноке 11). Затем после построения среднечастотной асимптоты (наклон –20 дб/дек) наносим сопрягающую асимптоту с наклоном –40 дб/дек, начиная её из точки среднечастотной асимптоты с ординатой ∆L = 20 дб. Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства системы, поэтому выбираем (наклон –40 дб/дек) её так, чтобы корректирующее устройство было возможно более простым. Это достигается при совмещении высокочастотных асимптот характеристик Lж() и L0(). 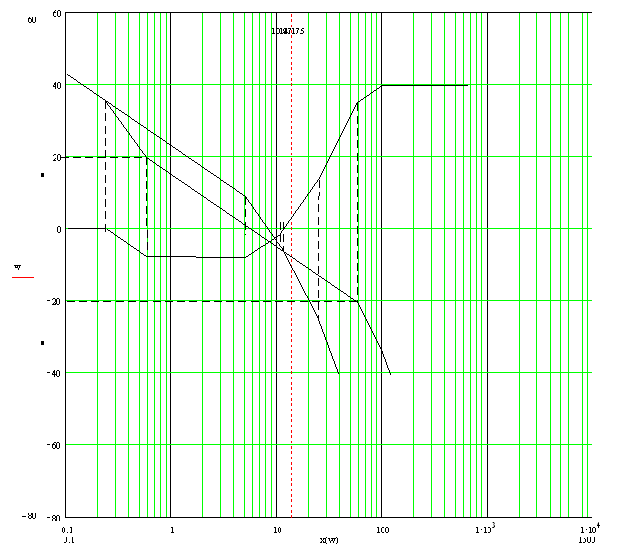 Рисунок 10 - Построение желаемой ЛАЧХ и ЛАЧХ корректирующего устройства 3.2 Определение передаточной функции желаемой ЛАЧХ По виду желаемой ЛАЧХ Lж() составляем передаточную функцию разомкнутой скорректированной системы:  , (3.2.1) где  . (3.2.2)По формуле (3.2.2) определяем постоянные времени Та, Тв, Те, Тf Та = 1.724, Тв = 0.017, Те = 4.651, Тf = 0.01 Подставив в формулу (3.1.1) коэффициенты получим  . Проверяем избыток фазы при контрольных частотах а = 0.58 с-1 , СР = 5.9 с-1 и b = 58 с-1 (рисунок 11) по следующей формуле: ∆  = π +  , (3.1.3)где  ,< 0. Проверяют запас устойчивостиΔφж(ωа ) и Δφж(ωв ) на частотах ωаиωв , граничных частотах среднечастотного диапазона.Еслиусловие Δφ≥Δφmin (Δφmin=500=0,873 рад) выполняется, то система имеет требуемый запас по фазе, и выполненное сопряжение асимптот желаемой ЛАЧХ принимается.  , рад,∆  ( а) = 1,115 рад ,∆ (а) > ∆ min . ,∆ (b) = -0,532 рад,∆ (b) < ∆min .Условие запаса устойчивости выполняется только для частоты  .Тогда проверим выполнение данного условия на частоте среза  .Подставив численные значения, получим  ,условие выполняется, значит, вопрос о коррекции желаемой ЛАЧХ, решаем на основе оценки качества системы.3.3 Расчет переходного процесса по вещественной частотной характеристике методом трапеций Наиболее известным методом определения переходных процессов является метод построения кривой переходного процесса с помощью трапецеидальных вещественных частотных характеристик АСР. 1) Записываем передаточную функцию замкнутой системы на основе передаточной функции скорректированной разомкнутой системы  ,  .2) Вычисляем коэффициенты этой передаточной функции:  , где  ; ; ; ; ; ; ; .Передаточная функция скорректированной замкнутой системы с учётом найденных коэффициентов имеет следующий вид:  .3) Выделяем вещественную частотную характеристику замкнутой системы, произведя следующую подстановку:  ,  .Записываем значения вещественной и мнимой части для полиномов числителя и знаменателя частотной передаточной функции замкнутой АСР:  , где  ; ; ; .Записываем значение вещественной частотной характеристики для замкнутой системы:  ,  .Задавая значения 0 < < 70 (таблица 6), строим вещественную частотную характеристику (рисунок 11). Таблица 6 – Значения вещественной характеристики
 Рисунок 11 – Вещественная частотная характеристика 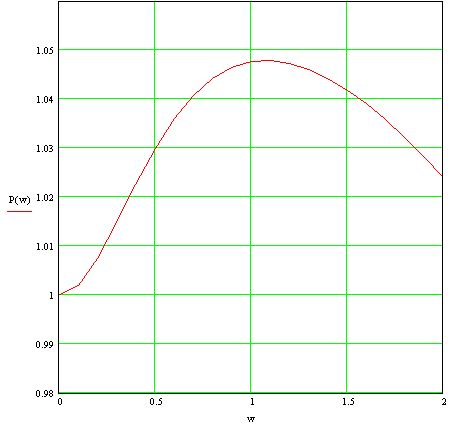 Рисунок 12 – Увеличенный участок ВЧХ 4) Разбиваем вещественную частотную характеристику на трапеции. Для этого кривую вещественной характеристики заменяем приближенно трапециями (рисунок 13 – 14) с учетом следующих правил:
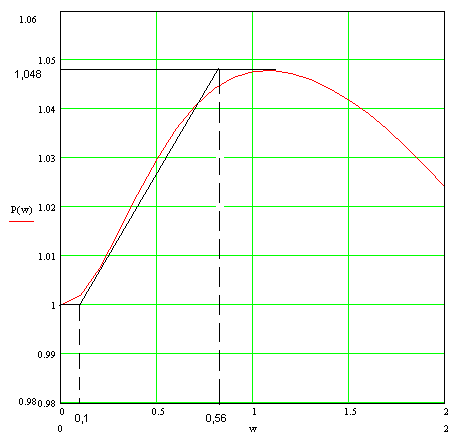 Рисунок 13 – Разбиение ВЧХ на трапеции  Рисунок 14 – Разбиение ВЧХ на трапеции
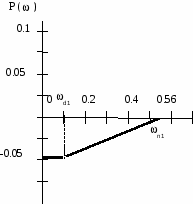 Рисунок 15 – Трапеция № 1 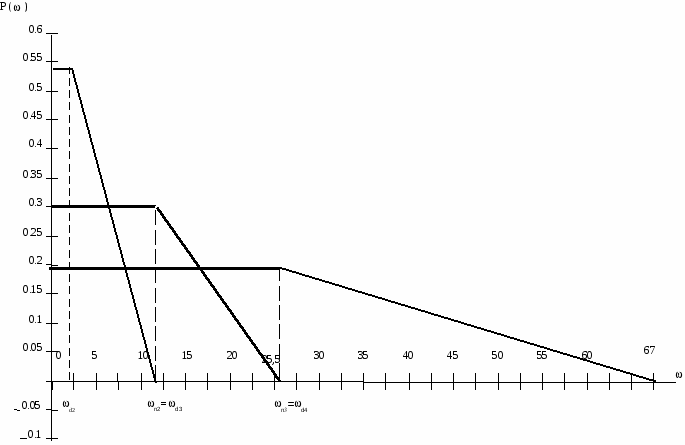 Рисунок 16 – Трапеции № 2, 3, 4
Продолжение таблицы 7
6) По параметрам трапеции определяем составляющие переходной характеристики. Для каждой трапеции в таблице h – функций ([1], страница 222) отыскиваем столбец, соответствующий значению коэффициента наклона . Для ряда значений условного времени определяем соответствующие им значения h(). По значениям и h() вычисляем значение действительного времени и соответствующие hi переходной характеристики:  ;  (3.1.12)Полученные значения t и hi заносим в таблицу 7. 7) Строим графики составляющих переходной характеристики (рисунок 17). 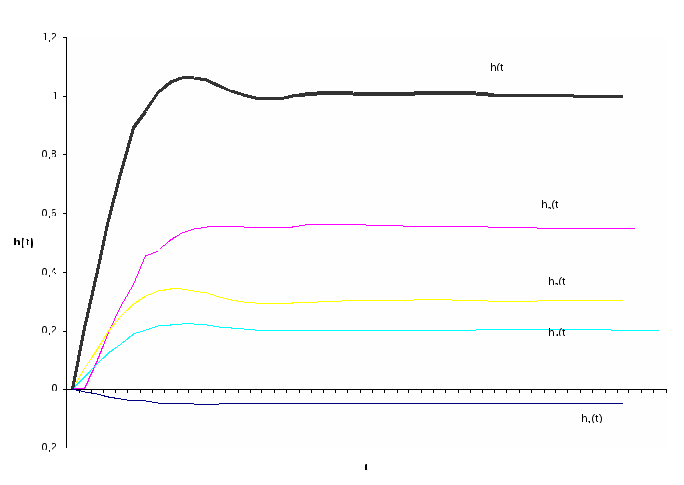 Рисунок 17 - Графики составляющих переходной характеристики 8) Строим график переходной характеристики (рисунок 18). Ординаты переходной характеристики определяем суммированием ординат составляющих в выбранные моменты времени. 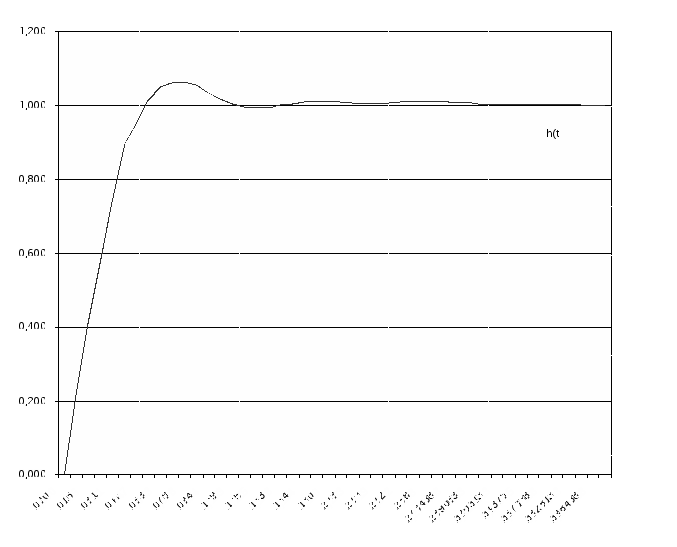 Рисунок 18 - График переходной характеристики | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||