Министерство образования РФ сибирский государственный технологический университет

• Название: Министерство образования РФ сибирский государственный технологический университет
• Анкор: TAU_KRR_12-9-1.doc
• Дата: 27.08.2018
• Размер: 1.32 Mb.
• Имя файла: TAU_KRR_12-9-1.doc
• Тип: Пояснительная записка; #23622
• страница: 4 из 6

Производим подстановку р = (j):

7,36*10^-4(j)⁴+3,008*10^-2(j)³+ 0,332(j)²+ (j)+ 14,175 = 0.

Выделяем вещественную и мнимую часть многочлена:
P() + jQ() = (7,36*10^-4⁴ – 0,332²+14,175) + j( - 3,008*10^-2³).
Задаём значения 0     и считаем P(), Q():
Таблица 3 - Данные для построения годографа Михайлова

	0	1	4	8	16	20	24
P()	14,175	13,844	9,051	-4,058	-22,58	-0,865	67,13
Q()	0	0,97	2,075	-7,4	-107,2	-220,6	-391,8
	28	32	36	40	60	∞
P()	206,27	445,96	820,1	1367,1	8357,5	+∞
Q()	-632,3	-953,7	-1367	-1885	-6437	-∞

По данным таблицы 3 строим годограф Михайлова (рисунок 3).


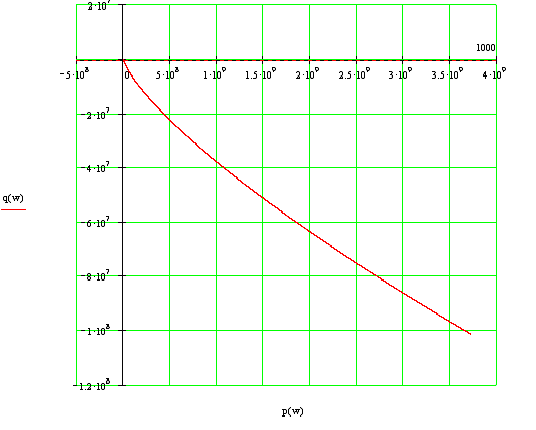
Рисунок 3 - Годограф Михайлова


Рисунок 4 - Увеличенный участок на годографе Михайлова



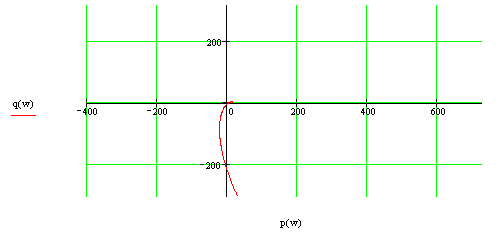
Рисунок 5 - Увеличенный участок на годографе Михайлова



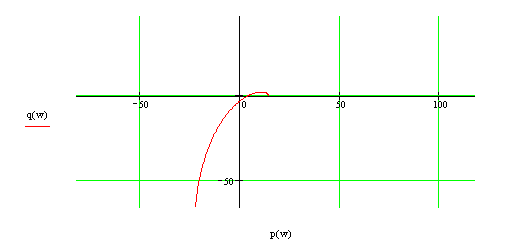
Рисунок 6 - Увеличенный участок на годографе Михайлова
Вывод: Данная система в замкнутом состоянии является не устойчивой, т.к. годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости (рисунок 4 – 6), обошёл в положительном направлении (против часовой стрелки) лишь 3 квадранта.
2.4 Критерий Найквиста
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутого контура САР.

Записываем передаточную функцию разомкнутой АСР:
. (1.4)
Делаем замену р = (j) и подставляем в уравнение (1.4):
.

Выделяем в знаменателе действительную и мнимую часть и домножаем на сопряженное:

.
Выписываем вещественную и мнимую части:
,
.
По данным таблицы 4 строим годограф Найквиста (рисунок 4).
Таблица 4 - Данные для построения годографа Найквиста

	0	2	4	6	10	20	30	40
P()	0	-3,865	-2,337	-1,286	-0,342	-0,004	0,006	0,003
Q()	0	-5,166	-0,963	0,058	0,266	0,064	0,016	0,005
	50	60	70	140	150	∞	60	60
P()	0,002	0,0012	0,0006	0,00005	0,00004	+0	0,0012	0,0012
Q()	0,0018	0,0008	0,0004	0,00001	0,00001	-0	0,0008	0,0008

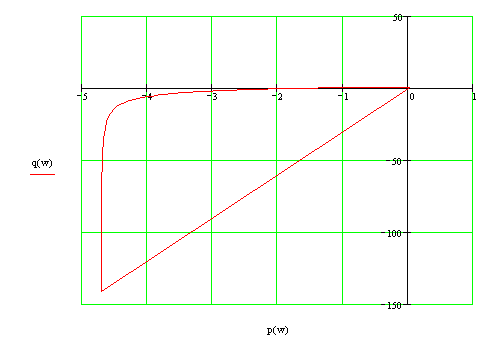
Рисунок 7 - Годограф Найквиста





Рисунок 8 - Увеличенный участок годографа Найквиста
Вывод: Разомкнутая система является не устойчивой, т.к. АФЧХ (рисунок 7 – 8) системы охватывает точку с координатой (-1,j0).

2.5 Логарифмический критерий
Записываем передаточную функцию разомкнутой системы:
.
Определяем значения сопрягающих частот:
, , . (1.4)
, , .
ω_к=к₁к₂к₃к₄к₅ , ω_к=14,175
Фазочастотная характеристика разомкнутой системы:

суммарная

(1.5)

для каждого звена

;

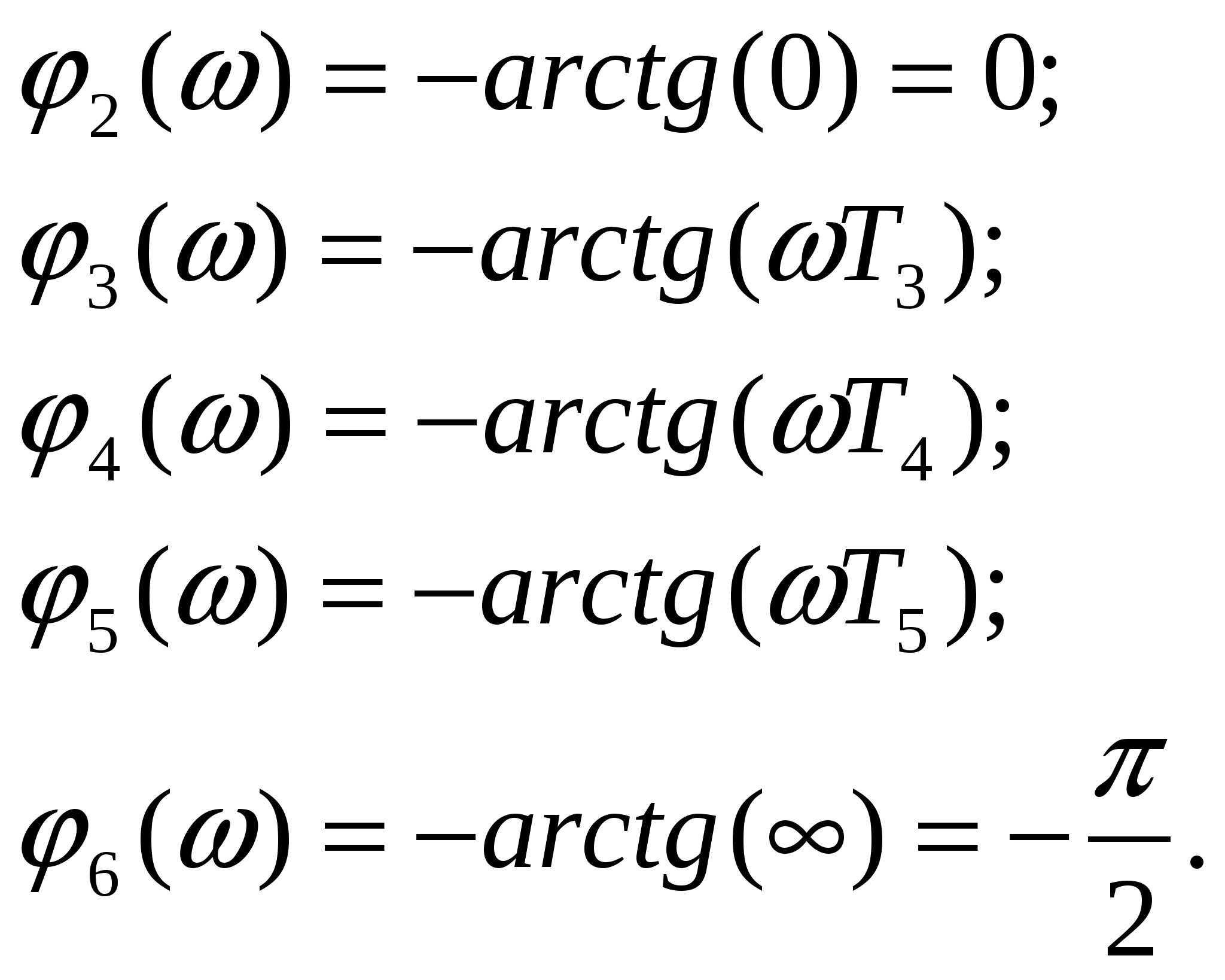(1.6)

Используя формулы (1.4), (1.5), (1.6) заполняем таблицу 5.
Таблица 5 - Данные для построения ЛФЧХ разомкнутой системы

	3	4	5	
0	0	0	0	-1,57
1	-0,197	-0,092	-0,04	-1,9
5	-0,785	-0,431	-0,197	-2,985
10	-1,107	-0,744	-0,381	-3,802
10,87	-1,14	-0,785	-0,41	-3,906
25	-1,373	-1,161	-0,785	-4,89
100	-1,521	-1,463	-1,326	-5,88
1000	-1,566	-1,56	-1,546	-6,242

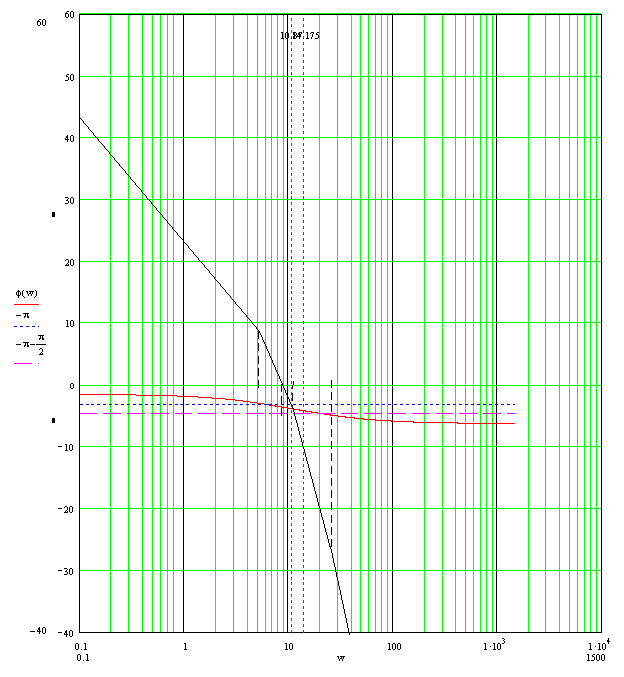
Рисунок 9 - Логарифмическая частотная характеристика разомкнутой системы
Вывод: Система является астатической, т.к. в передаточной функции разомкнутой системы присутствует интегрирующее звено. Из логарифмических частотных характеристик разомкнутой системы (рисунок 9) видно, что система не устойчива.