Минобрнауки науки РФ
 Скачать 128.2 Kb. Скачать 128.2 Kb.
|
                           МИНОБРНАУКИ НАУКИ РФ РГУ нефти и газа (НИУ) имени И.М. Губкина
КУРСОВАЯ РАБОТА
Вариант 8
Оглавление1. Введение 3 2. Основные сведения из теории упругости 5 5. Литература 24 1. ВведениеВариационный метод — метод решения математических задач с помощью минимизации определённого функционала, используя пробную функцию, которая зависит от небольшого количества параметров. Вариационные методы решения задач теории упругости, основаны на различных вариационных принципах, из которых наиболее известен принцип Лагранжа. Принцип Лагранжа известен студентам из курсов сопротивления материалов и строительной механики. Он используется при выводе интеграла Мора для определения перемещений стержневых систем, доказательства теоремы Бетти о взаимности работ, вывода системы канонических уравнений метода сил при расчете статически неопределимых стержневых систем. Строгое доказательство принципа Лагранжа и других вариационных принципов теории упругости может быть проведено методами вариационного исчисления, специального раздела математики. 2. Основные сведения из теории упругостиЗадачей теории упругости является определение напряженно-деформиро- ванного состояния упругого тела, т.е. определение полей напряжений и дефор- маций в упругом теле, возникающих под действием внешних сил. В теории упругости предполагается, что исследуемое тело обладает свой- ствами сплошности, однородности, изотропности и упругости. Свойство с п л о ш н о с т и состоит в том, что тело, непрерывное до деформации, остает- ся непрерывным и после приложения нагрузки. О д н о р о д н о с т ь тела гово- рит о том, что во всех точках тела под действием одинаковых сил возникают одинаковые деформации. И з о т р о п н о с т ь предполагает, что упругие свой- ства одинаковы по любому направлению, проведенному из данной точки тела. У п р у г о с т ь ю называется свойство тела восстанавливать свои первоначаль- ные размеры после снятия внешней нагрузки. Классические методы решения задач теории упругостиБыли получены уравнения равновесия сил, уравнения Коши, а также уравнения связи напряжений и деформаций, т.е. уравнения обобщенного закона Гука. Итого получено 15 уравнений, в которые входят 15 неизвестных (σx, σy, σz, τxy, τxz, τyz, εx, εy, εz, γxy, γxz, γyz, u, v, w). Таким образом, задача теории упругости может быть решена путем интегрирования этих уравнений при удовлетворении граничным условиям. Для этого могут быть использованы статические граничные условия или геометрические граничные условия, которые формулируются через перемещения. Существует два основных метода решения задач теории упругости: в перемещениях и в напряжениях. Решение задач теории упругости в перемещенияхПри решении задачи этим методом в качестве неизвестных принимаются компоненты вектора перемещений: u, v, w. С помощью уравнений обобщенного закона Гука напряжения выражаются через деформации, которые в свою очередь выражаются через перемещения с помощью уравнений Коши. Полученные зависимости напряжений от перемещений подставляются в уравнения равновесия. В результате получаются три уравнения равновесия в перемещениях, которые называются у р а в н е н и я м и Л а м е : ( λ+ G) ∂ ε + G 2 u + X =0; ∂ x (λ + G) ∂ ε + G 2 v+ Y=0; ∂ y (λ + G) ∂ε + G 2 w+ Z=0 , ∂ z (1.19) где λ =Eμ – коэффициент Ламе; (1+ μ)(1−2μ) ε=εx+ εy+ εz– относительная объемная деформация; 2= ∂2 ∂ x2 + ∂2 ∂ y2 + ∂2 ∂ z2 – оператор дифференцирования. Решения этих уравнений должны удовлетворять граничным условиям. Это могут быть геометрические граничные условия, которые накладываются непосредственно на перемещения, или статические граничные условия, которые по аналогии с уравнениями равновесия записываются через перемещения с помощью уравнений Коши, а также с помощью уравнений закона Гука. Далее по найденным из (1.19) перемещениям можно с помощью уравнений Коши определить деформации, а затем и напряжения с использованием закона Гука. Таким образом, задача теории упругости оказывается полностью решена. Решение задач теории упругости в напряженияхВ данном случае в качестве неизвестных принимаются компоненты вектора напряжений: σx, σy, σz, τxy, τxz, τyz. Уравнения совместности деформаций Сен-Венана выражаются с помощью закона Гука через напряжения. В результате преобразования с помощью уравнений равновесия сил они приводятся к следующему виду (при условии, что объемные силы отсутствуют): 2 ∂2σ 2 (1+ μ) σ x+ ∂ x2 =0 ; (1+ μ) 2 τ +∂ σ xy ∂ x∂ y =0 ; (1+ μ) 2 σ + ∂2 σ =0 ; y ∂ y2 (1+ μ) 2 τ + ∂2 σ =0 ; xz ∂ x∂ z (1.20) (1+ μ) 2 σ + ∂2 σ =0 ; z ∂ z2 (1+ μ) 2 τ + ∂2σ yz ∂ y∂ z =0 , где σ =σ x+ σ y+ σ z– объемное напряжение. Полученные зависимости называются у р а в н е н и я м и Б е л ь т р а м и – М и т ч е л а . Таким образом, при решении задачи в напряжениях необходимо интегрировать девять уравнений: три уравнения равновесия сил и шесть полученных уравнений совместности деформаций (1.20). Далее по полученным напряжениям с помощью закона Гука определяются деформации, а затем из уравнений Коши находятся перемещения. Полученное решение должно удовлетворять граничным условиям (геометрическим или статическим). 3. Основы вариационного исчисления Вариационное исчисление является одной из старейших математических дисциплин. Оно развивалось почти одновременно с математическим анализом. Обычно основателями вариационного исчисления считают братьев Бернулли, Эйлера, Лагранжа. Вариационное исчисление примыкает к теории максимумов и минимумов математического анализа и является основой методов оптимального проектирования. В вариационном исчислении исследуются функционалы - объекты, более сложные, чем функции. Вариационное исчисление тесно связано с приложениями математики к механике, физике, инженерному делу, технике, численному анализу. Приведем несколько примеров, которые дают представление о целях и задачах вариационного исчисления. 1. Задача о брахистохроне. Задача была сформулирована в 1696 году Иоганом Бернулли: отыскать кривую, двигаясь по которой под действием только силы тяжести (без трения) материальная точка попадет из точки A в точку B, находящихся в разных уровнях, в кратчайшее время (рис. 1.1).  На основании закона движения твердого тела массой т под действием сила тяжести имеем: На основании закона движения твердого тела массой т под действием сила тяжести имеем: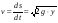 - скорость дви-жения точки; у - расстояние по вертикали; s(x,y) - длина дуги кривой движения точки; - скорость дви-жения точки; у - расстояние по вертикали; s(x,y) - длина дуги кривой движения точки; ; ; 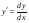 ; g - ускорение силы тяжести. ; g - ускорение силы тяжести.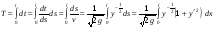 . (1.1) . (1.1) Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, И. Ньютоном, Г. Лопиталем. Оказалось, что линией быстрейшего ската является циклоида. 2. Задача о геодезических кривых. Требуется определить линию наименьшей длины, соединяющую две точки. Решение этой задачи в обычном трехмерном пространстве известно - кратчайшим расстоянием, соединяющим две точки, является прямая линия. Однако задача осложняется, если рассматривать точки какой либо поверхности. Эта задача рассматривается в курсе дифференциальной геометрии. Линии кратчайшего расстояния, соединяющие точки поверхности, называются геодезическими кривыми. Эта задача имеет важное прикладное значение в геодезии. Если рассматривать точки сферы, то линия кратчайшего расстояния между двумя точками является дугой окружности в плоскости, проходящей через заданные точки и центр сферы. Если рассматривать точки цилиндрической или конической поверхностей, то ответ о линии кратчайшего пути между двумя точками уже не является столь простым и очевидным. 3. Задача о минимальных поверхностях. Минимальной поверхно стью называют поверхность минимальной площади, натянутую на заданный контур. Сформулируем задачу о минимальной поверхности вращения (рис. 1.2). Площадь поверхности вращения определяется формулой 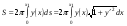 . (1.2) . (1.2) На практике минимальная поверхность может быть получена с помощью мыльной пленки, натянутой на за-данный контур. Минимальные поверхности могут использоваться для оптимального проектирования пространственных оболочечных конструкций. 4. Задача о наибольшей площади. Определить замкнутую кривую заданной длины, ограничивающую наибольшую площадь. Решением данной задачи является окружность. Однако, задача осложнится, если часть кривой, ограничивающей искомую площадь является заданной незамкнутой кривой, к которой необходимо добавить искомую незамкнутую кривую заданной длины, сопряженную с заданной кривой. Приведенные примеры позволяют получить представления о задачах, которыми занимается вариационное исчисление - из множества функций найти функцию - кривая движения тела, линия на поверхности, образующая поверхности вращения, площадь, ограничиваемая кривой линией, для которой достигается минимум (максимум) некоторого параметра - время движения, длина кривой, площадь поверхности или площадь внутри контура заданной длины. 4. Вариационные методы решения задач теории упругостиЗадачи теории упругости могут быть решены с помощью энергетических методов, которые позволяют избежать математических затруднений, связанных с интегрированием дифференциальных уравнений. Данные методы опираются на раздел высшей математики, который называется в а р и а ц и о н н ы м и с - ч и с л е н и е м , поэтому их называют вариационными методами. В вариационном исчислении используется понятие ф у н к ц и о н а л а – переменной величины, зависящей от некоторого множества функций. Можно сказать, что функционал – это функция от функций. Чаще всего вариационное исчисление используется для отыскания функции, на которой данный функцио- нал достигает экстремального (наибольшего или наименьшего) значения. 4.1 Вариационный метод решения задач в перемещенияхВ вариационных методах теории упругости используются понятия воз- можного перемещения и возможной работы. В о з м о ж н о е ( в и р т у а л ь - н о е ) п е р е м е щ е н и е точки, принадлежащей некоторой механической си- стеме, – это такое элементарное (бесконечно малое) перемещение, которое точ- ка может совершать из занимаемого в данный момент времени положения, не нарушая наложенных на нее связей. Возможных перемещений точки может быть бесконечно много, а в действительности реализуется какое-то одно. Д е й - с т в и т е л ь н ы м п е р е м е щ е н и е м точки называют такое элементарное перемещение, которое она фактически совершает за некоторый бесконечно ма- лый промежуток времени при данных связях. Действительное элементарное перемещение обозначается с помощью зна- ка д и ф ф е р е н ц и а л а d, например, dr. Возможное перемещение, чтобы от- личать его от действительного, обозначается с помощью знака в а р и а ц и и δ, например, δ r. Для оператора δ в вариационном исчислении приняты такие же математические правила, как и для оператора d в дифференциальном исчисле- нии. По аналогии с оператором d, называемым первым дифференциалом, опе- ратор δ называется первой вариацией. Соответственно d 2 – второй дифферен- циал, а δ2 – вторая вариация и т.д. В о з м о ж н а я ( в и р т у а л ь н а я ) р а б о т а – это элементарная рабо- та силы P, приложенной к точке, на возможном перемещении δ r: δ Э=Pδ rcos α= Prδ r, (1.27) где α – угол между силой Pи возможным перемещением δ r; Pr – проекция силы P на направление возможного перемещения δ r. Существует п р и н ц и п в о з м о ж н ы х п е р е м е щ е н и й , который гласит: для равновесия материальной точки, находящейся под действием актив- ных сил и подчиненной идеальным связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил равнялась нулю на любом воз- можном перемещении точки: ∑ δ Эi=∑ Priδ r=0. (1.28) i i Данное выражение справедливо, в частности, при условии, что сумма проекций активных сил на любое направление равна нулю: ∑ Pri=0. (1.29) i Полная Энергия упругой системы Упругое тело можно рассматривать как систему материальных точек. Если упругое тело находится в покое под действием поверхностных объёмных сил, то это значит, что на каждую его точку действуют уравновешенные силы. Если произошло возможное перемещение каждой из точек тела, то для выполнения условия равновесия тела общая возможная работа, произведенная всеми силами, должна быть равна нулю. Выражение для потенциальной энергии деформации U, соответствующей работе внутренних сил, было получено выше. Найдем теперь выражение для работы внешних сил A, т.е. объемных и поверхностных сил. При возможных перемещениях δu, δv, δw суммарная работа объемных и поверхностных сил равна: δ A=∭( Xδ u+ Yδ v+ Zδ w) dxdydz+ ∬( Xnδ u+ Ynδ v+ Znδ w) dS. (1.30) Когда система получает возможное перемещение, внешние силы счита- ются постоянными, поэтому оператор δ можно вынести за знаки интегралов: δ A=δ [∭( Xu+ Yv+ Zw) dxdydz+ ∬( Xnu+ Ynv+ Znw) dS]. (1.31) Тогда выражение для работы внешних сил будет иметь вид: A=∭( Xu+ Yv+ Zw) dxdydz+ ∬( Xnu+ Ynv+ Znw) dS. (1.32) Выше было отмечено, что работа всех активных сил δЭ, произведенная на возможном перемещении, обращается в нуль. Поэтому: δ Э=δ U−δ A=δ(U− A)=0. (1.33) Откуда: Э=U− A. (1.34) Величина Э называется п о л н о й э н е р г и е й у п р у г о й с и с т е - м ы . Вариационный принцип ЛагранжаВариаци о н н ы й п р и н ц и п Л а г р а н ж а может быть сформули- рован следующим образом: в упругой системе, находящейся под действием внешних сил, из всех кинематически возможных сочетаний перемещений u, v, w в действительности реализуются лишь те, которые сообщают минимум пол- ной энергии системы. Под кинематически возможными здесь понимаются перемещения, кото- рые удовлетворяют геометрическим граничным условиям на поверхности тела и связаны с относительными деформациями соотношениями Коши. Таким образом, полная энергия упругого тела, в котором имеет место быть действительное поле перемещений, должна быть минимальной. Посколь- ку полная энергия Э выражается через интегралы (1.24) и (1.32), она является функционалом. Согласно вариационному исчислению реализация принципа Ла- гранжа сводится, таким образом, к задаче минимизации функционала. Если уравнения закона Гука (1.18) выразить в форме, разрешенной отно- сительно напряжений: σ x=2 Gεx+ λ ε ; σ y=2 Gεy+ λ ε ; σ z=2 Gεz+ λ ε ; τ xy=Gγxy; τxz=Gγxz; τ yz=Gγyz, (1.35) + ∂ z + 2 ∂ x+ ∂ y+ ∂ z + а затем полученные выражения подставить в формулу для потенциальной энер- гии деформации (1.24), функции деформации выразить через перемещения с помощью соотношений Коши (1.14) и (1.16), а работу внешних сил взять в виде (1.32), то полную энергию упругой системы можно записать следующим об- разом: Э=∭ G ∂ x + ∂ y [(∂ u)2 (∂ v)2 (∂w)2] λ (∂ u ∂ v∂w)2 + 2 ∂ y+ ∂ x dxdydz− G[(∂ u ∂ v)2 (∂ u ∂w)2 (∂ v ∂ w)2] (1.36) + ∂ z+ ∂ x + ∂ z+ ∂ y −∭( X u+Y v+Z w) dxdydz −∬( X n u+Y n v + Zn w) dS. Минимизируя данный функционал, можно получить три уравнения отно- сительно функций перемещений u, v, w и граничные условия, совпадающие со статическими граничными условиями (1.10), которые записываются через пере- мещения. Таким образом, вариационный принцип Лагранжа является аналогом метода решения задачи теории упругости в перемещениях. 4.2 Вариационный метод решения задач в напряженияхДля решения задач теории упругости вариационными методами можно рассматривать не вариации перемещений, а вариации напряжений. При этом необходимо помнить, что в этом случае требуется удовлетворение не только уравнениям равновесия и граничным условиям на поверхности тела, но и урав- нениям совместности деформаций. Дополнительная потенциальная энергия деформацииВведем понятие дополнительной потенциальной энергии деформации. По аналогии с (1.26) выражение для ее определения запишем в виде: U=∭Wdxdydz. (1.37) Вариацию удельной дополнительной потенциальной энергии деформации свяжем с вариациями напряжений, основываясь на выражении (1.25): δ W=εxδ σ x+ εyδ σ y+ εzδ σ z+ γxyδ τ xy+ γxzδ τ xz+ γyzδ τ yz. (1.38) Используя формулы закона Гука (1.18) и интегрируя, получим: W=1 (σ2+ σ2+ σ2)− μ (σ σ + σ σ + σ σ )+1 ( τ2 + τ2 + τ2 ). (1.39)
y z E x y x z y z 2 G xy xz yz Чтобы показать соотношение удельной потенциальной энергией W с удельной дополнительной потенциальной энергией W , рассмотрим одноосное растяжение стержня вдоль оси x. В этом случае все компоненты напряжений, кроме σx, обращаются в нуль. Поэтому для удельной потенциальной энергии имеем: δ W=σ xδ εx, (1.40) а для удельной дополнительной потенциальной энергии имеем: δ W=εxδ σ x. (1.41) Учитывая соотношение закона Гука для рассматриваемого случая σ x= E εx, получим: εx ε x Eε2 σ ε W=∫σ δ ε = E∫ε δ ε =x=xx, (1.42) x 0 σ x x x x 0 1 σ x 2 2 σ2 σ ε W =∫ε δ σ = ∫σ δ σ =x=xx. (1.43) E x x x 0 0 x 2 E 2 Таким образом, для линейно-упругого тела W =W . Из геометрического смысла интеграла (площадь под кривой) следует, что интегралы (1.42) и (1.43) представляют собой площади треугольников, показан- ных на рис. 1.7а. Для нелинейно-упругого тела W ≠W (рис. 1.7б). W W εx W W εx σ x σ x O а) для линейно-упругого тела O б) для нелинейно-упругого тела Рис. 1.7. Соотношение удельной потенциальной энергии и удельной дополни- тельной потенциальной энергии деформации при одноосном растяжении Вариационный принцип КастильяноЗапишем по аналогии с (1.34) выражение для п о л н о й д о п о л н и - т е л ь н о й э н е р г и и у п р у г о й с и с т е м ы : Э=U− A. (1.44) В а р и а ц и о н н ы й п р и н ц и п К а с т и л ь я н о является законом, позволяющим строить решение задачи в напряжениях. Он может быть сформу- лирован следующим образом: из всех статически возможных систем напряже- ний в действительности в упругой системе возникают лишь те, которые сооб- щают стационарное (в данном случае минимальное) значение полной дополни- тельной энергии. Напомним, что у функций могут быть точки, которые называются стацио- нарными (особыми, критическими). Это точки, в которых дифференциал функ- ции обращается в нуль, что является необходимым (но не достаточным) усло- вием экстремума (минимума или максимума). Значение функции в данной точ- ке называют стационарным (или критическим). Функционалы по аналогии с функциями тоже могут иметь стационарные значения, которые им сообщают их аргументы-функции. Поскольку полная дополнительная энергия есть функционал, то условием его стационарности является обращение в нуль первой вариации: δ Э=0. (1.45) Статически возможными называются системы напряжений, удовлетворя- ющие уравнениям равновесия (1.3) и граничным условиям на поверхности (1.10). Для решения задачи в напряжениях необходимо также удовлетворить уравнениям совместности деформаций (1.17). Из выражений (1.44) и (1.45) вытекает: δ Э=δ U−δ A=0. (1.46) Раскроем вариацию дополнительной потенциальной энергии деформации с учетом (1.37) и (1.38), а вариацию работы внешних сил запишем по аналогии с (1.30) через вариации этих сил. Учтем при этом, что объемные силы X, Y, Z яв- ляются заданными и, следовательно, их вариации равны нулю: δ Э=∭(εxδ σ x+εyδ σ y+εzδ σ z+ γxyδ τ xy+ γxzδ τ xz+γ yzδ τ yz) dxdydz− −∬( u δ X n +v δ Y n+ w δ Z n) dS =0. (1.47) Принцип наименьшей работыНа практике обычно рассматривается случай, когда нагрузки на поверх- ности тела Xn, Yn, Znзаданы. Тогда их вариации равны нулю: δ Xn=δ Yn=δ Zn=0 . В этом случае вариация работы внешних сил, как это следует из уравне- ния (1.47), также будет равна нулю: δ A=0. Тогда из формулы (1.46) вытекает: δ U=0. (1.48) Это и есть п р и н ц и п н а и м е н ь ш е й р а б о т ы , который иногда на- зывают п р и н ц и п о м м и н и м у м а д о п о л н и т е л ь н о й п о т е н ц и - а л ь н о й э н е р г и и , он формулируется следующим образом: из всех стати- чески возможных систем напряжений, сводящихся на поверхности тела к задан- ным нагрузкам, в действительности в упругой системе возникают лишь те, ко- торые сообщают минимальное значение дополнительной потенциальной энер- гии. σ + σ σ + σ σ )+ 1 ( τ2 + τ2 + τ2 ) dxdydz.(1.49) Для реализации данного принципа необходимо минимизировать функци- онал, который получается при подстановке (1.39) в (1.37): U=∭ 1 (σ2 + σ2 + σ2 )− μ (σ [2 Ex y z E x y x z y z 2 G xy xz yz] Входящие в формулу (1.49) функции напряжений должны удовлетворять уравнениям равновесия (1.3) и статическим граничным условиям (1.10). Мини- мизация данного функционала приводит к системе уравнений, которые являют- ся уравнениями совместности деформаций, записанными через напряжения. Теорема КастильяноПусть имеется упругая система, напряженное состояние которой опреде- лено. Требуется найти перемещение r некоторой точки этой системы по направ- лению, заданному направляющими косинусами: cos(̂x , r)=k, cos(̂y, r)=l, cos(̂z, r)=m. Приложим в данной точке неизвестную силу Pr, сов- падающую по направлению с искомым перемещением. Проекции силы Pr на оси системы координат, связанной с рассматриваемой системой, будут равны: Prx= Prk; Pry= Prl; Prz= Prm. (1.50) Работа сил на перемещениях u, v, w будет равна: A= Prku+ Prlv+ Prmw= Pr( ku+ lv+ mw). (1.51) Записанная в скобках величина является искомым перемещением: r=ku+ lv+ mw. (1.52) Тогда работу можно записать в виде: A= Prr, (1.53) r= ∂ U. (1.54) ∂ P r Полученное выражение формулируется в виде т е о р е м ы К а с т и л ь я - н о : частная производная от дополнительной потенциальной энергии по сило- вому фактору равна перемещению по направлению этого силового фактора. В качестве силового фактора может рассматриваться сила или момент. Если в качестве Pr берется момент, то r будет углом поворота. 5. Литература
/ пер. с нем. – М.: Наука, 1980. – 976 с.
Феодосьев В.И. Сопротивление материалов: учебник для втузов – изд. 9-е, перераб. – М.: Наука. Гл. ред. физ.-мат. лит., 1986. – 512 с | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
