Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда. Второй закон Ньютона. Движение под действием постоянной силы. Минобрнауки россии
 Скачать 0.55 Mb.
|
|
Вывод формулы для центростремительного ускорения По определению . 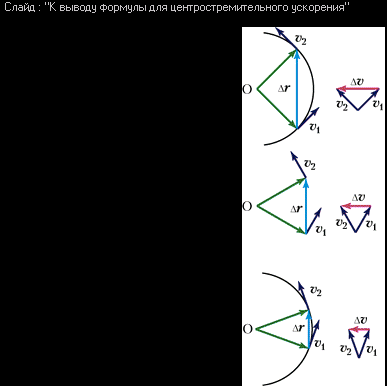 (19) Рисунок 6 Вывод формулы центростремительного ускорения На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что  =  = R и  =  = υ, из подобия треугольников находим: (20)откуда  (21)Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом φ, измеряемым в радианах (рад), причем x = R cos(φ + φ0), y = R sin(φ + φ0), (22) где φ0 определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени). В случае равномерного вращения угол φ, измеряемый в радианах, линейно растет со временем: φ = ωt, (23) где ω называется циклической (круговой) частотой. Размерность циклической частоты: [ω] = c–1 = Гц. Циклическая частота равна величине угла поворота (измеренного в рад) за единицу времени, так что иначе ее называют угловой скоростью. Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде: x 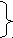 = R cos(ωt + φ0), (24)y = R sin(ωt + φ0). Время, за которое совершается один оборот, называется периодом T. Частота ν = 1/T. (25) Размерность частоты: [ν] = с–1 = Гц. Связь циклической частоты с периодом и частотой: 2π = ωT, откуда ω = 2π/T = 2πν. (26) Связь линейной скорости и угловой скорости находится из равенства: 2πR = υT, откуда υ = 2πR/T = ωR. (27) Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом: aц = υ2/R = ω2R = 4π2ν2R = 4π2R/T2. (28) 4.6 Связь поступательного и вращательного движений Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость υ и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение φ, угловая скорость ω и угловое ускорение ε (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками: перемещение s → угловое перемещение φ = s/R; скорость υ → угловая скорость ω = υ /R; ускорение a → угловое ускорение ε = a/R. Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например: s = υt → φ = ωt, (29) υ = υ0 + at → ω = ω0 + εt. (29а) Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор  , проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела  , направленному по касательной к окружности в этой точке. Определим вектор  , который по модулю равен угловой скорости ω и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора . Тогда связь трех взаимно перпендикулярных векторов , и можно записать с помощью векторного произведения векторов: . (30)4.7 Динамика. Законы Ньютона. Принцип относительности Галилея Динамика – раздел механики, изучающий законы взаимодействия тел. В природе известны четыре фундаментальных взаимодействия: гравитационное, электромагнитное, сильное и слабое. Проявления первых двух взаимодействий наблюдаются непосредственно органами чувств человека, в то время как сильные и слабые взаимодействия управляют процессами, происходящими в глубинах ядер атомов, и прямому наблюдению недоступны. Гравитационное взаимодействие (ГВ) присуще всем без исключения материальным объектам во Вселенной и проявляется в притяжении тел друг к другу. ГВ действует на больших расстояниях.  Рисунок 7 Движение Земли вокруг Солнца обусловлено гравитационным взаимодействием Электромагнитное взаимодействие (ЭМВ) определяет структуру атомов и молекул всех веществ. Поэтому опосредованным образом именно электромагнитное взаимодействие определяет свойства и поведение всех окружающих нас тел.  Рисунок 8 Структура атомов определяется электромагнитным взаимодействием Фундаментальные взаимодействия между телами порождают силы взаимодействия – силу тяжести, магнитную силу, действующую на провод с током, силу трения, выталкивающую силу и т.д. Таким образом, сила есть количественная характеристика взаимодействия между телами. В реальной жизни человек непосредственно сталкивается с силами, порождаемыми мускульными усилиями и действием разного рода механизмов, с силами трения между телами, упругими силами и т.п. Из опыта можно установить следующие общие свойства сил:
Сила заставляет тело либо деформироваться, либо двигаться с ускорением. Основополагающие законы классической механики были установлены английским физиком И. Ньютоном. 4.8 Первый закон Ньютона Если сумма всех сил, действующих на тело, равна нулю, то существует такая система отсчета, относительно которой поступательно движущееся тело сохраняет свою скорость неизменной. Такая система отсчета называется инерциальной системой отсчета (ИСО). Иногда первый закон Ньютона называют законом инерции, а равномерное движение тела относительно ИСО называют движением по инерции. С высокой степенью точностью инерциальной можно считать гелиоцентрическую (звездную) систему отсчета (начало координат находиться в центре Солнца, а оси проведены в направлении определённых звёзд). Система отсчёта, связанная с Землёй, строго говоря, неинерциальна, однако эффекты, обусловленные её неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца) пренебрежимо малы, поэтому при решении многих задач её можно считать инерциальной. Инерциальной системой отсчёта является такая, которая либо покоится, либо движется равномерно и прямолинейно относительно како-то другой инерциальной системы. Любая система отсчета, движущаяся относительно ИСО равномерно и прямолинейно, также является инерциальной. Таким образом, существует бесконечно много ИСО, которые движутся относительно друг друга с неизменными по величине и направлению скоростями. 4.9 Понятие массы Масса тела m является количественной характеристикой инертности тела, т.е. его способности изменять скорость, (получать ускорение или ускоряться) под действием заданных сил. Метод измерения массы – взвешивание на рычажных весах (сравнение с эталоном). Единицей измерения массы в СИ является килограмм (кг). 4.10 Второй закон Ньютона В ИСО ускорение тела пропорционально полной силе, действующей на тело, и обратно пропорционально массе тела: 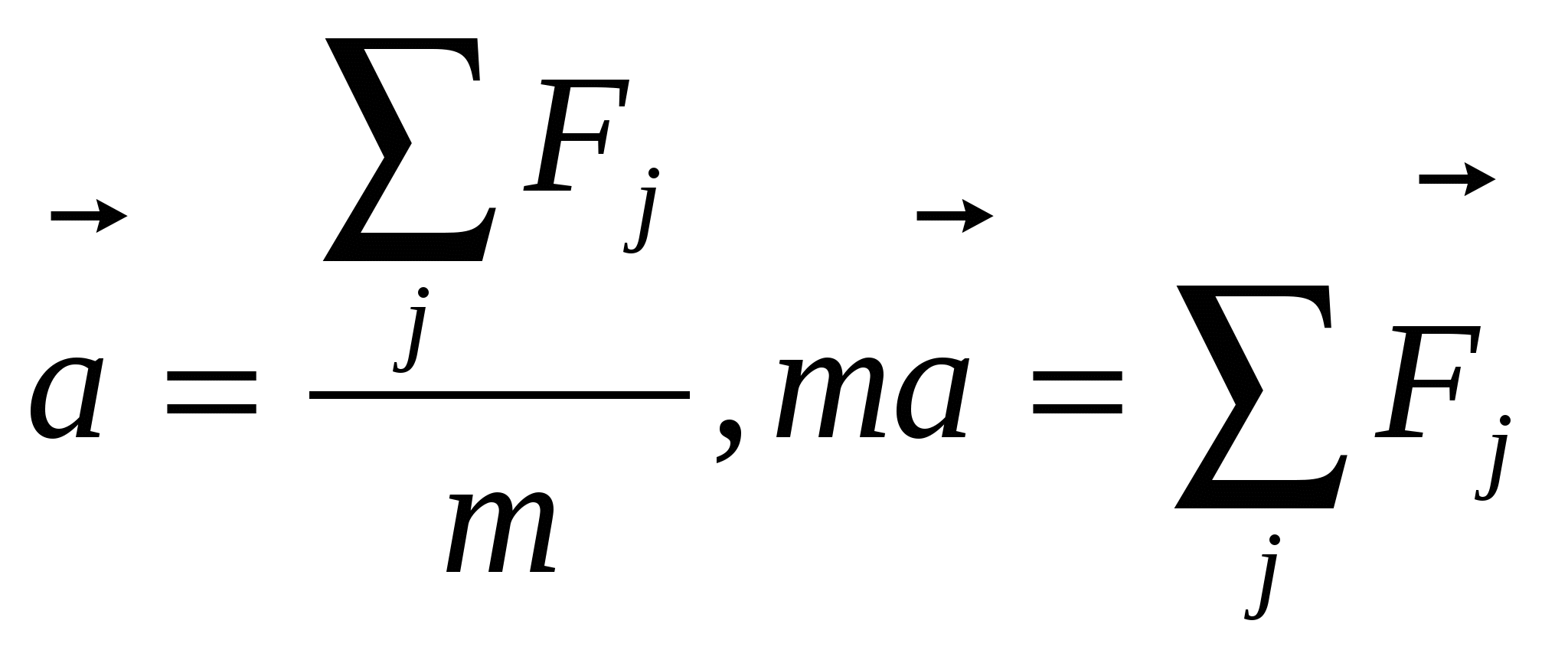 (31)Учитывая, что  , можно записать второй закон Ньютона в дифференциальной форме: (32)Иначе этот же закон можно записать в виде:  (33)Следует подчеркнуть, что смысл второго закона Ньютона заключается в том, что он определяет динамический принцип классической физики: ускорение тела определяется действующими на него силами, которые, в свою очередь, определяются экспериментально. Единицей измерения силы является ньютон (Н), так что размерность силы [F] = [Н]. 4.11 Третий закон Ньютона Для любой пары взаимодействующих тел сила  12, действующая со стороны первого тела на второе, равна по величине и противоположна по направлению силе 21, действующей со стороны второго тела на первое. Следует помнить, что эти силы приложены к разным телам!4.12 Принцип относительности Галилея Преобразования Галилея (см. Кинематика равномерного поступательного движения) определяют, как преобразуются координаты и время события при переходе от одной ИСО к другой. Опыт показывает, что механические явления протекают одинаково, независимо от того, с какой постоянной скоростью движется лаборатория. Этот фундаментальный закон природы носит название принципа относительности Галилея и может быть сформулирован следующим образом. Все законы классической механики не меняют своего вида при переходе от одной ИСО к другой, т.е. законы механики инвариантны (не меняют своего вида) относительно преобразований Галилея. 4.13 Определение ускорения свободного падения с помощью машины Атвуда Ускорение свободного падения g можно найти с помощью простого опыта: бросить тело с известной высоты h и измерить время падения t, а затем из формулы h = gt2/2 вычислить g. В действительности дело обстоит не так просто, если требуется определить g достаточно точно. Определим время t падения с высоты h =1,0 м при g, равном 9.8 м/с2:  ,  (34)По нашей оценке при проведении такого эксперимента необходимо измерять время с точностью до 0,01 с. Оценим разброс для t1= 0,44 с; t2 = 0,45 с; t3 = 0,46 с по формуле g = 2h/t2: g1=  =10,3300578м/с2≈10,3 м/с2g2=  =9,8765431м/с2≈9,9м/с2g3=  =9,4517956м/с2≈9,4м/с2Понятно, что измерить время с точностью до 0,01 с не просто. Наручные часы или спортивный секундомер для такой цели непригодны. Если увеличить высоту, то время падения тоже увеличится. Так при h= 5 м время падения будет 1 с, а при h = 20 м — 2 с. В этом случае можно ограничиться меньшей точностью при измерении времени, например 0,1 с, но возникает ошибка другого характера. Сопротивление воздуха при больших скоростях играет заметную роль. Формула h = gt2/2 описывает равноускоренное движение и, конечно, не учитывает сопротивления воздуха. Таким образом, увеличивая высоту h, мы увеличиваем время падения и уменьшаем относительную погрешность измерения времени, но при этом вносим другую ошибку: сама формула h = gt2/2 становится неточной. Более того, если кирпич сбросить с высоты h≈ 500 м, то примерно первые 200 м он будет двигаться с ускорением, а затем сила сопротивления воздуха станет равной силе тяжести (это будет при скорости примерно 70 м/с) и тело остальные 300 м будет падать с постоянной скоростью ≈ 70 м/с. В этом случае формула h = gt2/2 становится неверной. Этот простой пример наглядно подчеркивает общую черту любого физического эксперимента. В любом эксперименте точность измерений какой-либо физической величины связана не только с точностью измерительных приборов, но и с тем, насколько точно принятая модель описывает данный опыт. В рассматриваемом нами опыте мы видим, что точность измерения ускорения g связана не только с точностью измерения времени t, но и с тем можно или нет пренебречь трением о воздух. Иными словами; достаточно точно или нет описывает формула h = gt2/2 движение тела. Трудности опыта связаны с большим значением ускорения свободного падения. Так как ускорение большое, то тело быстро набирает скорость, а при этом или время падения мало и его трудно точно измерить, или сама формула h = gt2/2 не точна. Уменьшить ускорение можно с помощью устройства, которое называют машиной Атвуда (рисунок 10). 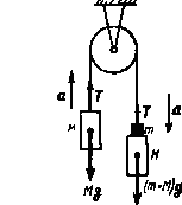 Рисунок 10 Принципиальная схема установки Через блок перекинута нить, на которой закреплены грузы массой М каждый. На один грузов кладется перегрузок массой т. Ускорение грузов легко найти, если ввести два предположения (выбрать модель!): 1) блок и нить невесомы, т. е. их массы равны нулю; 2) трением тела о воздух и трением между блоком и его осью можно пренебречь. С учетом этих предположений уравнения движения грузов имеют вид
где Т — сила натяжения нитей, а — ускорение грузов. Из уравнений (1) получаем  (36)где ε = m/(2М). Время, за которое груз опускается на высоту h, равно  (37)Формально из выражения (37) следует, что время падения груза может быть сколь угодно большим, если уменьшить ε. Например, если взять грузы массами М = 5 кг каждый, перегрузок массой т = 1 г, то ε = 10-4, а время спуска груза на высоту h = 1 м примерно равно 45 с. Это время можно достаточно точно измерить секундомером. Однако реально такой опыт невыполним. Мы предположили, что трение в оси блока отсутствует. Но в действительности оно есть. Весь вопрос в том, можно ли им пренебречь или нет. Если подвесить к блоку на нитях тяжелые грузы, то в оси блока будет большая сила трения. Чем массивнее грузы, тем больше силатрения. Значит, необходимо брать достаточно тяжелый перегрузок, чтобы преодолеть эту силу трения и привести всю систему в движение. Сделаем теперь количественные оценки. Пусть m0 — масса такого перегрузка, который только-только страгивает блок с грузами. Это значит, что любой перегрузок меньшей массы не приводит систему в движение. В этом случае момент сил натяжения нитей равен моменту силы трения Мтр в оси блока:  (38)где T2= (M + m0) g и T1 = Mg — силы натяжения нитей, R — радиус блока (рисунок 11). Момент силы трения в оси блока 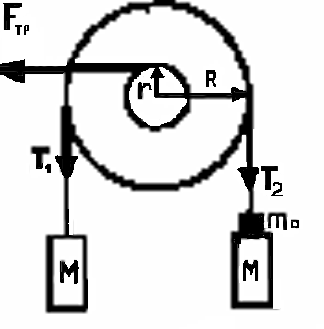 |