Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда. Второй закон Ньютона. Движение под действием постоянной силы. Минобрнауки россии

• Название: Минобрнауки россии
• Анкор: Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда.doc
• Дата: 02.02.2017
• Размер: 0.55 Mb.
• Имя файла: Второй закон Ньютона. Движение под действием постоянной силы. Ма.doc
• Тип: Методические указания; #1757
• страница: 1 из 3

МИНОБРНАУКИ РОССИИ

Егорьевский технологический институт (филиал)

федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Московский государственный технологический университет «СТАНКИН»

(ЕТИ ФГБОУ ВПО МГТУ «СТАНКИН»)

Факультет технологии и управления производствами

Кафедра естественнонаучных дисциплин


Второй закон Ньютона. Движение под действием

постоянной силы. Машина Атвуда

Методические указания к выполнению лабораторной работы

ЕТИ. Ф.ЛР.02.

г. Егорьевск 2014
Составители: _____________ В.Ю. Никифоров, ст. преподаватель ЕНД

В методических указаниях рассмотрены основные понятия механики, кинематики и динамики поступательного и вращательного движений, изучение динамики поступательного движения связанной системы тел с учетом силы трения; определение ускорения свободного падения с помощью машины Атвуда, оценка роли трения как источника систематической погрешности при определении ускорения свободного падения на лабораторной установке.

Методические указания предназначены для студентов 1 курса, обучающихся по направлениям подготовки бакалавров: 151900 Конструкторско-технологическое обеспечение автоматизированных машиностроительных производств, 220700 Автоматизация технологических процессов и производств, 280700 Техносферная безопасность для лабораторных работ по дисциплине "Физика.
Методические указания обсуждены и одобрены на заседании учебно-методической группы (УМГ) кафедры ЕНД

(протокол № ___________ от __________г.)

Председатель УМГ _____________ Г.Г Шабаева
Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда

1. 
   Цель работы: изучение динамики поступательного движения связанной системы тел с учетом силы трения; оценка роли трения как источника систематической погрешности при определении ускорения свободного падения на лабораторной установке.
   
2. 
   Оборудование: установка «машина Атвуда», набор грузов, электронный секундомер
   

3. 
   Содержание работы
   

3.1 Изучить теоретический материал.

3.2 Определите массу m₀ страгивающего перегрузка

3.3 Определите экспериментально зависимость времени падения t груза от высоты h.

3.4 Определите опытным путём зависимость времени падения t от массы m перегрузка.

3.5 По результатам измерений зависимости времени падения t груза от высоты h построить в осях координат х = , у = t прямую t= t(). По наклону прямой определите а.

3.6 По результатам измерений зависимости времени падения t от массы m перегрузка в осях координат х =, у= t постройте прямую t = t ()

3.7 По наклону прямой с помощью соотношения (44) определите ускорение свободного падения g и погрешность Dg.

3.8 Сделать вывод. Записать полученный результат в виде g= ±Δg.

3.9 Оформить отчет.

4. 
   Теоретические сведения к работе
   

4.1 Основные понятия механики

Изменение положения тела в пространстве по отношению к другим телам с течением времени называется механическим движением. Раздел физики, изучающий механическое движение, называется механикой. Раздел механики, изучающий движение тел независимо от причин, вызвавших это движение, называется кинематикой.

При движении в пространстве точки тела описывают траектории.

Простейшими видами механического движения являются поступательное движение (такое движение, при котором прямая, проведенная через любые две точки тела, перемещается параллельно самой себе) и вращательное движение (все точки тела описывают концентрические окружности вокруг общей оси).

Во многих случаях движущееся тело можно рассматривать как материальную точку (если размеры тела малы по сравнению с расстояниями до других тел и его ориентация несущественна). Если это не оговорено особо, во всех задачах механики, рассматриваемых ниже, это условие выполняется, так что можно говорить о движении материальных точек. Например, расстояние от Земли до Солнца (1,5·10⁸ км) много больше размеров как Земли (6,4·10³ км), так и Солнца (7·10⁵ км), поэтому с хорошей точностью можно рассматривать движение этих (и всех других) тел Солнечной системы как движение материальных точек. При изучении полета теннисного мяча можно во многих случаях пренебречь его размерами.

Движение тела в пространстве математически описывается в произвольно выбранной системе отсчета. Система отсчета состоит из:

1. Тела отсчета О.

2. Системы координат (в данном случае декартовой).

3. Часов, синхронно идущих во всех точках пространства.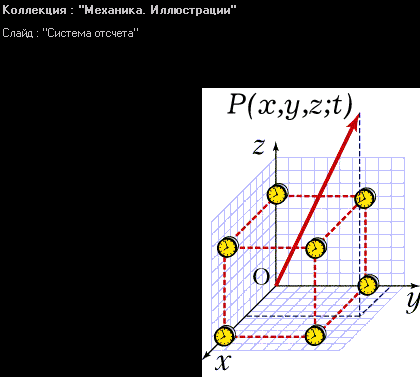



Рисунок 1 Система отсчёта
С точки зрения наблюдателей в разных системах отсчета одно и то же движение может выглядеть совершенно по-разному. Механическое движение относительно.

Положение материальной точки в пространстве в заданный момент времени определяется радиусом-вектором этой точки (t). В декартовой системе координат

;

(1)

Задание декартовых координат x(t), y(t) и z(t) как функций времени определяет закон движения материальной точки. Частными случаями движения являются движение в заданной плоскости (для его описания достаточно двух координат x(t) и y(t)) и движение вдоль заданной прямой (ее всегда можно выбрать за ось x декартовой системы).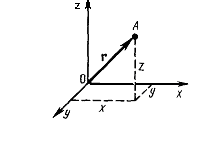



Рисунок 2 Радиус-вектор к заданной точке

При движении материальной точки конец радиуса-вектора, проведенного в эту точку, описывает траекторию. Каждая точка траектории соответствует значениям координат x, y, z в данный момент времени. Например, при движении на плоскости траектория может быть задана как кривая, описываемая функцией y(x). Длина траектории между начальной и конечной точками называется путем, а вектор, соединяющий начальную и конечную точки траектории, называется перемещением. Если начальная и конечная точки заданы радиусами-векторами 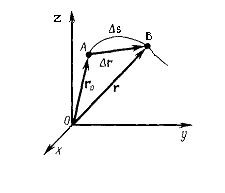и , то перемещение = – .



Рисунок 3 Траектория, путь, перемещение точки

Напомним, что векторы складываются одним из двух эквивалентных способов:

а) начала двух векторов совмещаются, и на этих векторах строится параллелограмм, диагональ которого равна сумме векторов (правило параллелограмма);

б) начало второго вектора совмещается путем параллельного переноса с концом первого вектора, и проводится вектор, соединяющий начало первого и конец второго векторов.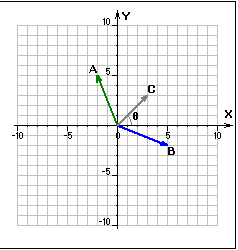


Рисунок 4 Траектория, путь, перемещение точки

Если точка последовательно совершает несколько перемещений, то полное перемещение равно векторной сумме отдельных перемещений:



Следует обратить внимание на то, что величина перемещения s = ||, вообще говоря, не совпадает с путем (например, вернувшись в ту точку, откуда начато движение, тело проходит отличный от нуля путь, но перемещение равно нулю). В случае одномерного движения проекция перемещения s_х=x – x₀ может быть как положительной, так и отрицательной.

Единицами измерения пройденного пути и времени в СИ являются метр (м) и секунда (с). Размерность какой-то физической величины обозначается символом этой величины в квадратных скобках. Таким образом, [l] = = м, [t] = с.
4.2 Кинематика равномерного поступательного движения

Средняя скорость движения материальной точки за интервал времени Δt = t₂ – t₁ определяется как

(2)

Здесь = перемещение тела за время Δt.

Размерность скорости: [υ] = м/с.

Если движение таково, что средняя скорость за любой промежуток времени не меняется ни по величине, ни по направлению, то такое движение называется равномерным прямолинейным движением. В этом случае

, (3)

где = const и отсчет времени начат от момента t₁ = 0, так что можно принять Δt = t. В случае равномерного прямолинейного движения путь совпадает с модулем перемещения.

Формула для перемещения при равномерном движении есть первый пример математической записи определенного физического закона. Этот закон имеет вид равенства одного вектора () другому вектору (t). Следует всегда помнить, что это сокращенная форма записи трех равенств:

s_x = υ_xt, s_y = υ_yt, s_z = υ_zt

в произвольно выбранной декартовой системе координат. Другой тип математической записи физических законов, встречающийся в школьном курсе физики, – равенство одного числа (или скаляра) другому числу: А = В.

Уравнения прямолинейного равномерного движения принимают наиболее простой вид в системе координат, одна из осей которой (например, ось x) направлена вдоль вектора скорости . Тогда компоненты скорости будут: υ_x = υ, υ_y = 0, υ_z =0.

Уравнения прямолинейного равномерного движения вдоль оси x:

s_x = υ_xt или x – x₀ = υ_xt.
4.3 Преобразования Галилея

Всякое событие характеризуется координатами места, в котором оно произошло, и моментом времени, когда оно произошло, измеренными в определенной системе отсчета. Иными словами, событие характеризуется четырьмя координатами (x, y, z; t).

Если одна система отсчета движется относительно другой равномерно и прямолинейно со скоростью V (для определенности, эта скорость направлена вдоль оси x), то координаты одного и того же события в этих системах связаны соотношениями:

t = t',

x = x' + Vt',

y = y',

z = z'.

В векторной форме записи:
t = t', = +t'.
Здесь и – радиусы-векторы произвольной точки Р в двух системах отсчета. Отметим, что в этих формулах предполагается (постулируется), что время события одинаково в любой системе отсчета, равномерно движущейся относительно данной системы.

Если принять, что точка Р движется равномерно и прямолинейно, то = +t, = + t, где и – скорости точки в двух системах отсчета. Если отсюда найти перемещения Δ = t и Δ = t, подставить их в формулу преобразования Галилея и поделить на t, получится закон сложения скоростей в классической механике:

= + .

Скорость принято называть переносной скоростью, - относительной скоростью, - абсолютной скоростью. В общем случае эти скорости могут иметь различные направления.

Этот закон, конечно, верен не только для равномерного, но и для произвольного движения. Таким образом, скорость тела относительно (условно) неподвижной системы отсчета 1 равна векторной сумме скорости тела относительно движущейся системы отсчета 2 и скорости движения самой системы 2 относительно системы 1.

Абсолютная скорость тела равна векторной сумме его относительной скорости и переносной скорости подвижной системы отсчета.

Примером может служить движение лодки по реке. Скорость лодки относительно берегов является векторной суммой скорости лодки относительно воды и скорости течения воды.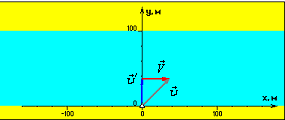



Рисунок 5 Иллюстрация к закону сложения скоростей

4.4 Кинематика прямолинейного равноускоренного движения
Мгновенная скорость неравномерного движения
(8)

При уменьшении величины интервала Δt = t₂ – t₁ вектор Δ = все точнее совпадает с вектором касательной в точке, отвечающей моменту времени t₁. Таким образом, вектор (t) в каждой точке траектории (т.е. в каждый момент времени) направлен по касательной к траектории в этой точке.

Ускорение неравномерного движения
(9)

Направление вектора ускорения совпадает с направлением вектора изменения скорости за малый промежуток времени.

Когда тело движется с переменной скоростью по криволинейной траектории, то направление ускорения по отношению к направлению скорости зависит от того, как меняется скорость:

а) скорость возрастает, вектор ускорения образует острый угол с вектором скорости;

б) скорость не меняется по величине, ускорение перпендикулярно скорости или равно нулю;

в) скорость убывает, вектор ускорения образует тупой угол с вектором скорости.

В любом случае вектор ускорения при движении по криволинейной траектории всегда имеет отличную от нуля проекцию, направленную в сторону искривления траектории.

Размерность ускорения: [a] = м/с².

Пусть тело движется по прямой с переменной скоростью υ(t). Перемещение тела геометрически есть площадь под кривой υ(t) между двумя фиксированными точками во времени. Аналитически это перемещение определяется как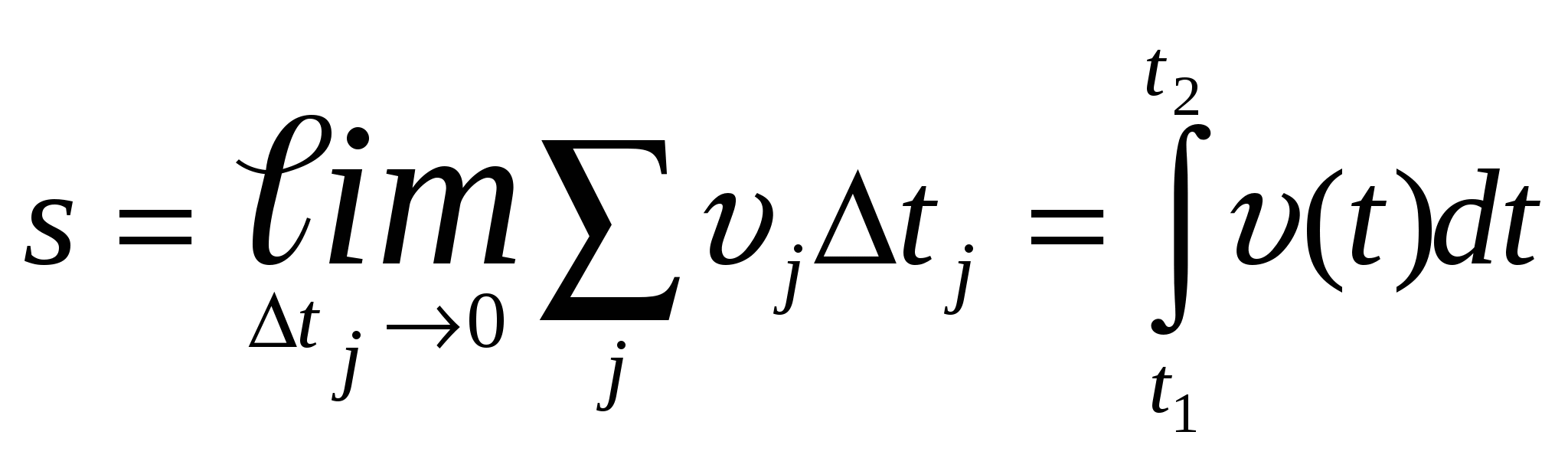

(10)

Если вектор ускорения а постоянен по величине и направлению, то движение называется прямолинейным равноускоренным движением. Если принять направление скорости тела за направление движения и выбрать ось х в эту же сторону, то основные формулы, определяющие равноускоренное движение для проекции на ось OX, примут вид:
a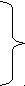_x = const,

υ_x = υ_0x + at, (11)

s_x = υ_0xt + a_xt²/2,

x = x₀ + υ_0xt + a_xt²/2.
Знак проекции ускорения определяет характер движения:
a_x > 0 – равноускоренное;

a_x < 0 – равнозамедленное.
Если исключить время t из уравнений для скорости υ и перемещения s прямолинейного равноускоренного движения, то получается формула, связывающая проекцию перемещения, скорость и ускорение (эта формула, конечно, верна при любом знаке a):

= + 2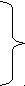a_xs_x. (12)

Уравнения равноускоренного прямолинейного движения в векторной форме:



(13)



Важным случаем равноускоренного движения является свободное падение в поле тяжести Земли с постоянным ускорением g≈9,8 м/с².

Для описания такого движения удобно выбрать систему координат с осью y, направленной вертикально вверх. Тогда вектор ускорения = –g направлен вертикально вниз. Основные формулы принимают вид:




a_y = – g,

υ _y(t) = υ_y0 – gt, (14)

y(t) = y₀ + υ _y0t – gt²/2.
Эти формулы в равной степени справедливы как для случая падения тела с некоторой высоты, так и для случая бросания тела вверх с некоторой начальной скоростью.

Пусть y₀ = 0, υ_y0 = υ₀ (тело брошено вертикально вверх с нулевой высоты в момент времени t = 0). В момент достижения максимальной высоты υ_y = 0. Этому соответствует момент времени, определяемый из уравнения:

0 = υ_y0 – gt*. (15)

Итак, время движения брошенного вверх тела до достижения максимальной высоты (время подъема)
t* = υ ₀/g. (16)

Максимальная высота равна
(17)
4.5 Кинематика равномерного вращения по окружности

При движении по окружности с постоянной по величине линейной скоростью υ тело имеет направленное к центру окружности постоянное центростремительное ускорение
a_ц = υ²/R, (18)
где R – радиус окружности.