Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда. Второй закон Ньютона. Движение под действием постоянной силы. Минобрнауки россии

• Название: Минобрнауки россии
• Анкор: Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда.doc
• Дата: 02.02.2017
• Размер: 0.55 Mb.
• Имя файла: Второй закон Ньютона. Движение под действием постоянной силы. Ма.doc
• Тип: Методические указания; #1757
• страница: 3 из 3

Рисунок 11 Принципиальная схема установки с учётом силы трения и размеров блока и оси блока

Момент силы трения в оси блока M_tp= F_tpr, где F_tp — сила трения между блоком и осью, r— радиус оси.

Сила трения F_тр между блоком и осью пропорциональна силе давления на оси блока. Тогда

N=T₁+T₂==(2M+m₀)g (39)

F_тр=μN=μ(2M+m₀)g,

где μ— коэффициент трения между блоком и осью, зависящий от свойств соприкасающихся поверхностей втулки блока и оси. Таким образом, момент силы трения в оси блока

(40)

Обозначим ε₀=m₀/(2M). Подставим (40) в (38):

(41)

Как видно из (41), значение ε₀ не может быть сколь угодно малым. Оно определяется конструкцией блока (например, его радиусами R и r) и коэффициентом трения между блоком и осью.

Так как в машине Атвуда m₀<< М, то ε₀<<1 и

ε₀ ≈μr/R

Какое же значение ε₀ можно ожидать? Типичное значение коэффициента трения μ 10^-2  10^-1. На наших установках r/R 10^-2  10^-1. Таким образом, ε₀ 10^-4  10^-2. Мы привели лишь правдоподобные рассуждения о том, каким может быть ε₀. Существенно то, что ε₀ можно оценить экспериментально. Например, на установке с грузами массой М = 86 г перегрузок массой 1г не страгивает блока, а перегрузок массой 2 г приводит блок в движение. Это значит, что



В таком случае оценить ε₀, характеризующую установку, можно лишь по порядку величины. Как оказывается, она порядка 10^-2. Интуитивно ясно, что трением можно пренебречь, если масса перегрузка т  m₀.

Действительно, если масса перегрузка чуть больше m₀, то трение в оси блока будет решающим образом определять движение грузов. Это движение уже не будет равноускоренным. Может даже случиться, что система будет двигаться рывками, т. е. остановится, затем снова придет в движение и т. д.

Таким образом, при т m₀, т. е. при ε ε₀, формула (36) становится неверной. Можно ожидать, что при ε ε₀ она достаточно точно описывает реальную ситуацию. Так как ε₀10^-2, то оптимальное значение ε 10^-1. Это значит, что экспериментировать надо с перегрузками 5—20г (при М = 86 г). Если взять ε 1, то а g. Мы приходим к случаю почти свободного падения.

Можно показать, (см. контрольный вопрос 2), что относительная погрешность при определении ускорения грузов, связанная с пренебрежением массой блока и трением, равна



где m_б— масса блока.

Так как величины m₀/т и m_б /(2М) одного и того же порядка 10^-1, то и относительная погрешность при измерении ускорения 10^-1. Очевидно, что такого же порядка будет и относ тельная погрешность при измерении g.

4.14 Методика измерений

В первую очередь необходимо определить минимальную массу перегрузка m₀ страгивающего блок, с тем, чтобы в дальнейшем проводить измерения с грузами, в 5—10 раз превышающими массу m₀. Только в этом случае можно пренебречь влиянием трения на движение системы. Не следует стремиться определить m₀ точно, достаточно получить ее правильную оценку «сверху», например, выяснить, что m₀ не превышает 1 г или 2 г. Для определения m₀ можно постепенно увеличивать массу перегрузка, пока блок придет в движение. Так как блок не может быть отцентрирован идеально, то может оказаться, что в различных начальных положениях блока массы страгивающего перегрузка различны. Поэтому нужно повторить измерения m₀, в разных положениях блока, а затем в качестве оценки для m₀ взять наибольшее из найденных значений.

Следует убедиться, что движение системы при достаточно большой фиксированной массе перегрузка m >>m₀ является равноускоренным. Для этого нужно экспериментально проверить выполнение зависимости h = аt²/2. Удобно переписать это соотношение в виде

(42)

из которого ясно, что в осях координат х = , у = t прямая t= t(), проходящая через начало координат, соответствует равноускоренному движению.

Прямая t () может быть построена по экспериментальным точкам: для одного перегрузка m и ряда различных значений высоты h измеряется время падения груза. Измерения времени для каждой высоты производятся несколько раз, результаты усредняются и записываются в виде

t =,

где — среднее арифметическое значение измеренного времени падения для данной высоты. В условиях эксперимента погрешность t оказывается заметно превышающей погрешность в показаниях электронного миллисекундомера (Dt)₀, а именно:

Dt>>(Dt)₀=10^-3 с.

Поэтому было бы грубой ошибкой считать, что погрешность определения времени падения равна 10^-3 с.

Для построения графика на оси ординат откладываются измеренные значения с указанием погрешности

(43)

где n — число измерений, t_i — результат i-гo измерения.

На оси абсцисс откладывается . Если полученные экспериментальные точки ложатся на прямую, то движение системы можно считать равноускоренным.

Наконец, важно выяснить, подтверждается ли на опыте зависимость времени падения от массы m перегрузка [см. (2)]:

(44)

В осях координат х =, y=t функция t == t () является уравнением прямой. Зависимость t=t () при фиксированной высоте падения h может быть построена по экспериментальным точкам: для нескольких значений массы перегрузка определяется время падения t = ± t.

Измерение времени падения при каждом m повторяют несколько раз, результаты усредняют и находят среднее значение и разброс Dt. Полученные экспериментальные данные откладывают на осях координат на оси ординат — значения с указанием погрешности Dt, на оси абсцисс — соответствующие значения . Затем через полученные точки проводится прямая, и по ее наклону определяется значение g.
5 Порядок выполнения работы

1. Определите массу m₀ страгивающего перегрузка. Для этого, постепенно увеличивая массу т перегрузка, определите с точностью до 0,5 г значение m₀ , начиная с которого блок приходит в движение. Измерения повторите при четырех положениях блока, каждый раз поворачивая блок примерно на 90° по отношению к предыдущему положению. В качестве m₀ следует принять наибольшее из найденных значений.

2. Определите экспериментально зависимость времени падения t груза от высоты h. Измерения проведите при определенном выбранном значении массы перегрузка т = (5  10) m₀. При этом необходимо также, чтобы выполнялось неравенство

m₀<<2М= 172г.

Определите время падения t для четырех-пяти высот h, повторяя измерения для каждого значения h. по четыре раза. Результаты занесите в табл. 1.
Таблица 1 Зависимость времени падения t от высоты h

h, м	t1, с	t2, с	t3, с	t4, с	, с	Dt, с	h, м	m, кг	m0, кг

Здесь t₁,…, t₄ – результаты измерения падения с установленной высоты h:

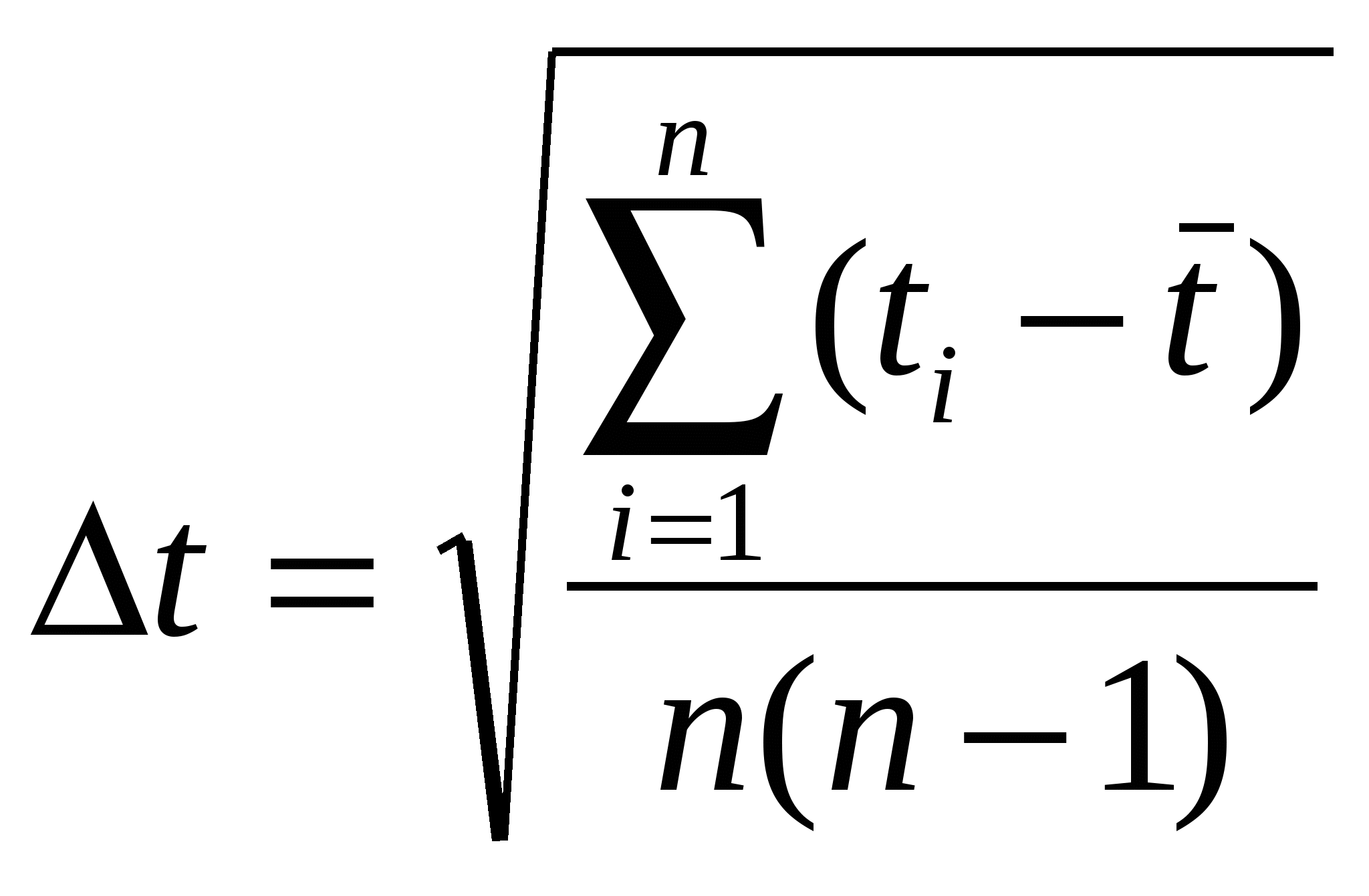, (45)

По результатам измерений в осях координат х = , у = t постройте прямую t= t(). По наклону прямой определите а.



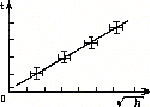
Рисунок 12 Примерный вид графика прямой t= t() в осях координат х = , у = t

3. Определите опытным путём зависимость времени падения t от массы mперегрузка. Измерения проводите при наибольшей возможной высоте падения h = h_mах для пяти значений массы т. Для каждого значения т повторите измерения четыре раза, результаты занесите в таблицу 2.

Таблица 2Зависимость времени падения t от массы m перегрузка

m, кг	М/ m	t1, с	t2, с	t3, с	t4, с	, с	Dt, с

Вce значения массы т перегрузка должны лежать в диапазоне

m₀<<m<< 2М= 172г.

В нашей лабораторной установке точность mопределения массы по существу совпадает со значением массы m₀ страгивающего перегрузка.

По результатам измерений в осях координат х = , у= t постройте прямую t = t () (рисунок 12).



Рисунок 12 Примерный вид графика прямой t = t () в осях координат х = , у = t
По наклону прямой с помощью соотношения (44) определите ускорение свободного падения g и погрешность Dg
6 Содержание отчета

1. 
   Название лабораторной работы.
   
2. 
   Цель лабораторной работы.
   
3. 
   Краткое описание оборудования.
   
4. 
   Рисунок 10. Схема установки.
   
5. 
   Краткое описание хода работы.
   
6. 
   Рисунок 11. Принципиальная схема установки с учётом силы трения и размеров блока и оси блока
   
7. 
   Таблица 1.
   
8. 
   По результатам измерений в осях координат х =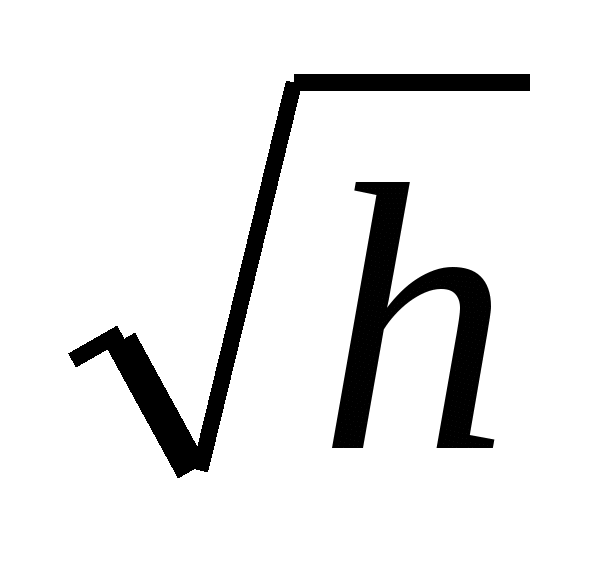 , у = t постройте прямую t= t(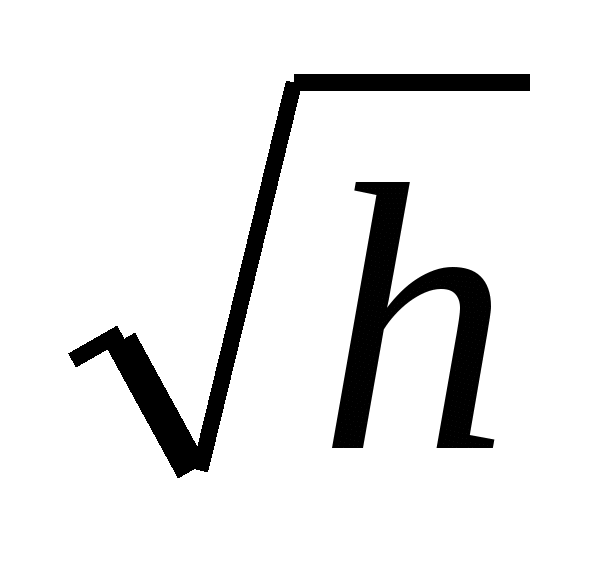). По наклону прямой определите а. (формула (42)).
   
9. 
   Таблица 2.
   
10. 
    По результатам измерений в осях координат х =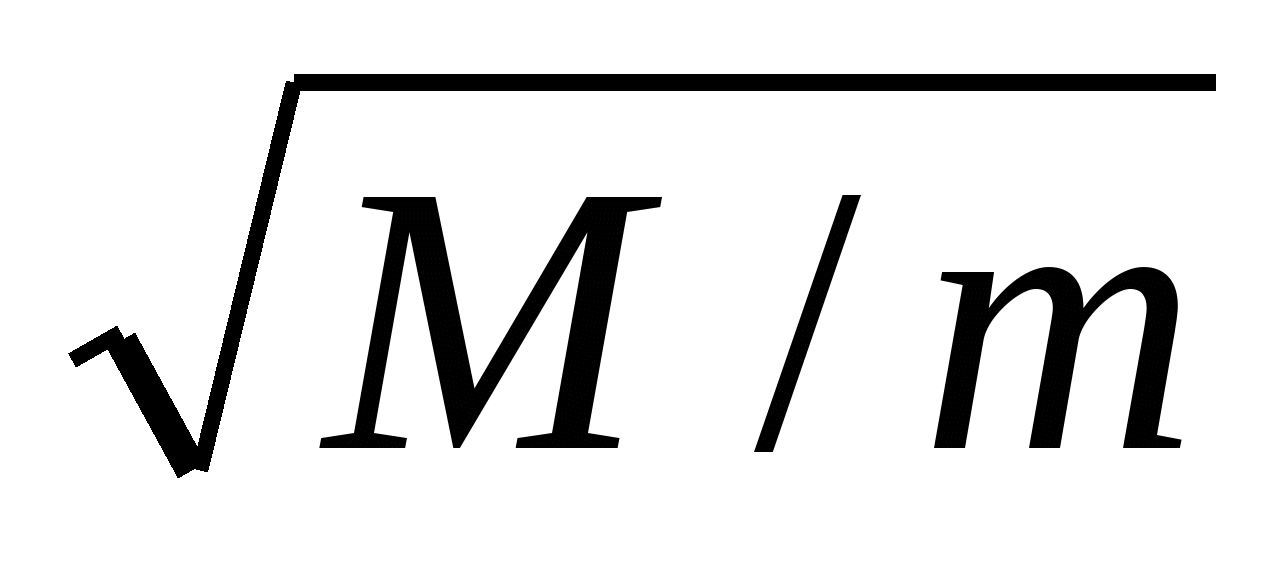 , у= t постройте прямую t = t ().
    
11. 
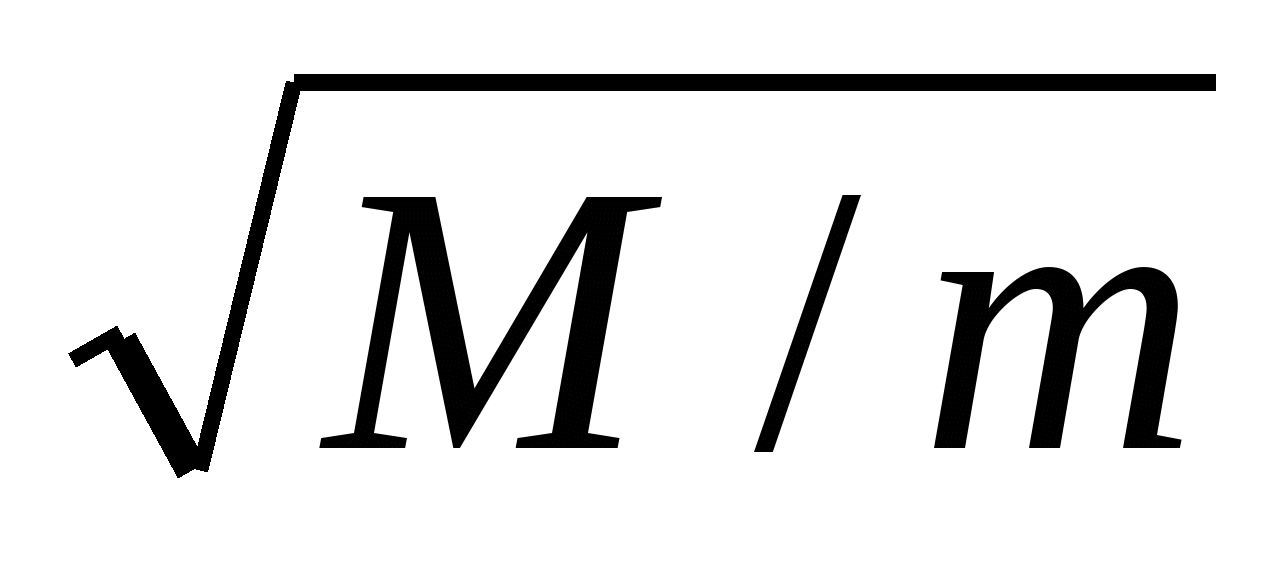    . По наклону прямой с помощью соотношения (44) определите ускорение свободного падения g и погрешность Dg.
    
12. 
    Сделайте вывод. Запишите полученный результат в виде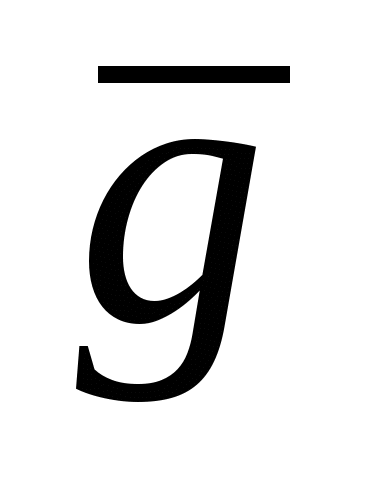 g=±Δg
    

7 Контрольные вопросы и задания

1. 
   Что такое механическое движение, поступательное и вращательное движения?
   
2. 
   Что такое материальная точка и система отсчёта? Отличаются ли длина пути от перемещения?
   
3. 
   Уравнения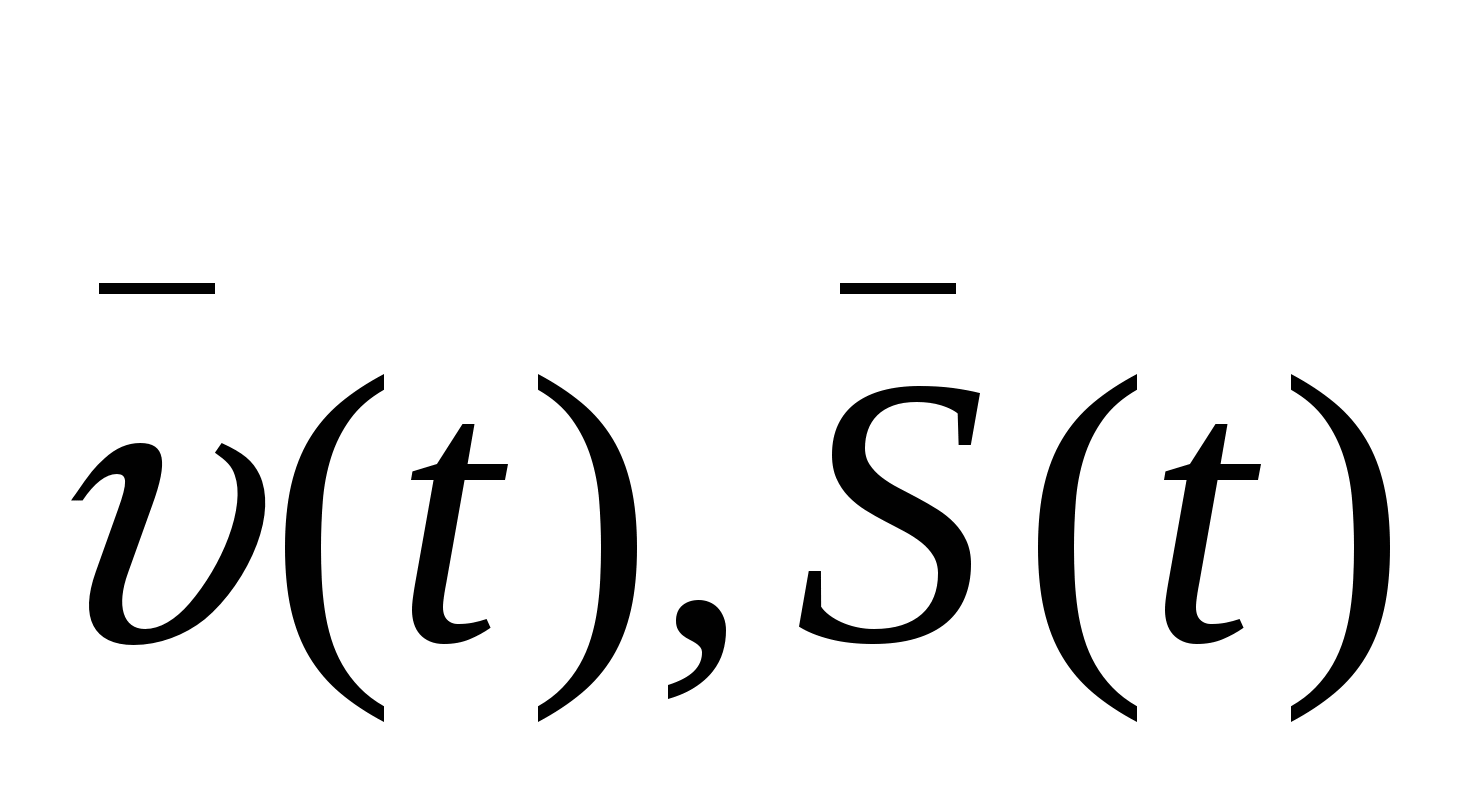 при прямолинейном равномерном движении?
   
4. 
   Уравнения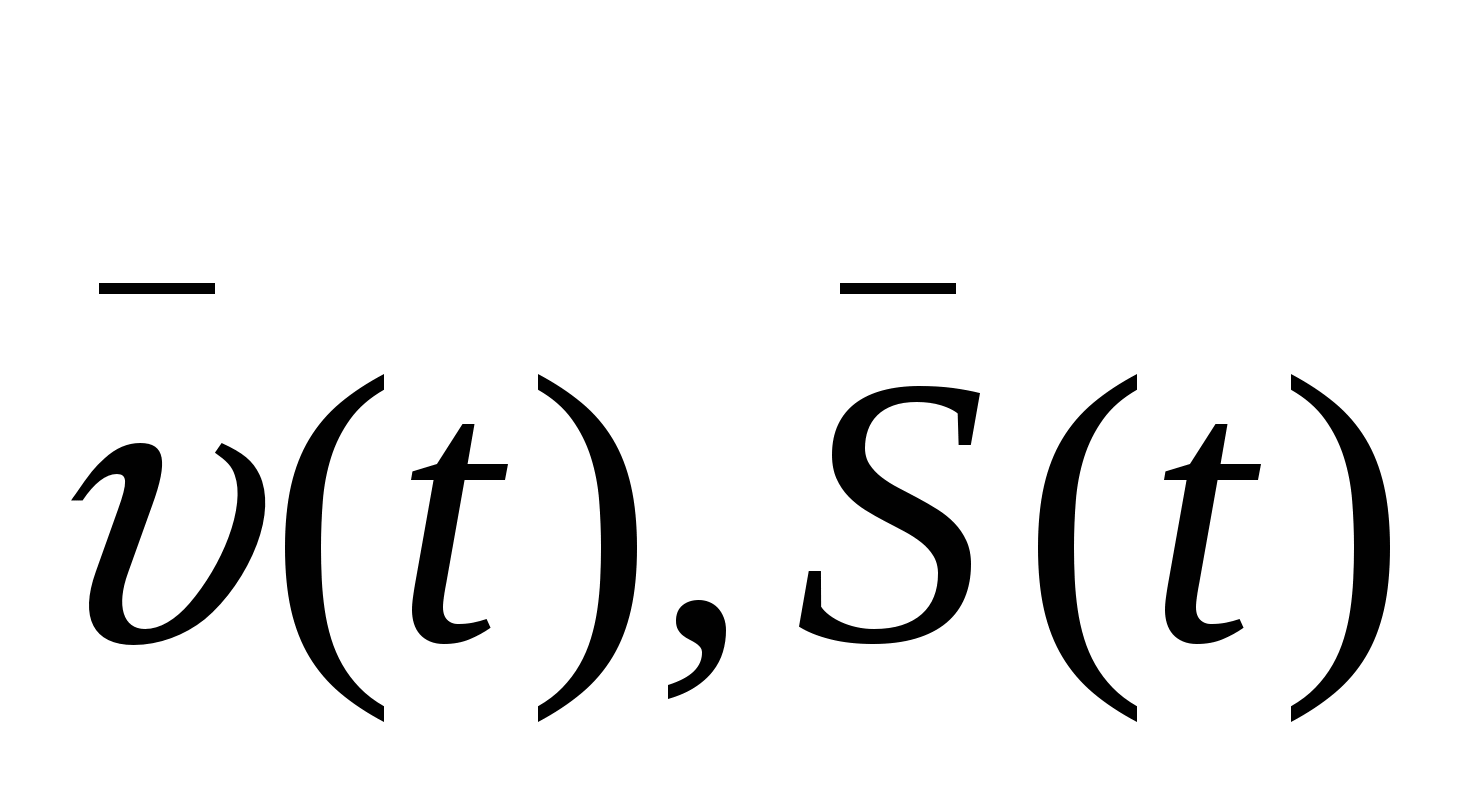 в равноускоренном движении.
   
5. 
   Ускорение и его составляющие?
   
6. 
   Что такое угловая скорость и угловое ускорение?
   
7. 
   Первый закон Ньютона. Масса и сила.
   
8. 
   Сформулируйте законы Ньютона. Запишите формулы (математическую запись) законов Ньютона.
   
9. 
   Дайте определение момента силы, момента инерции, линейного и углового ускорений. Выведите связь линейного и углового ускорений.
   
10. 
    Что такое силы трения?
    
11. 
    Условия равновесия тел имеющих ось вращения
    
12. 
    Закон сохранения количества движения Центр масс.
    
13. 
    Энергия, работа и мощность механического движения?
    
14. 
    Сформулируйте законы сохранения импульса и энергии?
    
15. 
    Какова относительная погрешность измерения g?
    
16. 
    Условия равновесия тел имеющих ось вращения.
    
17. 
    Трамвай, трогаясь с места, движется с постоянным ускорением =0,5 м/с². через t=12 сек. После начала движения мотор трамвая выключается и трамвай движется до остановки равнозамедленно. На всем пути движения трамвая коэффициент трения равен R=0,01. Найти: 1) наибольшую скорость движения трамвая: 2) общую продолжительность движения: 3) ускорение трамвая при равнозамедленном движении: 4) общее расстояние пройденное трамваем.
    
18. 
    Две гири М₁=М₂=1 кг соединены нитью и перекинуты через невесомый блок. На один из грузов кладут перегрузок m=100 г. Найти: 1) ускорение с которым движутся грузы: 2) натяжение нити: 3) силу давления на ось блока. Трением в блоке и весом нити пренебречь.
    

8 Литература

1. 
   Гладун А.Д., Александров Д.А., Игошин Ф.Ф. и др. «Лабораторный практикум по общей физике: В 3 тт: Т. 1: Термодинамика и молекулярная физика (2 семестр): Учебное пособие для студентов 1 курса вузов (под ред. Гладуна А.Д.)» - М.: Издательство МФТИ, 2003 – 316 с. ил
   
2. 
   Трофимова Т. И. Курс физики: Учеб. пособие для вузов. – 13-е изд., стереотип. - М.: Издательский центр «Академия», 2007. – 560 с.: ил.
   
3. 
   Второй закон Ньютона. Движение под действием постоянной силы. Машина Атвуда , Метод. указания к лаб. работам/ Сост. В.Ю. Никифоров – Егорьевск: Егорьевск: ЕТИ МГТУ "Станкин", 2004- 24 с.