реферат. Реферат. Многофакторные эксперименты

• Название: Многофакторные эксперименты
• Анкор: реферат
• Дата: 28.03.2021
• Размер: 136.12 Kb.
• Имя файла: Реферат.docx
• Тип: Курсовая; #188899
• страница: 4 из 4

 + b₂₃   + b₁₃   + b₁₂₃   .

Для оценки коэффициентов данного полинома используются методы линейной регрессии. ПФЭ дает возможность определить коэффициенты регрессии, соответствующие не только линейным членам полинома, но и эффектам взаимодействия порядка выше первого.

План ПФЭ
№ опыта									Реакция y
1	+1	-1	-1	-1	+1	+1	+1	-1	y1
2	+1	-1	-1	+1	+1	-1	-1	+1	y2
3	+1	-1	+1	-1	-1	-1	+1	+1	y3
4	+1	-1	+1	+1	-1	+1	-1	-1	y4
5	+1	+1	-1	-1	-1	+1	-1	+1	y5
6	+1	+1	-1	+1	-1	-1	+1	-1	y6
7	+1	+1	+1	-1	+1	-1	-1	-1	y7
8	+1	+1	+1	+1	+1	+1	+1	+1	y8

Количество испытаний в ПФЭ обладает избыточностью, т.к. значительно превосходит число коэффициентов при линейных членах полинома. Чтобы перейти к ДФЭ, нужно исключить взаимодействия, которыми можно пренебречь:

· фактор    (не изменяется),

·   , т.к. фактор    не изменяется,

·   , т.к. фактор    не изменяется,

·   .

Матрица планирования преобразуется следующим образом:

·   -> 

·    -> 

В матрице необходимо оставить только те строки, в которых значения из столбца   совпадают со значениями из столбца  , а значения из столбца   совпадают со значениями из столбца   .

Матрица ДФЭ имеет следующий вид:

 

 

План ДФЭ
№ опыта	=				Реакция y	Ti
1	+1	-1	-1	+1	y1	18
2	+1	-1	+1	-1	y2	4
3	+1	+1	-1	-1	y3	17
4	+1	+1	+1	+1	y4	5

Проведение эксперимента в i-й точке факторного пространства выполняется следующим образом:

1. По нормированным значениям факторов i-й строки плана эксперимента определяем натуральные значения факторов:

X_Ni=||x_1Ni, x_2Ni,…, x_nNi||, i – номер эксперимента.

2. Устанавливаем факторы на уровни, соответствующие координатам точки факторного пространства X_Ni.

3. Проводим эксперимент, в результате которого определяем отклик системы Y_Ni (T_i – среднее время пребывания заявки с СМО с ограниченной очередью) при выбранных уровнях факторов и заносим значения в таблицу.

4. Используя метод наименьших квадратов, определим коэффициенты регрессионной модели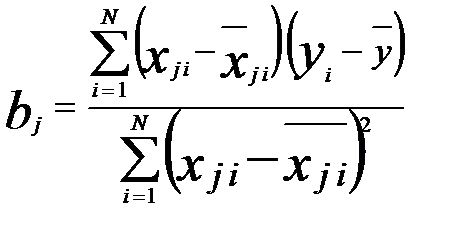

 

   , где                             (1)

                                                                                        

  –номер фактора,

  – номер эксперимента.

Формулу (1) можно упростить, используя кодированные значения уровней факторов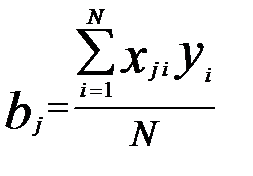

 , где                                                         (2)

                                                                                             

  –номер фактора,

  – номер эксперимента.

5. Согласно формуле (2) по нормированным значениям факторов i-й строки плана эксперимента суммируем значения реакции, полученные при выбранных уровнях факторов. Полученный результат делим на число опытов в эксперименте.

b₀ = (4+17+5+18)/4 = 11,

b₁ = (-4+17-5-18)/4 = 0,

b₂ = (4-17+5-18)/4 = -6.5,

b₃ = (-4-17+5+18)/4 = 0.5.

Подставив вычисленные коэффициенты в аппроксимирующий полином, получим модель планирования эксперимента.

y = 11 – 6.5x₂ + 0.5x₃.

Анализируя полученное выражение, можно сделать вывод, что на реакцию системы (время обслуживания заявки) в наибольшей степени влияет фактор x₂. Знак минус перед ним указывает, что при увеличении значения этого фактора реакция системы уменьшается.