реферат. Реферат. Многофакторные эксперименты
 Скачать 136.12 Kb.
|
|
Таблица 6.5
В этом случае коэффициент  также может быть вычислен по формуле (6.2.7): . (6.2.7)Столбцы  ,  задают планирование эксперимента – по ним определяют результаты опыта; столбцы  ,  служат только для расчета.С ростом числа факторов число возможных взаимодействий возрастает. Например, для факторного эксперимента  кроме , ,  ,  в матрице планирования появляются столбцы ,  ,  ,  . Всего в матрице планирования оказывается восемь столбцов, следовательно, необходимо определять восемь коэффициентов. Все восемь коэффициентов необходимо определять в том случае, если учитывать смешанное взаимодействие. Если же модель задается в виде гиперплоскости (линейная модель), то достаточно определить четыре коэффициента: ,  , , . Полный факторный эксперимент оказывается избыточным и у экспериментатора возникает выбор:1. Построить гиперплоскость по четырем экспериментам, а остальные четыре опыта использовать для оценки погрешности. 2. Провести эксперимент, состоящий из 4-х опытов, то есть реализовать экономный план эксперимента. Таким образом, в отличие от модели гиперболоида, которая требует определение  неизвестных коэффициентов, модель гиперплоскости, содержит  коэффициент и требует соответствующего числа опытов, то есть полный факторный план (ПФП) для модели гиперплоскости сильно избыточен.Для построения гиперплоскости, следовательно, достаточно использовать лишь некоторую часть из ПФП. Эту часть в теории планирования эксперимента называют дробнойрепликой или дробным факторным планом (ДФП). Если дробление ПФП производится последовательным делением числа опытов на 2, то реплику называют регулярной. Число  последовательного деления называют дробностью реплики.Число опытов регулярного ДФП равняется  . При  ДФП называют полурепликой (или 1/2 реплика), при  – 1/4 реплика и т.д.Соответствующее число опытов и параметров планирования приведены в таблице 6.6. Таблица 6.6
Для составления планов-таблиц регулярных дробных реплик часто используют так называемое правило двоичного кода. Оно гласит, что для модели в виде гиперболоида знаки “+” и “–“ в столбцах плана должны чередоваться по правилу чередования двоичных чисел в разряде двоичного кода, то есть в столбце - через 1, в столбце - через 2, в столбце - через 4, в столбце  - через  .Проведение экспериментов и обработка результатов. Так как эксперимент содержит элемент неопределенности вследствие ограниченности обрабатываемых данных, то расстановка повторных или параллельных опытов не дает полностью совпадающих результатов. Получаемая погрешность (воспроизводимости) оценивается стандартными методами усреднения, то есть  ,где  – число параллельных опытов.В этом случае дисперсия равна  . (6.2.8)Если учесть, что матрица планирования состоит из серии опытов, то оценка дисперсии всего эксперимента получается в результате усреднения дисперсии всех опытов. В этом случае говорят о дисперсии воспроизводимости не одного опыта, а эксперимента в целом. Такая дисперсия равна 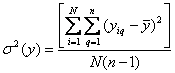 , (6.2.9)где  – число различных опытов (число элементов в матрице планирования);  – число повторных опытов.Формула (6.2.9) справедлива, если соблюдается равенство числа повторных опытов во всех экспериментальных точках матрицы планирования. На практике в разных точках бывает выполнено разное число опытов. В этом случае для оценки дисперсии воспроизводимости пользуются средневзвешенным значением  , (6.2.10)где  – оценка дисперсии  -го опыта,  – число степеней свободы в -ом опыте; это число рассчитывают как  (число параллельных опытов минус 1).Пример. Необходимо провести эксперимент по исследованию характеристик одноканальной СМО (системы массового обслуживания). Построить план эксперимента, описать модель планирования, оценить коэффициенты модели. Параметры исследуемой системы: λ = 15 с-1 – интенсивность поступления заявок,  = 10 с-1 – интенсивность обслуживания,L = 10 – емкость накопителя заявок. В имитационном эксперименте необходимо оценить T – среднее время обслуживания заявки в системе при минимальных затратах ресурсов. 1. Выделим следующие факторы и отклик для составления плана эксперимента: x1= λ, x2 =  ,x3 = L, y = T. 2. Определим локальную подобласть планирования за счет выбора основного (нулевого) уровня каждого фактора xi0, i=  и интервалов варьирования каждого фактора.
Т.к. каждый из k факторов варьируется на двух уровнях, план эксперимента 2k содержит N=2k возможных испытаний: k=3, q=2, N = 23. Для определения зависимости  между откликом системы и уровнями факторов построим аналитическую модель в виде полинома первого порядка:y=b0+b1  +b2  +b3  +b12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
