реферат. Реферат. Многофакторные эксперименты
 Скачать 136.12 Kb.
|
Основы планирования многофакторного эксперимента Рис.6.1 Представление объекта в виде такой схемы основано на принципе «черного ящика». Имеем следующие группы параметров: 1) управляющие (входные)  , которые называются факторами;2) выходные параметры  , которые называются параметрами состояния;3)  - возмущающие воздействия.Предполагается, что возмущающие воздействия не поддаются контролю и либо являются случайными, либо меняются во времени. Каждый фактор имеет область определения, которая должна быть установлена до проведения эксперимента.Комбинацию факторов можно представить как точку в многомерном пространстве, характеризующую состояние системы. На практике целью многофакторного эксперимента является установление зависимости  , (6.2.1)описывающей поведение объекта. Чаще всего функция (6.2.1) строится в виде полинома  (6.2.2)или  . (6.2.3)Целью эксперимента может быть, например, построение зависимости (6.2.1) при минимальном количестве измерений значений управляющих параметров .На первом этапе планирования эксперимента необходимо выбрать область определения факторов . Выбор этой области производится исходя из априорной информации. Значения называются уровнями управляющего параметра.Если выбрана линейная модель (6.2.2), то для построения аппроксимирующей функции достаточно выбрать основной уровень и интервал варьирования управляющего параметра .Для линейной модели интервал варьирования можно определить как  ,а основной (нулевой) уровень - как среднее значение  .Для упрощения планирования эксперимента принято вместо реальных (натуральных) уровней использовать кодированные значения факторов. Для факторов с непрерывной областью определения это можно сделать при помощи следующего преобразования ,где  - натуральное значение фактора;  - интервал варьирования;  - основной уровень;  - кодированное значение. В результате принимает значения на границах  , на основном уровне  . Основная проблема состоит в выборе области варьирования, поскольку эта задача является неформализованной.Рассмотрим полный факторный эксперимент на примере линейной модели (6.2.2). Если число факторов  , то для проведения полного факторного эксперимента нужно  опытов, где 2 - число уровней, которого достаточно для построения линейной модели.Условие проведения этого эксперимента можно зафиксировать в матрице планирования (табл.5.3). Таблица 6.3
Таким образом, для двух факторов построение матрицы планирования элементарно. Для большего числа факторов необходимо разработать правила построения таких матриц. Например, при появлении фактора  в табл.6.3 произойдут следующие изменения (табл.6.4): при появлении нового столбца каждая комбинация уровней исходной таблицы проявится дважды.Таблица 6.4
Это не единственный способ расширения матрицы планирования. Используют также перемножение столбцов, правило чередования знаков. Очень важны общие свойства матрицы планирования: 1) симметричность матрицы относительно центра эксперимента:  . Тогда  .2) условие нормировки  , то есть сумма квадратов элементов каждого столбца равна числу опытов.Первые два свойства относятся к построению отдельных столбцов матрицы 3) совокупность столбцов имеет следующее свойство  , где  .4) Ротатабельность. Это означает, что точки (значения факторов) в матрице планирования подбираются так, что точность предсказания выходного параметра должна быть одинакова на равных расстояниях от центра эксперимента (нулевого уровня) и не зависеть от направления. Планирование эксперимента первого порядка для двух переменных. План эксперимента первого порядка для двух переменных показан на рис.6.2. То есть искомая функция  описывается модельно в виде плоскости (6.2.4)или гиперболоида  . (6.2.5)Расположение этой модели в пространстве показано на рис.6.2 поверхностью, проходящей через точки 1 – 2 – 3 – 4. 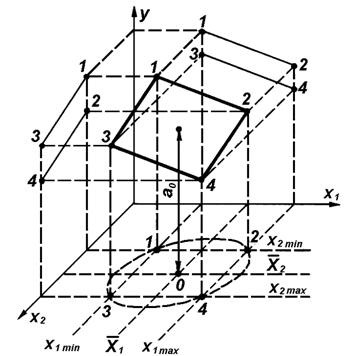 Рис.6.2 Необходимые уровни для полного факторного эксперимента расположены в плоскости  . Для модели в виде гиперболоида этот план является предельно экономным. Для построения гиперболоида необходимо определить четыре коэффициента в модели (6.2.5). Это можно сделать, решая систему из четырех уравнений. Следовательно, необходимы все четыре опыта. В теории планирования эксперимента используется термин насыщенности.Если рассматривать модель (6.2.4) в виде плоскости, то план эксперимента является ненасыщенным (избыточным), так как необходимо определить только три коэффициента  ,  и  . В случае модели (6.2.5) (насыщенный эксперимент) решение системы единственно, и поверхность гиперболоида пройдет через все четыре экспериментальных значения . Следствием этого является то, что насыщенный эксперимент не позволяет усреднить случайные погрешности и не дает сведения об их размере.Для ненасыщенного плана (6.2.4) избыточное число опытов позволяет произвести усреднение и оценить размеры погрешности. Проведя плоскость через точки 1, 2 и 3, можно оценить погрешность, определив, на каком расстоянии от плоскости находится точка 4. Оценка Погрешность в других точках может быть оценена проведением плоскостей 1 – 3 – 4, 1 – 2 – 4 и 2 – 3 – 4. С другой стороны коэффициент наклона поверхности к оси  может быть найден как из наклона прямой 1 – 2, так и из наклона прямой 3 – 4. Аналогично коэффициент при  можно определить из наклона прямых 1 – 3 и 2 – 4.Поскольку полученные таким образом значения  и  могут отличаться, ненасыщенный эксперимент позволяет провести их усреднение и оценить погрешность.Если уравнение плоскости представить в виде  , (6.2.6)где  ;  , то мы переносим начало координат в точку с координатами  . Тогда коэффициент  находится усреднением всех четырех значений как высота центра плоскости 1 – 2 – 3 – 4.Процесс переноса начало координат в центр пространства факторов с координатами  очень важен при обработке данных любых экспериментов, описываемых моделью в виде гиперплоскости, так как позволяет получить более устойчивое усредненное значение для .Важнейшим фактором является то, что в результате такого усреднения построенная плоскость удовлетворяет всем четырем значениям лишь в среднем. В любой точке может быть найдена погрешность отклонения экспериментальных данных относительно модели, и по этим четырем отклонениям можно вычислить СКО.Таким образом, один из четырех опытов является избыточным и может быть исключен. Но тогда план эксперимента становится неротатабельным, то есть неравноточным по всем направлениям. Если исключена точка 4 на рис.6.2, то в направлении 3 – 2 в плоскости факторов будет обеспечена большая точность, чем в направлении 1 - 0. В этом случае для восстановления ротатабельности точки 1, 2 и 3 в плоскости факторов должны быть равноудалены как друг от друга, так и от центра, то есть располагаться в вершинах равностороннего треугольника с центром в точке 0. В общем случае для линейной модели (6.2.4), эксперимент содержащий конечное число опытов позволяет получить только оценки для коэффициентов , и . Подставив в уравнение модели (6.2.4) известные значения факторов  и результаты опытов получим систему линейных алгебраических уравнений для определения  . Если количество этих уравнений больше трех, то значения оценок , и могут быть получены при помощи МНК: , (6.2.7)где  - количество опытов. Здесь учтено, что принимают значения -1,+1.Для вычисления коэффициентов линейной модели по формуле (6.2.7) получим:  , Таким образом, для вычисления и можно использовать (6.2.8). Для определения в формуле (6.2.4) найдем среднее значение  , равное  , где  ,  .В случае симметричности матрицы планирования  , откуда  . Чтобы коэффициент модели вычислялся по единой формуле (6.2.7) в матрице планирования вводят фиктивную переменную  , которая принимает значение  во всех опытах и соответствует коэффициенту . Коэффициент при независимых переменных указывает на силу влияния факторов: чем больше значение имеет коэффициент , тем большее влияние оказывает соответствующий фактор. В этом смысле результат планирования эксперимента алогичны факторному анализу. Для пассивных экспериментов факторный анализ может использоваться в качестве априорных данных при планировании.Планируя эксперимент, стремятся получить линейную модель, однако в выбранных интервалах варьирования априори не известно, что линейная модель адекватно описывает поведение системы. Нелинейность связана со смешанным взаимодействием. Формула (6.2.5) всегда может быть оценена по полному факторному эксперименту. Для полного факторного эксперимента  матрица планирования с учетом эффекта взаимодействия приведена в табл.6.5. |
