Курсовая работа. Многокритериальная параметрическая оптимизация системы регулирования подачи топлива двс
 Скачать 1.65 Mb. Скачать 1.65 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное автономное образовательное учреждение высшего образования «МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»  Факультет: «Машиностроение» Кафедра: «Автоматика и управление» Дисциплина: «Проектирование систем управления» Курсовой проект Тема: «Многокритериальная параметрическая оптимизация системы регулирования подачи топлива ДВС». Группа 181-251 Выполнил: Холодилин Александр Евгеньевич Проверил: Березин Евгений Сергеевич Оглавление2. Выбор и описание системы управленияВначале в соответствии с рекомендациями учебно-методического пособия следует выбрать систему управления и описать ее работу, приведя функциональную схему. Как правило, выбирается система автоматического регулирования (САР) с отрицательной обратной связью – частный случай системы управления. Затем надлежит составить блок-схему САР, задать передаточные функции всех входящих в нее устройств, получить передаточную функцию замкнутой САР, назначить внутренние (варьируемые) параметры и определить область работоспособности. 2.1. Описание системы управления Топливная система автомобиля (или система подачи топлива) — система, предназначенная для подачи топлива (бензина или дизельного топлива) из топливного бака в двигатель (точнее – в карбюратор или форсунки). Также эта система обеспечивает хранение топлива и его очистку перед подачей в двигатель. Независимо от типа, любая топливная система содержит несколько основных компонентов: - Топливный бак; - Система топливопроводов; - Топливный насос; - Топливный фильтр (или фильтры); - Устройство образования топливно-воздушной смеси или устройства впрыска топлива в цилиндры. 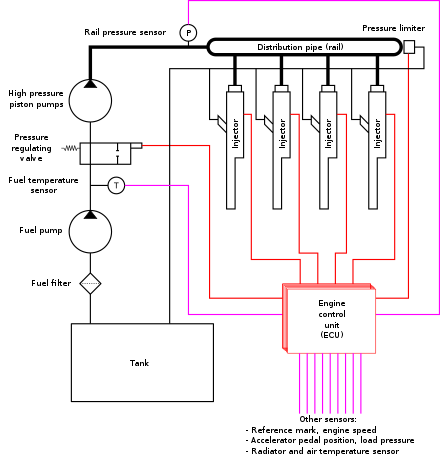 Рис. 2.1. Функциональная схема работы топливной системы ДВС Топливный насос подает топливо в систему впрыска и поддерживает рабочее давление в топливной системе. Топливный насос устанавливается в топливном баке и имеет электрический привод. При необходимости используется дополнительный (подкачивающий) насос (не путать с топливным насосом высокого давления системы впрыска дизельных двигателей и системы непосредственного впрыска). Топливо в системе циркулирует по топливопроводам. Различают подающий и сливной топливопроводы. В подающем топливопроводе поддерживается рабочее давление. По сливному топливопроводу излишки топлива удаляются в топливный бак. Система впрыска предназначена для образования топливно-воздушной смеси за счет впрыска топлива. Работа топливной системы осуществляется следующим образом. При включении зажигания топливный насос закачивает топливо в систему. При прохождении через топливный фильтр происходит его очистка. Далее топливо поступает в систему впрыска, где происходит распыление и образование топливно-воздушной смеси. 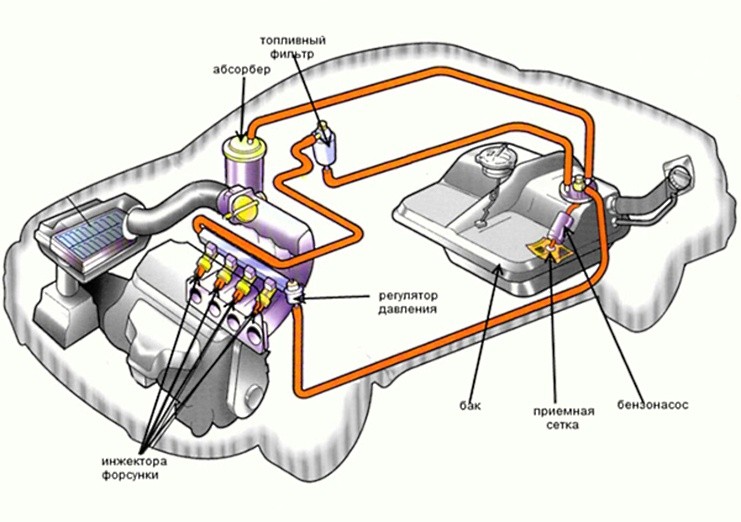 Рис. 2.2. Схема топливной системы автомобиля 2.2. Блок-схема САР При рассмотрении выбранной системы управления необходимо также учитывать показания множества датчиков. Для этого надо ввести математическую модель ДВС в прямую цепь системы управления. Но это приведет к усложнению моделирования и оптимизации, поэтому будем рассматривать упрощенную схему управления подачей топлива ДВС приведенную на рисунке 2.3. 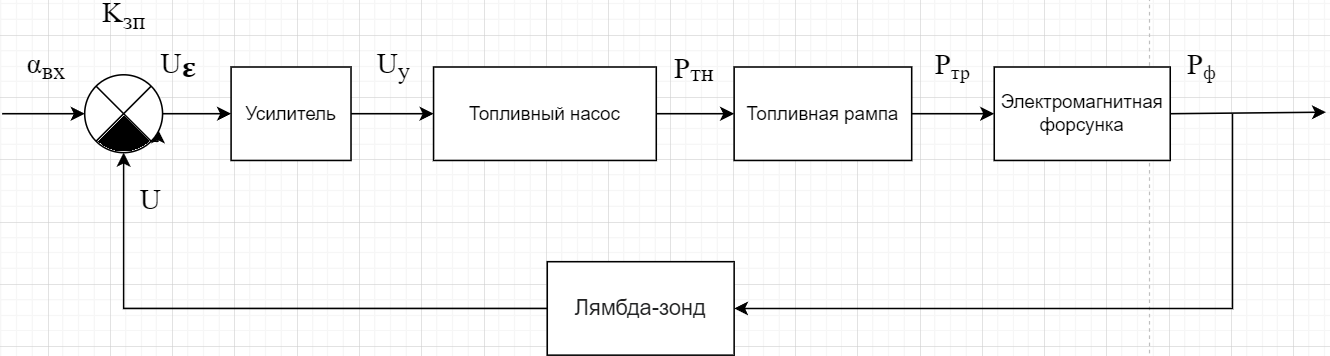 Рис.2.3. Блок-схема поддержания постоянного давления в топливной системе ДВС 3.Математическое описание элементов САР3.1. Задающий потенциометр  Рис.3.1.Схема включения задающего потенциометра Отклонение рычага датчика клиренса влечет за собой изменение выходного напряжения Uвых, которое преобразуется электромеханическим преобразователем (резистивный ИП) из перемещения (рис.3.1). Связь между напряжением, снимаемым с подвижного контакта ИП (Uвых) и углом поворота вала линейным алгебраическим уравнением: Uвых =Kзп ·αвх Следовательно, передаточная функция потенциометра будет иметь вид: Wзп(Uвых/ αвх) = Kзп, где: Kзп = 1 В/рад – коэффициент передачи задающего потенциометра. 3.2 Усилитель  Рис.3.2. Схема неинвертирующего усилителя В этой схеме (рис.3.2) используется также отрицательная ОС по напряжению, но она последовательная: здесь дифференциальное входное напряжение ОУ определяется как разность входного напряжения и напряжения обратной связи (сигнал подается непосредственно на неинвертирующий вход ОУ, а к инвертирующему входу подводится напряжение обратной связи с выхода ОУ). Поскольку напряжение между входами равно нулю, то на инвертирующем входе напряжение равно 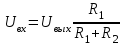 , ,таким образом, коэффициент усиления определяется формулой 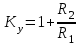 Следовательно, передаточная функция усилителя: Wу(s) = Kу, где Kу = 2,9. 3.3. Топливный насос Топливный насос устанавливается, как правило, в топливном баке. Рабочее колесо (крыльчатка) центробежного насоса снабжено по периметру многочисленными лопатками. Крыльчатка вращается внутри камеры, в которой находятся два канала определенной формы – всасывающий и нагнетательный. Завихрения топлива, возникающие при воздействии на него лопаток, обеспечивают повышение давления. 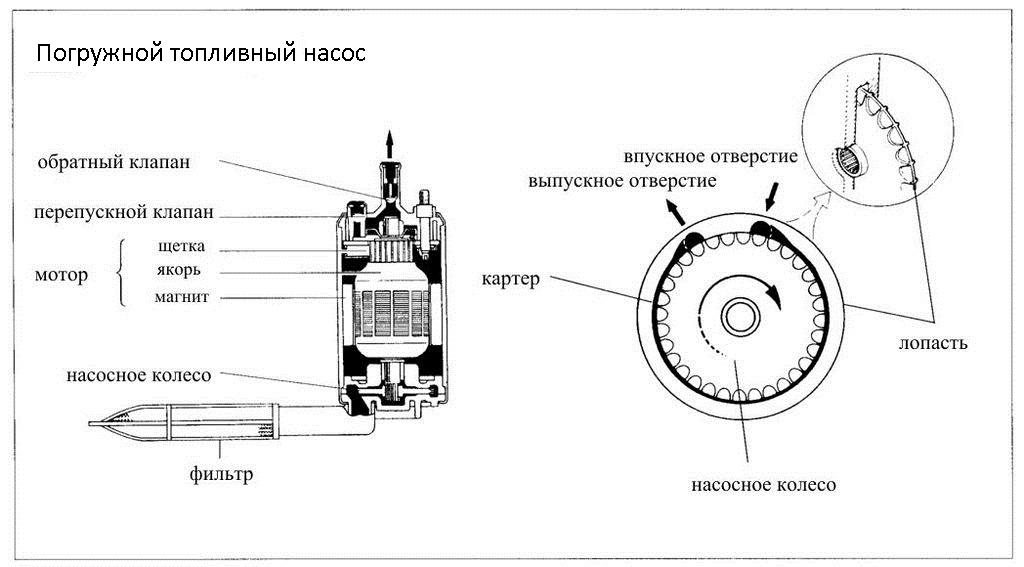 Рис.3.3. Конструкция топливного насоса Передаточная схема электродвигателя: Wдв(s)=K/s(Tмs+1)(Tэs+1). 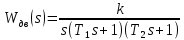 Следовательно, передаточная функция гидронасоса: 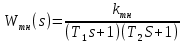 где kтн = 2; Т1 = 0,048с; Т2 = 0,01с. 3.4. Топливная рампа Основу конструкции топливной рампы составляет трубка круглого или прямоугольного сечения, закрепляемая на впускном коллекторе двигателя с помощью болтовых соединений. Рампа служит для подвода находящегося под давлением топлива с его последующим распределением между форсунками, количество которых зависит от числа цилиндров в блоке. Форсунки могут как закрепляться непосредственно на рампе, так и находиться на расстоянии, при этом подача топлива осуществляется по отдельным трубкам. Передаточная функция топливной рампы: 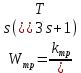 Где T3 = 0.015, Kтр = 1.5 3.5. Электромагнитная форсунка Работа электромагнитной форсунки осуществляется следующим образом. В соответствии с заложенным алгоритмом электронный блок управления обеспечивает в нужный момент подачу напряжения на обмотку возбуждения клапана. При этом создается электромагнитное поле, которое преодолевая усилие пружины, втягивает якорь с иглой и освобождает сопло. Производится впрыск топлива. С исчезновением напряжения, пружина возвращает иглу форсунки на седло. Количество топлива впрыскиваемого в топливный канал ГБЦ зависит от давления в топливной рампе Pтр. ЭБУ считает на какое промежуток времени надо «открыть» форсунку, что бы впрыснуть топливо, находящееся под нужным давлением. 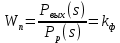 где kф=1. 3.6. Датчик обратной связи В качестве датчика обратной связи используем датчик относительного состава продуктов сгорания, то есть лямбда-зонд, передаточная функция которого выглядит следующим образом: 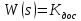 4. Структурная схема САРПо полученным передаточным функциям отдельных устройств получим структурную схему с описанием всех входящих в неё звеньев. Стоит отметить, что САР является астатической 4-го порядка. Это значит, что ошибка регулирования стремится к нулю независимо от размера воздействия, если последнее принимает установившееся постоянное значение. 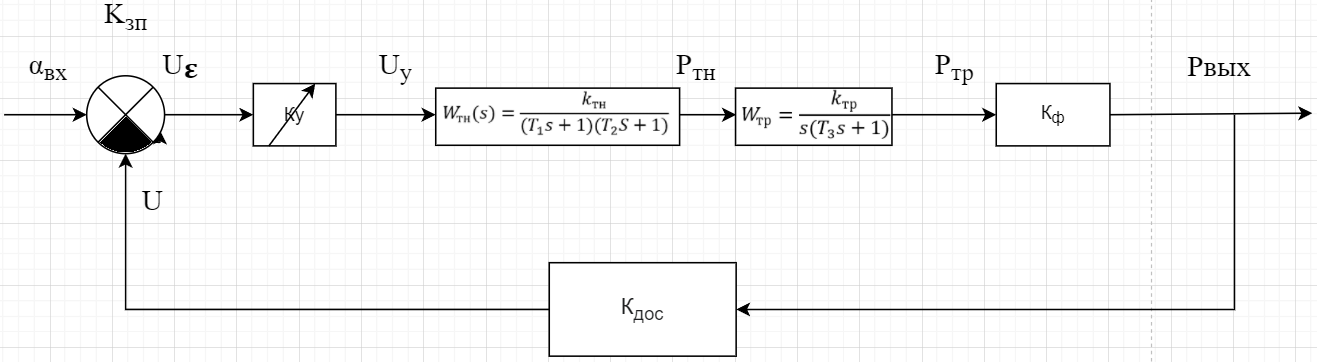 Рис.4.1. Структурная схема поддержания постоянного давления в топливной системе 5. Выбор варьируемых параметровВ процессе проведения оптимизации данной системы изменениям следует подвергнуть только коэффициент передачи усилителя Kу. Другие параметры будут оставаться неизменными, т.к. их варьирование связано с практическим неудобством их реального изменения в системе, которое может повлечь значительные конструктивные изменения. Например, выбрав в качестве варьируемого параметра постоянную времени T1, мы должны иметь в виду, что это может потребовать изменений в конструкции топливного насоса или даже выбора другого типа насоса и т.п., что нецелесообразно. Изменение таких параметров как Т3, Kтр, T1, T2, Kтн, Kф могут потребовать значительных изменений в конструкции топливной системы и ее элементов, а изменение такого параметра как Kу – коэффициент передачи усилителя не повлечет за собой больших конструкторских затрат. Оптимизируем систему по параметру Kу, от этого параметра зависит подача давления топливного насоса. 6. Получение передаточной функции замкнутой системы поддержания давления в топливной системеПередаточная функция разомкнутой системы стабилизации поддержания давления в пневмоэлементах с учетом передаточных функций всех входящих в нее устройств будет иметь вид: 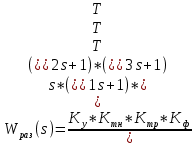 Передаточная функция замкнутой системы с учетом отрицательной обратной связи с коэффициентом 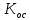 = Кдос =1 будет иметь вид: = Кдос =1 будет иметь вид: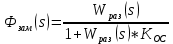 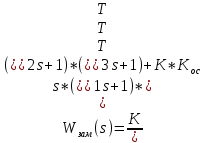 Где 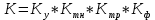 7. Моделирование исходной системыНа рис.4.1 представлена структурная схема поддержания постоянного давления в топливной системе с описанием основных элементов системы в математической форме. Переходная функция исходной системы получена в ПК «МВТУ 3.7» и показана на рис 7.1. 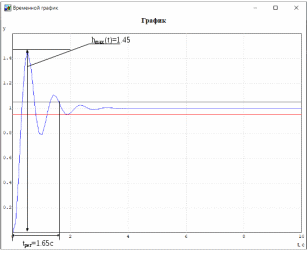 Рис.7.1. Переходная функция исходной системы По графику переходного процесса определяем: - Время регулирования, при котором кривая переходного процесса входит в 5%-ю трубку, определяя завершение переходного процесса (это время характеризует быстродействие системы): tрег= 1.65c. - Коэффициент перерегулирования, который может служить мерой колебательности процесса: 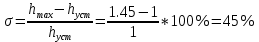 Коэффициент Ку, выбранный в качестве оптимизируемого параметра, в исходной системе равен 2.9. 8. Определение области работоспособностиПоскольку условия работоспособности в задании не оговорены, то будем исходить из самых слабых возможных ограничений. Таковыми, как известно, являются требования устойчивости: если система становится неустойчивой – значит, она перестает быть работоспособной. Поэтому если из условия нахождения системы на границе устойчивости мы получим ограничения на варьируемые параметры, то это и позволит, по существу, определить одну из границ максимально возможной области работоспособности. Другие границы этой области можно определить из других разумных условий: например, обеспечения передачи информационных сигналов между устройствами системы и т.п. Итак, в рассматриваемой системе выбран один варьируемый параметр: коэффициент передачи усилителя Ку, который входит как сомножитель в общий коэффициент передачи разомкнутой системы К. Для того чтобы составить характеристическое уравнение, необходимо приравнять знаменатель передаточной функции замкнутой системы к нулю: 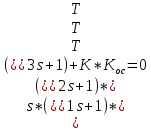 Раскрывая скобки, получаем: 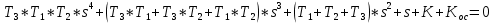 Подставляя значения всех параметров, получим: 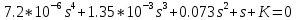 Введем обозначения: 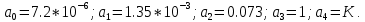 По коэффициентам этого уравнения составим определитель Гурвица и приравняем его к нулю, так как это соответствует границе устойчивости: Составляем матрицу коэффициентов характеристического уравнения исходной системы. 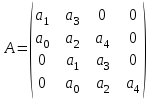 Для устойчивости системы необходимо, чтобы выполнялись условия: ∆1 > 0; ∆2 > 0; ∆3 > 0; ∆4 > 0; Составим определители Гурвица и приравняем нулю, так как это соответствует границе устойчивости. 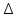 1 = а1 > 0; 1 = а1 > 0;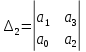 = а1а2 - а3а0 > 0 = а1а2 - а3а0 > 0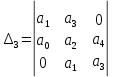 = а3(а1а2 - а3а0) – а4а12> 0 = а3(а1а2 - а3а0) – а4а12> 0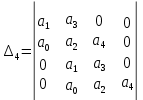 = а4∆3 > 0 = а4∆3 > 0а4∆3 = а4(а3(а1а2 - а3а0) – а4а12) = 0 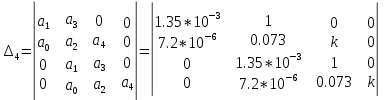 Для нахождения К достаточно вычислить определитель 3-го порядка: 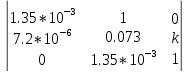 =1*( =1*(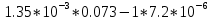 )-K*( )-K*(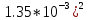 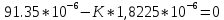 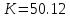 Теперь найдем Ку: 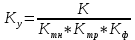 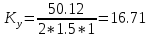 Поскольку варьируемый параметр всего один, то область работоспособности в этом частном случае представляет собой отрезок значений на действительной прямой, т.е. диапазон значений. Верхнее значение диапазона изменения параметра Ку=16.71. Нижнее значение диапазона определим из условия обеспечения передачи информации от устройства к устройству: неразрывности (прямой) цепи. Из этого условия следует, что коэффициенты передачи всех устройств, в том числе и усилителя, должны быть больше нуля. Если хотя бы один из них будет равен нулю, произойдет разрыв цепи, и информация не пройдет на выход системы. Зададим минимальное значение Ку при исследовании системы. Возьмем Ку равным 0.1, т.к. при Ку =0 происходит разрыв системы. Для нормального функционирования, САР должна быть достаточно удалена от границ устойчивости и иметь достаточный запас устойчивости. Необходимость этого обусловлена прежде всего следующими причинами: a) уравнения элементов САР, как правило, идеализированы, при их составлении не учитывают второстепенные факторы; б) при линеаризации уравнения погрешности приближения дополнительно увеличиваются; в) параметры элементов определяются с некоторой погрешностью; г) параметры однотипных элементов имеют технологических разброс; д) при эксплуатации параметры элементов изменяются вследствие старения. Следовательно, устойчивая по расчету САР в действительности может оказаться неустойчивой. Таким образом, Ку 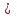 [0.1…16.71]. [0.1…16.71]. 9. Параметрическая оптимизация СУ9.1. Выбор критериев оптимальности Параметрическая оптимизация – это процедура нахождения значений внутренних параметров проектируемого или исследуемого объекта заданной структуры, при которых достигается наилучшее сочетание свойств этого объекта, отображаемое в критерии. Оптимальными называются те параметры, при сочетании которых вероятность выполнения условий работоспособности максимальна. Для нахождения оптимальных параметров системы требуется обеспечить экстремум критерия оптимальности (ЦФ), связанный с показателями динамического качества, за счет варьируемых параметров, допустимые значения которых лежат в заданной области. В качестве варьируемого параметра выбираем коэффициент передачи усилителя Ку, с диапазоном изменения от 0,1 до 16,71. 9.2 Оптимизация по критерию среднеквадратической ошибки Оптимизация проводилась по следующей схеме: 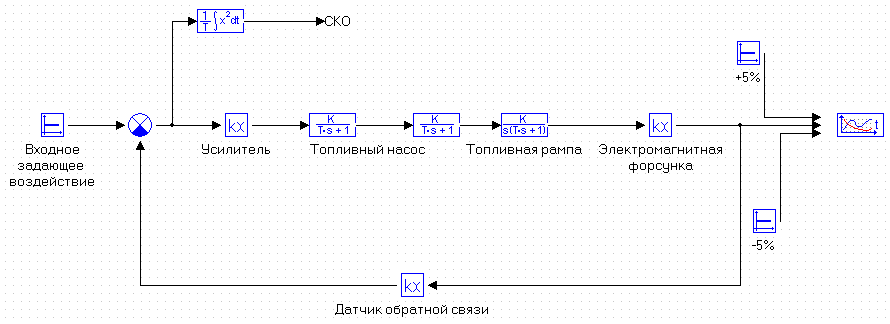 Рис.9.1. Схема моделирования по критерию среднеквадратическая ошибка Целевая функция сформирована на выходе блока: 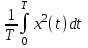 . .Целью оптимизации явилось нахождение минимального значения среднеквадратической ошибки. Коэффициент передачи усилителя Kу изменяем в пределах от 0,1 до 16,71. Оптимизация велась с интервалом неопределенных параметров = 0,1 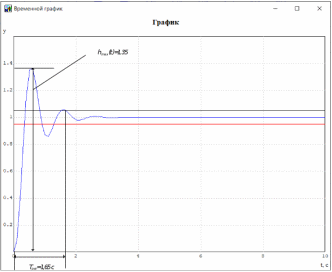 Рис.9.2. Переходная характеристика для оптимизации по среднеквадратичной ошибке Рис.9.2. Переходная характеристика для оптимизации по среднеквадратичной ошибкеПри выполнении оптимизации были получены следующие результаты(Рис.9.3). 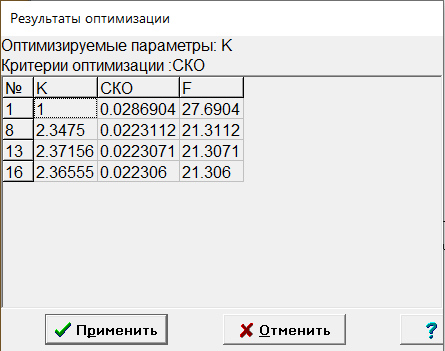 Рис.9.3. Результаты оптимизации В результате оптимизации параметра Kу получили Kу = 2.36555. Характеристики переходного процесса имеют следующие значения: Время регулирования: Tрег= 1,65c; Коэффициент перерегулирования: = 35%. 9.3 Оптимизация по критерию коэффициент перерегулирования Оптимизация проводилась по схеме, показанной на рис.9.4. 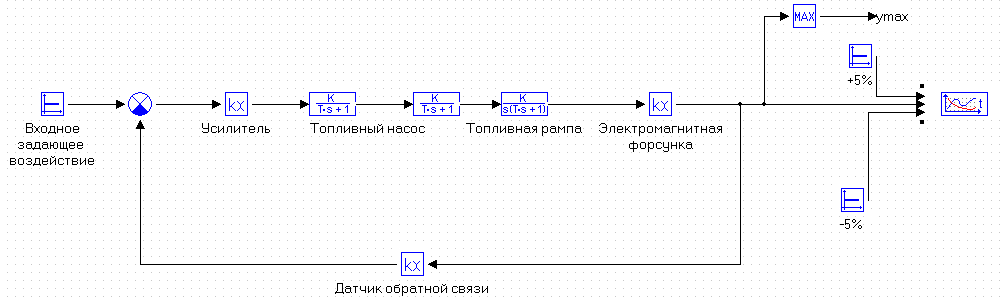 Рис.9.4. Схема моделирования для оптимизации по критерию «перерегулирование» Цель оптимизации нахождение минимального значения коэффициента перерегулирования. Коэффициент усиления Kу изменяем в пределах от 0,1 до 16,71. Оптимизация велась с интервалом неопределенных параметров = 0,01. 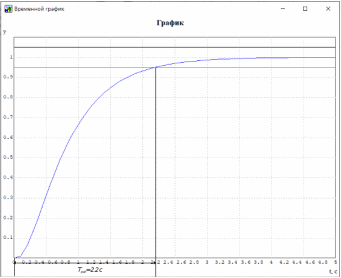 Рис.9.5. Переходная характеристика для оптимизации по коэффициенту перерегулирования При выполнении оптимизации были получены следующие результаты(Рис.9.6): 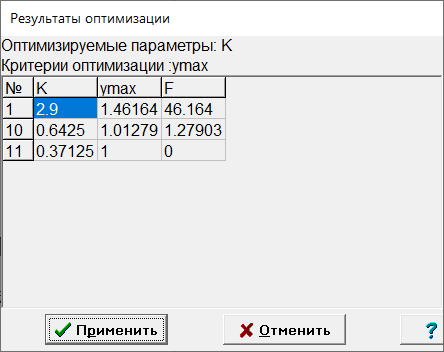 Рис.9.6. Результаты оптимизации по коэффициенту перерегулирования Коэффициент усиления: Kр = 0.37125; Время регулирования: Tрег= 2.2 с; Коэффициент перерегулирования: = 0%. 9.4. Оптимизация по критерию минимум времени регулирования Цель оптимизации нахождение минимального значения времени регулирования. Оптимизация проводилась по следующей схеме, показанной на рис.9.7. 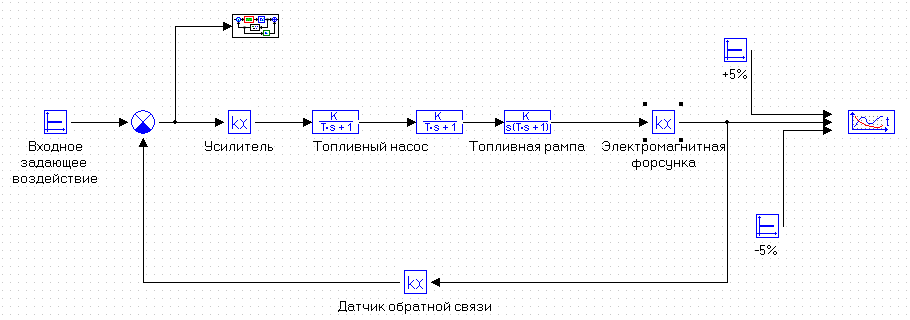 Рис.9.7. Схема моделирования для оптимизации по времени регулирования Принцип действия схемы субмодели: На средний (логический) входной порт (величина «трубки») подается модуль сигнала рассогласования. Если этот сигнал больше уставки (5%), то на выход подается сигнал с 3-его (нижнего) входного порта, т.е. текущее модельное время. Если управляющий сигнал (на среднем входном порту) меньше уставки, то на выход передается сигнал с первого (верхнего) входного порта, т.е. тот же сигнал, но задержанный на один шаг интегрирования. Задержку на один шаг интегрирования осуществляет типовой блок с подписью «Время переходного процесса» (типовой блок «Задержка на шаг интегрирования» из библиотеки «Дискретные звенья»). 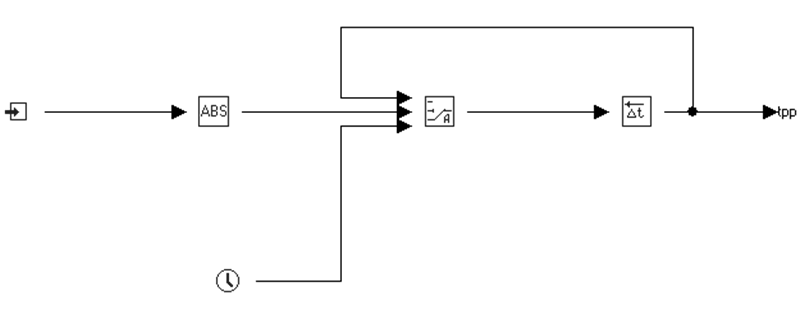 Рис.9.8. Схема субмодели 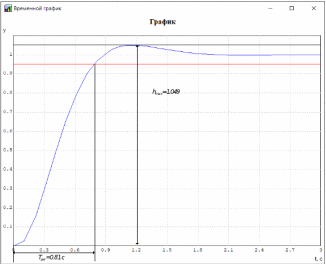 Рис.9.9. Переходная характеристика для оптимизации по времени регулирования При выполнении оптимизации были получены следующие результаты(Рис.9.10): 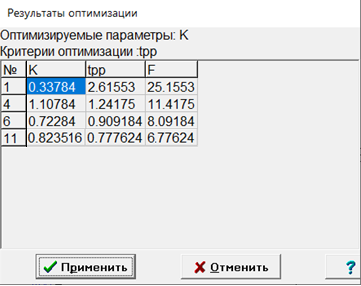 Рис.9.10. Результаты оптимизации по критерию «минимум времени регулирования» Коэффициент усиления Kу = 0,82351; Время регулирования: Tрег= 0,81c; Коэффициент перерегулирования: = 4.9%. 9.5 Оптимизация по суперкритерию Задача оптимизации – многофункциональная задача, т.к. имеет более одного параметра, претендующего на роль критерия оптимальности. Используем аддитивный суперкритерий, объединяющий все выходные параметры (частные критерии) в одну целевую функцию, представляющую собой сумму частных критериев: 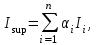 где 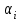 - относительный вклад частных критериев в суперкритерий; - относительный вклад частных критериев в суперкритерий;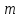 - число выходных параметров. - число выходных параметров.Для нашего случая аддитивный критерий будет выглядеть следующим образом: 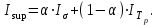 где α – весовой коэффициент. Оптимизация проводилась по следующей схеме: 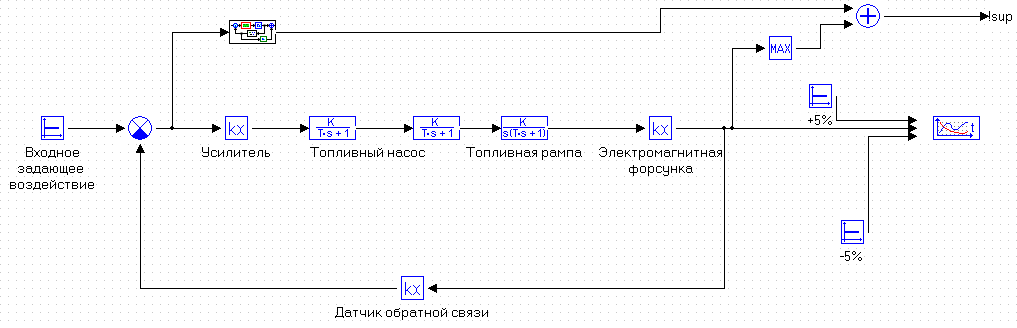 Рис.9.11. Схема моделирования системы для оптимизации по «суперкритерию» При оптимизации по суперкритерию проводятся те же вычисления, что и для других методов, при каждом значении α (от 0 до 1, шаг 0,2). 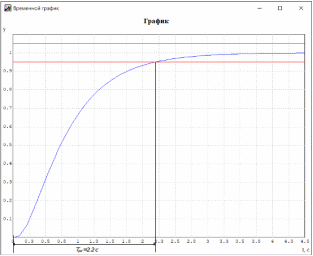 Рис.9.12. Переходная характеристика для оптимизации по суперкритерию при =0 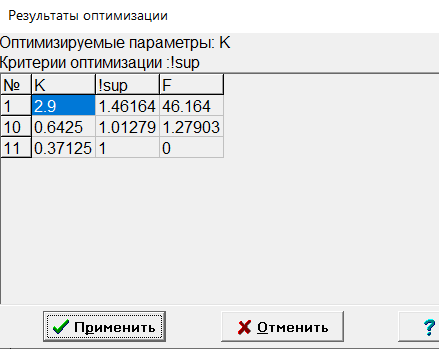 Рис.9.13. Результат оптимизации при =0 Время регулирования: Tрег= 2.2 с; Коэффициент перерегулирования: = 0%; 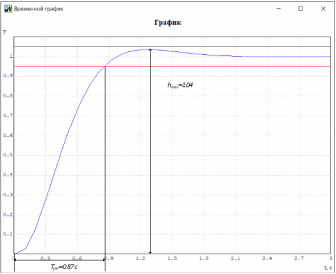 Рис.9.14. Переходная характеристика для оптимизации по суперкритерию при =0.2 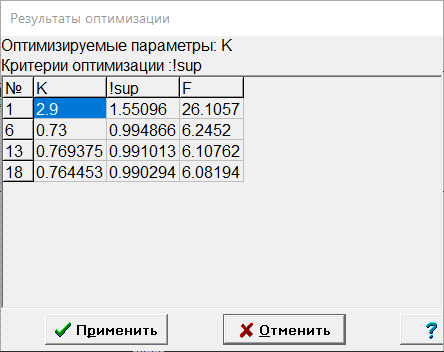 Рис.9.15. Результат оптимизации при =0.2 Время регулирования: Tрег= 0,87c; Коэффициент перерегулирования: = 4%; 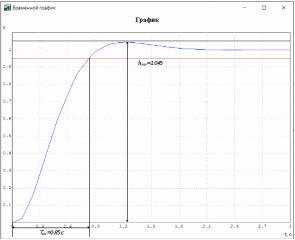 Рис.9.16. Переходная характеристика для оптимизации по суперкритерию при =0.4 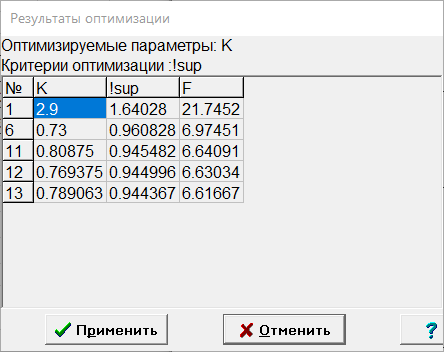 Рис.9.17. Результат оптимизации при =0.4 Время регулирования: Tрег= 0,85c; Коэффициент перерегулирования: = 4%; 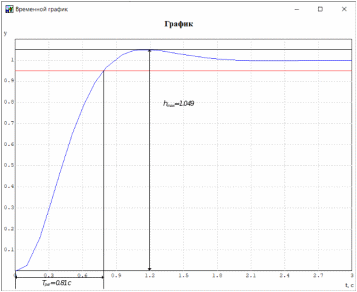 Рис.9.18. Переходная характеристика для оптимизации по суперкритерию при =0.6 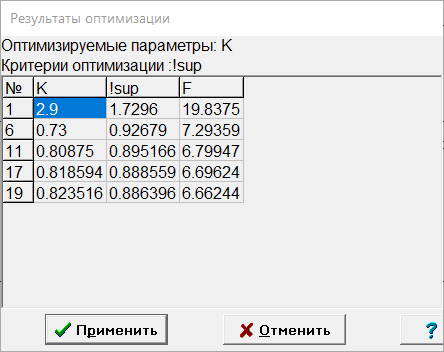 Рис.9.19. Результат оптимизации при =0.6 Время регулирования: Tрег= 0,81c; Коэффициент перерегулирования: = 4.9%; 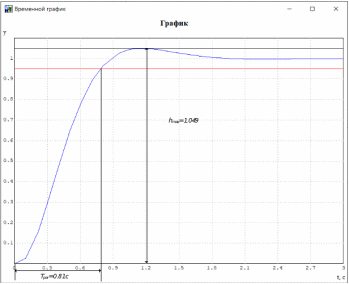 Рис.9.20. Переходная характеристика для оптимизации по суперкритерию при =0.8 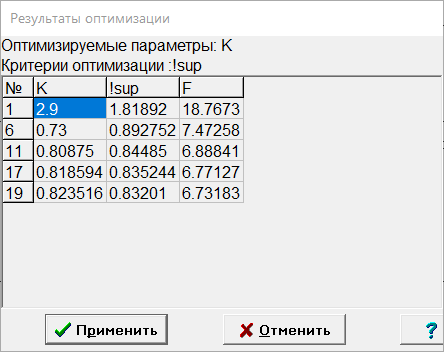 Рис.9.21. Результат оптимизации при =0.8 Время регулирования: Tрег= 0,81c; Коэффициент перерегулирования: =4.9%; 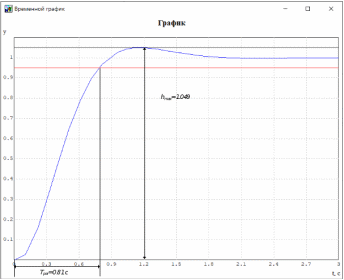 Рис.9.22. Переходная характеристика для оптимизации по суперкритерию при =1 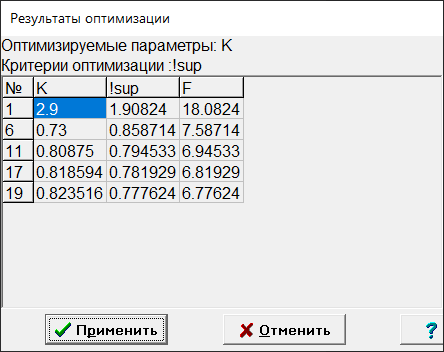 Рис.9.23. Результат оптимизации при =1 Время регулирования: Tрег= 0,81c; Коэффициент перерегулирования: =4.9%; 9.6 Построение множества Парето Строим график зависимости коэффициента перерегулирования (, %) от времени регулирования (tрег, с): исходной системы; по среднеквадратической ошибке; по перерегулированию; по времени регулирования; по суперкритерию (подставляя в уравнение 1 разные значения от 0 до 1 с интервалом 0,2). Таблица 1
Получаем точки, плавно соединив которые, строим некую интерполяционную кривую (рис. 50). Множество точек этой кривой называется областью компромиссов или областью (множеством) Парето. 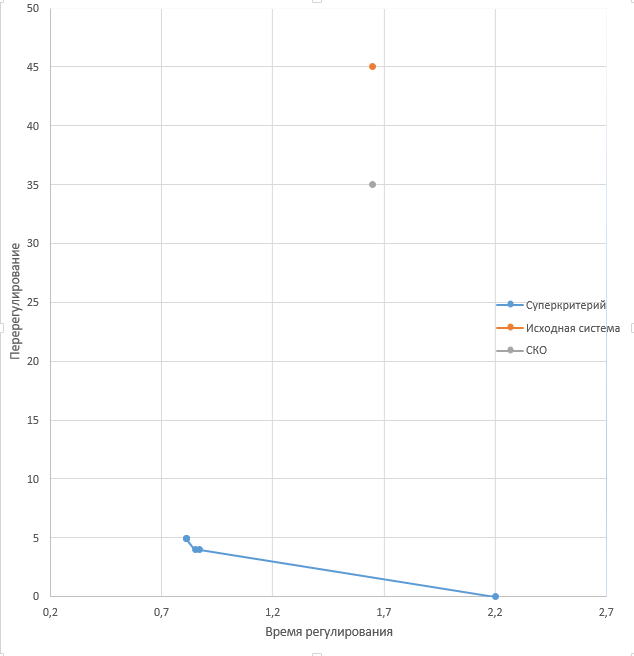 Рис.9.24. Множество Парето 10.ВыводыВ процессе проделанной работы по исследованию системы подачи топлива ДВС, проведена многокритериальная параметрическая оптимизация. Для исследования использовались критерии: среднеквадратическая ошибка (СКО); перерегулирование; время регулирования; суперкритерий. Таблица 2
Таким образом, не меняя исходной системы, можно добиться разных результатов, в зависимости от того, какая цель преследуется при параметрической оптимизации. Но при этом можно выделить наиболее оптимальное значения, в котором минимальное время регулирования и перерегулирования. Наиболее оптимальное значение получаем при K = 0,824, где 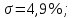 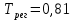 . .11. 3D-моделирование элементов СУ Рис.11.1. Топливный насос  Рис.11.2 Топливная форсунка  Рис.11.3 Лямбда-зонд 12. Список использованной литературы1.Проектирование автоматизированных систем: Курс лекций по дисциплине. Б.В. Кириличев. – М.: МГИУ, 2008. 2.Гришкевич А.И., Ломако Д.М., Автушко В.П. — Автомобили: Конструкция, конструирование и расчёт. Системы управления и ходовая часть. — Минск: Вышэйшая школа, 1987. — 200 с. 3. ГОСТ 10578-95 Насосы топливные дизелей 4. https://pro-sensys.com/info/articles/obzornye-stati/ustroystvo-i-printsip-raboty-toplivnoy-sistemy/ 5. https://www.autoezda.com/2014-07-01-16-12-30/%D1%83%D1%81%D1%82%D1%80%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%BE-%D1%82%D0%BE%D0%BF%D0%BB%D0%B8%D0%B2%D0%BD%D0%BE%D0%B9-%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B.html Москва 2021 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
