экзамен инф. Множества и операции над ними. Основные числовые множества. Множеством

• Название: Множества и операции над ними. Основные числовые множества. Множеством
• Анкор: экзамен инф
• Дата: 02.02.2022
• Размер: 1.75 Mb.
• Имя файла: ekzamen.docx
• Тип: Документы; #349497
• страница: 2 из 3

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность {x_n} имеет конечный предел, равный точной верней границе, sup {x_n} для неубывающей и точной нижней границе, inf {x_n} для невозрастающей последовательности.
Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности,  для неубывающей и минус бесконечности,  для невозрастающей последовательности.

Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.

e = 2.718281828459…

Способы определения числа e (формула):

1. Через предел:

Второй замечательный предел: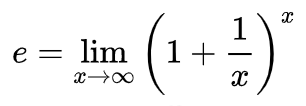



Альтернативный вариант (следует из формулы Муавра – Стирлинга):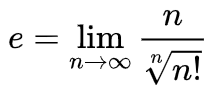

4. 
   Предел функции в точке. Односторонние пределы. Предел функции при x .
   

Число AA является пределом функции f(x)f(x) при x→∞x→∞, если последовательность ее значений будет сходиться к AA для любой бесконечно большой последовательности аргументов (отрицательной или положительной).

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Число  {\displaystyle A\in \mathbb {R} } называется правосторонним пределом (правым пределом, пределом справа) функции {\displaystyle f\left(x\right)}f(x) в точке {\displaystyle a}a, если для всякого положительного числа {\displaystyle \varepsilon }  отыщется отвечающее ему положительное число {\displaystyle \delta }  такое, что для всех точек {\displaystyle x}x из интервала {\displaystyle \left(a,a+\delta \right)}  справедливо неравенство {\displaystyle \left|f\left(x\right)-A\right|<\varepsilon } .

Число  {\displaystyle A\in \mathbb {R} } называется левосторонним пределом (левым пределом, пределом слева) функции {\displaystyle f\left(x\right)}f(x) в точке {\displaystyle a}a, если для всякого положительного числа {\displaystyle \varepsilon }  отыщется отвечающее ему положительное число {\displaystyle \delta }  такое, что для всех точек {\displaystyle x}x из интервала {\displaystyle \left(a,a+\delta \right)}  справедливо неравенство {\displaystyle \left|f\left(x\right)-A\right|<\varepsilon } .

При x→∞ предел функции f(x)) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).  

5. 
   Бесконечно большие и бесконечно малые функции. Основные теоремы о бесконечно больших и бесконечно малых функциях.
   

Определение бесконечно малой функции
Функция α(x) называется бесконечно малой при x стремящемся к x₀, если функция имеет предел при x → x₀, и он равен нулю:
.

Определение бесконечно большой функции
Функция f(x) называется бесконечно большой при x стремящемся к x₀, если функция имеет предел при x → x₀, и он равен бесконечности:
.

Теорема о произведении ограниченной функции на бесконечно малую

Произведение функции, ограниченной на некоторой проколотой окрестности точки x₀, на бесконечно малую, при x → x₀, является бесконечно малой функцией при x → x₀.

Теорема о сумме ограниченной функции и бесконечно большой

Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки x₀, и бесконечно большой функции, при x → x₀, является бесконечно большой функцией при x → x₀.

Теорема о произведении ограниченной снизу функции на бесконечно большую

Если функция , на некоторой проколотой окрестности точки , по абсолютной величине ограничена снизу положительным числом:
,
а функция  является бесконечно большой при x → x₀:
,
то их произведение является бесконечно большой функцией при x → x₀

Теорема о частном от деления ограниченной функции на бесконечно большую

Если функция f(x) является бесконечно большой при x → x₀, а функция g(x) – ограничена на некоторой проколотой окрестности точки x₀, то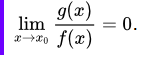

6. 
   Основные теоремы о пределах. Теоремы о предельном переходе.
   

ТЕОРЕМА 1

(О предельном переходе в равенстве). Если значения функций f(x) и g(x) в окрестности некоторой точки   равны, то и их пределы в этой точке совпадают:

ТЕОРЕМА 2

(О предельном переходе в неравенстве). Если в окрестности некоторой точки f(x) значения функции g(x)  не превосходят соответствующих значений функции f(x), то и предел функции  в этой точке не превосходит предела функции g(x)  в этой же точке:


ТЕОРЕМА 3

Предел константы равен этой константе:

ТЕОРЕМА 4

Если функция f(x), имеет предел, то он единственный.

ТЕОРЕМА 5

Если каждое слагаемое в сумме/разности функций имеет предел при  , то и сумма/разность имеет предел при  , причем предел суммы/разности равен сумме/разности пределов от каждой из функций:

ТЕОРЕМА 6

Если каждый из функций в конечном произведении имеет предел при  , то и произведение имеет предел при  , причем предел произведения равен произведению пределов:

ТЕОРЕМА 7

Постоянный множитель можно выносить за знак предела:

ТЕОРЕМА 8

Если функции f(x) и g(x)   имеют предел при  , причем  , то и их частное имеет предел при  , причем предел частного равен частному пределов:

ТЕОРЕМА 9

Если функция f(x имеет предел b при  , то ее можно представить как сумму числа b  и бесконечно малой функции при  .

ТЕОРЕМА 10

Если функцию f(x) можно представить как сумму некоторого числа b и некоторой бесконечно малой функции при  , то указанное число b является пределом функции f(x) при  .

7. 
   Первый замечательный предел. Второй замечательный предел.
   

Первый замечательный предел имеет вид  .

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.

Второй замечательный предел имеет вид  , где e = 2,718281828… – это иррациональное число.

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к  .

8. 
   Сравнение бесконечно малых и бесконечно больших функций. Таблица эквивалентных б.м.ф.
   

9. 
   Непрерывность функции в точке. Точки разрыва функции и их классификация.
   

Функция у = f(x) называется непрерывной в точке   , если существует предел функции в этой точке и он равен значению функции в этой точке

точками разрыва функции называются точки, в которых функция не обладает свойством непрерывности.

Классификация точек разрыва:

1. Точки разрыва первого рода (скачок) – точка   если фукнция имеет конечные но не равные односторонние пределы. (   )

Пример:     неравные односторонние пределы (разрыв первого рода).

2. Точки разрыва второго рода (бесконечный разрыв) - очка   если хотя бы один из односторонних пределов бесконечен или несуществует.

Примет: 
10 . Непрерывность функции в интервале и на отрезке. Свойства функций непрерывных на отрезке.

Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

При этом на концах отрезка или интервала необходима только односторонняя непрерывность.

войства функций, непрерывных на отрезке Свойство 1: (Первая теорема Вейерштрасса ). Функция, непрерывная

на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M≤ f(x)≤ M.

Свойство 2: Функция, непрерывная на отрезке [a, b], имеет на нем как наибольшее так и наименьшее значение.

Свойство 3: (теорема Коши). Функция, непрерывная на отрезке [a, b] такая, что f (a) = A, f (b) = B , то для любого значения C , заключенного между

A и B , существует такая точка ξ [a,b], что f (ξ) = C .

Иначе говоря, непрерывная на отрезке функция, принимающая какиелибо два значения, принимает и любое промежуточное.

Свойство 4: Если функция f(x) непрерывна в точке х=х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.

Свойство 5: (теорема Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, в которой функция обращается в нуль.

Т.е. если sign(f(a)) ≠ sign(f(b)), то x0 [a,b] : f(x0)=0.

Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого ε>0 существует δ >0 такое, что для любых точек х1 [a,b] и x2 [a,b] таких, что

	x1 − x2		<δ
верно неравенство			f(x2) – f(x1) < ε

Отличие равномерной непрерывности от “обычной” в том, что для любого ε существует свое δ , не зависящее от х, а при “обычной” непрерывности δ зависит от ε и х.

Свойство 6: (Теорема Кантора ). Функция, непрерывная на отрезке, равномерно непрерывна на нем.

Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором (конечном или бесконечном) интервале (a,b) , где

c = lim f (x),	d = lim f (x) , то и обратная ей функция х=g(y) так же
x→a+0	x→b−0

однозначна, монотонна и непрерывна на интервале с концами c и d .

11. Производная функции, ее механический смысл.
Произво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в

данной точке).

Механический смысл производной заключается в том, что скорость материальной точки равна производной закона пути движения этой точки:

12. Геометрический смысл производной. Уравнение касательной и нормали к графику функции.

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

Пусть функция y = f(x) в точке x0 имеет производную y(x0)=tga Тогда в точке M0(x0y0) существует касательная к графику этой функции, уравнение которой:



Пусть функция y = f(x) в точке x0 имеет производную y(x0)=tga Тогда в точке M0(x0y0) существует

Нормаль к графику функции уравнение которой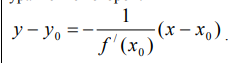

Если f(x0)=0 (то есть касательная горизонтальна), то нормаль вертикальна и имеет уравнение x=x0

13. Связь между дифференцируемостью и непрерывностью.

 Если функция   дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано.

14 Производная суммы, произведения, частного.

Производная суммы функций равна сумме производных каждой из функций:(u+v)′=u′+v′

Производная произведения равна произведению производной первого множителя на второй множитель плюс произведение первого множителя на производную второго множителя:

(uv)′=u′v+uv′

Производная частного равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя.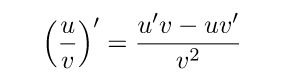



15. Производные сложной и обратной функций.

Теорема о производной обратной функции: Если функция у=f(x) имеет производную в т. Х₀, где f''(x₀)≠0, то функция х=f^-1(y) имеет также производную в этой точке, причем (f^-1(y₀))'= 

Теорема о производной сложной функции. Пусть функция u=u(x) имеет производную в точке х₀ , а функция y=f(u) имеет производную в точке u_o=u(x_o) . Тогда сложная функция y=f(u(x)) имеет производную в точке х₀, причем y’=f ’(u_o)•u’(x_o)

16 Производные основных элементарных функций.

К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций.


17. Логарифмическое дифференцирование. Дифференцирование функций заданных неявно и параметрически.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для нахождения производных степенных, рациональных и некоторых иррациональных функций.

Неявно заданная функция

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0).

Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.

Производная неявной функции выражается через аргумент х и функцию у.

<< Пример 21.1

Найти производную функции у, заданную уравнением х³+у³-3ху=0.

Решение: Функция у задана неявно. Дифференцируем по х равенство х³+у³-3ху=0. Из полученного соотношения

3х²+3у²· у'-3(1· у+х· у')=0

следует, что у²у'-ху'=у-х², т. е. у'=(у-х²)/(у²-х).

Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений



где t — вспомогательная переменная, называемая параметром.

Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции



Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем



Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

18. Дифференциал функции. Свойства дифференциала

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.

Дифференциал функции обладает свойствами, аналогичными свойствам производной.

1. 
   Дифференциал постоянной равен нулю:
   dc = 0, с = const.
   
2. 
   Дифференциал суммы дифференцируемых функцийравен сумме дифференциалов слагаемых:
   

d(u+v)=du + dv

Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны

d(u+c) = du (c= const).

3Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:

d(uv) = udv + vdu.

Следствие. Постоянный множитель можно выносить за знак дифференциала

d(cu) = cdu (с = const).

4Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой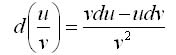



5Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

19. Производные и дифференциалы высших порядков. Формула Лейбница.







Дифференциалом 2ого порядка называют d(dy)=d²y=y’’(dx)².

Дифференциалом n-ого порядка dⁿy=d(d^n-1y)=y⁽ⁿ⁾(dx)ⁿ. Отсюда:

y⁽ⁿ⁾⁼ 

20. Теоремы Ролля, Лагранжа, Коши.

Теорема 1. (Теорема Ролля) Пусть функция   непрерывна на отрезке   , имеет производную   на интервале   и при этом   . Тогда существует точка   , в которой выполнено условие   .

Доказательство. Функция   непрерывна на отрезке   и, следовательно, достигает на этом отрезке свое наибольшее и наименьшее значения. Если эти значения совпадают, то функция равна константе, и ее производная равна 0 в каждой точке интервала   . Если же наибольшее и наименьшее значения функции не совпадают, то хотя бы одно из них не совпадает со значением функции на границах отрезка. Пусть в точке   достигается наибольшее или наименьшее значение функции на отрезке   . Тогда эта точка   является точкой экстремума и в этой точке по теореме Ферма производная равна 0. Теорема доказана.

Теорема 2. (Теорема Лагранжа) Пусть функция   непрерывна на отрезке   и имеет производную   на интервале   . Тогда существует точка   , в которой выполнено условие   , (1)

Формула (1) называется формулой Лагранжа. Иногда ее записывают в виде   и называют формулой конечных приращений Лагранжа.

Теорема 3. (Теорема Коши) Пусть функции   и   непрерывны на отрезке   , имеют производные   ,   на интервале   и при этом   при   . Тогда существует точка   , в которой выполнено условие   (2).

Формула (2) называется формулой Коши.

Доказательство. Заметим, что теорема Лагранжа является частным случаем теоремы Коши, если в качестве функции   взять функцию   . Для доказательства теоремы Коши рассмотрим вспомогательную функцию   . Заметим, что функция   непрерывна на отрезке   и имеет производную на интервале   , при этом   . Итак, для функции   выполнены все условия теоремы Ролля. Отсюда существует точка   , в которой выполнено условие   . Следовательно,   , что и равносильно условию (2). Теоремы Коши и Лагранжа доказаны.

21. Правило Лопиталя.

Правило Лопиталя. Предел отношения бесконечно малых или бесконечно больших величин равен пределу отношению производных, если предел отношения производных существует.

22. Формула Тейлора.



23 Формула Тейлора для основных элементарных функций.



24 Монотонность функции, условия монотонности.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.



25 Точки экстремума, необходимый признак экстремума.

Точки, в которых функция достигает максимума или минимума, называются точками экстремума функции, а значения функции в этих точках называют экстремальными.

Точка   называется точкой максимума (maximum) функции   , если значение функции в этой точке больше её значений во всех точках некоторого интервала, содержащего точку   , т.е.   для любого   (   — мало по величине).

   Точка   называется точкой минимума (minimum) функции   , если значение функции в этой точке меньше её значений во всех точках некоторого интервала, содержащего точку   , т.е.   .

Необходимый признак экстремума. Если дифференцируемая функция достигает в некоторой точке экстремума, то её производная в этой точке равна нулю или не существует

26 Достаточные признаки экстремума.

  Теорема (первый достаточный признак экстремума). Если x₀ - критическая точка функции f (х) и в некоторой окрестности этой точки, слева и справа от нее, производная имеет противоположные знаки, то   является экстремумом функции, причем:

    1) максимумом, если   при   и   при  ;

    2) минимумом, если   при   и   при  .

 Теорема. (Второй достаточный признак экстремума). Если функция f (х) дважды дифференцируема в окрестности точки x₀,   непрерывна в точке x₀ и в точке x₀ выполняются условия:  ,   , то в этой точке функция имеет экстремум, причем максимум, если  , и минимум, если  .

27 Выпуклость и вогнутость графика. Точки перегиба.

Определение 1

Дифференцируемая функция является выпуклой по направлению вниз на некотором интервале в том случае, когда ее график располагается не ниже касательной к нему в любой точке этого интервала.

Определение 2

Дифференцируемая функция является выпуклой по направлению вверх на некотором интервале в том случае, если график данной функции располагается не выше касательной к нему в любой точке этого интервала.

Определение 3

Точка перегиба функции – это точка M(x0; f(x0))M(x0; f(x0)), в которой существует касательная к графику функции, при условии существования производной в окрестности точки x0x0 , где с левой и правой стороны график функции принимает разные направления выпуклости.

28 Асимптоты графика. Схема полного исследования функции.

Асимптота -- это такая прямая, к которой график заданной функции приближается сколько угодно близко, но не пересекает ее. Среди асимптот выделяют следующие виды: вертикальная асимптота (параллельна оси ОY); горизонтальная асимптота (параллельна оси ОХ); наклонная асимптота (расположена под углом к осям координат). Отметим, что асимптоты на графике функции изображаются пунктирной линией.


29. Функции нескольких переменных. Основные понятия.