экзамен инф. Множества и операции над ними. Основные числовые множества. Множеством
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
1. Определение функции нескольких переменныхЕсли каждой паре (x, y) значений двух переменных x, y из некоторого множества D соответствует одно определенное значение переменной z, то говорят, что z – функция двух переменных x, y, определенная в области D. Множество Dназывается областью определения функции Z. Символически функция двух переменных записывается в виде равенства z = f(x, y), в котором f обозначает знак соответствия. Геометрически область определения D представляет собой некоторую часть плоскости Oxy, ограниченную линиями, которые могут принадлежать или не принадлежать области. Если функция задана формулой и область D её определения не указана, то считается, что D есть множество всех значений переменных, для которых эта формула имеет смысл. 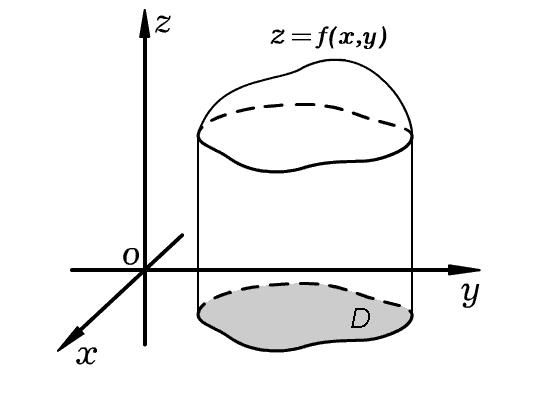 Вообще, величина z называется функцией переменных x1, x2, ..., xn, если каждой совокупности (x1, x2, ..., xn) переменных x1, x2, ..., xn из некоторого множества Dсоответствует определенное значение y, что символически записывается в виде z = f(x1, x2, ..., xn). Множество Dназывается областью определения функции y. Для каждой пары (x,y) из области определения функции z = f(x, y) можно построить точку M(x, y, z), где z = f(x, y). Множество всех таких точек называется графиком функции z = f(x, y). Обычно это некоторая поверхность. 2. Предел и непрерывность функции нескольких переменныхОкрестностью точки на плоскости называется любой круг с центром в этой точке, а окрестностью точки в пространстве – любой шар с центром в этой точке. На функции многих переменных переносятся такие понятия, как предел, непрерывность и т.п. Функция двух переменных z = f(x, y) называется непрерывной в точке M0(x0; y0), если Например, функция Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. 3. Частные производные и дифференциалыРассмотрим функцию z = f(x, y), определенную в точке M(x; y) и некоторой ее окрестности. Если переменной x придать некоторое приращение Δx, а y оставить постоянной, то функция z = f(x, y) получит приращение Δxz = f(x + Δx, y) - f(x, y), называемое частным приращением функции z по переменной x. Аналогично, Δyz = f(x, y + Δy) - f(x, y) называют частным приращением функции z по переменной y. Пределы если они существуют, называются частными производными функции z = f(x, y) по переменным xи yсоответственно. Частная производная Частная производная Все правила и формулы дифференцирования функций одной переменной применимы для нахождения частных производных функции любого числа переменных. Полным приращением функции z = f(x, y) называется разность Главная часть полного приращения функции z = f(x, y), линейно зависящая от приращений независимых переменных Δx и Δy, называется полным дифференциалом и обозначается dz. Если функция имеет непрерывные частные производные, то где dx = Δx, dy = Δy – приращения независимых переменных, называемые их дифференциалами. С точностью до бесконечно малых величин высшего порядка относительно Δx и Δy верно равенство Δz ≈ dz. Последнее применяется для нахождения приближенного значения функции в точке: 30. Предел функции нескольких переменных; непрерывность. Число НЕПРЕРЫВНОСТЬ. (continuity) Отсутствие внезапных скачков функции. Функция у=f(x) является непрерывной, если при изменении значения х на сколь угодно малую величину не происходит внезапных изменений значения у. Некоторые функции непрерывны при всех значениях х, 31 Частные производные функции нескольких переменных (ФНП).  32. Дифференцируемость ФНП, полный дифференциал.  ОПРЕДЕЛЕНИЕ. Если z = f(x,y) дифференцируема в точке M0(x0,y0), то линейная относительно Δx и Δy часть ее полного приращения в этой точке, т.е. называется полным дифференциалом функции z = f(x,y) в точке M0(x0,y0) и обозначается dz(M0) или df(x0,y0) 33 Производные сложной ФНП. Полная производная.  34. Инвариантность формы полного дифференциала Используя правила дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности, т.е. сохраняет один и тот же вид, независимо от того являются ли аргументы независимыми переменными или функциями независимых переменных.  35 Дифференцирование неявно заданной ФНП. Касательная плоскость и нормаль к поверхности. Определение 1: касательная плоскость к поверхности в точке Определение 2: нормаль к поверхности в точке  36 Частные производные и полные дифференциалы высших порядков. Определение 1. Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Теорема (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой. Дифференциалы высших порядков. Так как , 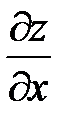 по предположению имеют непрерывные частные производные первого порядка, то от функции , в свою очередь, можно взять полный дифференциал по предположению имеют непрерывные частные производные первого порядка, то от функции , в свою очередь, можно взять полный дифференциал 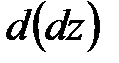 . Так получим полный дифференциал второго порядка (или, кратко, второй дифференциал), который обозначается . Так получим полный дифференциал второго порядка (или, кратко, второй дифференциал), который обозначается 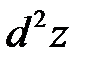 37 Экстремум ФНП. Необходимый признак экстремума ФНП. Формулировка достаточного признака экстремума функции двух переменных.   .  38. Условный экстремум. Метод множителей Лагранжа.   |
