Модель материала арматуры
 Скачать 355.74 Kb. Скачать 355.74 Kb.
|
 Содержание
Введение. Основой анализа напряженно-деформированного состояния (НДС) структурно-неоднородных физически нелинейных материалов, к которым относится железобетон, являются методы вычислительной механики. Математическая модель такого материала должна учитывать особенности деформирования его структурных компонентов (арматуры и бетона), а также их контактное взаимодействие (сцепление). Идентификацию параметров математической модели проводят на основе данных натурных экспериментов. Для арматуры и бетона достаточно проведения стандартных механических испытаний материалов. В свою очередь, известные экспериментальные схемы изучения сцепления арматуры с бетоном дают только косвенную информацию о характеристиках контакта и разрушении пограничной области. Поэтому для моделирования сцепления разрабатываются математические модели, упрощающие реальные процессы взаимодействия структурных компонентов.
Для описания предельного состояния арматуры и окружающего ее бетона использованы модели пластичности материала, основанные на классических критериях текучести Мизеса и Друкера Прагера. При моделировании нелинейных процессов, происходящих в зоне сцепления, предлагается выделять на границе с арматурой контактный слой (КС), параметры которого идентифицируются по экспериментальной кривой податливости арматуры при ее вытягивании из бетона. Такой подход не учитывает детальное распределение деформаций в зоне взаимодействия, однако позволяет рассматривать железобетон как сплошную неоднородную среду с идеальным контактом его структурных компонентов. Для тестирования предложенной модели железобетона рассмотрены прикладные задачи, в которых учет контактного взаимодействия арматуры с бетоном играет существенную роль при исследовании деформирования объектов. Это вытягивание упругопластической арматуры из бетона и изгиб армированной балки сложной геометрии. 1. Математическая модель железобетона. 1.1. Нелинейное деформирование бетона. Бетон является упругопластическим материалом, прочность которого на сжатие выше, чем на растяжение. Этот факт иллюстрирует диаграмма его деформирования, показанная на рис. 1 штриховой линией. Следовательно, для бетона необходимо выбирать критерии, учитывающие зависимость пластических деформаций от среднего напряжения. Подобные критерии можно разделить на две группы. К первой относятся критерии пластичности, которые имеют коническую форму поверхности текучести, например Друкера Прагера. Вторую группу составляют законы, соответствующие поверхностям более высокого порядка: параболический закон Друкера Прагера, нелинейный критерий Виллама Варнке. Последняя теория более точно описывает упругопластическую работу материала, однако для определения ее параметров требуются опытные данные, получение которых вызывает технические трудности. Например, для использования критерия Виллама Варнке требуется пять видов испытаний: осевое растяжение и сжатие, двухосное сжатие, а также значения прочности при двух различных видах напряженного состояния, соответствующие более высокому уровню гидростатического сжатия. 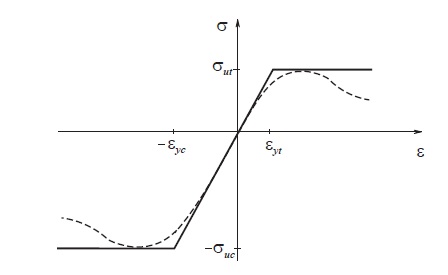 Рис. 1. Экспериментальные и модельные диаграммы деформирования бетона при растяжении и сжатии Параметры конических законов связаны с двумя характеристиками материала: предельными напряжениями при одноосном растяжении ��ut и сжатии ��uc, значения которых известны для всех стандартных классов бетона. Поэтому для описания НДС бетона выбрана функция текучести Друкера Прагера: Здесь ��1 первый инвариант тензора напряжений; ��2 второй инвариант девиатора напряжений: 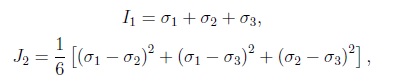 где , ���� , �� = 1, 2, 3, главные напряжения Параметры и �� и k в соотношении уравнений непосредственно связаны с ��ut и ��uc: 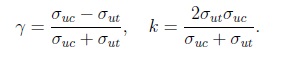 При постоянном предельном напряжении k в формуле текучести диаграмма деформирования бетона будет соответствовать диаграмме идеальной текучести, которая представлена сплошной линией на рис. 1. 1.2. Модель материала арматуры. В общем случае для армирования бетона применяется упругопластический материал, работу которого можно описать функцией: 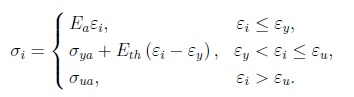 Здесь ����, ���� - интенсивность напряжений и деформаций; ���� - модуль упругости; ����ℎ - касательный модуль; ������, ������ - пределы текучести и прочности материала арматуры; ����, ���� - деформации, соответствующие пределу текучести и прочности.
критерия Мизеса: При наличии участка упрочнения на диаграмме, соответствующей функции, величина k переменна и зависит от интенсивности пластической деформации и в соответствии с формулой напряжения изменяется от ������ до ����. 1.3. Моделирование взаимодействия арматуры с бетоном. Нелинейные процессы, связанные с контактным взаимодействием арматуры с бетоном, оказывают влияние на довольно малую область. Поэтому при моделировании эту зону предлагается рассматривать как контактный слой (КС) из упругопластического материала, отличающегося от бетона механическими характеристиками. Впервые КС был использован в “технической теории сцепления”, разработанной М.М. Холмянским. Этот слой полагался бесконечно тонким, а условия по контакту описывались нормальным законом сцепления зависимостью касательных напряжений от взаимных продольных смещений бетона и арматуры g: 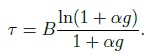 Эта теория упрощает реальное распределение деформаций в конструкции. Однако зависимость взаимного смещения арматуры и бетона от напряжений согласно этой теории хорошо соответствует экспериментальным данным при вытягивании арматуры из бетона (рис. 2, а): 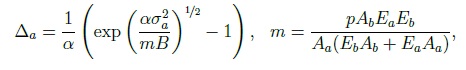 Где ���� и ���� - площадь сечения арматуры и бетона; р - периметр сечения арматурного стержня, ���� - модуль упругости бетона. Это позволило значения �� и B считать параметрами сцепления, которые связаны с характеристиками бетона и арматуры, и определять их аппроксимацией экспериментальных данных зависимостью. Следует отметить, что это соотношение получено для образцов, у которых длина заделки L больше длины зоны, где ������ - напряжения падают до нуля (рис. 2, б). На участке, расположенном выше этой зоны, взаимные смещения арматуры относительно бетона отсутствуют. На рис. 3 штрихпунктирной линией представлен график нормального закона сцепления, который подобен реальным диаграммам растяжения и сжатия бетона (см. рис. 1). Поэтому предложено контактный слой моделировать упругопластическим материалом. Численный анализ НДС модели железобетона с контактным слоем по расчетной схеме вытягивания (рис. 2, а) показал, что его элементы находятся в состоянии, 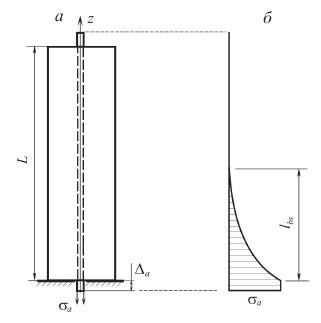 Рис. 2. Схема вытягивания арматуры из бетона (a); эпюра нормальных напряжений в арматурном стержне (б) 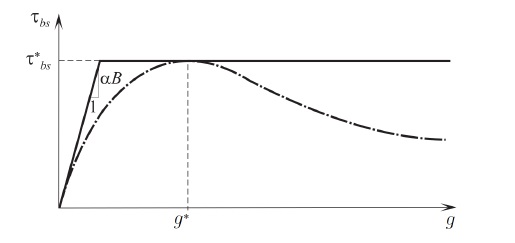 Рис. 3. График нормального закона сцепления и диаграмма условий контакта арматуры с бетоном близком к чистому сдвигу, при котором ��1 = 0, а выражение текучести приобретает вид критерия Мизеса. В этом случае модельные условия по контакту арматуры с бетоном можно представить в виде двухлинейной диаграммы, изображенной на рис. 3 сплошной ли-нией. Механические характеристики модели контактного слоя свяжем с параметрами сцепления и B. Из формулы критерия Мизеса получим связь максимального касательного напряжения с напряжением, при котором начинается пластическое деформирование контактного слоя: Определим значение ������. Из формулы закона сцепления получим: 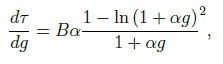 откуда выразим смещение ��*, соответствующее 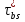 *, подставляя которое в формулу критерия Мизеса, определим *, подставляя которое в формулу критерия Мизеса, определим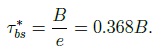 Учитывая соотношение пластического деформирования контактного слоя, получим характеристику контактного слоя Модуль упругости контактного слоя ������ соответствует линейному участку графика функции критерии Мизеса 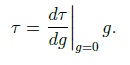 Из соотношения смещения получим 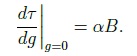 Из этих уравнений следует, что 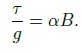 Смещение g определим как сдвиг по толщине слоя ������, считая, что сдвиговые деформации в основном сосредоточены в элементах контактного слоя: 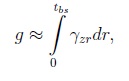 где z и r - координаты точки в цилиндрической системе. Интеграл ������ выразим через площадь эпюры по толщине КС где n - коэффициент наполнения эпюры; ��0 - упругая деформация сдвига на границе КС и арматуры. Касательные напряжения �� определим по закону Гука 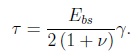 Из исходных уравнений получим соотношение, связывающее параметры сцепления �� и B с модулем упругости контактного слоя: Здесь коэффициент n зависит от характера разбиения контактного слоя на конечные элементы. 2. Практическое использование модели армированного бетона. Валидация предложенной математической модели проводилась на двух прикладных задачах: вытягивание профилированной арматуры из бетонного цилиндра и изгиб железобетонной балки сложной геометрии. Такие нелинейные задачи могут быть решены только методами вычислительной механики, среди которых следует выделить метод конечных элементов как наиболее разработанный и универсальный . При составлении системы уравнений МКЭ относительно приращений узловых перемещений учитывалась степень геометрической нелинейности моделей материалов.
Задача решалась пошаговым интегрированием линеаризованных уравнений МКЭ.
При относительно большом шаге численное решение может достаточно далеко уйти от истинного. Для того чтобы исправить эту ситуацию, применяются итерационные процедуры уточнения решения. В нашем случае используется стандартный метод Ньютона Рафсона, который хоть и трудоемок, так как требует вычисления и триангуляризации матрицы касательной жесткости на каждой итерации, но обладает наилучшей сходимостью. Для определения геометрических параметров конечных элементов были проведены численные эксперименты с вариацией их размеров. Установлено, что значительное влияние на результат решения оказывает размер 0 конечного элемента КС, расположенного на границе с арматурой. В результате определены рациональные размеры конечного элемента и толщина контактного слоя, а также коэффициент наполнения эпюры ������: Где ���� - номинальный диаметр арматуры, ���� - характерный размер бетонной обоймы. Параметры моделей определялись по исходным данным для арматуры, бетона и КС: постоянные пластичности �� и k - по формулам предельных напряжений, характеристики сцепления �� и B - аппроксимацией экспериментальных данных c использованием зависимости, напряжение пластического деформирования контактного слоя ������ - по формуле контактного слоя, модуль упругости КС ������ - по формуле упругости контактного слоя, геометрические параметры КС - по формулам конечного элемента. Во всех моделях арматура сложной геометрии заменялась на сплошной однородный цилиндр равной площади поперечного сечения. 2.1. Вытягивание профилированной арматуры из бетона. Профилированная арматура номинального диаметра 8 мм статически вытягивалась из бетонного цилиндра диаметром 152 мм и длиной 400 мм. По схеме, приведенной на рис. 2, проведены испытания для пяти подобных образцов, результаты которых представлены на рис. 4 светлыми точками. Параметры модели указаны в табл. 1. На рис. 4 сплошной линией приведены результаты численного моделирования. Можно отметить удовлетворительную сходимость расчета с экспериментальными данными при упругой и пластической деформациях арматуры. Таблица 1 - Параметры модели вытягивания профилированной арматуры из бетона
Примечание. Для арматуры коэффициент пластичности k изменяется в диапазоне 400 ≤ ≤ 600 МПа. 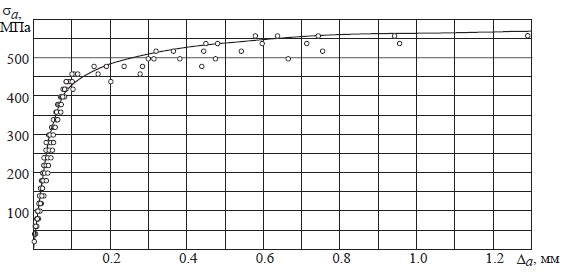 Рис. 4. - Результаты численного (кривая) и физического (светлые кружки) моделирования вытягивания арматуры 2.2. Изгиб железобетонной балки. Для проверки математической модели сцепления арматуры с бетоном, который испытывает неоднородное деформирование, были проведены исследования изгиба железобетонной балки, геометрия и схема нагружения которой показаны на рис. 5. Балка армирована тремя арматурными стержнями номинального диаметра 16 мм. В работе экспериментального определения дифференцированного закона сцепления стержневой арматуры с бетоном, представлены экспериментальные данные испытаний такого образца. Здесь методом тензометрирования были измерены деформации среднего стержня по длине заделки 300 мм. Экспериментальные результаты показаны на рис. 6 светлыми точками. Учитывая, что асимметрия заделки арматуры в бетон сказывается только при предельном состоянии балки, конечно-элементная модель построена для правой четверти образца из 25 306 восьмиузловых объемных конечных элементов. 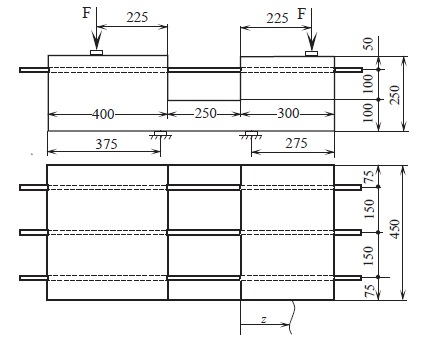 Рис. 5 -. Схема нагружения железобетонной балки 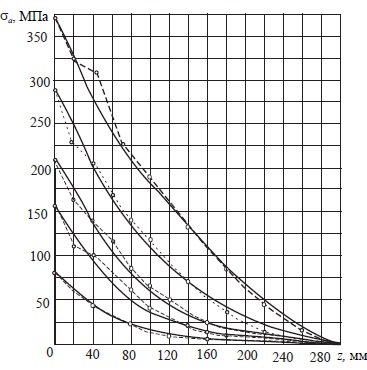 Рис. 6. - Распределение напряжений по длине заделки среднего арматурного стержня 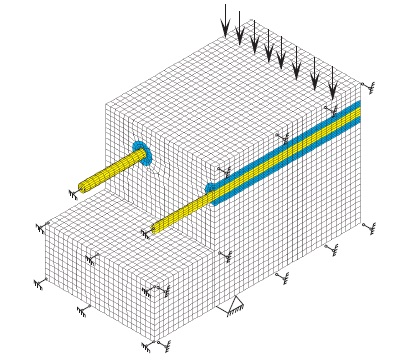 Рис. 7 - Конечно-элементная модель железобетонной балки Таблица 2 - Параметры модели изгиба балки
Сетка сгущалась в контактном слое, в направлении армирования выбрано равномерное распределение размеров элементов (рис. 7). Расчетные параметры модели представлены в табл. 2. На рис. 6 сплошной линией представлены результаты расчета напряжений в среднем арматурном стержне по длине его заделки 300 мм при разных уровнях нагружения. Видно, что расчетные графики соответствуют экспериментальным данным. Заключение. Разработана математическая модель нелинейного деформирования железобетона. Обоснован выбор критериев пластичности для арматуры, бетона и контактного слоя, введенного для учета нелинейных процессов, происходящих в области взаимодействия. Разработаны процедуры идентификации параметров материала КС, в которых используются данные испытаний вытягивания арматуры из бетона. Численная реализация модели для осесимметричного и пространственного объектов показала, что предложенные теоретические выводы хорошо воспроизводят деформирование реальных железобетонных конструкций и адекватно описывают взаимодействие арматуры с бетоном при длине заделки больше нелинейной зоны контактного взаимодействия. Список используемых источников.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
