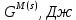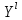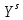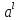ЛР1. +ЛР1_. Моделирование диаграмм состояния полупроводниковых систем с неограниченной растворимостью компонентов в жидкой и твердой фазах
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра микро- и наноэлектроники отчет по лабораторной работе №1 по дисциплине «ФХОТ изделий электроники и наноэлектроники» Тема: Моделирование диаграмм состояния полупроводниковых систем с неограниченной растворимостью компонентов в жидкой и твердой фазах
Санкт-Петербург 2020 Цель работы: Изучение фазовых равновесий в бинарных полупроводниковых системах с непрерывным твердым раствором методом компьютерного моделирования; расчет параметров межатомного взаимодействия; выбор моделей растворов, адекватно описывающих экспериментальную Т-х-проекцию диаграммы состояния. Экспериментальные результаты и исходные данные Система: GaSb-GaAs Таблица 0: Координаты точек линий ликвидуса и солидуса
Температуры плавления: 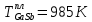 ; ; 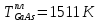 Энтальпии плавления: 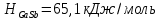 ; ; 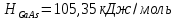 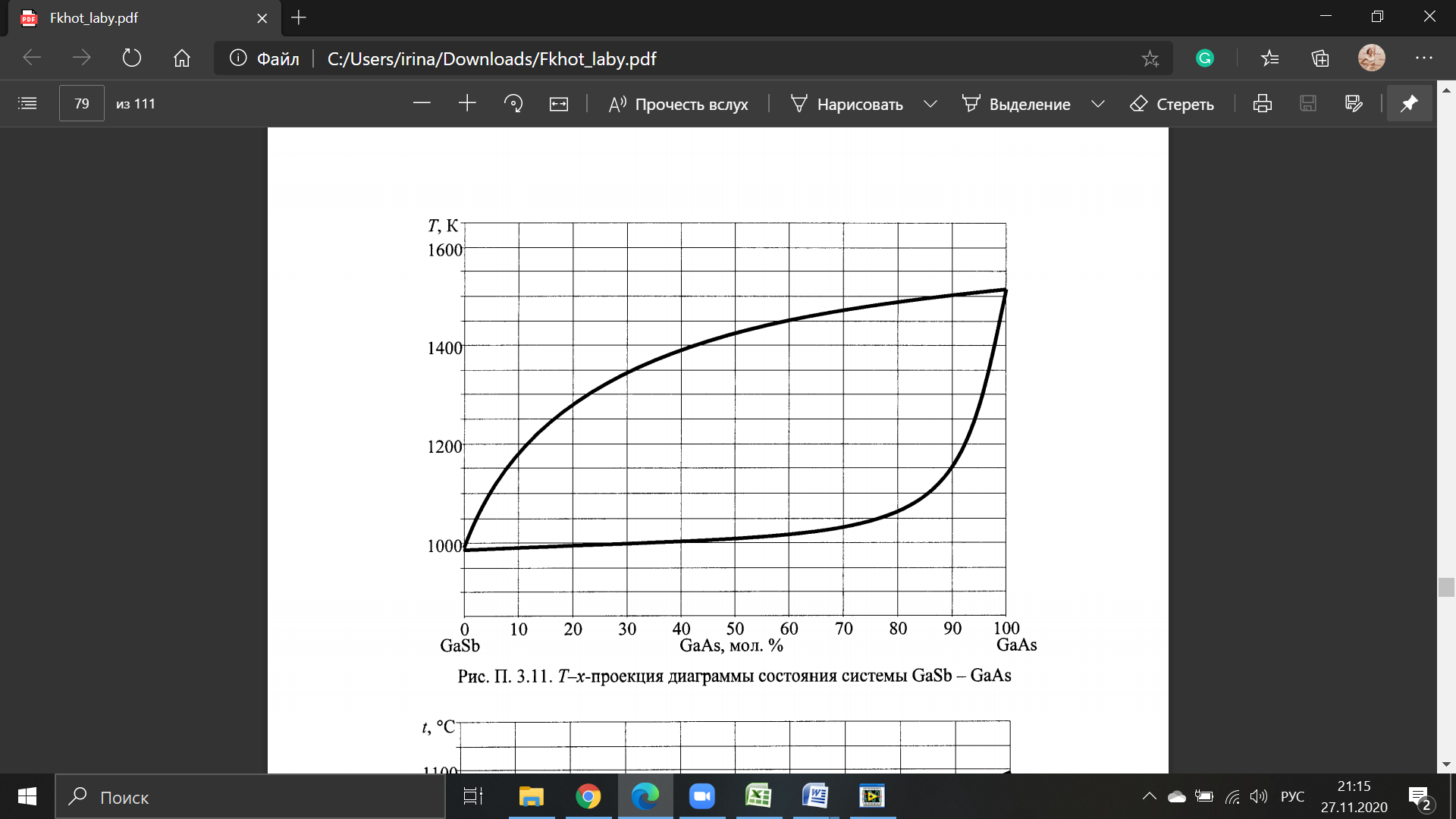 Рис.0 Т-х проекция диаграммы состояния системы GaSb-GaAs Обработка результатов эксперимента Приведем Т-х проекции диаграмм состояния (экспериментальной и теоретически рассчитанной), а также найденные значения параметров взаимодействия Wl opt и Ws opt: 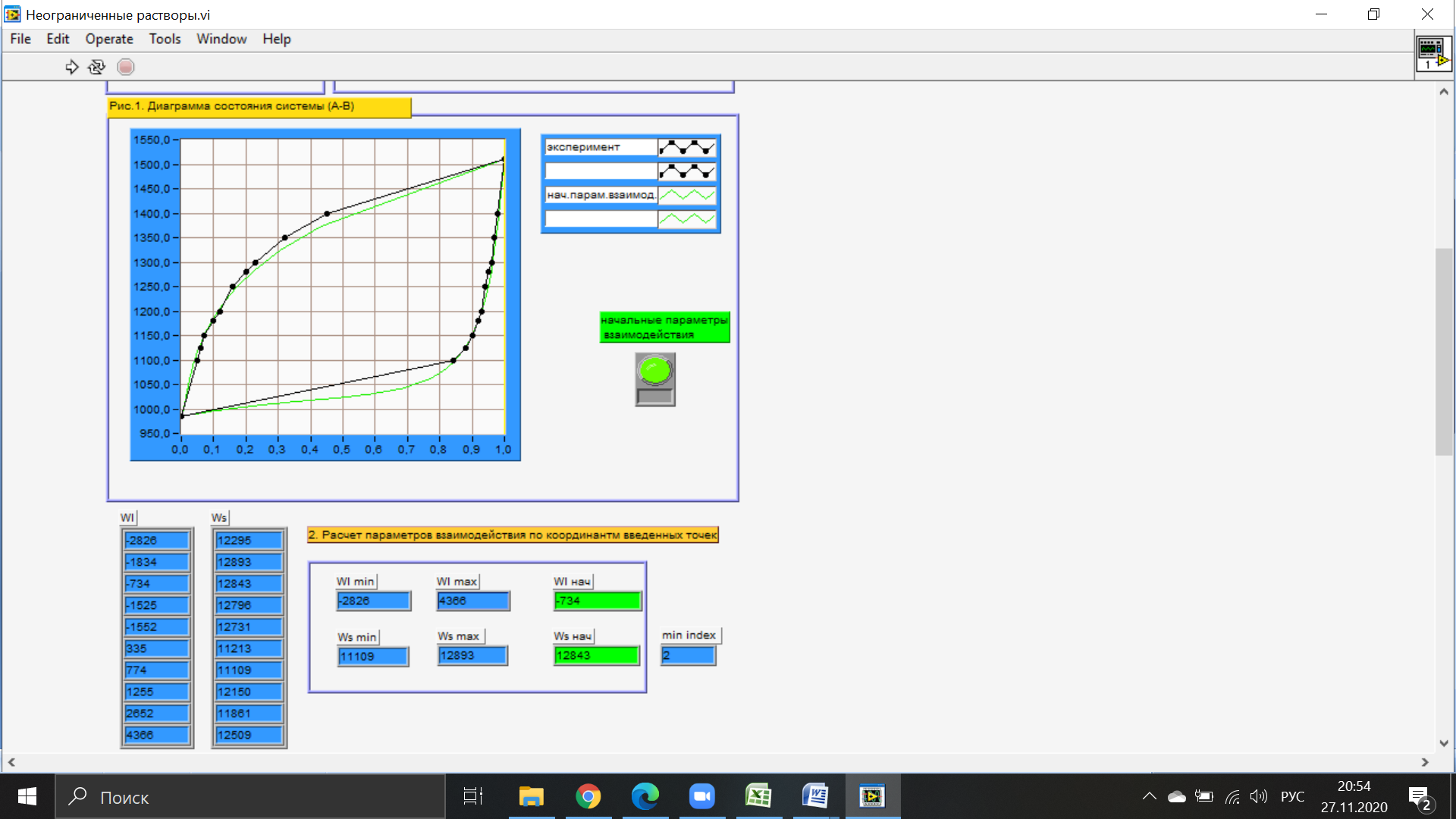 T, К X, мол. Рис.1.1 Т-х проекция диаграммы состояния системы GaSb-GaAs, построенная в среде LabView Был произведен поиск более точного приближения параметров взаимодействия к оптимальным, ими являются такие параметры взаимодействия, которые соответствуют минимуму СКО при операции сужения диапазона параметров взаимодействия. 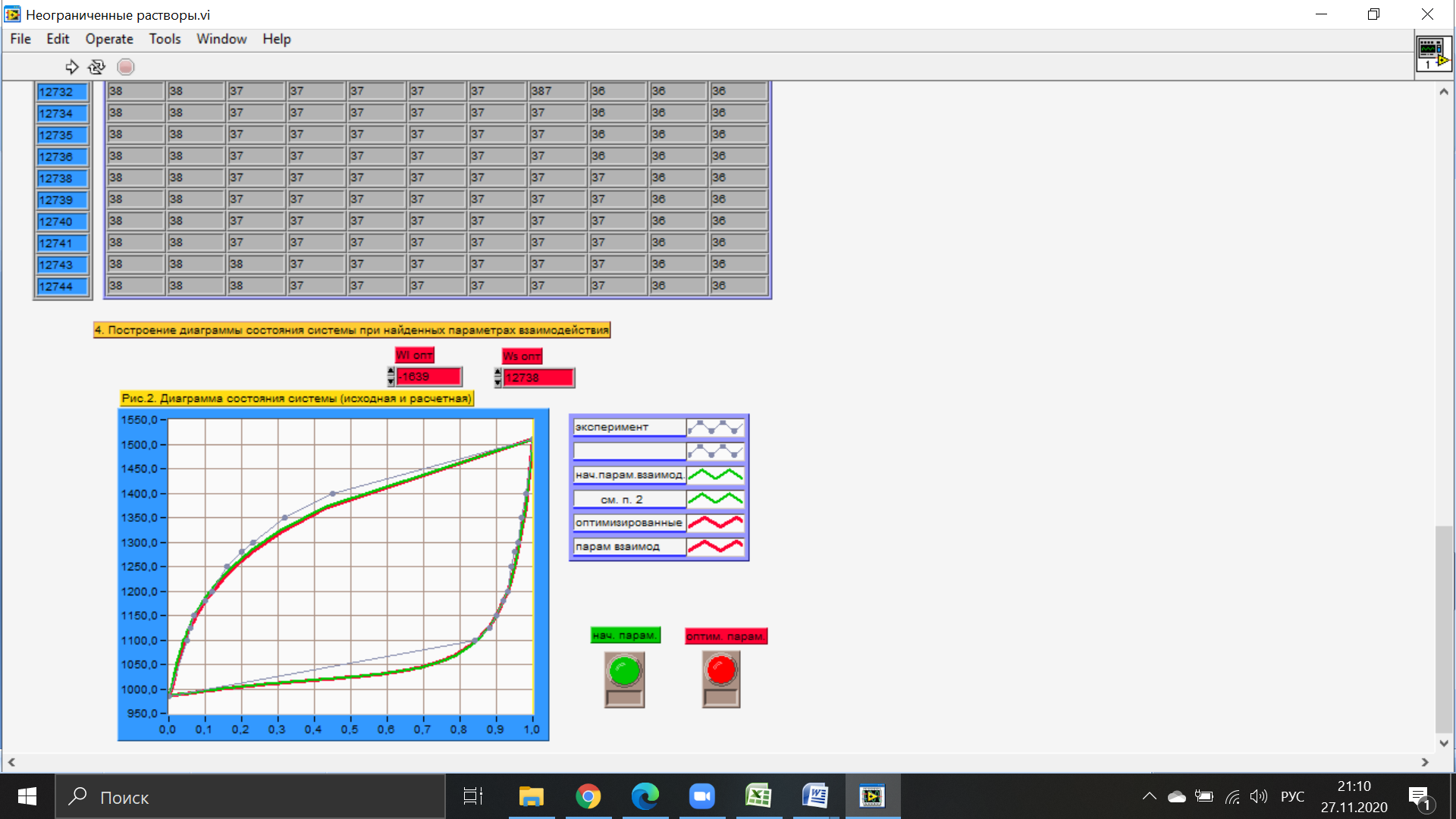 T, К X, мол. Рис.1.2 Т-х проекция диаграммы состояния системы GaSb-GaAs, при найденных параметрах взаимодействия Таким образом, найдены следующие оптимальные параметры межатомного взаимодействия в жидком (Wl) и твердом (Ws) растворах: 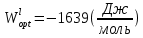 ; ; 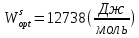 Приведем Т-х проекции диаграмм состояния, построенные в соответствии с п.11 методических указаний: 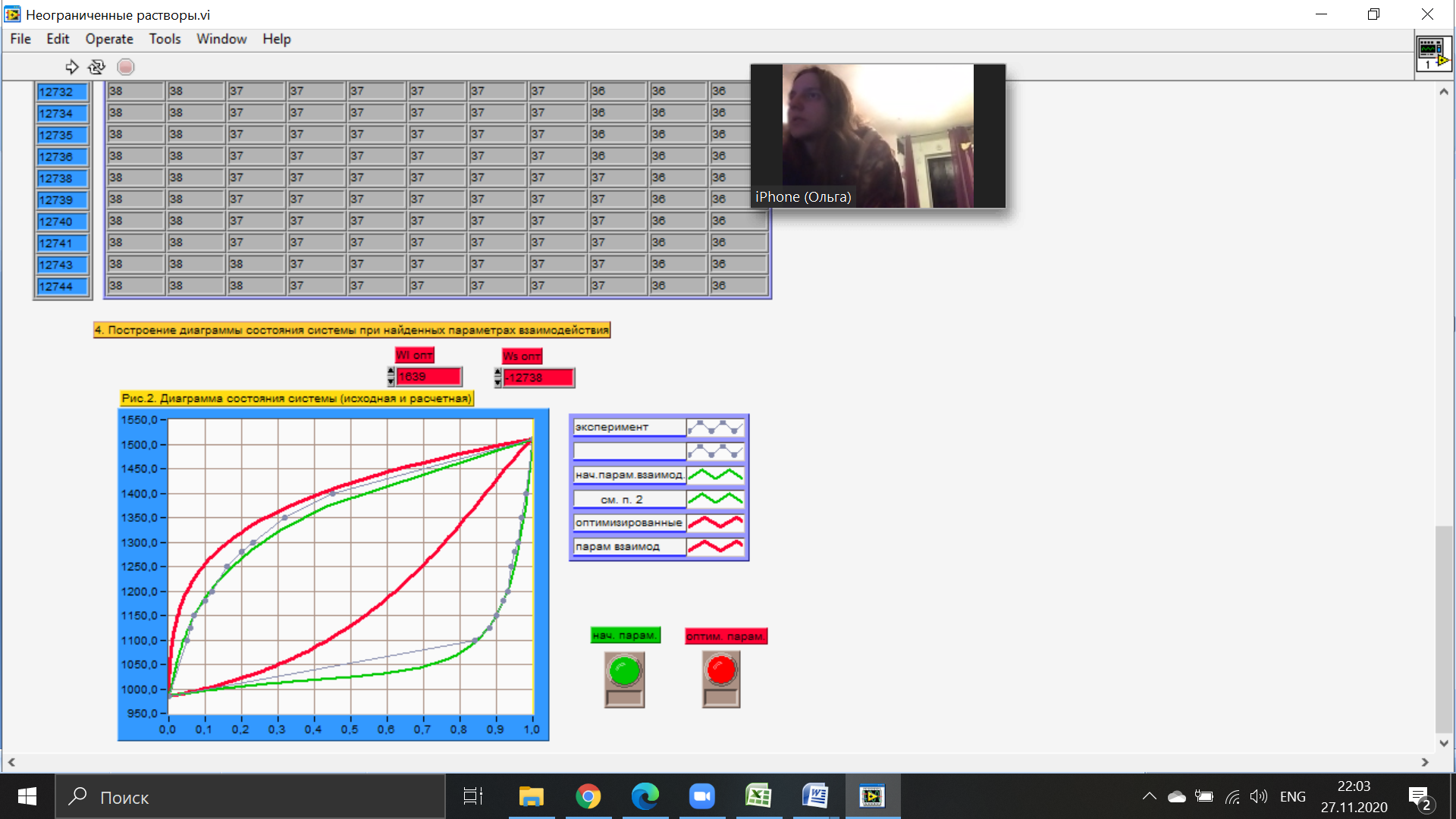 T, К X, мол. Рис.2.1 Т-х проекция диаграммы состояния системы GaSb-GaAs, при найденных параметрах взаимодействия, отличающихся по знаку При существенном изменении параметров Ws и Wl диаграмма состояния сильно отклоняется от теоретической кривой, что показывает правильность нахождения оптимальных параметров. 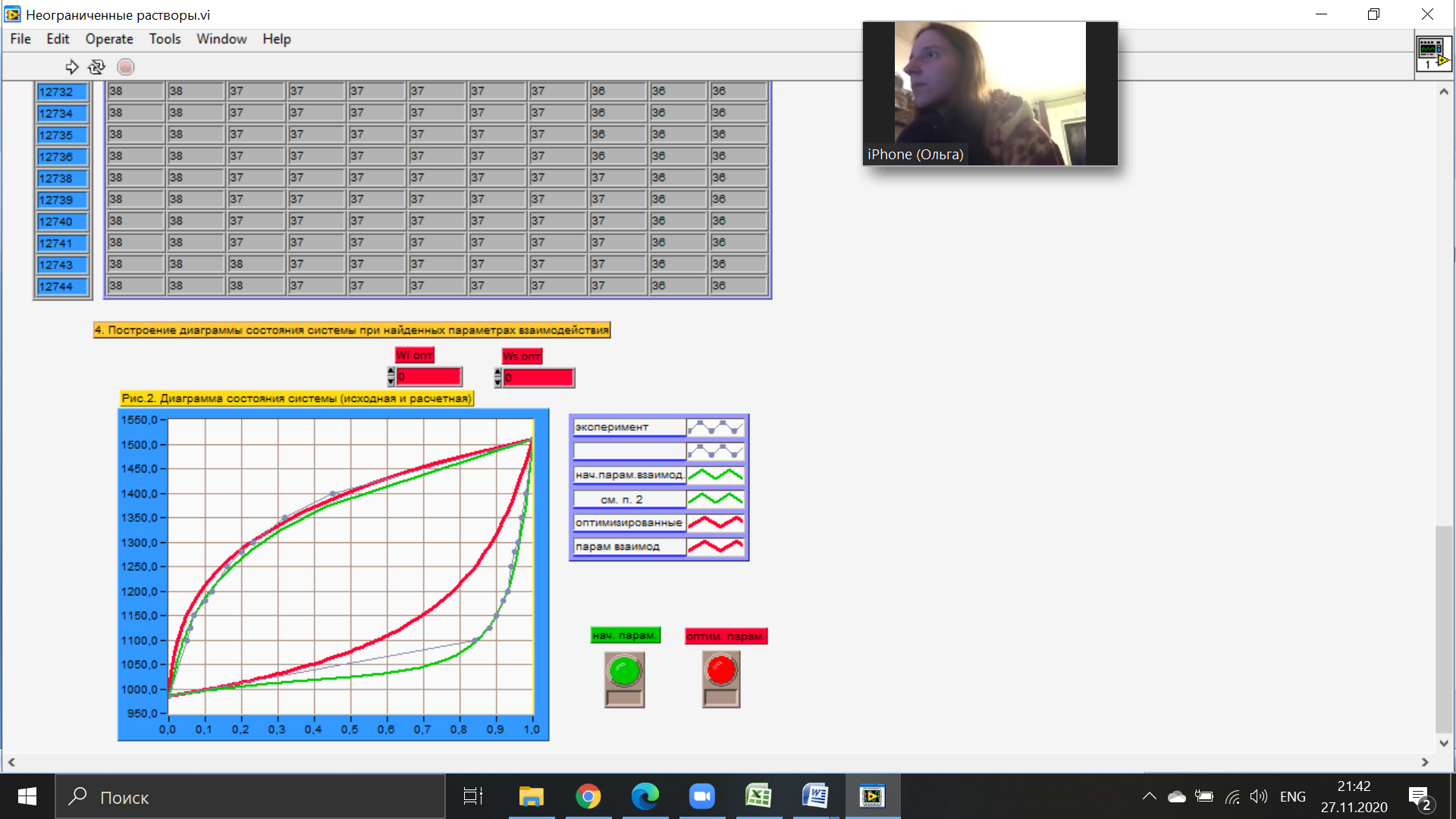 Рис.2.2 Т-х проекция диаграммы состояния системы GaSb-GaAs, при параметрах взаимодействия, равных нулю (модель идеального раствора) Расчет и построение концентрационных зависимостей термодинамических функций смешения 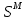 , , 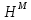 , , 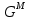 для твердого и жидкого растворов при для твердого и жидкого растворов при 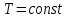 . .Пусть 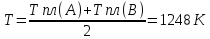 . .Расчетные формулы: 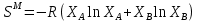 , ,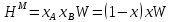 , ,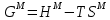 , ,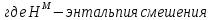 ; ; 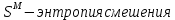 ; ; 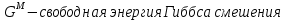 ; ; 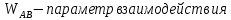 ; ; 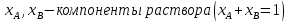 . .Пример расчета при 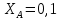 : : 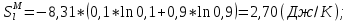 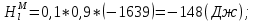 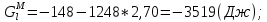 По данным таблиц 1-2 построены графики концентрационных зависимостей 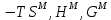 для жидкого и твердого растворов, которые приведены на рисунках 3.1 и 3.2. для жидкого и твердого растворов, которые приведены на рисунках 3.1 и 3.2.Таблица 1: Результаты расчета термодинамических функций смешения твердого р-ра
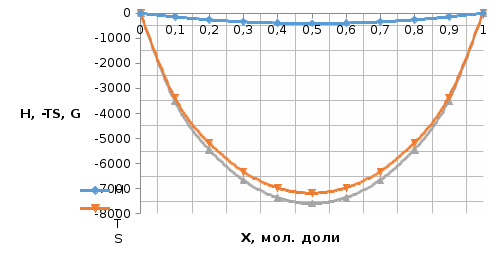 Рис.3.1 Графики концентрационных зависимостей 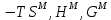 для твердого раствора для твердого раствораТаблица 2: Результаты расчета термодинамических функций смешения жидкого р-ра
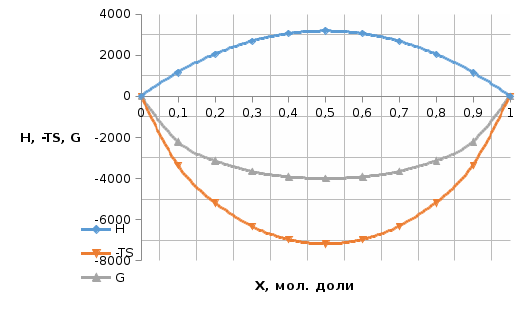 Рис.3.2 Графики концентрационных зависимостей 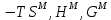 для жидкого раствора для жидкого раствораТаблица 3: Исходные данные для дальнейшего подсчета, построения графика
Расчетные формулы и пример расчета: 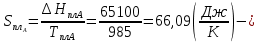 энтропия плавления компонента А энтропия плавления компонента А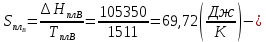 энтропия плавления компонента В энтропия плавления компонента В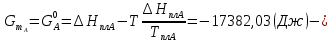 свободная энергия Гиббса А свободная энергия Гиббса А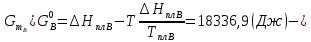 свободная энергия Гиббса В свободная энергия Гиббса В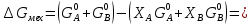 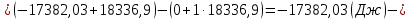 изменение свободной энергии Гиббса механической смеси изменение свободной энергии Гиббса механической смесиТаблица 4: Результаты расчета термодинамических функций для механической смеси
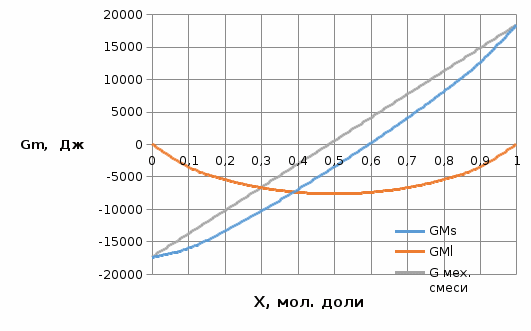 Рис.3.3 Зависимости свободной энергии Гиббса Gm от состава вещества для жидкого и твердого растворов Расчет и построение концентрационных зависимостей коэффициентов активностей и активностей компонентов в твердом и жидком растворах при Т=const. Параметры взаимодействия используются те же, что и в пункте 3. Пусть 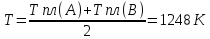 . .Расчетные формулы: Активность компонентов: 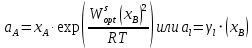 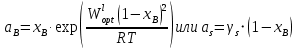 Коэффициент активности: 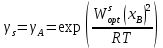 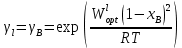 Пример расчета для 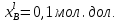 : :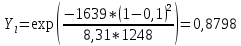 ; ;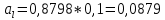 . .Таблица 5: Расчетные значения коэффициента активности в твердом и жидком растворах
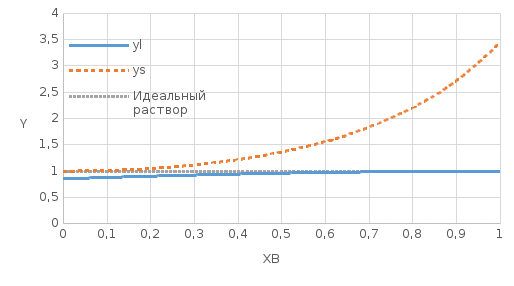 Рис.4.1 Концентрационные зависимости коэффициентов активностей компонентов в твердом, жидком и идеальном растворах Таблица 6: Расчетные значения активностей для компонентов в твердом и жидком растворах
Для идеальных растворов: 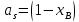 ; ; 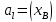 ; ; 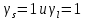 . .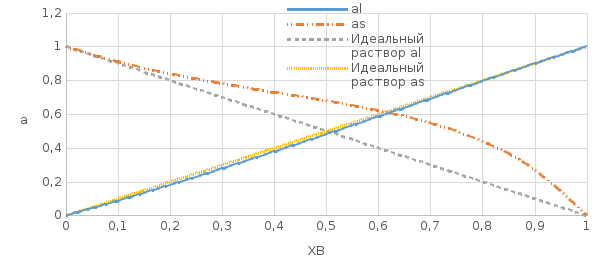 Рис.4.2 Концентрационные зависимости активностей компонентов для твердого, жидкого и идеального растворов Так как параметры взаимодействия имеют разные знаки (для aS Ws положительный, для al Wl отрицательный), то и активности для жидкого и твердого р-ров будут иметь разные знаки, т.е. будут располагаться выше и ниже линий активности для идеального р-ра. Если 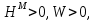 то будет положительное отклонение от идеальности, атомы А и В отталкиваются. то будет положительное отклонение от идеальности, атомы А и В отталкиваются.Расчет и построение температурной зависимости коэффициента активности компонентов А и В в твердом растворе для одного состава 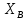 . Использовать формулы расчета из п.4 для коэффициента активности . Использовать формулы расчета из п.4 для коэффициента активностиТаблица 7: Расчетные значения для температурной зависимости коэффициента активности
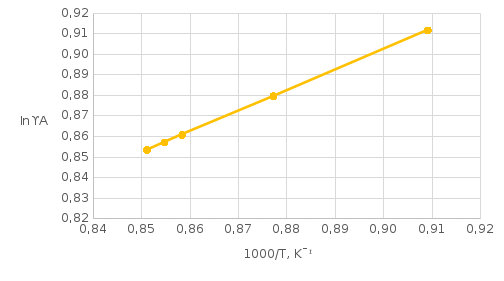 Рис.5.1 Зависимость коэффициента активности от температуры для компонента А в твердом растворе для состава XB=0,8 мол.доли. 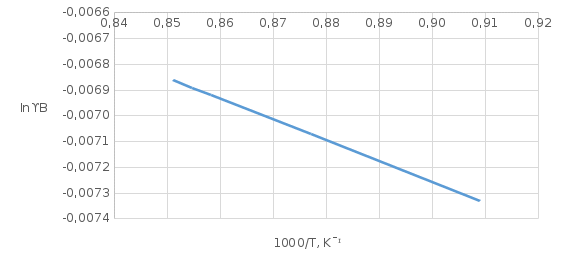 Рис.5.2 Зависимость коэффициента активности от температуры для компонента В в твердом растворе для состава XB=0,8 мол.доли. Расчет равновесных коэффициентов распределения компонентов А и B при заданной температуре. Заданная температура: 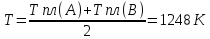 . .Для компонента B: 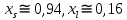 . .Для компонента A: 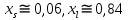 . .Расчетные формулы и сам расчет: 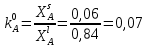 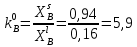 Выводы В ходе данной лабораторной работы были изучены фазовые равновесия в бинарных полупроводниковых системах с непрерывным твердым раствором методом компьютерного моделирования. Также были рассчитаны концентрационные зависимости термодинамических функций смешения, температурная зависимость коэффициента активности и коэффициенты распределения компонентов А, В при температуре 1248 К. В качестве модели, описывающей экспериментальную Т-х-проекцию диаграммы состояния, была выбрана модель регулярного раствора. Она удобна по нескольким причинам: 1) энтропия смешения определяется только конфигурационной составляющей; 2) энтальпия смешения характеризуется как линейная функция числа различных пар связей; 3) параметр взаимодействия не зависит от температуры и состава раствора. Также в лабораторной работе было исследовано влияние абсолютной величины и знака параметров взаимодействия, и было выявлено, что изменение параметров взаимодействия выше упомянутым способом приводит к изменению диаграммы состояния из типа «лист» в тип «половина листа». То есть солидус стремиться к линейному виду, в то время как ликвидус, наоборот, приобретает более явный изгиб с максимумом вблизи состава компоненты А. На графике зависимости коэффициентов активности компонентов А и В наблюдается положительное и отрицательное отклонения соответственно от модели идеального раствора. Это обосновано тем, что параметры взаимодействия имеют разные (положительный и отрицательный соответственно) знак. |

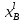 , мол.доли
, мол.доли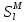 , Дж/К
, Дж/К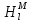 , Дж
, Дж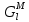 , Дж
, Дж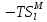
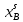 , мол.доли
, мол.доли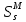 , Дж/К
, Дж/К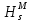 , Дж
, Дж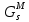 , Дж
, Дж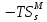
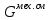 , Дж
, Дж 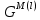 , Дж
, Дж