Моделирование искусственных нейронных сетей в среде matlab
 Скачать 348 Kb. Скачать 348 Kb.
|
|
РОСЖЕЛДОР Государственное образовательное учреждение высшего профессионального образования Ростовский государственный университет путей сообщения (РГУПС) С.М. Ковалев, А.Е. Хатламаджиян МОДЕЛИРОВАНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ В СРЕДЕ MATLAB Учебно-методическое пособие к лабораторным работам Ростов-на-Дону 2008 УДК 681.3.06 : 519.711.3(07) + 06 Ковалев, С.М. Моделирование искусственных нейронных сетей в среде MATLAB: Учебно-методическое пособие к лабораторным работам / С.М. Ковалев, А.Е. Хатламаджиян ; Рост. гос. ун-т путей сообщения. – Ростов н/Д, 2008. – 35 с. : ил. Библиогр. 3 назв. Рассмотрены основные парадигмы искусственных нейронных сетей и методы их обучения. Приводится методика выполнения лабораторных работ с использованием инстументальных средств компьютерной среды математического моделирования MATLAB. Предназначено для студентов изучающих дисциплину «Математическое моделирование систем и процессов», а также может быть полезно научным работникам и аспирантам. Учебно-методическое пособие одобрено к изданию кафедрой «Автоматика и телемеханика на ж.-д. транспорте» РГУПС. Рецензент канд. техн. наук, доц. Д.В. Швалов (РГУПС) Учебное издание Ковалев Сергей Михайлович Хатламаджиян Агоп Ервандович МОДЕЛИРОВАНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ В СРЕДЕ MATLAB Учебное пособие Редактор Молодцова Ю.Ю. Корректор Молодцова Ю.Ю. Подписано в печать . Формат 60х84/16. Бумага офсетная. Ризография. Усл. печ. л. 2,09. Уч.-изд. л. 2,00. Тираж 100 экз. Изд. № 247. Заказ № Ростовский государственный университет путей сообщения. Ризография РГУПС. Адрес университета: 344038, г. Ростов н/Д, пл. Ростовского Стрелкового Полка Народного Ополчения, 2. © Ростовский государственный университет путей сообщения, 2008 Оглавление Введение Лабораторная работа № 1. ИЗУЧЕНИЕ СВОЙСТВ ЛИНЕЙНОГО НЕЙРОНА И ЛИНЕЙНОЙ НЕЙРОННОЙ СЕТИ 1 ЦЕЛЬ РАБОТЫ 2 СВЕДЕНИЯ ИЗ ТЕОРИИ 2.1 Модель нейрона 2.2 Алгоритм обучения по дельта-правилу 2.3 Описание основных функций 3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 4 КОНТРОЛЬНЫЕ ВОПРОСЫ Лабораторная работа № 2. ИЗУЧЕНИЕ МНОГОСЛОЙНОГО НЕЛИНЕЙНОГО ПЕРСЕПТРОНА И АЛГОРИТМА ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ 1 ЦЕЛЬ РАБОТЫ 2 СВЕДЕНИЯ ИЗ ТЕОРИИ 2.1 Алгоритм обратного распространения ошибки 2.2 Описание основных функций 3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 4 КОНТРОЛЬНЫЕ ВОПРОСЫ Лабораторная работа № 3. ИЗУЧЕНИЕ РАДИАЛЬНЫХ БАЗИСНЫХ, ВЕРОЯТНОСТНЫХ НЕЙРОННЫХ СЕТЕЙ, СЕТЕЙ РЕГРЕССИИ 1 ЦЕЛЬ РАБОТЫ 2 СВЕДЕНИЯ ИЗ ТЕОРИИ 2.1 Радиально-базисные сети. Сети регрессии. Вероятностные НС 2.2 Описание основных функций 3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 4 КОНТРОЛЬНЫЕ ВОПРОСЫ Библиографический список Введение Нейронные сети – это раздел искусственного интеллекта, в котором для обработки сигналов используются явления, аналогичные происходящим в нейронах живых существ. Важнейшая особенность сети, свидетельствующая о ее широких возможностях и огромном потенциале, состоит в параллельной обработке информации всеми звеньями. При громадном количестве межнейронных связей это позволяет значительно ускорить процесс обработки информации. Во многих случаях становится возможным преобразование сигналов в реальном времени. Кроме того, при большом числе межнейронных соединений сеть приобретает устойчивость к ошибкам, возникающим на некоторых линиях. Функции поврежденных связей берут на себя исправные линии, в результате чего деятельность сети не претерпевает существенных возмущений. Другое не менее важное свойство – способность к обучению и обобщению накопленных знаний. Нейронная сеть обладает чертами искусственного интеллекта. Натренированная на ограниченном множестве данных сеть способна обобщать полученную информацию и показывать хорошие результаты на данных, не использовавшихся в процессе обучения. Характерная особенность сети состоит также в возможности ее реализации с применением технологии сверхбольшой степени интеграции. Различие элементов сети невелико, а их повторяемость огромна. Это открывает перспективу создания универсального процессора с однородной структурой, способного перерабатывать разнообразную информацию. В учебно-методическом пособии в краткой форме приведены теоретические сведения об основных парадигмах НС и примеры их реализации в компьютерной среде математического моделирования MATLAB для решения типовых задач. Лабораторная работа № 1 ИЗУЧЕНИЕ СВОЙСТВ ЛИНЕЙНОГО НЕЙРОНА И ЛИНЕЙНОЙ НЕЙРОННОЙ СЕТИ 1 ЦЕЛЬ РАБОТЫ Изучить свойства линейного нейрона и линейной нейронной сети. 2 СВЕДЕНИЯ ИЗ ТЕОРИИ 2.1 Модель нейрона Искусственные нейронные сети (НС) представляют собой простейшие математические модели мозга. Понять основные принципы построения НС можно, рассматривая их как совокупность (сеть) отдельных структур (нейронов). Очень грубо структуру биологического нейрона можно описать следующим образом. Нейрон имеет сому – тело, дерево входов – дендриты, выход – аксон. На соме и на дендритах располагаются окончания аксонов других нейронов, называемых синапсами. Принятые синапсами входные сигналы стремятся либо возбудить нейрон, либо затормозить. Когда суммарное возбуждение достигает некоторого порога, нейрон возбуждается и посылает по аксону сигнал другим нейронам. Каждый синапс обладает уникальной синаптической силой, которая пропорционально своему значению изменяет передаваемый на нейрон входной сигнал. В соответствии с приведенным описанием математическая модель нейрона представляет собой суммирующий пороговый элемент (рис. 1). 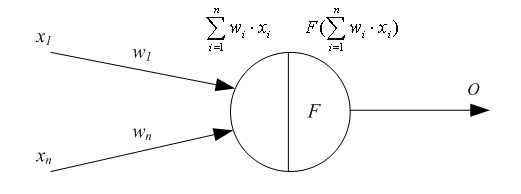 Рис. 1. Искусственный нейрон Формула срабатывания нейрона: 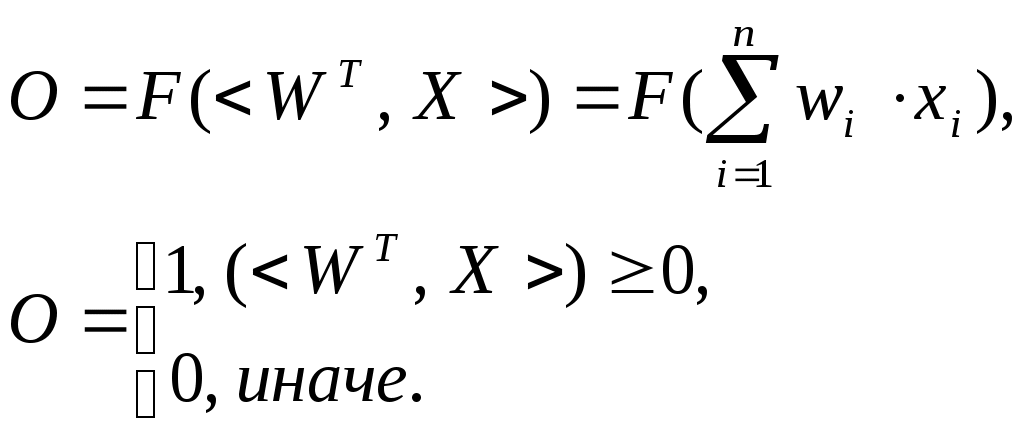 2.2 Алгоритм обучения по дельта-правилу Обучение НС происходит на некоторой обучающей выборке, для каждого образца которой определяются и сравниваются с желаемыми значениями все текущие выходы. Если разница недопустима, то веса изменяются. Окончанием обучения считается ситуация, когда общая ошибка на всех образцах допустима. Все алгоритмы обучения нейросетей являются разновидностями алгоритма обучения по методу коррекции ошибки, которая осуществляется по-разному. Идея изменения весов НС сводится к нахождению общей меры качества сети, в качестве которой обычно выбирают функцию ошибки сети. Тогда, чтобы подобрать нужные веса, необходимо минимизировать функцию ошибки. Самым распространенным методом поиска минимума является метод градиентного спуска. Для случая функции с одной переменной веса изменяются в направлении, противоположном производной, т. е. справедлива формула где h – некоторый уровень обучения, шаг изменения; F'(W) – производная функции качества НС для одной переменной. Для функции F от n переменных и единичного вектора е в пространстве Rn||е|| = 1, Для случая е = (0, 0...1...0) определим частный дифференциал Таким образом, антиградиент – это набор следующих дифференциалов: Для определения обобщенной функции ошибки рассмотрим обучающую выборку {(хk, yk)}, где k = 1, ..., К. Накопленная по всем эпохам ошибка 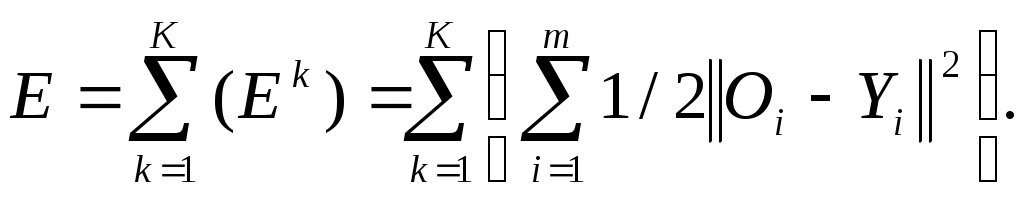 Формула модификации весов НС уточняется для различных видов функции активации. Для линейной функции F(t) = t, НС формирует каждый выход как скалярное произведение весов на вектор входов: где Yi – желаемый выход; Oi – полученный выход; X – вектор выхода. Таким образом, получаем формулу изменения весов Если значением что является алгоритмом обучения по 2.3 Описание основных функций Для работы с нейронными сетями необходимо инсталлировать MATLAB и обладать первоначальными знаниями относительно языка системы. Поскольку MATLAB представляет собой интерпретатор, то обучение инструментарию нейронных сетей заключается в основном в изучении функций и их параметров. Узнать возможности нейрона как классификатора простых линейно сепарабельных задач можно путем проведения экспериментов с моделью одного линейного нейрона. Функция newp. Для того чтобы создать нейрон, используют функцию newp, имеющую следующий синтаксис: где PR – матрица минимальных и максимальных R входных элементов; S – количество нейронов (при создании одного нейрона S=1); TF – функция активации (transfer function); LF – имя функции обучения нейрона. В случае если параметры функции newp не заданы, их значения определяются посредством ввода значений в диалоговые окна. Построенный нейрон характеризуется функциями весов (weight function), входов сети (net input function) и определенной функцией активации. Функция весов – это умножение весов на входной сигнал, функция входов сети – их сумма. Веса задаются как для входов нейрона, так и для фиксированного входа, задающего порог срабатывания (bias). Вектор весов инициализируется нулями. Для обучения используются функции, рассмотренные ниже. Функция learnp настраивает веса нейрона. Синтаксис функции обучения довольно сложен: 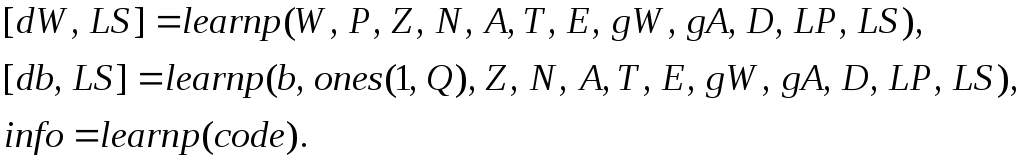 Функция learnp (W, P, Z, N, A, T, E, gW, gA, D, LP, LS) имеет несколько входов, где вектор W – вектор весов; Р – вектор входов; Z – вектор взвешенных входов; N – вектор сети; А – вектор выхода; Т – вектор желаемых выходов; Е – вектор ошибок; gW – вектор изменения весов; gA – изменения выходов. Функция возвращает значения: dW – изменения матрицы весов; LS – новый уровень обученности. Функция learnp может быть использована с параметрами по умолчанию: Использование пустого списка [ ] означает параметр по умолчанию. Функция learnp вычисляет изменение весов dW для заданного нейрона в соответствии с правилом обучения персептрона: 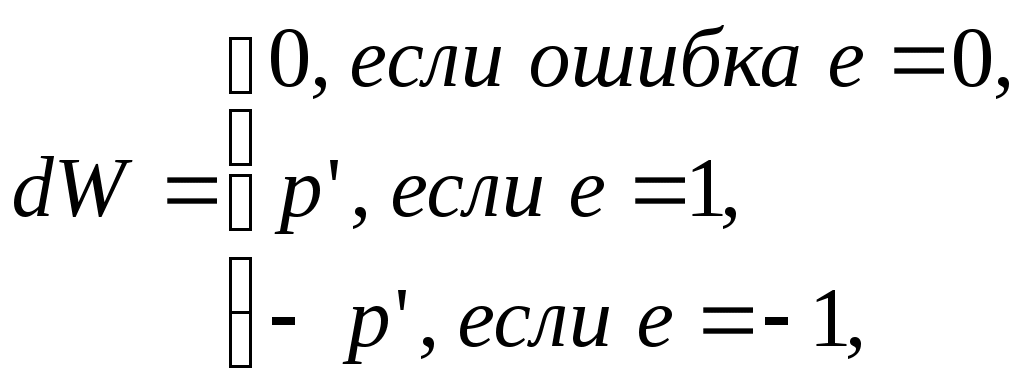 т. е. Функция learnpn настраивает нормализованные веса: Функция learnpn вычисляет изменение весов dW для данного нейрона и его входа Р и ошибки Е в соответствии с нормализованным правилом обучения персептрона: 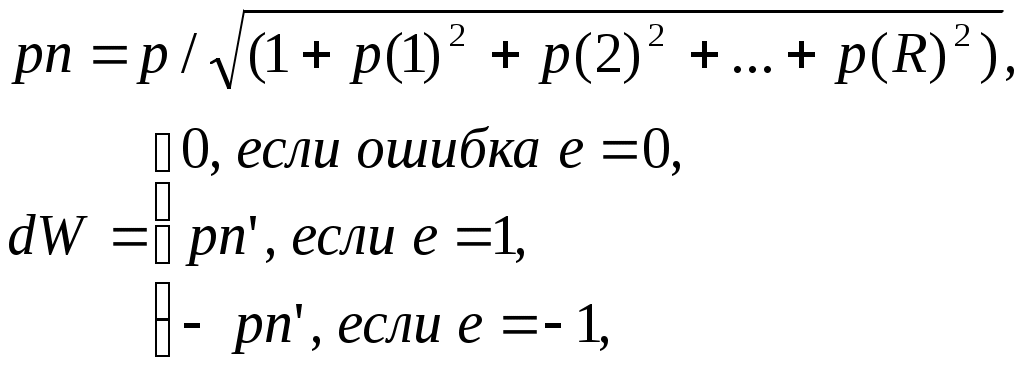 т. е. Линейный нейрон имеет одно существенное ограничение. Входные векторы должны быть линейно разделимы. Если векторы невозможно отделить прямой или гиперплоскостью, то персептрон не способен решить задачу классификации. Функция adapt адаптирует НС к условиям задачи: Параметры функции adapt: net – имя сети; Р – входы сети; T – желаемый выход; Рi – исходные условия задержки; Ai – исходные условия задержки для слоя. Функция возвращает параметры адаптированной сети net.adaptParam: net – измененная сеть; Y – выход сети; Е – ошибки сети; Pf – условия задержки входов; Af – условия задержки слоя. Параметры Рi и Pf необязательные и необходимы только для сетей, имеющих задержки на входах и слое. Функция train также обучает НС и использует следующий синтаксис: Функция train имеет следующие параметры: net – сеть; Р – входы сети; Т – желаемый выход; Рi – исходные условия задержки входа; Ai – исходные условия задержки слоя. Функция sim имитирует нейронную сеть: где net – сеть; Р – входы сети; Pi — исходные условия задержки входов сети; Ai – исходные условия задержки слоя. Функция возвращает Y – выходы сети; Pf – окончательные условия задержки входов; Af – окончательные условия задержки слоя. Функции активации. Ниже представлены назначения этих функций.
Функции графического интерфейса и вспомогательные функции. Назначение этих функций представлено ниже.
|
