Моделирование искусственных нейронных сетей в среде matlab
 Скачать 348 Kb. Скачать 348 Kb.
|
|
Функция newrbeпроектирует радиальную базисную сеть с нулевой ошибкой для заданных векторов. Функция newrbe(P, T, spread) имеет три параметра: Р –матрица Q входных векторов размерности R на Q; Т –матрица Q целевых векторов – описателей класса размерности S на Q;spread –разброс радиальной базисной функции, по умолчанию 1,0. Функция создает радиальную базисную сеть. Функция newgrnn проектирует НС регрессии – это вид радиальной базисной сети, которая часто используется для аппроксимации функций и быстро строит сеть для аппроксимации: net = newgrnn(P, T, spread). Функция newgrnn(P, T, spread) имеет следующие входы: Р – матрица Q входных векторов размерности R на Q; Т –матрица Q целевых векторов классов размерности S на Q;spread – разброс радиальных базисных функций, по умолчанию 1,0. Функция возвращает НС регрессии. Чем больше разброс, тем более гладкой будет функция аппроксимации. Для того чтобы настроить функцию аппроксимации на исходные данные, используют разброс меньший, чем типичное расстояние между входными векторами. Функция newgrnn создает двухслойную сеть. Первый слой содержит радиальные базисные нейроны, вычисляющие расстояние между входами и весами с помощью netprod. Второй слой имеет нейроны с функцией активации purelin. Только у первого слоя существует bias. Функция newpnn создает вероятностную НС, проектируемую с помощью функции net = newpnn(P, T, spread). Вероятностная НС – это вид радиальной базисной сети, как и НС регрессии, но данные сети используются для решения задачи классификации, а не аппроксимации. Функция net = newpnn(P, T, spread) имеет такие же параметры, как и вышеописанная функция newgrnn. Если разброс близок к нулю, вероятностная НС действует как классификатор на основе принципа выбора «ближайшего соседа», в противном случае сеть принимает в расчет несколько близких векторов. 3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ ПРИМЕР 1 Создание и обучение НС регрессии Рассмотрим проектирование НС регрессии. Определим: % входы НС регрессии P = [1 2 3]; % выходы НС регрессии T = [3.0 5.1 4.8]; Воспользуемся функцией newgrnn для создания НС регрессии. Зададим разброс радиальных базисных функций (переменная spread) меньше, чем 1, для того чтобы получить хорошую аппроксимацию данных и более гладкую функцию. % установка разброса радиальных базисных функций spread = 0.8; % создание НС регрессии net = newgrnn(P, T, spread); % имитация работы НС регрессии A = sim (net, P); % изображение аппроксимируемой функции plot(P, T, '.', 'markersize', 30); % установка режима добавления графиков на координатные оси hold on; % изображение работы необученной НС регрессии plot(P, A, '.', 'markersize', 30, 'color', [1 0 0]); % очистка координатных осей cla reset; % установка нового входа НС регрессии p = 4.5; % получение отклика НС регрессии a = sim (net, p); % изображение аппроксимируемой функции plot(P, T, '.', 'markersize', 30); % установка диапазонов осей X и Y axis ([0 9 -1 4]); % включение режима добавления графиков hold on; % изображение отклика НС регрессии на вход р plot(p, a, '.', 'markersize', 30, 'color', [1 0 0]); % написать заголовок графика title('Новый входной вектор '); % пометить ось X xlabel('P и p'); % пометить ось Y ylabel('T и a'); % очистить координатную сетку cla reset; % определить последовательность входов P2 P2 = 0: 0.2 : 9; Сымитируем отклик сети для различных значений, чтобы увидеть результат аппроксимации (рис. 9). 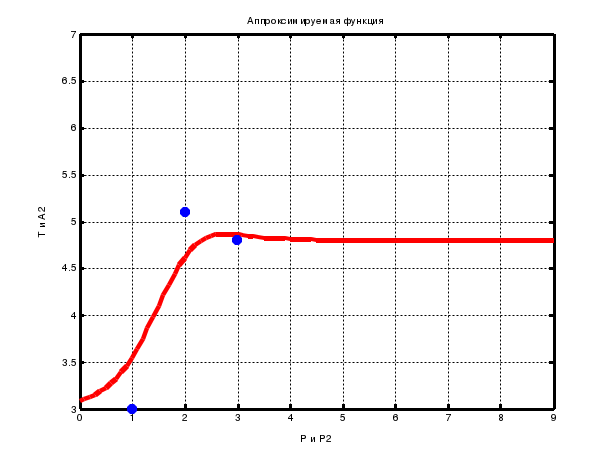 Рис. 9. Аппроксимация точек с помощью нейронной сети регрессии % получить отклик НС регрессии на последовательностьвходов Р2 A2 = sim (net, P2); % изобразить отклик НС регрессии plot(P2, A2, 'linewidth', 4, 'color', [1 0 0]); % включить режим добавления графиков hold on; % изобразить аппроксимируемую функцию plot(P, T, '.', 'markersize', 30); % установить диапазон осей axis ([0 9 3 7]); % озаглавить график title ('Аппроксимируемая функция'); % пометить ось X xlabel('Р и Р2'); % пометить ось Y ylabel('Т и А2'); ПРИМЕР 2 Использование РБНС для аппроксимации функций Рассмотрим аппроксимацию функций на основе радиальной базисной сети. % определение диапазона значений радиальной базисной функции P = -4 : 0.1 : 4; % вычисление радиальной базисной функции на диапазоне P a = radbas (P); % изображениеРБФ plot (P, a); % озаглавить график title('Радиальная базисная функция'); % пометить ось X xlabel('Вход P'); % пометить ось Y ylabel ('Выход а'); На рис. 10 изображена радиальная базисная функция. Функция newrbe создаст необходимую сеть. Зададим аппроксимируемую функцию как набор точек: % определение последовательности аргументов % аппроксимируемой функции Р P = -1 : 0.1 : 1; % определение значений аппроксимируемой функции, % соответствующих Р T = [-.6662 -.3766 -.1129 .2111 .6565 .3301 .3649 .2006... -.1913 -.3994 -.5022 -.4531 -.1133 .0866 .3333 .4955... .3488 .2833 -.1112 -.6685 -.3255]; 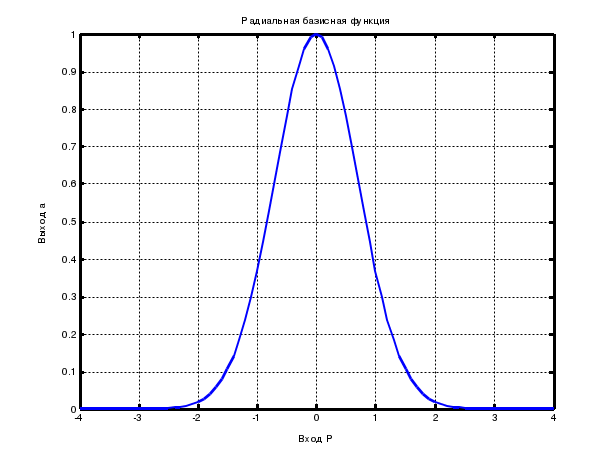 Рис. 10. Радиальная базисная функция Изобразим график функции (рис. 11). % изображение аппроксимируемой функции plot(P, T, '*'); % озаглавить график title('Обучающая выборка'); % пометить ось X xlabel('Входной вектор Р'); % пометить ось Y ylabel('Вектор Т'); Далее необходимо найти функцию, которая хорошо описывает заданные 21 точку. Функция newrb создает РБНС для аппроксимации: % целевой среднеквадратичной ошибки e = 0.02; % разброса РБФ sp = 1; % создание РБФ net = newrb(P,T,e,sp); % определение вектора входов X = -1 : 0.01 : 1; Сымитируем работу сети. % формирование отклика Y Y = sim(net, X); % включение режима добавления графика hold on; % изображение результатов аппроксимации plot(X, Y); %отключение режима добавления графика hold off; 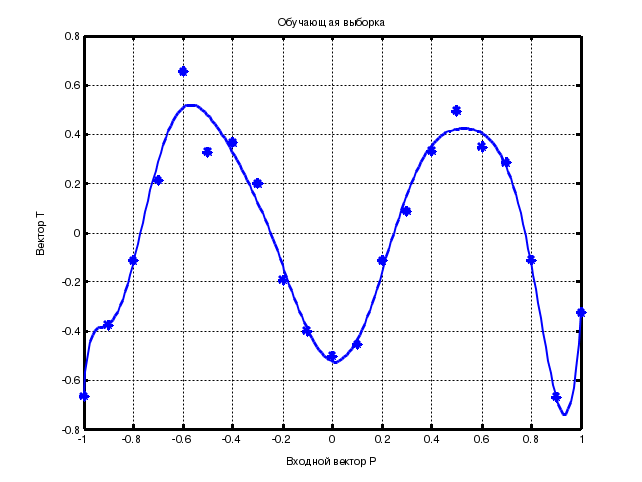 Рис. 11. Результат аппроксимации с помощью радиальной базисной нейронной сети ПРИМЕР 3 Использование вероятностной НС для классификации векторов Рассмотрим задачу классификации с набором входов Р и множеством классов, обозначенным Тс. % определение входов P = [1 2 3 4 5 6 7]; % определение желаемых выходов Tc =[1 1 3 3 2 1 1]; % конвертирование индексов в векторы, содержащие1 % в индексных позициях T = ind2vec (Tc); % создание вероятностной НС net = newpnn (P, T); % имитация работы вероятностной НС Y = sim(net, P); % конвертирование номеров классов в векторы. Yc = vec2ind(Y); 4 КОНТРОЛЬНЫЕ ВОПРОСЫ Какую функцию называют радиальной базисной функцией? Из каких слоев состоит радиально-базисная НС? Из каких слоев состоит НС регрессии? Из каких слоев состоит вероятностная НС? Какие виды НС предназначены для решения задачи аппроксимации функций, а какие – для классификации объектов? Какие типы НС создаются в среде MATLAB с помощью функций newrb, newrbe, newgrnn, newpnn? Библиографический список 1 Осовский, С. Нейронные сети для обработки информации : пер. с польск. / С. Осовский. – М. : Финансы и статистика, 2002. 2 Ярушкина, Н.Г. Основы теории нечетких и гибридных систем : учеб. пособие / Н.Г. Ярушкина. – М. : Финансы и статистика, 2004. 3 Медведев, В.С. Нейронные сети. MATLAB 6 / В.С. Медведев, В.Г. Потемкин; под общ. ред. В.Г. Потемкина. – М. : ДИАЛОГ-МИФИ, 2002. |
