Моделирование искусственных нейронных сетей в среде matlab
 Скачать 348 Kb. Скачать 348 Kb.
|
|
Структура данных описания нейронных сетей. Структура данных net – это описание обученной НС. Обучение осуществляется в соответствии со следующими параметрами, значения которых либо устанавливаются пользователем, либо по умолчанию.
Структура данных описания адаптированной НС net.adaptfcn включает в себя следующие поля net.adapt.param: NET – адаптированная НС; Y – выходы НС; Е – ошибки НС; Pf – окончательные входные значения задержек; Af – окончательные выходные задержки; TR – результат обучения (эпохи и целевая ошибка). Проведем в среде Matlab toolbox эксперименты, используя рассмотренные функции. 3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ ПРИМЕР 1 Создание нейронов, реализующих функции логического И и логического ИЛИ Создадим нейрон с одним двухэлементным входом (интервалы первого и второго элементов [0; 1]). Определим два первых параметра функции newp, а в качестве значений третьего и четвертого параметра (типа функции активации и имени процедуры обучения) воспользуемся значениями по умолчанию. % создание нейрона с одним двухэлементным входом (интервал % первого элемента [0; 1] и интервал второго элемента [-2; 2] net = newp([0 1; -2 2], 1); Для того чтобы исследовать поведение нейрона, необходимо имитировать его работу с помощью функции sim. Для определения последовательности значений входа создадим последовательность Р1. % создание последовательности значений входа P1 = {[0; 0] [0; 1] [1; 0] [1; 1]}; % имитация работы нейрона net на последовательности входов Р % желаемых выходов – Т1, которая позволит нам провести адаптацию % нейрона (обучить его) через 20 проходов. Y = sim (net, P1); % создание последовательности выходов T1 = {0, 0, 0, 1}; % установка количества проходов (циклов) адаптации net.adaptParam.passes = 20; %адаптация нейрона net для обучающей выборки <Р1; Т1> net = adapt (net, P1, T1); % симуляция работы нейрона net на последовательности входов P1 Y = sim (net, P1); В результате мы получим нейрон, выполняющий функцию логического И. Для переобучения нейрона на выполнение функции ИЛИ переопределим входы Р и выходы Т. % создание последовательности входов P2 = [0 0 1 1; 0 1 0 1]; % создание последовательности выходов (реакций)для нейрона, % выполняющего функцию логического ИЛИ T2 = [0, 1, 1, 1]; % Инициализируем нейрон, обучим его на 20 проходах(эпохах) % инициализация нейрона net net = init (net); % имитация работы нейрона net на последовательности входов Р2 Y = sim (net, P2); % установка количества проходов net.trainParam.epochs = 20; % обучение нейрона net на обучающей выборке <Р2, Т2> net = train(net, Р2, Т2); % имитация работы нейрона net на последовательности входов Р2 Y = sim (net, P2); Функция train выводит график обучения нейрона (рис. 2). 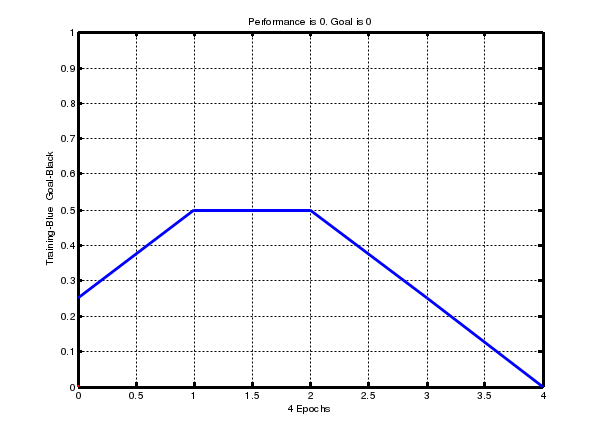 Рис. 2. График обучения нейрона Для случайного изменения весов и порога срабатывания используем функцию init.По умолчанию для создаваемого нейрона указана функция hardlim. ПРИМЕР 2 Обучение нейрона классификации векторов на две категории Начнем с классификации векторов на основе двухвходового нейрона. Будем использовать функцию newp для создания нейрона, sim для имитации его работы, adapt для адаптации (обучения) нейронной сети. Обучим двухвходовый нейрон классифицировать входные векторы на две категории. % определение четырех двухэлементных входов P = [ -0.5 -0.5 0.4 -0.2; -0.5 0.5 -0.4 1.0]; % зададим желаемые выходы нейрона для определенных векторов T = [1 1 0 0]; % изобразим входные векторы (точки) на плоскости: plotpv(P, T); 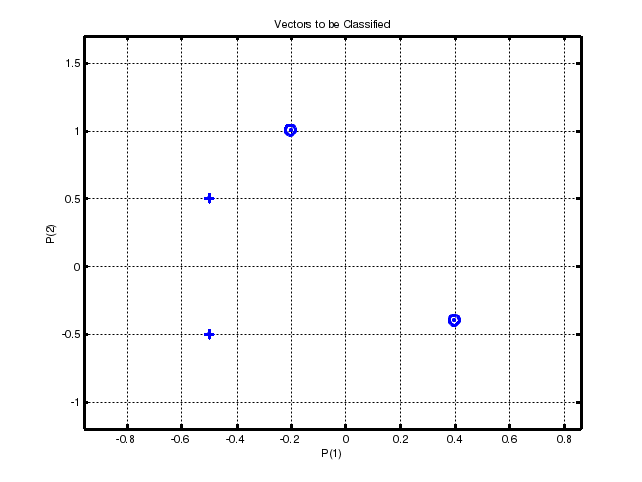 Рис. 3. Исходные векторы, предназначенные для классификации нейроном Каждый из четырех входных векторов на плоскости Р определяется двумя координатами, представленными как двухэлементные столбцы в матрице Р (рис. 3). Создадим один линейный нейрон с двумя входами, значения которых лежат в интервале [-1, 1]. % создание линейного нейрона с двумя входамииз интервала [-1, 1] net = newp([-1 1; -1 1], 1); Нейрон по умолчанию имеет функцию активации hardlim и такой нейрон разделяет входные векторы прямой линией. Определим координаты линии классификации: веса (IW) и порог срабатывания нейрона (b). % получение управляющей структуры linehandle для изображения % разделяющей линии в координатах весов (IW) и порога % срабатывания нейрона (b) linehandle = plotpc (net.IW{1}, net.b{1}); % изображение разделяющей прямой plotpc(net.IW{1}, net.b{1}); Если исходным весам задать нулевые значения, то любые входы дадут одинаковые выходы, и линия классификации не будет видна на плоскости. Проведем обучение: % очистка координатных осей cla; % изображение входных векторов двух категории, категория задается % элементами вектора Т plotpv(P, T); % получение управляющей структуры linehanctle linehandle = plotpc(net.IW{1}, net.b{1}); % присвоение начального значения ошибки E = 1; % инициализация нейрона net = init (net); % получение управляющей структуры linehandle linehandle = plotpc (net.IW{1}, net.b{1}); % организация цикла пока ошибка не равна 0 while (mse(E))', % адаптация нейрона net на обучающей выборке <Р, Т>, % функция возвращает адаптированный нейрон net, % выход Y, ошибку Е [net, Y, E] = adapt (net, P, T); % изображение разделяющей прямой нейрона после адаптации linehandle = plotpc(net.IW{1}, net.b{1}, linehandle); % очистка окна графиков drawnow; % конец цикла while end; Функция adapt возвращает новый объект – сеть, которая выполняет классификацию, выход сети и ошибку (рис. 4). Проведем классификацию нового вектора с помощью обученного нейрона на основе функции sim. Определим новый вектор P. %определение вектора Р P = [0, 6; 1, 1]; % имитация работы нейрона net, получение откликанейрона а а = sim (net, P); % изображение входа P, отнесенного нейрономк категории а plotpv (P, а); 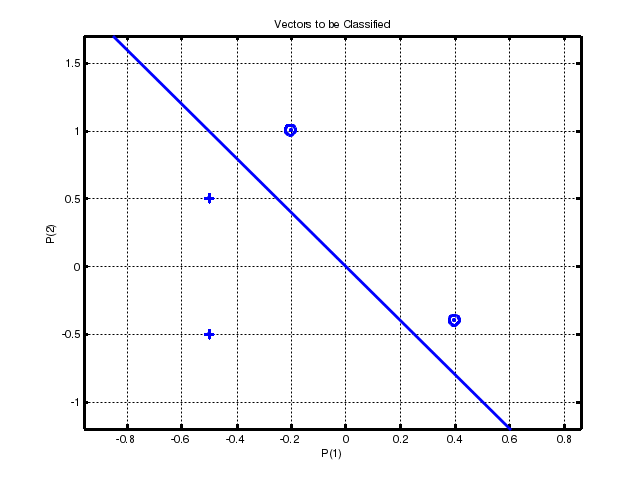 Рис. 4. Прямая, разделяющая исходные векторы на классы Обученный нейрон можно использовать для классификации любого вектора: % включить режим добавления графиков в графическом окне hold on; % изображение входных точек в соответствии с категориями Т plotpv(Р, Т); % изображение разделяющей поверхности plotpc (net.IW{1}, net.b{1}); % отключение режима добавления графиков hold off; Нейрон классифицирует новую точку, как принадлежащую категории «0» (представлена кружком), а не категории «1» (представлена +). ПРИМЕР 3 Создание слоя линейных нейронов Рассмотрим последовательность из 10 шагов (для выхода T1, который известным образом зависит от входов Р1): % последовательность входов P1 = {-1 0 0 0 1 1 -1 0 -1 1}; % последовательность выходов T1 = {-1 -1 1 0 1 2 0 -1 -1 1}; Используем функцию newlin, чтобы создать нейрон со значениями входа в интервале [-1; 1], задержками входа от 0 до 1 и уровнем обучения 0,1. % создание линейного слоя из одного нейронасо значениями входа % в интервале [-1; 1], задержками входа от 0 до 1 % и уровнем обучения 0,1. net = newlin ([-1 1], 1, [0 1], 0.1); Адаптируем нейрон к задаче одним проходом через последовательность входа. Измерим среднюю квадратичную ошибку с помощью функции mse(e). % адаптация нейрона к последовательности P1 [net, y, e, pf] = adapt (net, P1, T1); % измерение ошибки mse (e) Получим довольно большую ошибку. Вновь адаптируем сеть на 10 шагах последовательности, используя предыдущее значение pf какновое исходное значение задержки: P2 = {1 -1 -1 1 1 -1 0 0 0 1}; T2 = {2 0 -2 0 2 0 -1 0 0 1}; % адаптация с начальным вектором задержки pf [net, y, e, pf] = adapt (net, P2, T2, pf); mse (e) Адаптируем сеть на 100-разовом прогоне последовательности: % формирование новой последовательности входов P3 = [P1 P2]; % формирование новой последовательности выходов T3 = [T1 T2]; % установка количества проходов net.adaptParam.passes = 100; % адаптация нейрона [net, y, e] = adapt (net, P3, T3); Получим приемлемую ошибку, значит сеть обучена зависимости входов от выходов. 4 КОНТРОЛЬНЫЕ ВОПРОСЫ Что представляет собой математическая модель нейрона?Как выглядит формульное представление алгоритма обучения по дельта-правилу? Какое ограничение имеет линейный нейрон? Можно ли обучить линейный нейрон выполнять логическую функцию исключающего ИЛИ? Какие функции используются для настройки весов персептрона в среде MATLAB? В чем их отличие? Лабораторная работа № 2 ИЗУЧЕНИЕ МНОГОСЛОЙНОГО НЕЛИНЕЙНОГО ПЕРСЕПТРОНА И АЛГОРИТМА ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ 1 ЦЕЛЬ РАБОТЫ Изучить возможности многослойного персептрона как аппроксиматора и классификатора. 2 СВЕДЕНИЯ ИЗ ТЕОРИИ 2.1 Алгоритм обратного распространения ошибки Пусть определена трехслойная нейронная сеть с п входами, m выходами и l скрытыми между ними элементами, тогда необходимо рассмотреть и построить два слоя весов: от входов к скрытым элементам и к выходу, т. е. (W1,W2). Назначение алгоритма обратного распространения ошибки – настройка всех слоев многослойной структуры. Рассмотрим работу алгоритма на примере сети с одним скрытым слоем и одним выходом (рис. 5). Преобразования входных сигналов, задаваемые нейронной сетью, определяются следующими формулами: 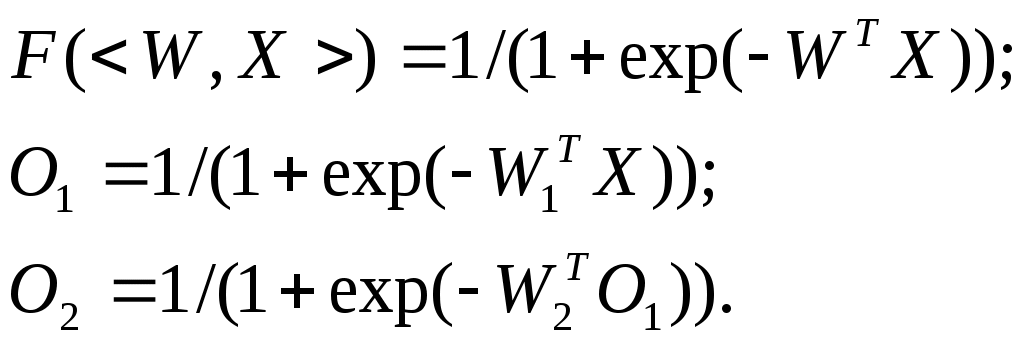 Общая функция ошибки зависит от весов всех слоев, в нашем случае от вектора W2и от матрицы W1: где Y – выход, который задан в обучающей выборке. 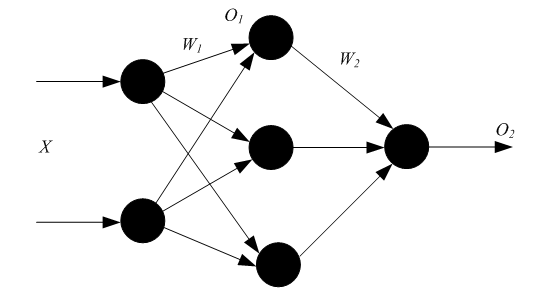 Рис. 5. Многослойный персептрон Теперь необходимо определить приращение каждого веса с помощью частных производных: 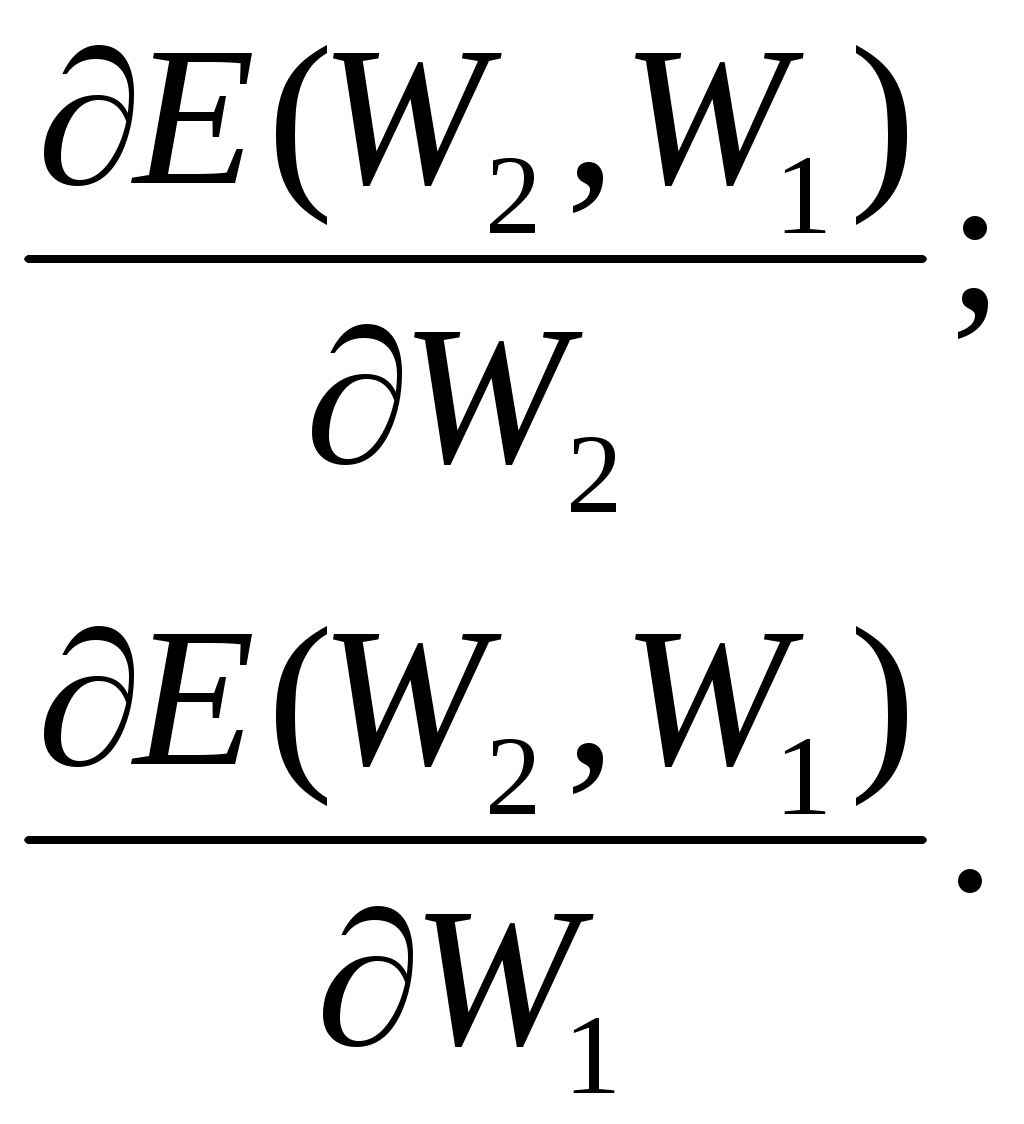 Для многослойной архитектуры частные производные ошибки по матрице весов каждого слоя определяются по формуле сложной производной. В случае униполярной сигмоиды правило изменения весов будет следующим: 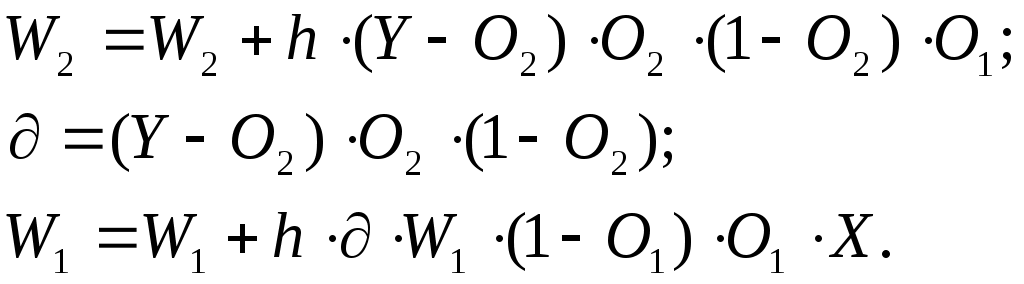 Таким образом, метод обратного распространения ошибки позволяет изменять веса промежуточных слоев, хотя желаемые значения на промежуточных слоях не заданы. 2.2 Описание основных функций Функция newff создает нейронную сеть прямого распространения сигнала, обучаемую с помощью алгоритма обратного распространения ошибки: net = newff(PR, [S1 S2 SNl], {TF1 TF2 TFNl), BTF, BLF, PF). Рассмотрим параметры функции newff:PR –матрица интервалов значений для R входных элементов, задаваемых минимальным и максимальным значениями; Si – размер i-гослоя, для N слоев; TFi–функция активации i-го слоя, по умолчанию используется функция tansig –гиперболический тангенс; BTF – функция обучения сети методом обратного распространения ошибки, по умолчанию используется функция traingdx;BLF –функция изменения весов при обучении, по умолчанию используется learngdm;PF –функция измерения ошибки, по умолчанию тsе. Функция newff возвращает многослойную нейронную сеть прямого и обратного распространения сигнала и ошибки соответственно. Функции активации могут быть выбраны из следующего перечня: гиперболический тангенс tansig,логистическая сигмоида logsig или линейная функция purelin. 3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ |
