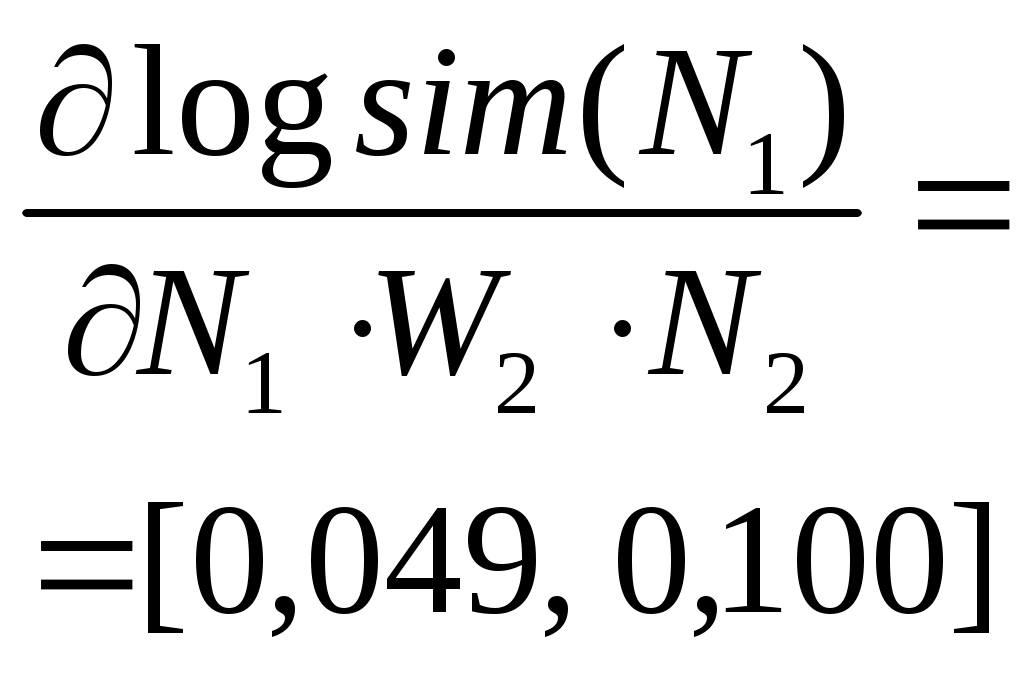Моделирование искусственных нейронных сетей в среде matlab

• Название: Моделирование искусственных нейронных сетей в среде matlab
• Дата: 22.09.2022
• Размер: 348 Kb.
• Имя файла: model_iskysstv_matlab.doc
• Тип: Учебное пособие; #691201
• страница: 3 из 4

ПРИМЕР 1 Создание и обучение нейронной сети с по­мощью алгоритма обратного распространения ошибки
Зададим с помощью графика исходную функцию:
% входы НС

P = [0 1 2 3 4 5 6 7 8];

% желаемые реакции НС

T = [0 0.44 0.88 0.11 -0.66 -0.95 -0.45 0.18 0.92];

% изображение аппроксимируемой функции

plot(P, T, 'o');
Используем функцию newff,чтобы создать двухслойную сеть прямого распространения. Пусть сеть имеет входы с интервалом значений от 0 до 8, первый слой с 10 нелинейными сигмоидальными, второй – с одним линейным нейронами. Используем для обучения алгоритм обратного распространения ошибки (backpropagation) Левенберга – Марквардта (рис. 6).
% создание двухслойной НС прямого распространения с интервалом

% значений входов от 0 до 8, причем первый слой содержит

% 10 нелинейных сигмоид, а второй — один линейный нейрон.

% Для обучения используется алгоритм обратного распространения

% ошибки (backpropagation).

net = newff([0 8], [10 1], {'tansig' 'purelin'},'trainlm');

% имитация работы необученной НС

yl = sim (net, P);

% изображение результатов работы необученной НС

plot(P, T, 'o', P, yl, 'x') ;

% Обучим сеть на 100 эпохах с целевой ошибкой 0.01:

% установка количества проходов

net.trainParam.epochs = 50;

% установка целевого значения ошибки

net.trainParam.goal = 0.01;

% обучениеНС (рис. 6)

net = train(net, P, T) ;

% имитация работы обученной НС

y2 = sim(net, P);

% изображение результатов работы НС (рис. 7)

plot(P, T, 'o', P, yl, 'x', P, y2, '+');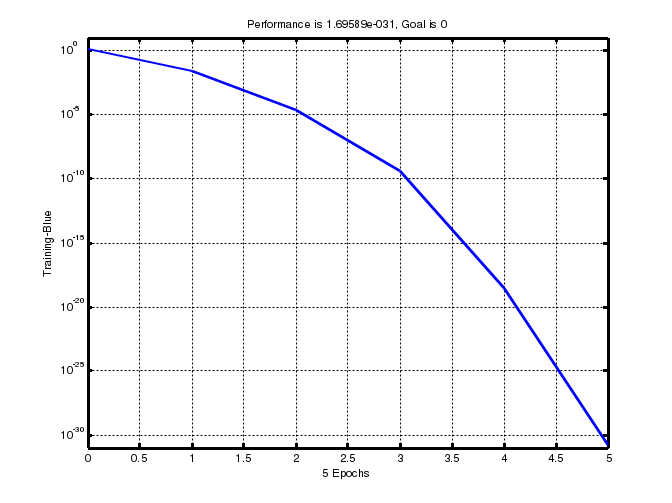



Рис. 6. График обучения двухслойного персептрона
Для исследования работы алгоритма обратного распространения ошибки воспользуемся примером, встроенным в Matlab toolbox, набрав команду demo.

В появившемся диалоговом окне необходимо последовательно выбирать пункты меню: Toolboxes->Neural Network->Other Demos->Other Neural Network Design textbook demos->Table of Contents->10-13->Backpropagation Calculation.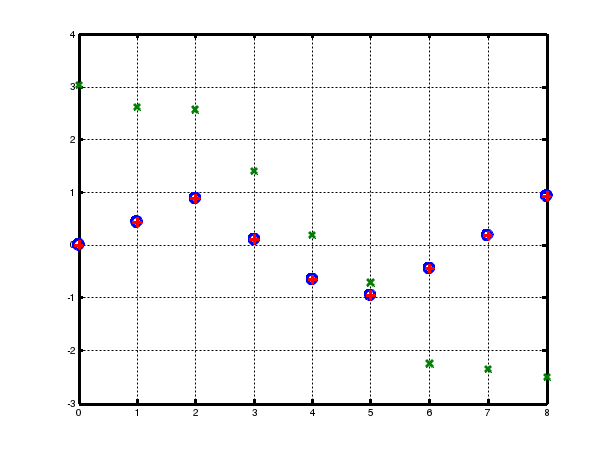

Рис. 7. Результат аппроксимации векторов двухслойным персептроном
В примере используется двухслойный персептрон с двумя нелинейными нейронами в первом слое и одним во втором. Действие алгоритма обратного распространения ошибки разбито на следующие шаги: назначение входа и желаемого вы­хода, прямой проход входного сигнала до выхода, обратное распространение ошибки, изменение весов. Переменные, по­зволяющие проследить работу алгоритма обратного распро­странения ошибки, обозначены следующим образом:

Р –входной сигнал;

W₁(i) –вектор весов первого слоя, W₁(1) –вес связи, пе­редающий входной сигнал на первый нейрон, a W₁(2) – на второй;

W₂(i) –вектор весов второго слоя, W₂(1) –вес связи, пе­редающий входной сигнал с первого нейрона во второй слой, a W₂(2) –со второго;

B₁(i) –вектор пороговых значений (bias) нейронов пер­вого слоя, i = 1, 2;

В₂– пороговое значение (bias) нейрона второго слоя;

N₁(i) – вектор выходов первого слоя, i = 1, 2;

N₂– выход второго слоя;

A₁(i) – вектор выходных сигналов первого слоя после вы­полнения функции активации (сигмоиды), i = 1, 2;

А₂– выход второго слоя после выполнения функции ак­тивации (линейной);

lr – коэффициент обучаемости.

Пусть входной сигнал Р = 1,0, а желаемый выход .

Результаты выполнения этапов алгоритма представлены в табл. 1.
Таблица 1
Результаты поэтапного выполнения алгоритма обратного распространения ошибки

Этап	Прямое распрост­ранение входного сигнала	Обратное распрост­ранение ошибки	Изменение весов
A1(1), A1(2)	Logsig(W1P+B1) = = [0,321, 0,368]	Не выполняется	Не выполняется
А2	purelin(W1P+В1)= = 0,446	То же	То же
е	t - A2 = 1,261	»	»
N1(1), N1(2)	Не выполняется		»
N2	То же		»
W1(1) W1(2)	»	Не выполняется
B1(1), B1(2)	»	То же
B2	»	»
W2(2)	»	»

4 КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Каким алгоритмом обучают многослойные НС?
   

1. 
   Из каких основных этапов состоит алгоритм обратного распространения ошибки?
   

2. 
   Почему алгоритм обратного распространения ошибки от­носится к классу алгоритмов градиентного спуска?
   
3. 
   Как влияет функция принадлежности на правило измене­ния весов в обратном алгоритме распространения ошибки?
   
4. 
   Какая функция в среде MATLAB создает НС прямого распространения?
   
5. 
   Какие функции активации могут быть назначены для нейронов НС прямого распространения?
   

Лабораторная работа № 3

ИЗУЧЕНИЕ РАДИАЛЬНЫХ БАЗИСНЫХ, ВЕРОЯТНОСТНЫХ НЕЙРОННЫХ СЕТЕЙ, СЕТЕЙ РЕГРЕССИИ
1 ЦЕЛЬ РАБОТЫ

Изучить модель вычислений радиаль­ного базисного нейрона, структуру и функции сетей регрес­сии, вероятностных нейронных сетей.
2 СВЕДЕНИЯ ИЗ ТЕОРИИ

2.1 Радиально-базисные сети. Сети регрессии. Вероятностные НС
Рассмотрим радиальный базисный нейрон с R входами. Струк­тура нейрона представлена на рис. 8. Радиальный базисный нейрон (РБН) вычисляет расстояние между векторами входов X ивектором весов W,затем умножает его на фиксированный порог b. Функция активации РБН, полученная в среде MATLAB, представлена на рис. 10. Ра­диальная базисная функция имеет максимум, равный 1, когда ее входы нулевые. Следовательно, радиальный базисный ней­рон действует как детектор, который получает на выходе 1, когда вход X идентичен его вектору весов W. Фиксированный порог b даст возможность управлять чувствительностью ней­рона. Например, если нейрон имеет порог 0,1, то выход равен 0,5 для любого входного вектора X, находящегося на вектор­ном расстоянии 8,326 (8,326/b) от W.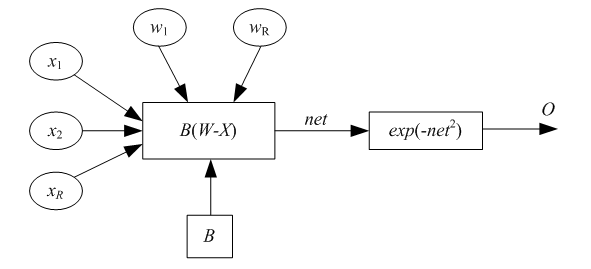



Рис. 8. Радиальный базисный нейрон
Радиальная базисная нейронная сеть (РБНС) состоит из двух слоев: скрытого радиального базисного слоя из S¹нейронов и выходного линейного слоя из S²нейронов. Элементы первого слоя РБНС вычисляют расстояния между входным вектором и векторами весов первого слоя, сформированных из строк матрицы W ^2,1. Вектор порогов В и расстояния поэлементно умножаются. Выход первого слоя можно выразить формулой

где A¹ – выход первого слоя; функция radbas – радиально-базисная функция; W – матрица весов первого слоя сети; X – входной вектор; В – вектор порогов первого слоя.

Согласно формуле радиальные базисные нейроны с век­тором весов, близким к X, сгенерируют значения, близкие к 1. Если нейрон имеет выход 1, то это значение весами второго слоя будет передано на его линейные нейроны. Фактически радиальный базисный нейрон с выходом 1превращает выхо­ды всех остальных нейронов в нули. Тем не менее, типичным является случай, когда несколько нейронов дают на выходах значимый результат, хотя и с разной степенью.

Радиальные базисные нейронные сети обучаются в три этапа. Опишем этапы обучения.

Первый этап – выделение центров (весов). Центры, представленные в РБН-слое, оптимизируются первыми с помощью обучения без учителя. Центры могут быть выделены разными алгоритмами, в частности обучением Кохонена. Ал­горитмы должны разместить центры, отражая кластеризацию исходных данных.

Второй этап – назначение отклонений. Отклонения могут быть назначены различными алгоритмами, например алгоритмом «ближайшего соседа».

Третий этап – линейная оптимизация. Можно ис­пользовать методы обучения по дельта-правилу, обратному распространению ошибки.

Нейронные сети регрессии (НСР) имеют такой же, как и РБНС, первый слой, но второй слой строится специальным образом. Для аппроксимации функций часто используются обобщенные сети регрессии (generalized regression neuron net­works). Второй слой, как и в случае РБНС, выполняет поэле­ментное произведение строки W_1,2и вектора выхода первого слоя a¹. Он имеет столько нейронов, сколько существует целевых пар <входной вектор/целевой вектор>. Матрица весов W – это на­бор целевых строк. Целевое значение – это значение аппрок­симируемой функции в обучающей выборке. Предположим, имеется один входной вектор х_i,который сгенерирует на выходе первого слоя выход, близкий к 1. В результате выход второго слоя будет близок к t_iодному из значений аппроксимируемой функции, использованной при формировании второго слоя.

Сети регрессии иногда называют Байесовскими вероятно­стными сетями регрессии, или обобщенными НС регрессии. Некоторые реализации сетей регрессии имеют четыре слоя: входной, выходной, слои радиальных центров, элементов рег­рессии. Радиальный слой представляет собой центры-класте­ры известных обучающих данных и содержит такое же коли­чество элементов, как обучающая выборка; РБН обучаются алгоритмом кластеризации. Слой регрессии имеет только на один элемент больше, чем выходной слой, и содержит линей­ные элементы одного из двух типов. Элемент первого типа вычисляет условную вероятность каждого выходного атрибу­та, элемент второго типа вычисляет плотность вероятности. Выходной слой выполняет специальные функции деления. Каждый элемент делит выходы, ассоциированные первым ти­пом, с помощью элементов второго типа.

Байесовские вероятностные НС используются только для проблем классификации. Они содержат четыре слоя: вход­ной, выходной, слой РБН и элементов линейной классифи­кации. Слои могут содержать квадратную матрицу потерь, включение которой возможно, только если третий и четвер­тый слои состоят из одинакового числа элементов. Радиаль­ные базисные нейроны в таких сетях используются для хра­нения образцов, взятых из обучающей выборки, которая бе­рется полностью. Следовательно, первый скрытый слой содержит такое же количество элементов, что и обучающая выборка. Так как элементы слоя классификации связаны с выходом каждого класса, можно оценить вероятность принадлежности последнему. Если используется матрица потерь, то цена решения минимальна. Такие сети обычно быстро тре­нируются, но медленно вычисляют из-за большого размера.

Вероятностные нейронные сети (ВНС, probabilistic neuron networks) используются для решения проблемы классифика­ции. Первым слоем в архитектуре ВНС является слой радиальных базисных нейронов, который вычисляет расстояние и век­тор индикаторов принадлежности другим входным векторам, используемым при обучении. Второй слой суммирует эти зна­чения для каждого класса входов и формирует выходы сети, как вектор вероятностей. Далее специальная функция активации (compete) определяет максимум вероятностей на выходе второ­го слоя и устанавливает данный выход в 1, а остальные выходы в 0. Матрица весов первого слоя W^1,1 установлена в соответ­ствии с обучающими парами. Блок расчета расстояний полу­чает вектор, элементы которого показывают, насколько близок входной вектор к векторам обучающего множества. Элементы вектора умножаются на вектор порогов и преобразуются ра­диальной базисной функцией. Входной вектор, близкий к не­которому образцу, устанавливается в 1 в выходном векторе первого слоя. Если входной вектор близок к нескольким образцам отдельного класса, то несколько элементов выходного вектора первого слоя будут иметь значения, близкие к 1.

Веса второго слоя W^1,1устанавливаются по матрице T целевых векторов, каждый вектор которой включает значение 1 в строке, связанной с определенным классом входов, и нули в остальных позициях. Произведения Т a¹ суммируют эле­менты выходного вектора первого слоя а¹ для каждого из K классов. Затем функция активации второго слоя (compete) ус­тановит значение 1 в позицию, соответствующую большему элементу выходного вектора, и 0 во все остальные. Следова­тельно, сеть классифицирует входные векторы, назначая вхо­ду единственный класс на основе максимальной вероятности принадлежности.
2.2 Описание основных функций
Функция newrb создает радиальную базисную сеть и имеет следующий синтаксис:
net = newrb(P, Т, goal, spread).
Радиальные базисные сети используют для аппроксимации функций. Функция newrb конструирует скрытый (первый) слой из радиальных базисных нейронов и использует значение средней квадратичной ошибки (goal). Функция newrb(P, Т, goal, spread) имеет следующие аргументы: Р – матрица Q входных векторов размерности R на Q; Т – матрица Q векторов целевых классов S на Q; goal –средняя квадратичная ошибка, по умолчанию 0,0; spread – разброс радиальной ба­зисной функции, по умолчанию 1,0. Функция создает и возвращает в качестве объекта радиальную базисную сеть. Большое значение разброса приводит к большей гладкости аппроксимации. Слишком большой разброс требует много нейронов, для того чтобы подстроиться под быстро изменяющуюся функцию, слишком малый – для достижения гладкости аппроксимации. Подобрать значение разброса можно с помощью многократных вызовов функции newrb. Создадим в среде MATLABрадиальную базисную сеть:
net = newrbe(P, T, spread).