Философ. и метод науки. Моделирование переходных процессов в синхронном генераторе при разноудаленных коротких замыканиях
 Скачать 33.02 Kb. Скачать 33.02 Kb.
|
|
УО «ПОЛОЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» КАФЕДРА СОЦИАЛЬНО-ГУМАНИТАРНЫХ ДИСЦИПЛИН РЕФЕРАТ ПО ФИЛОСОФИИ И МЕТОДОЛОГИИ НАУКИ На тему «Моделирование переходных процессов в синхронном генераторе при разноудаленных коротких замыканиях» Магистранта Фамилия Шпака Имя Константина Отчество Вацлавовича Кафедра Энергетики и электроники Содержание Объект, предмет, цель и задачи диссертационного исследования 3 Методология диссертационного исследования 4 Анализ основных источников по теме диссертационного исследования 9 Список литературы 14 Объект, предмет, цель и задачи диссертационного исследования Объектом данного исследования является переходный процесс, предметом же является энергосистема в целом. Целью является определение влияния коротких замыканий на энергооборудование энергосистемы, определение параметров уставок релейной защиты и автоматики. Задачу можно сформулировать как определение влияния переходных процессов на генерирующие мощности и на энергосистему в целом. Методология диссертационного исследования Математическое моделирование— это процесс изучения динамических свойств систем на основе решения дифференциальных или алгебраических уравнений, адекватно описывающих свойства реальных систем. По форме представления математических моделей [3] различают инвариантную, алгоритмическую, аналитическую и графические модели объекта. Инвариантная (безвариантная) форма — математическая модель, представленная системой уравнений (дифференциальных, алгебраических) вне связи с методом решения этих уравнений. Алгоритмическая форма — модель, связанная с выбранным численным методом решения и записанная в виде алгоритма (последовательности вычислений). Аналитическая модель представляет собой явные зависимости искомых переменных (обычно зависимость выходных параметров объекта от внутренних и внешних параметров). Графическую модель представляют в виде структурных схем, графов, эквивалентных схем, динамических моделей диаграмм и т.д. Структурная схема может быть приведена в операционной, матричной форме и в виде графов. Матричные структурные схемы и графы применяют при исследовании сложных систем, поэтому в данном пособии не рассмотрены. Подробное описание этих систем и способов их решения даны в [4] и другой технической литературе, посвященной проблеме моделирования. Математическое моделирование можно разделить на два основных метода: метод решения обобщенного дифференциального уравнения системы и структурный метод моделирования. Первый метод в настоящее время используют для моделирования систем уравнений редко. Основными недостатками моделирования по дифференциальным уравнениям являются трудности записи и преобразования нелинейных звеньев. При таком методе моделирования исключена возможность исследования и синтеза различных корректирующих звеньев. Поэтому будем рассматривать только структурный метод моделирования в абсолютных единицах. При моделировании используют компьютеры. Основное отличие цифрового моделирования от аналогового — это использование дискретных форм представления непрерывной информации, что позволяет успешно исследовать с большой точностью количественные и качественные взаимозависимости между элементами сложных динамических систем. При математическом моделировании используют три основных вида моделирования: аналоговое (моделирование на АВМ), имитационное и частотное (моделирование на компьютере). Имитационное моделирование — это искусственный эксперимент, в котором вместо натуральных испытаний с реальным оборудованием проводят опыт на математических моделях. Имитационное моделирование состоит из процесса разработки модели реальной системы и постановки экспериментов с этой моделью для оценки поведения системы либо различных схемных решений, обеспечивающих достижение поставленной цели. Практически при имитационном моделировании определяяют зависимость выходного сигнала от входного (управляющего, внешних возмущений или внутренних сигналов системы). Имитационная модель не несет информацию о характеристиках надежности, особенностях конструктивного исполнения и многих других важных свойствах привода, и в этом отношении является неполной. Она отражает лишь качества, важные с точки зрения имитационного моделирования, а именно, взаимосвязь элементов моделируемого объекта в процессе работы. Частотный метод представляет собой моделирование частотных характеристик. Аналоговое моделирование на АВМ в настоящее время не используется. Моделирование на компьютере можно производить, решая обобщенное дифференциальное уравнение n-го порядка или методом структурных схем, где решают дифференциальные уравнения первого порядка для отдельных звеньев, взаимосвязанных между собой. В зависимости от числа независимых переменных дифференциальные уравнения делят на две группы: • обыкновенные, содержащие одну независимую переменную; • уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называют частными. Решение уравнений в частных производных в данном пособии не приводится. Одним из видов решений дифференциальных уравнений является векторно-матричная форма, когда уравнение я-го порядка заменяют математическим описанием в виде системы п линейных дифференциальных уравнений первого порядка. Расчеты, как правило, производят по структурным схемам или методом детальных структурных схем (ДСС). При моделировании по структурным схемам непрерывных систем с помощью компьютеров в основном применяют два подхода. Первый заключается в использовании численных методов интегрирования дифференциальных уравнений (методы Эйлера, Рунге— Кута и т.д.) Второй подход связан с применением операционных методов, характерная особенность которых состоит в том, что исходят не из дифференциальных уравнений, а из структурной схемы и передаточных функций непрерывной системы. В этом случае заменой оператора р на некоторую функцию от z переходят от непрерывной передаточной функции к дискретной м>(г). При сравнении с численными методами операционные методы имеют ряд преимуществ, например, меньшая сложность программы, что открывает возможности моделирования в реальном масштабе времени. Моделирование на компьютере выполняют в следующей последовательности: • составляют функциональную схему электропривода; • описывают звенья схемы дифференциальными уравнениями; • составляют на основе дифференциальных уравнений передаточные функции в операторном виде; • разрабатывают структурную схему электропривода; • производят расчет параметров цепей и регуляторов схемы; • уточняют структурную схему; • разрабатывают алгоритм (блок-схему) расчета переходного процесса на основании структурной схемы; • составляют таблицу машинных обозначений коэффициентов усиления, постоянных времени и т.д.; • составляют программу или расчетную схему в системе MATLAB; • заносят программу в компьютер; • настраивают программу; • производят расчет переходного процесса; • выполняют анализ расчета переходного процесса. Численные методы решения дифференциальных уравнений Краткое описание методов Существует несколько численных методов решений. Их можно разделить на две группы: методы с обособленными шагами интегрирования (одношаговые методы) и методы со связными шагами интегрирования (многошаговые методы). Среди одношаговых методов наибольшее распространение получили метод Эйлера (метод ломаных), усовершенствованный метод Эйлера—Коши и метод Рунге—Кутта. Наиболее простым методом является метод Эйлера, но он наименее точный. Отличие этих методов наблюдается только при описании интегральных, апериодических, изодромных (пропорционально-интегральных) и дифференциальных звеньев. Для решения обыкновенного дифференциального уравнения необходимо знать зависимую переменную и (или) ее производную при некоторых значениях независимой переменной. Если эти дополнительные условия заданы при одном значении независимой переменной, то такую задачу называют задачей с начальными условиями, или задачей Коши. Часто в задаче Коши в роли независимой переменной выступает время. Метод Эйлера — простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. В этом методе отброшены члены второго порядка и выше. И уравнение принимает следующий вид: у(х0 + h) = у(х0)+Ну(х0), где h — достаточно малое число, называемое шагом интегрирования. Метод Тастина [3] основан на преобразовании функции W(р), выраженной в операционной форме по Карсону—Хевисайду, в некоторую функцию z. Функцию F(z) трактуют как изображение непрерывной функции времени f(t), рассматриваемой в дискретные моменты времени. Замена функции в операторном виде по методу Тастина представляют собой замену оператора р на выражение 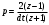 . .В настоящее время для облегчения расчетов созданы специальные математические компьютерные системы, основной из которых является система MAT LAB. Систему MathCAD можно использовать для математического моделирования, а также при решении всевозможных математических задач. По программе MatLAB моделирование можно производить, набирая блоки звеньев структурной схемы с необходимыми ограничениями. В MATLAB — Simulink представлены практически все модели систем управления электроприводом. При расчете по системе MATLAB — Simulink разрабатывать алгоритм и программу не нужно. Необходимо только составить структурную схему и определить значение коэффициентов и постоянных времени передаточных функций, а также время переходного процесса. Моделирование процессов и систем в среде MATLAB Общие сведения о MATLAB В настоящее время для облегчения расчетов созданы специальные математические компьютерные системы: Vigil Basic, MATLAB [1], MATHCAD и др. Особое место среди множества таких систем занимают системы MATLAB и MATHCAD. Они по праву могут называться самыми современными, универсальными и массовыми математическими системами. Назначение этих систем — решение различных вычислительных задач. Система MATLAB [1] принята в качестве официального средства оформления инженерной документации и научных публикаций. Математический аппарат системы MATLAB предельно приближен к современному математическому аппарату инженера и ученого и опирается на вычисления, производимые с матрицами, векторами и комплексными числами. Графическое представление функциональных зависимостей организовано в форме, которую требует инженерная документация. Почти все вычислительные возможности системы можно применять в режиме мощного научного калькулятора, а также составлять собственные программы, предназначенные для многоразового применения. Одной из привлекательных особенностей системы MATLAB является наличие наглядного и эффективного средства составления программных моделей (передаточных функций структурной схемы) — пакета визуального программирования Simulink. С помощью научного калькулятора решают множество задач, от простейших арифметических действий и элементарных действий с комплексными числами до вычисления матричных функций, построения диаграмм и графиков амплиудно-ча- стотных и фазово-частотных характеристик. Пакет Simulink включает в себе библиотеку Browser (Браузер), в которой расположены блоки для составления 5-моделей и систем SimPowerSystems. Принцип составления блок-схемы модели в библиотеке Sim Power Systems [1] существенно отличается от принципа составления блок-схем в 5- моделях. Общая характеристика библиотеки SimPowerSystems Принцип составления блок-схемы модели в библиотеке SimPowerSystems отличается от принципа составления блок-схем в 5-моделях. В последних, соединяемые блоки представляют собой программы математического преобразования входных величин блока в выходные величины независимо от физического содержания, происходящего в них процесса, а линии соединения переносят некоторый информационный сигнал. Соединения же блоков SimPowerSystems следует рассматривать как имитацию электрических соединений, обеспечивающих передачу электрического сигнала (тока) от выхода одного блока к входу другого, а сами блоки — как модели электрических процессов, протекающих в устройстве, поведение которого моделируется. Блоки 5-модели [1] в общем случае не могут быть соединены с блоками библиотеки SimPowerSystems. В технической литературе по MATLAB используют следующую терминологию: 5-блоками называют блоки библиотеки Simulink: Р- блоками — блоки библиотеки SimPowerSystems (SPS); m-линиями — линии, соединяющие 5-блоки; р-линиями — линии, соединяющие Р-блоки. Для связи Р-блоков с обычными 5-блоками предназначены лишь отдельные блоки библиотеки SPS. Среди них измерители электрических сигналов (тока, напряжения и т.п.), /7-входы и т-вы- ходы, ряд блоков источников электрических сигналов, имеющих m-вход и /ьвыходы, а также некоторые другие блоки. Для доступа к библиотеке SPS открывают окно Simulink Library Browser и с помощью контекстного меню библиотеки вызывают окно SimPowerSystems. Анализ основных источников по теме диссертационного исследования 1. Https://cyberleninka.ru/article/n/modelirovanie-perehodnyh-protsessov-v-tortsevom-sinhronnom-generatore-v-pakete-matlab Федий К.С., Встовский С.А., Полошков Н.Е. Моделирование переходных процессов в торцевом синхронном генераторе в пакете Matlab // Журнал Сибирского федерального университета, - 2017. Математическое моделирование в энергетике даже самых простых и широко распространенных устройств ведет к огромной экономии средств и улучшению качества изделий. Чем сложнее проектируемый объект, тем, как правило, важнее роль моделирования в его изучении и создании. Самое широкое применение моделирование находит в механике и физике, электротехнике, радиотехнике и электронике, в технике обработки сигналов и коммуникаций. В статье решена задача исследования переходных процессов в торцевом синхронном генераторе с постоянными магнитами в пакете matlab. Исследованы процессы, возникающие в синхронных машинах при переходных режимах, таких как внезапное короткое замыкание и резкое изменение нагрузки. Процессы, возникающие в синхронных машинах при переходных режимах, например при внезапном коротком замыкании или резком изменении нагрузки, весьма сложны, что вызывает значительные трудности при их точном количественном расчете. Однако поведение синхронной машины при указанных режимах имеет очень большое практическое значение, так как переходные процессы могут вызвать повреждение машины, а следовательно, и значительные убытки, связанные с перерывом энергоснабжения объектов, получающих питание от генератора, или прекращением работы электроприводов с синхронными двигателями. Особенностью математической модели торцевого синхронного генератора с магнитоэлектрическим возбуждением является замена постоянных магнитов на «фиктивную» обмотку возбуждения с включенным в неё источником тока, равным магнитодвижущей силе «фиктивной» коэрцитивной силы. 2. Https://www.elibrary.ru/item.asp?Id=30457182 Глазырин Г.В. Моделирование переходных процессов синхронной машины с несимметрией фазных обмоток статора // Вестник московского энергетического института, - 2017. - № 5 В статье рассмотрены переходные процессы синхронной машины с неодинаковыми индуктивностями и активными сопротивлениями фазных обмоток статора. Появление такой несимметрии возможно при повреждении с謬¬¬нхронной машины, в частности, при межвитковых коротких замыканиях в обмотке статора. Предполагается использование результатов расчетов переходных процессов поврежденной синхронной машины для анализа работы и создания новых алгоритмов релейной защиты генераторов электростанций. Предложен метод численного моделирования переходных процессов синхронной машины с несимметричной обмоткой статора. Метод основан на непосредственном решении дифференциальных уравнений равновесия ЭДС и падений напряжений в обмотках в фазных координатах совместно с уравнением движения ротора. При этом контур каждой фазной обмотки статора описан отдельным уравнением, и могут быть учтены отличающиеся параметры фаз. Разработана и реализована на языке программирования C++ математическая модель синхронного генератора, работающего на активно-индуктивную нагрузку в сети с нулевым проводом, не имеющим сопротивления. Использование подобной схемы позволяет упростить математические выкладки, так как в ней отсутствуют связи между фазными контурами вне синхронной машины. В модели учтен один из возможных видов несимметрии - неодинаковое число витков в фазных обмотках, что позволяет моделировать межвитковые короткие замыкания без учета появления дополнительных короткозамкнутых контуров. Выполнена верификация модели путем сравнения результатов расчета переходных процессов генератора с симметричной обмоткой статора, полученных при использовании разработанной модели и с помощью средств MATLAB Simulink. Проведен анализ результатов моделирования для случая внезапного межвиткового замыкания в обмотке статора гидрогенератора. Полученные результаты позволили сделать вывод об адекватности разработанной модели. 3. Https://cyberleninka.ru/article/n/matematicheskoe-modelirovanie-perehodnyh-protsessov-v-tortsevom-sinhronnom-generatore-s-magnitoelektricheskim-vozbuzhdeniem Архипцев М.Г., Встовский А.Л., Пантелеев В.И., Федий К.С. Математическое моделирование переходных процессов в торцевом синхронном генераторе с магнитоэлектрическим возбуждением // Известия Томского политехнического университета. Инжиниринг георесурсов. – 2012. Разработана математическая модель переходных процессов низкоскоростного торцевого синхронного генератора на методологической основе обобщенного электромеханического преобразователя, для определения параметров которой используется полевая электромагнитная модель исследуемого генератора. 4. Https://www.elibrary.ru/item.asp?Id=41560374 Глазырин Г.В., Митрофанов Н.А. Моделирование переходных процессов в системе генератор-трансформатор –нагрузка с несимметрией фазных контуров статора // Журнал сибирского федерального университета. – 2019.- № 8 Рассматриваются переходные процессы в системе генератор-трансформатор-нагрузка. Предложен метод численного моделирования переходных процессов синхронной машины с возможностью учета несимметрии обмотки статора, появление которой возможно при повреждении синхронной машины, в частности при межвитковых коротких замыканиях в обмотке статора.Метод основан на непосредственном решении дифференциальных уравнений равновесия Э.Д.С. И падений напряжений в обмотках в фазных координатах совместно с уравнением движения ротора. При этом контур каждой фазной обмотки статора описывают отдельным уравнением, и могут быть учтены отличающиеся параметры фаз. Математическая модель реализована в программном пакете MATLAB. В модели учтен один из возможных видов несимметрии - неодинаковое число витков в фазных обмотках, что позволяет моделировать межвитковые короткие замыкания без учета появления дополнительных короткозамкнутых контуров. Выполнена верификация модели посредством сравнения результатов расчета переходных процессов, полученных при использовании разработанной модели и с помощью средств MATLAB Simulink. Проведен анализ результатов моделирования для режимов: холостого хода и нагрузочного режима. Полученные результаты позволили сделать вывод об адекватности реализованной модели. 5. Https://www.elibrary.ru/item.asp?Id=21189922 Встовский А.Л., Архипцев М.Г., Федий К.С. Токи внезапного короткого замыкания в синхронном генераторе с магнитоэлектрическим возбуждением // Журнал сибиского федерального университета – 2013. - №8. В статье представлена математическая модель торцевого синхронного генератора с возбуждением от постоянных магнитов для исследования переходных процессов и влияния токов короткого замыкания на работу машины. 6. Https://cyberleninka.ru/article/n/issledovanie-perehodnyh-protsessov-v-obmotke-rotora-gidrogeneratora-pri-korotkih-zamykaniyah-v-sisteme-s-uchetom-deystviya Расулзода Х.Н., Щедрин В.А. Исследование переходных процессов в обмотке ротора гидрогенератора при коротких замыканиях в системе с учетом действия автоматического регулирования возбуждения // Вестник Чувашского университета. - 2019. В настоящее время исследование режимов работы синхронного генератора параллельно с энергосистемой и повышение их устойчивости являются актуальной задачей. Эффективным средством повышения устойчивости гидрогенераторов служит автоматическое регулирование возбуждения. При расчетах и анализе нормальных установившиеся и переходных режимов электрических систем широко применяется среда моделирования MATLAB/Simulink. Благодаря её возможностям (существующей базе, блокам и моделям), а также с помощью описания элементов управления представляется возможным провести анализ режима работы синхронного гидрогенератора в энергосистеме в условиях различных коротких замыканий с учетом автоматического регулирования возбуждения сильного действия. В статье приведены результаты исследования переходных процессов в обмотке ротора гидрогенератора Нурекской ГЭС. Полученные результаты позволяют провести сравнение переходных процессов в роторе и влияния автоматического регулирования возбуждения сильного действия при различных коротких замыканиях. 7. Https://cyberleninka.ru/article/n/matematicheskaya-model-sinhronnogo-generatora-s-sistemoy-samovozbuzhdeniya-v-rezhime-forsirovki-pri-nesimmetrichnyh-korotkih Горшков К.Е., Гольдштейн М.Е. Математическая модель синхронного генератора с системой самовозбуждения в режиме форсировки при несимметричных коротких замыканиях в энергосистеме // Вестник Южно-Уральского государственного унивеситета. – 2009. Разработана математическая модель синхронного генератора с системой самовозбуждения для анализа электромагнитных процессов в режиме форсировки при внешних несимметричных коротких замыканиях. В модели учитываются группы соединения обмоток трансформатора системы самовозбуждения, способы синхронного фазового управления тиристорным преобразователем и элементы автоматического регулятора возбуждения. Приведены результаты исследований режима форсировки блока ТГВ-200-2М. 8. https://cyberleninka.ru/article/n/perehodnye-protsessy-v-elektricheskih-mashinah-postoyannogo-toka Моисеева Р.Р., Баженов Н.Г., Самигуллина Р.Х., Зацаринная Ю.Н. Переходные процессы в электрических машинах постоянного тока // Вестник Казанского технологического университета. – 2013. В данной статье рассматриваются переходные процессы, происходящие в электрических машинах постоянного тока. При анализе этих процессов делается вывод о том, что скорость этого процесса велика и ток в цепи якоря при пуске превышает номинальный в несколько раз, что может привести к соответствующему нагреву обмотки якоря. 9. https://cyberleninka.ru/article/n/perehodnye-protsessy-v-razvetvlennyh-elektricheskih-setyah Санкин Ю.Н., Пирожков С.Л. Переходные процессы в разветвленных электрических сетях // Вестник Ульяновского государственного технического университета. – 2007. Предложен смешанный вариационный принцип для преобразованных по Лапласу токов и напряжений, учитывающий начальные условия, для разветвленной электрической сети. Разработан метод расчета переходных процессов в сложной электрической сети при подаче напряжения. 10. https://cyberleninka.ru/article/n/modelirovanie-elektromagnitnyh-perehodnyh-protsessov-v-setyah-s-trehfaznymi-silovymi-transformatorami Кузнецов В.В., Каланчин Д.Ю., Антонов Д.Б., Низовой А.Н. Моделирование электромагнитных переходных процессов в сетях с трехфазными силовыми трансформаторами // Вестник Воронежского государственного технического университета. – 2011. 11. https://cyberleninka.ru/article/n/perehodnye-protsessy-v-avtonomnoy-energoustanovke-s-asinhronnym-generatorom Костырев М.Л., Воеводина О.А. Переходные процессы в автономной энергоустановке с асинхронным генератором // Вестник государственного технического университета. Серия: Технические науки. – 2012. В статье рассматривается задача совершенствования автономных энергоустановок с асинхронными генераторами. Предложены математические модели для исследования динамических режимов. Приведены результаты компьютерного моделирования, предложены решения по обеспечению требуемого качества генерируемой электроэнергии. Список Литературы 1. Лазарев Ю. Моделирование процессов и систем в MATLAB, СПб.: издательская группа BHV, 2005 2. Веников В.Л. Теория подобия и моделирования применительно к задачам электроэнергетики. — М.: Высшая школа, 1976. 3. Тарасик В.П. Математическое моделирование технических систем. — Минск: Дизайн ПРО, 1997. 4. Шуп Т.Е. Прикладные численные методы в физике и технике. — М.: Высшая школа, 1990. |
