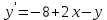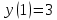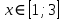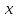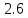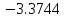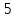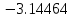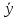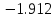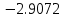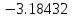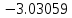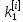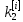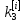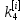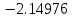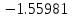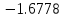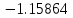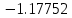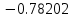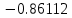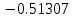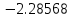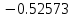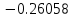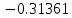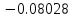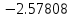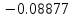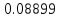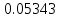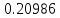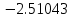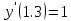Вычислительная математика. Практическое задание 6 Вариант 8. Практическое задание 6. Тема Численные методы решения дифференциальных уравнений и систем Лекция Численные методы решения обыкновенных дифференциальных уравнений и систем первого и второго порядка
 Скачать 33.35 Kb. Скачать 33.35 Kb.
|
Практическое задание 6Тема 6. Численные методы решения дифференциальных уравнений и систем Лекция 6.1. Численные методы решения обыкновенных дифференциальных уравнений и систем первого и второго порядка Номера вариантов задач определяются с помощью табл. 1 по первой букве фамилии студента. Таблица 1
Вариант 8 Задание 6.1. Решить задачу Коши для дифференциального уравнения первого порядка на заданном отрезке: методом Эйлера; модифицированным методом Эйлера; методом Рунге – Кутты.
Решение: 1) Метод Эйлера Метод Эйлера численного решения задачи Коши 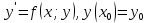 на заданном отрезке с шагом на заданном отрезке с шагом 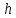 заключается в вычислении значений функции по итерационным формулам: заключается в вычислении значений функции по итерационным формулам: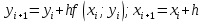 Расчетная формула метода Эйлера: 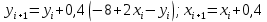 Шаг 1: 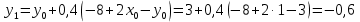 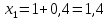 Дальнейшие рассчеты представим в таблице:
Ответ: 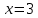 ; ; 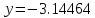 2) Модифицированный метод Эйлера В модифицированном методе Эйлера численного решения задачи Коши 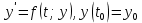 на заданном отрезке с шагом на заданном отрезке с шагом 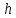 вначале определяется “грубое приближение”: вначале определяется “грубое приближение”: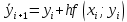 После чего вычисляется приближенное решение: 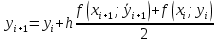 Выполним вычисления по формулам: “грубое” приближение: 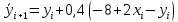 приближенное решение: 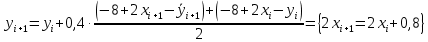 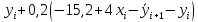 Шаг 1: “грубое” приближение: 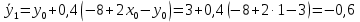 приближенное решение задачи Коши: 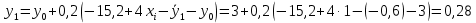 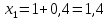 Дальнейшие рассчеты представим в таблице:
Ответ: 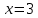 ; ; 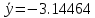 ; ; 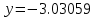 3) метод Рунге-Кутты Решение дифференциального уравнения вида 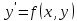 на каждом шаге итерации сроится следующим образом: на каждом шаге итерации сроится следующим образом: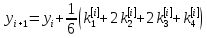 Где коэффициенты вычисляются по формулам: 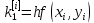 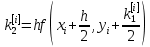 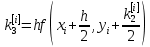  Выполним вычисления по формулам: 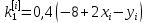 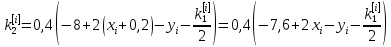 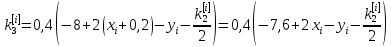 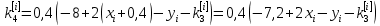 Шаг 1: Вычисляем значения коэффициентов: 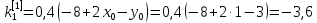 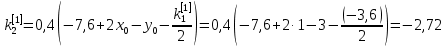 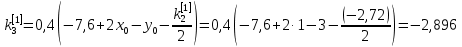 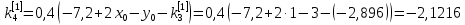 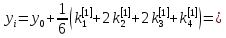 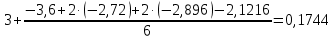 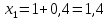 Дальнейшие рассчеты представим в таблице:
Ответ: 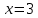 ; ; 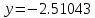 Задание 6.2 1. Найти решение дифференциального уравнения второго порядка с заданными начальными условиями методом неопределенных коэффициентов. 2. Найти первые пять членов решения дифференциального уравнения второго порядка с заданными начальными условиями.
Решение: Используем метод конечных разностей. Произведем дискретизацию области непрерывного аргумента сеткой с шагом 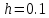 , тогда , тогда 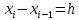 для всех для всех 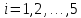 . .Вычислим решение краевой задачи не в произвольных точках отрезка, а только в узлах сетки. Производные 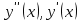 аппроксимируем центральными разностными производными: аппроксимируем центральными разностными производными: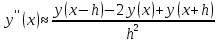 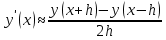 Заменяем в каждом из внутренних узлов 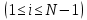 сетки исходное дифференциальное уравнение приближенным равенством: сетки исходное дифференциальное уравнение приближенным равенством: Потребуем теперь, чтобы значения искомой сеточной функции удовлетворяли во всех внутренних узлах сетки уравнениям, полученных заменой знака приближенного равенства на знак строгого равенства: 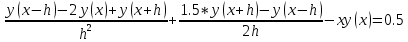 Или: 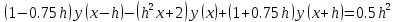 В граничных узлах сеточная функция должна удовлетворять равенствам: 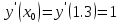 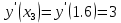 Граничные условия аппроксимируем правой и левой разностной производными: 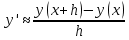 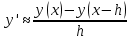 Тогда имеем 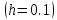 : :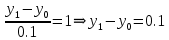 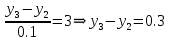 Приводим уравнения для внутренних узлов 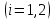 сетки к виду: сетки к виду: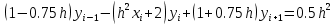 С учетом того, что 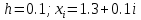 получаем следующую систему уравнений для определения численного решения краевой задачи: получаем следующую систему уравнений для определения численного решения краевой задачи: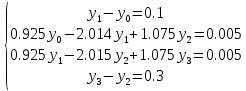 Выражая последовательно: - из первого уравнения: 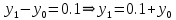 - из второго уравнения: 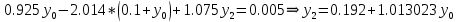 - из четвертого уравнения: 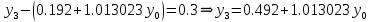 Подставляя в третье уравнение, находим: 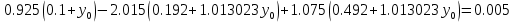 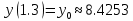 Остальные значения: 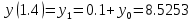 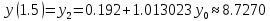  Ответ: 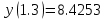 ; ; 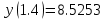 ; ; 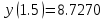 ; ; 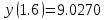 |