Матлаб сам работа. Моделирования регистров

• Название: Моделирования регистров
• Анкор: Матлаб сам работа
• Дата: 20.04.2022
• Размер: 180.89 Kb.
• Имя файла: Matlab_Xamdamov_sam_rabota.docx
• Тип: Документы; #486507

Тема: Моделирования регистров

План:

Введение

1. Определение характеристик входного воздействия во временной области

2. Определение характеристик входного воздействия в частотной области

3. Синтез системы временным методом

4. Синтез системы частотным методом

5. Определение характеристик системы

6. Схемотехническая реализация системы

7. Моделирование системы

8. Анализ функционирования системы

9. Выводы

10. Перечень ссылок

ВВЕДЕНИЕ

Интенсивное развитие компьютерной техники позволяет сегодня снизить затраты времени на оформление различной конструкторской, технологической, проектной и другой технической документации, а также предоставляет возможность моделировать системы и процессы в электронике, механике, гидродинамике, оптике, автоматике и других отраслях знаний.

В настоящее время существует большое количество прикладных программ, среди которых можно выделить графические редакторы, текстовые редакторы, базы данных, программы для различного вида обработки данных и построения графиков, программы для моделирования процессов, программы и пакеты автоматизированного проектирования и конструирования и другие виды программ.

Моделирование различных систем, объектов, процессов, явлений природы и т.д. имеет важное значение в науке и технике. Благодаря моделированию существенно облегчается и удешевляется исследование физических, химических и других природных явлений, технических объектов, создание образцов новой техники. Моделированием называется создание моделей реальных объектов и их экспериментальные исследования. В свою очередь модель - это, как правило, упрощенное отражение реального объекта, несущее те его качества, которые подвергаются исследованию (моделированию). Например, модель вновь создаваемого самолета или ракеты, продуваемые в аэродинамической трубе - это уменьшенные копии реальных летательных аппаратов, идентичные им по конфигурации и геометрически пропорциональные, но не имеющие двигательных установок, систем управления и вооружения. Данная модель позволяет получить картину движения воздушных потоков у фюзеляжа и несущих плоскостей и смоделировать поведение летательного аппарата в полете. Другой пример - модель технологического объекта - печи, реализованный в виде схемы из транзисторов, диодов, резисторов и конденсаторов. Такая модель совсем не похожа на реальное устройство, но она позволяет получить необходимые электрические характеристики, (например фазовые координаты), идентичные настоящей печи и дает возможность синтезировать и отработать систему управления реальным объектом, позволяя экономить время и средства.

Большое значение имеют, также, математические модели. Они позволяют производить моделирование реальных объектов и систем с использованием многочисленных математических методов, оперируя со свойствами объектов, выраженными в виде различных математических зависимостей и соотношений. Например, хорошо известная модель, описывающая силу, действующую на движущееся тело при изменении его скорости - второй закон Ньютона. Или математическая модель взаимодействия двух тел в гравитационном поле - закон всемирного тяготения. Математические модели той или иной степени сложности, как правило, идеализированы и отражают только исследуемые характеристики реальных объектов.

С математическими моделями тесно связаны компьютерные модели, которые в зависимости от программы в которой производится моделирование, используют те или иные математические характеристики реальных объектов. В настоящее время в связи со значительным прогрессом в области компьютерной техники компьютерное моделирование приобрело большое значение в науке и технике. На сегодняшний день существует значительное количество специализированных пакетов, таких как MatLab, MathCad, Math, Mathematica, Maple и др., которые дают широкие возможности для компьютерного моделирования различных процессов и систем.

Целью курсовой работы является приобретение практических навыков решения различных технических задач с использованием компьютерной техники. В частности, необходимо углубить и закрепить знания и опытные навыки работы с системой MatLab, полученные в курсе дисциплины «Компьютерная графика», а также освоить принципы синтеза, анализа и моделирования устройств в системе MatLab и ее пакетах расширения. Необходимо, также, научиться строить графические зависимости функций и сигналов в пакетах расширения MatLab, работать с табличными данными, конвертировать таблицы и графики в текстовый редактор Word и оформлять текстовые документы, включающие в себя формулы, таблицы, графические объекты.

В процессе выполнения курсовой работы по заданному входному воздействию будет синтезирована линейная система, которая согласована по частотному спектру с этим сигналом. Для этого вначале определяются временные и частотные характеристики заданного входного сигнала и строятся графики одиночного импульса, периодической последовательности и спектральной функции. Затем осуществляется синтез системы временным и частотным методом, определяются временные и частотные характеристики синтезированной системы с применением пакета расширения Control System Toolbox и строятся их графики. После этого осуществляется построение функциональной схемы и структурной модели синтезированной системы в Simulink и ее моделирование на различных режимах, в процессе которого должны быть получены графики, отражающие ее работу. На основании этого выполняется анализ функционирования разработанной системы.

. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ВХОДНОГО ВОЗДЕЙСТВИЯ ВО ВРЕМЕННОЙ ОБЛАСТИ

Согласно заданию, входное воздействие представляет собой последовательность треугольных импульсов со скважностью Q = 4. Входной импульс имеет длительность фронта t_ф = 2 нс и амплитуду Um = 98 В.

Принимая момент начала действия импульса t=0 c, можно составить

математическую модель входного сигнала в виде кусочной функции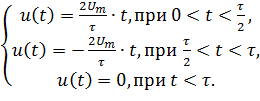

(1.1)

где Um=98В;

τ=4*10^-9 c.

Для удобного аналитического описания сигнала с целью дальнейших преобразований, необходимо перейти к его динамическому представлению посредством функций включения



;

, (1.2)

где σ(t) - функция Хевисайда.

По полученному соотношению (1.2) в Simulink строится структурная схема, приведенная на рисунке 1.1.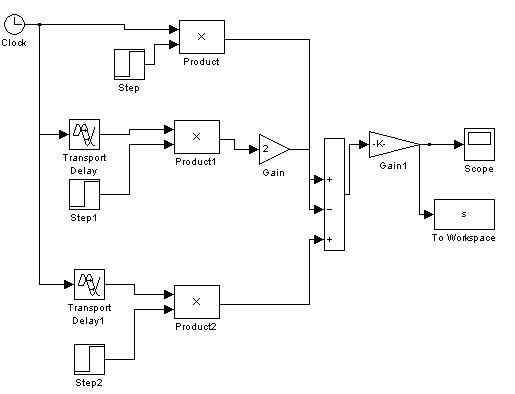



Рисунок 1.1 - Структурная схема для моделирования одиночного импульса входного воздействия

График сигнала, полученный в результате моделирования, показан на рисунке 1.2.

Для получения графика импульсной последовательности с заданными параметрами построена структурная схема, представленная на рисунке 1.3. При заданной длительности импульса и скважности период последовательности определится из соотношения

, (1.3)

нс.

График последовательности импульсов входного воздействия представлен на рисунке 1.4.



Рисунок 1.2 - График одиночного импульса входного воздействия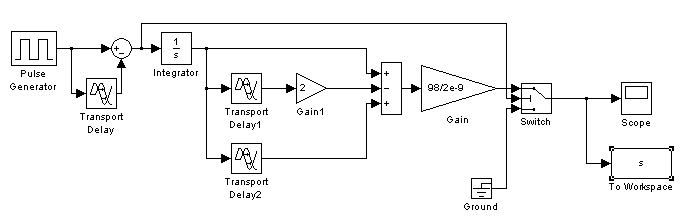



Рисунок 1.3- Структурная схема для моделирования последовательности импульсов входного воздействия



Рисунок 1.4 - График последовательности импульсов входного воздействия

2. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ВХОДНОГО ВОЗДЕЙСТВИЯ В ЧАСТОТНОЙ ОБЛАСТИ

Для получения спектральной плотности сигнала входного воздействия используется прямое преобразование Фурье

(2.1)

Для рассмотренного в первом разделе треугольного импульса

(2.2)



(2.3)

При заданных t_И = 4 нс и U_m = 98 В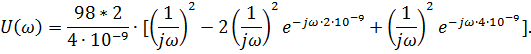



По полученному выражению для спектральной функции сигнала, используя MatLab в режиме научного калькулятора, производится расчет диапазона частот и вектора спектральной плотности. Диапазон частот определяется соотношением

(2.4)

где - верхняя частота диапазона; - длительность импульса.

Для треугольного импульса:

_.

На основании рассчитанных значений строится график, представленный на рисунке 2.1.

Проанализировав полученную зависимость, можно сделать вывод, что входное воздействие имеет непрерывный спектр, и основная часть энергии сосредоточена в окрестности частоты ω=0 рад/с.



Рисунок 2.1 - График спектральной функции сигнала входного воздействия

3. СИНТЕЗ СИСТЕМЫ ВРЕМЕННЫМ МЕТОДОМ

В данном разделе необходимо синтезировать систему, согласованную по частотному спектру с сигналом внешнего воздействия. Синтез системы будет производиться временным методом.

Из теории цепей известно, что если u₁(t) - сигнал на входе линейной системы, а u₂(t) - выходной сигнал, то связь между ними описывается интегралом свертки

(3.1)

где h(t) - импульсная характеристика линейной системы.

У физически реализуемых систем h(t)=0 при t<0, то

(3.2)

Из курса теоретической радиотехники известно, что импульсная характеристика системы, согласованной по частотному спектру с некоторым заданным сигналом , с точностью до постоянного множителя C равна зеркальному (по временной шкале) отображению этого сигнала с некоторым временем запаздывания

(3.3)

Для рассматриваемого треугольного импульса

(3.4)

Искомая импульсная характеристика линейной системы

(3.5)

Если принять

, , (3.6)

то

(3.7)

Таким образом, временным методом найдена импульсная характеристика (3.7) системы, согласованная по частотному спектру с сигналом внешнего воздействия.

4. СИНТЕЗ СИСТЕМЫ ЧАСТОТНЫМ МЕТОДОМ

В данном разделе необходимо синтезировать систему, согласованную по частотному спектру с сигналом внешнего воздействия. Синтез системы будет производиться спектральным методом.

В разделе 2 была найдена спектральная функция треугольного импульса (2.3).

. (4.1)

Из курса теоретической радиотехники известно, что частотная передаточная функция, согласованная с сигналом по спектру системы равна

(4.2)

где U^*(ω) - функция комплексно сопряженная заданному спектру.

Функция, комплексно сопряженная спектральной плотности сигнала входного воздействия

.

Таким образом, согласованная заданному сигналу система имеет частотную передаточную функцию

(4.4)

Если принять

,

То



(4.5)

Для того, чтобы убедиться в эквивалентности синтеза согласованной системы частотным и временным методом, производится обратное преобразование Фурье по отношению к частотному коэффициенту передачи, так как импульсная характеристика связана с частотным коэффициентом передачи обратным преобразованием Фурье

. (4.6)

Для заданного сигнала



(4.7)

Таким образом, спектральным методом получен тот же результат, что и временным.

. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СИСТЕМЫ

В данном разделе необходимо определить временные и частотные характеристики разрабатываемой системы и построить их графики. Для решения поставленной задачи будет использован пакет расширения MatLab - Control System Toolbox.

Для того, чтобы воспользоваться возможностями данного пакета необходимо перейти от частотного коэффициента передачи К(jω) к передаточной функции К(p), которая является аналитическим продолжением К(jω) с мнимой оси jω на всю плоскость комплексных частот p=σ+jω.

(5.1)

Учитывая параметры сигнала (см. раздел 1)

(5.2)

На основании полученной передаточной функции (5.2) рассчитываются АЧХ и ФЧХ и строятся их графики. Для этого передаточной функции (5.2) в Control System Toolbox создается TF-объект. Звено чистого запаздывания представляется передаточной функцией, полученной в результате разложения этого звена в ряд Паде (в Matlab существует встроенная процедура разложения звена чистого запаздывания в ряд Паде). Последовательность процедур для решения поставленной задачи представлена ниже. Результаты выполнения этой последовательности представлены на рисунках 5.2 - 5.9.

i=tf(1,[1 0]);

[num,den]=pade(2e-9,2);=tf([num],[den]);

[num,den]= pade(4e-9,2);=tf([num],[den]);=(i^2)*(1-2*z1+z2);=pole(p)=zero(p)=0:1e+7:2e+10;=j*w;

[num,den]=tfdata(p,'v');=polyval(num,kw);=polyval(den,kw);=abs(ch./zn);=angle(ch./zn)*180/pi;(1);(w,ACH,'k');;('w, rad/s');('U,B');(2);(w,FCH,'k');;('w, rad/s');('Fi,degr');(3)(p,'k');;(4)(p,'k');;(5)(p,'k');;(6)(p,'k');;(7)(p,'k');;(8)(p,'k');;



Рисунок 5.2 - График АЧХ разрабатываемой системы



Рисунок 5.3 - График ФЧХ разрабатываемой системы



Рисунок 5.4 - График переходной характеристики разрабатываемой системы



Рисунок 5.5 - График импульсной характеристики разрабатываемой системы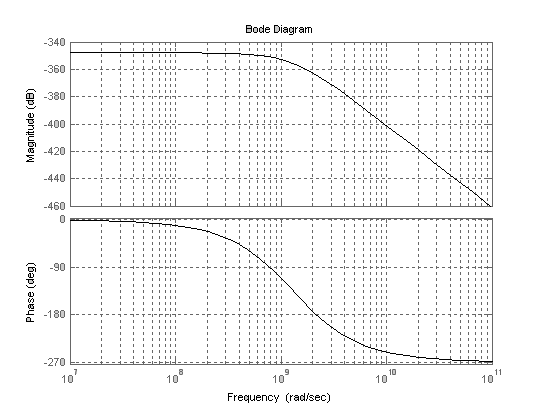



Рисунок 5.6 - Графики ЛАЧХ и ЛФЧХ разрабатываемой системы



Рисунок 5.7 - График амплитудно-фазовой характеристики
разрабатываемой системы



Рисунок 5.8 - График Николса разрабатываемой системы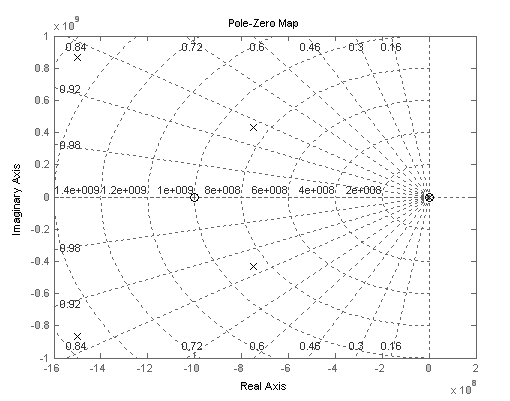



Рисунок 5.9 - Карта полюсов и нулей разрабатываемой системы

. СХЕМОТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ СИСТЕМЫ

В данном разделе необходимо разработать функциональную схему и структурную модель синтезированного устройства в Simulink.

В разделах 3 и 4 были получены импульсная характеристика и частотная передаточная функция разрабатываемого устройства и показано, что описание устройства этими функциями носит эквивалентный характер. Таким образом, для построения функциональной схемы можно воспользоваться выражением для частотной передаточной функции (4.4)





Из данного уравнения видно, что устройство состоит из интегратора, линии задержки и сумматора, включенных как показано на рисунке 6.1.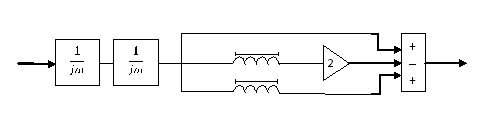



Рисунок 6.1 - Схема функциональная согласованной системы для треугольного импульса

Теперь, выбирая соответствующие блоки из библиотеки Simulink, на основании полученной функциональной схемы строится структурная модель, приведенная на рисунке 6.2.



Рисунок 6.2 - Схема структурная модели согласованной системы для треугольного импульса

частотный передаточный помеха временной

7. МОДЕЛИРОВАНИЕ СИСТЕМЫ

С целью анализа функционирования системы необходимо произвести моделирование разработанной схемы в пакете расширения Simulink.

Для оценки искажений, вносимых разработанным устройством в выходной сигнал при прохождении импульса, с которым система согласована по спектру, производится моделирование схемы при действии одиночного импульса и отсутствии помехи. Графики входного и выходного сигнала при действии одиночного импульса приведены на рисунках 7.1, 7.2.

Для оценки искажений, вносимых разработанным устройством в выходной сигнал и степени релаксации схемы при действии импульсной последовательности, производится моделирование схемы при воздействии последовательности импульсов с заданной скважностью и отсутствии помехи. Графики входного и выходного сигнала при действии помехи приведены на рисунках 7.3, 7.4.

Для оценки воздействия согласованной системы на помеху производится моделирование схемы при действии только сигнала помехи. В качестве помехи выбирается гармоническая функция, имеющая такую же амплитуду, как и у заданного сигнала входного воздействия. Частота сигнала помехи определяется из графика амплитудно-частотной характеристики оптимальной системы (рис.5.1) на уровне 0,01 от максимального значения АЧХ. Для рассматриваемого примера параметры сигнала помехи: Um=98B, ω=0,8∙10¹⁰ рад/с. Графики входного и выходного сигнала при действии помехи приведены на рисунках 7.5, 7.6.

Для оценки степени подавления помехи и эффективности работы системы производится моделирование схемы при действии аддитивной смеси сигнала и помехи. В качестве входного сигнала используется импульсная последовательность. Графики входного и выходного сигнала при действии помехи приведены на рисунках 7.7, 7.8.



Рисунок 7.1 - График входного сигнала разработанной системы при действии одиночного импульса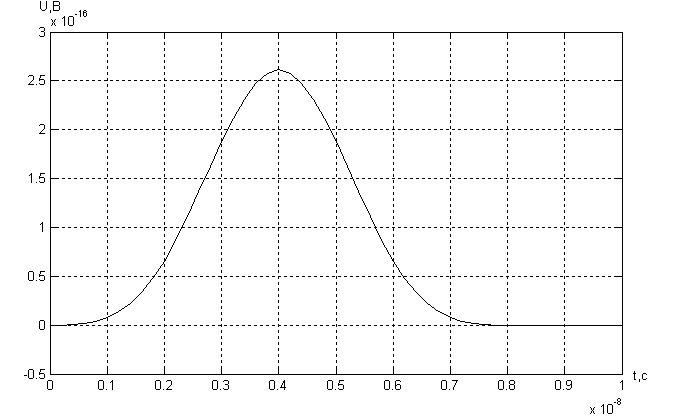



Рисунок 7.2 - График выходного сигнала разработанной системы при действии одиночного импульса



Рисунок 7.3 - График входного сигнала разработанной системы при действии последовательности импульсов



Рисунок 7.4 - График выходного сигнала разработанной системы при действии последовательности



Рисунок 7.5 - График входного сигнала разработанной системы при действии помехи



Рисунок 7.6 - График выходного сигнала разработанной системы при действии помехи



Рисунок 7.7 - График входного сигнала разработанной системы при действии сигнала и помехи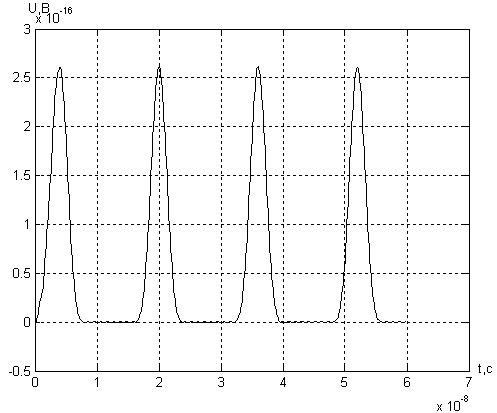



Рисунок 7.8 - График выходного сигнала разработанной системы при действии сигнала и помехи

8. АНАЛИЗ ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ

Анализируя функциональную и принципиальную схемы разработанного устройства, а также характеристики, полученные в разделе 5, можно сделать вывод, что данное устройство представляет собой фильтр нижних частот с полосой прозрачности Δω=10⁹ рад/с.

Анализируя графики работы разработанного устройства при одиночном импульсном воздействии (рис. 7.1, 7.2), можно сделать вывод, что система изменяет форму входного импульса. То есть такая система является оптимальной спектру входного сигнала по максимуму отношения сигнал/шум .

Анализируя графики работы разработанного устройства при воздействии импульсной последовательности (рис. 7.3, 7.4), можно сделать вывод, что система не вносит заметных искажений в выходные импульсы, что свидетельствует о нормальной релаксации схемы и согласованности по спектру с заданным сигналом.

Анализируя графики работы разработанного устройства при воздействии помехи (рис. 7.5, 7.6), можно сделать вывод, что система вносит значительное затухание в выходной сигнал. Графические зависимости показывают, что отношение амплитуд входного и выходного сигнала составляют около 26*10^-17.

Анализируя графики работы разработанного устройства при воздействии аддитивной смеси импульсной последовательности и сигнала помехи (рис. 7.7 - 7.8), можно сделать вывод, что разработанное устройство эффективно подавляет сигнал помехи и выделяет без заметных искажений полезный сигнал на фоне помех. Отношение сигнал/шум определенное по графику 7,8 составляет 260. Это свидетельствует о согласованности разработанной системы по спектру с заданным сигналом внешнего воздействия и ее оптимальности по критерию максимума отношения сигнал/шум.

ВЫВОДЫ

В результате выполнения курсового проекта разработана система, согласованная по спектру с заданным сигналом входного воздействия - треугольным импульсом.

В процессе анализа входного сигнала были получены графики одиночного импульса и импульсной последовательности, представленные на рис. 1.2 и рис. 1.4. Спектральная плотность сигнала имеет ярко выраженный максимум при нулевой частоте. Проанализировав полученную зависимость, можно сделать вывод, что входное воздействие имеет непрерывный спектр, и основная часть энергии сосредоточена в окрестности частоты ω=0 рад/с.

Был произведен синтез системы согласованной по частотному спектру с сигналом внешнего воздействия временным и частотным методом. Определены ее характеристики и получены их графики. На основании выражения для частотного коэффициента передачи синтезирована функциональная схема (рис. 6.1), и структура для моделирования системы в Simulink (рис. 6.2).

Анализируя функциональную схему разработанного устройства, а также характеристики, полученные в разделе 5, можно сделать вывод, что данная система представляет собой фильтр нижних частот с полосой прозрачности Δω=10⁹ рад/с.

Анализируя графики работы системы (рис.7.1-7.8) можно сделать вывод, что разработанное устройство изменяет форму входного импульса. При воздействии импульсной последовательности разработанное устройство не вносит заметных искажений в выходные импульсы, что свидетельствует о нормальной релаксации схемы и согласованности системы по спектру с заданным сигналом. В то же время устройство вносит значительное затухание в гармонический сигнал, являющийся помехой.

Анализируя графики работы системы при воздействии аддитивной смеси полезного сигнала и сигнала помехи, можно сделать вывод, что разработанное устройство эффективно подавляет помеху и выделяет без заметных искажений полезный сигнал на фоне помех. Отношение сигнал/шум составляет 260. Это свидетельствует о согласованности разработанного устройства по спектру с заданным сигналом внешнего воздействия. Таким образом, разработанная система является оптимальной по критерию максимума отношения сигнал/шум.

В процессе выполнения курсового проекта были закреплены знания и навыки, полученные в курсе «Компьютерная графика». Усовершенствованы практические навыки работы с текстовым редактором Word и системой MatLab. Освоены принципы синтеза, анализа и моделирования устройств в этой системе и ее пакетах расширения - Simulink, Control System Toolbox.

Полученные знания и навыки будут использованы в дальнейшем при изучении других дисциплин, выполнении курсовых проектов и дипломной работы, а также в будущей инженерной и научной деятельности.

ПЕРЕЧЕНЬ ССЫЛОК

1. Баскаков С.И. Радиотехнические цепи и сигналы. 2-е изд., перераб. и доп. - М.: Высшая школа, 1988. - 448с.

. Айзинов М.М. Радиотехнические цепи и сигналы. - М.: Транспорт, 1966. - 512с.

. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. 2-е изд., перераб. и доп. - Л.: Энергия, 1972. - 816с.

. Лёзин Ю.С. Введение в теорию и технику радиотехнических систем. учеб. пособ. для ВУЗов. - М.: Радио и связь, 1988. - 280с.

. Лёзин Ю.С. Оптимальные фильтры и накопители импульсных сигналов: 2-е изд., перераб. и доп. - М.: Советское радио, 1969. - 448с.

. Ицхоки Я.С., Овчинников Н.И. Импульсные и цифровые устройства. - М.: Советское радио, 1972. - 592с.

. Л.М. Гольденберг. Теория и расчет импульсных устройств на полупроводниковых приборах. - М.: Связь, 1969. - 756с.

. Л. А. Меерович, Л.Г. Зеличенко. Импульсная техника. - М.: Советское радио, 1953. - 832с.

. Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. - СПб.: КОРОНА принт, 1999. - 288 с.

. Потемкин В.Г. Система инженерных и научных расчетов MATLAB 5.х: в 2-х томах. Том 1. - М.: ДИАЛОГ МИФИ, 1999. - 366с.