Модуль і. Основи інформаційних технологій в системі охорони здоров'Я. Обробка та аналіз медикобюлогічних даних

• Название: Модуль і. Основи інформаційних технологій в системі охорони здоров'Я. Обробка та аналіз медикобюлогічних даних
• Дата: 13.02.2023
• Размер: 5.89 Mb.
• Имя файла: medinfo_ocr_recognized.doc
• Тип: Документы; #935067
• страница: 41 из 65

Погарифнпческая Пі


С аленная ^споненцнагъная Лннетая фкиътрацдо

Построен на рядг;

Назватг атрокнтируюшвй (сглаженной) кривой

; ПйгцпОталтм (ПР4ІСТ пасепечіЯ (и* 1000 Ч

352. 
     
     
     
     
     1. 
        пермдсв
        
     2. 
        пврпдс»
        
     
     
     

впврадмні |о цазадна: \О

П пар9:віченне кргеон с осью 1 в точке: 0

О тмена

Р ис. 53. Вкладки діалогового вікна Линия тренда

В результаті отримуємо апроксимуючу криву (рис. 54).

П риріст населення (на 1О&0 чоп.)

нвевлвння (на 1000 чол.)}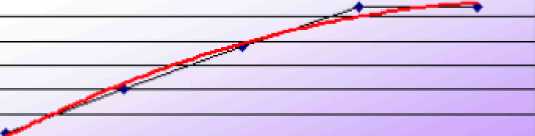

■>»

19.S

19 18,5

18 17,5

17 16.5

16 15,5

_І

Роки

у = -0,1357х- + 1,504 Дї + 15,66 R'= 0,9864

Р ис. 54. Експериментальні дані, апроксіімовані паліноміальнаю кривою

Як видно з рисунка 54, рівняння поліном і альної апроксимуючої функції для деяких значень х (1, 2, З_т...} має вигляду = -0,1357х^:+І,5043х+І5,66. При цьому точність апроксимації досить висока R² = 0,986.

Спробуємо покращити якість апроксимації вибором іншого типу функції (можливо, більш адекватного). В даному випадку допустимим варіантом може бути логарифмічна функція. Для цього аналогічно до описаного вище апроксимуємо дані логарифмічною кривою (тип лінії тренду -Логарифмическая). В результаті маємо інший варіант апроксимації (рис. 55).

108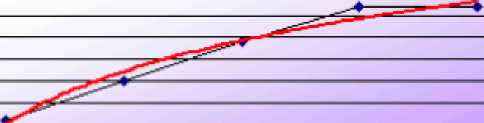

20.5 -

20 19,5

19 18,5

11 -17,5 ■

17 ■ 16,5

16 15,5

■ Приріст населення (на 1000 чол.)

•Логарифмический (Прчркт щеплення (на 1000 чол.))

Роки У = 1,7493Ln(x;i + 17,005

R'= 0,9716

Р ис. 55. Експериментальні дані, апроксимовані логарифмічною кривою

Проаналізувавши рисунок 55, стверджуємо, що рівняння логарифмічної апроксимуючої кривої поступається в точності апроксимації поліноміальної кривої R² = 0,9716 < 0,986. Тому, за відсутності будь - яких теоретичних міркувань, можна вважати, що найкращою апроксимацією є апроксимація поліноміальною функцією другого степеня (з двох розглянутих варіантів).

Демонстраційний приклад 2

Після викиду я довитої речовини його концентрація (мг/л) у водоймищі змінювалась у відповідності з наступною таблицею:

Час після викиду (і од.)	]	3	5	8
Концентрація речонини (mi/jj)	8,0		J,o	0,3

Визначимо тип функціональної залежності зміни концентрації речовини з часом і оцінимо її концентрацію в момент викиду. Для цього введемо дані в електронну таблицю та побудуємо діаграму. Оскільки необхідно будувати динаміку зміни концентрації речовини відповідно з вказаними проміжками часу (нерівномірними) - будуємо діаграму Точечная (рис. 56).

Апроксимуємо отриману криву. Оскільки крива візуально походить на експоненту і з теоретичних міркувань ймовірніше, що закон зміни -експоненціальний, доцільно апроксимувати криву зміни концентрації експоненціальною функцією. Дія цього викликаємо контекстне меню графіка, в якому вибираємо пункт Добавить линию тренда. В діалоговому вікні, що з'явилося, Лінія тренда на вкладці Тип вибираємо тип лінії тренда Експоненціальна. Потім відкриваємо вкладку Параметры і встановлюємо прапорці в поля показывать уравнения на диаграмме та поместить на диаграмму величину достоверности аппроксимации (R^A2). Крім цього, для того щоб оцінити концентрацію речовини у водоймищі в момент викиду, в полі Прогноз назад на встановлюємо / периодов. Після чого натискаємо кнопку ОК. В результаті отримуємо апроксимуючу криву (рис. 57).

109

Як видно з рисунка 57, рівняння експонентної апроксимуючої функції для залежності концентрації від часу має вигляд у = 11,844е° ⁹⁵. При цьому точність апроксимації досить висока R² = 0,9951', що дозволяє вважати опис процесу зміни концентрації речовини у водоймищі експоненціальною функцією адекватним. Розрахункова оцінка концентрації речовини в момент викиду, як видно з графіка, становить близько 12 мг/л. Точнішу цифру отримуємо з рівняння у =