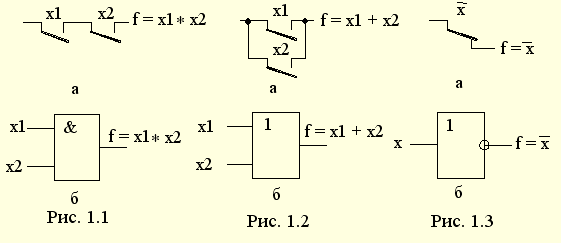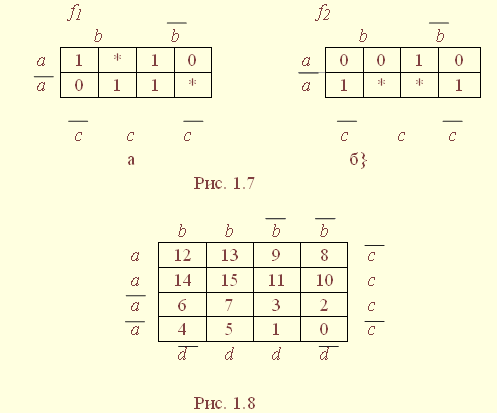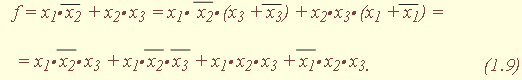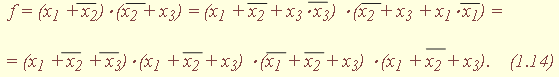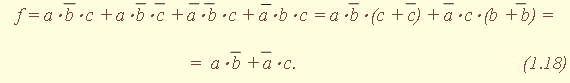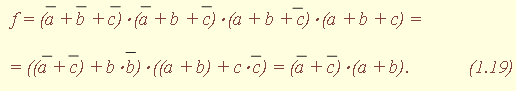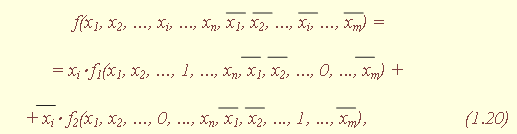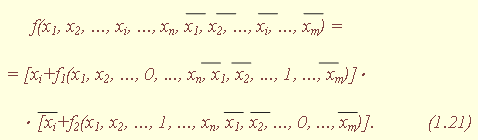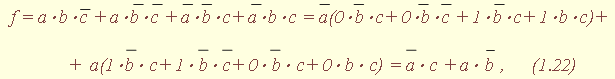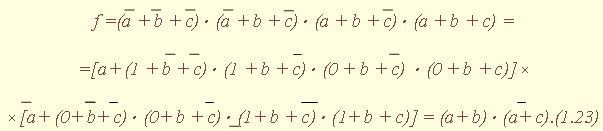курсовая пример. Мой шифр 01076 преобразование логических функций
 Скачать 0.5 Mb.
|
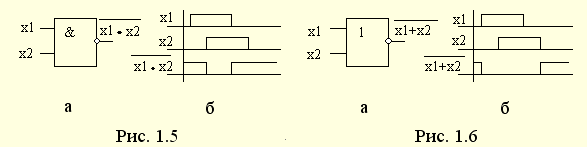
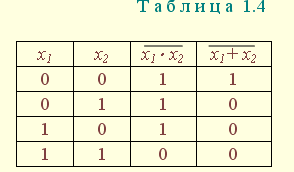
", , или " * ", а при числовом способе задания не полностью определенной функции указываются множества наборов, на которых ФАЛ принимает значения 1 (обязательные номера), и наборов, на которых функция равна 0 (запрещенные номера) или ее значения не определены (условные номера): |
(табл. 1.7) могут быть представлены картами Карно (рис. 1.7):
, где xi – недостающий аргумент:
, полученные в соответствии с законом склеивания, составляется импликантная таблица (табл. 1.8), по которой проводятся операции поглощения в соответствии с [4], и записывается минимизированная функция. Для функции, записанной в СКНФ,
, а импликантная таблица составляется в виде табл. 1.9.
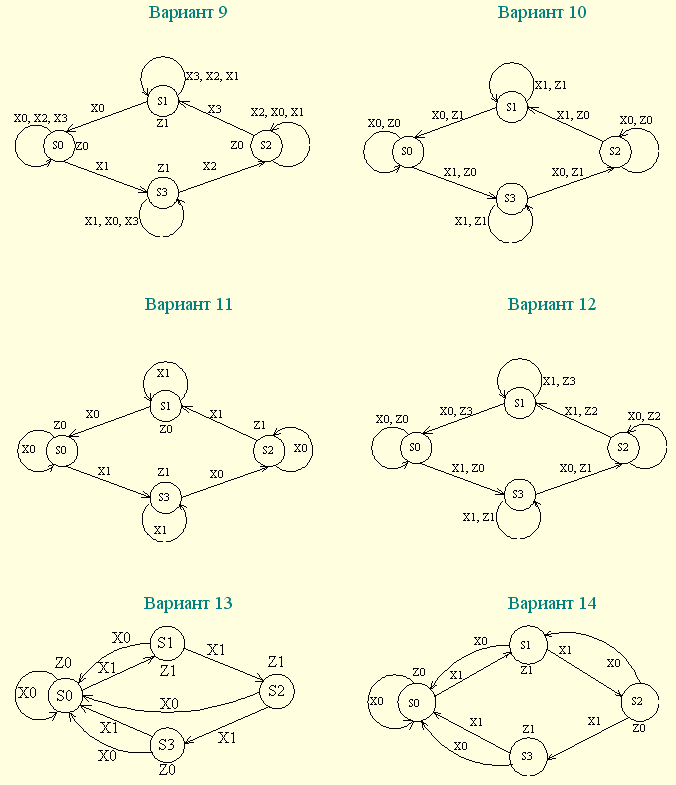
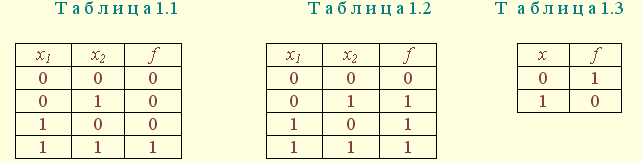
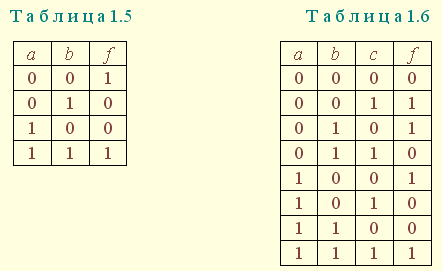
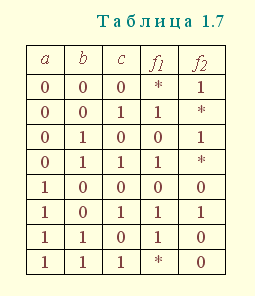
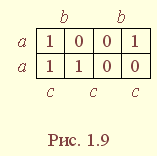
| 1.5. Задания к разделу 1 Вариант задания выбирается из табл. 10 в соответствии с порядковым номером в журнале или по заданию преподавателя. Для студентов заочного отделения вариант выбирается по сумме цифр шифра, если она не превышает 26. В противном случае – по сумме двух последних цифр.  В соответствии с заданием требуется: 1) представить заданную функцию таблицей истинности, СДНФ, СКНФ, координатным способом; 2) минимизировать функцию методами: алгебраическим, Карно, Квайна; 3) записать минимизированные функции в МДНФ и МКНФ; 4) обосновать применяемые методы с точки зрения законов алгебры логики и дать их сравнительные характеристики; 5) сделать выводы о целесообразности применения того или иного метода при различных формах ФАЛ; 6) составить задачу и решить ее наиболее рациональным методом 2. СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ 2.1. Синтез комбинационных схем на релейно-контактных элементах На релейно-контактных элементах реализуются функции, записанные в базисе {И, ИЛИ, НЕ} в МДНФ и МКНФ, причем прямое значение аргумента представляется замыкающим (фронтовым) контактом, инверсное– размыкающим (тыловым), произведение (конъюнкция) аргументов– последовательным, а сумма (дизъюнкция) – параллельным соединением контактов. Релейно-контактная схема должна иметь столько входов, сколько аргументов содержится в выражении функции. На входах схемы включаются воспринимающие реле, контакты которых осуществляют физическую реализацию ФАЛ. 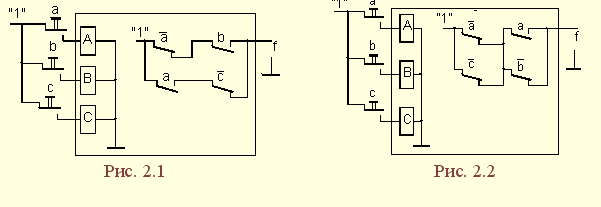 На рис. 2.1 приведена схема, реализующая функцию  а на рис. 2.2 – функцию  Поскольку в каждой из функций содержится по три аргумента, то в схемах, реализующих эти функции, включены по три воспринимающих реле (А, Б, С). Подача входных сигналов осуществляется при нажатии (замыкании) соответствующих кнопок, что вызывает включение того или иного реле. Выходная функция формируется контактами реле в соответствии с выражениями (2.1), (2.2). 2.2. Синтез комбинационных схем на логических элементах базиса {И, ИЛИ, НЕ} К логическим элементам (ЛЭ) данного базиса относятся элементы И – конъюнктор (схема логического умножения, или схема совпадения), ИЛИ – дизъюнктор (схема логического сложения), НЕ – инвертор (схема логического отрицания). На них может быть реализована любая, сколь угодно сложная логическая функция, записанная в соответствующем базисе. Применяя элементы, приведенные в подразделе 2.1, выражения ФАЛ могут быть реализованы схемами, представленными на рис. 2.3 и 2.4. При этом схема, приведенная на рис. 2.3, реализует функцию (2.1), а на рис. 2.4 – функцию (2.2). 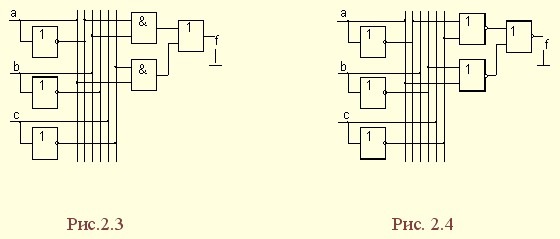 Поскольку в выражениях функций имеются кроме прямых и инверсные значения аргументов, то для их получения в схемах включены инверторы, а сами функции формируются при помощи логических элементов И, ИЛИ. Принципиальные схемы ЛЭ рассмотрены в [1, 2, 4]. Задавая комбинации значений входных сигналов a, b, с согласно таблице истинности (см. табл. 1.6), представленной в подразделе 1.2, получим соответствующие значения выходной функции f. 2.3. Синтез комбинационных схем на логических элементах базиса {ИЛИ, НЕ} К логическим элементам данного базиса относятся элементы Вебба (ИЛИ-НЕ). На них удобно реализовывать ФАЛ, записанные в КНФ. Для приведения КНФ к базису {ИЛИ, НЕ} функция дважды инвертируется и записывается в выражениях Вебба, а затем реализуется на ЛЭ ИЛИ-НЕ. Так, МКНФ функции (2.2)  приводится к базису {ИЛИ, НЕ} следующим образом: При инвертировании функции используется правило де Моргана. Схема, реализующая данное выражение, приведена на рис. 2.5. 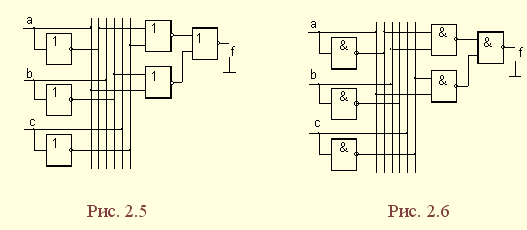 2.4. Синтез комбинационных схем на логических элементах базиса {И, НЕ} К ЛЭ базиса {И, НЕ} относятся элементы Шеффера (И-НЕ). На элементах этого типа удобно реализовать ФАЛ, записанные в ДНФ. Для приведения ДНФ к базису {И, НЕ} функция дважды инвертируется и записывается в выражениях Шеффера, а затем реализуется на ЛЭ И-НЕ. Так, функцию  можно привести к базису {И, НЕ} следующим образом: Схема, реализующая данную функцию, приведена на рис. 2.6. Операции приведения функций алгебры логики к базисам {И, НЕ} и {ИЛИ, НЕ} основаны на законе двойного инвертирования Первая инверсия проводится с целью преобразования выражения ФАЛ таким образом, чтобы оно содержало только те операции, которые реализуются с помощью логических элементов выбранного базиса. Вторая инверсия применяется для того, чтобы сохранить физический смысл функции при записи её в новом базисе. Как видно из примеров, операция инвертирования проводится только один раз, вторая инверсия остаётся нераскрытой. 2.5. Задания к разделу 2 Варианты заданий приведены в табл. 2.1.  Выбор варианта производится согласно указаниям, данным в разд. 1 В соответствии с заданием требуется: 1) минимизировать заданную функцию любым методом; 2) записать МДНФ и МКНФ функции; 3) реализовать ФАЛ на релейно-контактных элементах; 4) реализовать функции на ЛЭ всех базисов. 3. СИНТЕЗ СПЕЦИАЛЬНЫХ КОМБИНАЦИОННЫХ СХЕМ 3.1. Синтез схем с несколькими выходами Комбинационные схемы с несколькими выходами могут быть заданы в виде системы ФАЛ или таблицей истинности. Минимизация функций может проводиться всеми известными методами, но следует учитывать, что при не полностью определенных функциях удобнее использовать метод Карно, а в тех случаях, когда функции определены на всех наборах аргументов и их количество превышает четыре или пять, целесообразно использвать метод Квайна, при котором можно получить наиболее оптимальную схему, в которой одни и те же элементы используются для формирования нескольких ФАЛ. Сущность метода изложена в [ 3, 4]. Пример минимизации методом Квайна рассмотрим при составлении комбинационной схемы, реализующей систему функций: 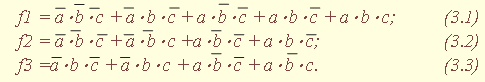 На первом этапе минимизации сведем в табл. 3.1 и 3.2 члены СДНФ (конституенты) и найденные импликанты с указанием функций, содержащих названные элементы. Следующим этапом является составление импликантной таблицы (табл. 3.3) и проведение операций поглощения с целью получения функций в МДНФ. В первую очередь в состав ФАЛ вводятся импликанты, составляющие ядро функции, т. е. перекрывающие столбцы таблицы в единственном числе. Затем записываются импликанты, перекрывающие наибольшее количество столбцов, и в последнюю очередь в состав функций включаются оставшиеся не поглощенными конституенты. Используя правила записи минимальных ФАЛ при методе Квайна, получим:  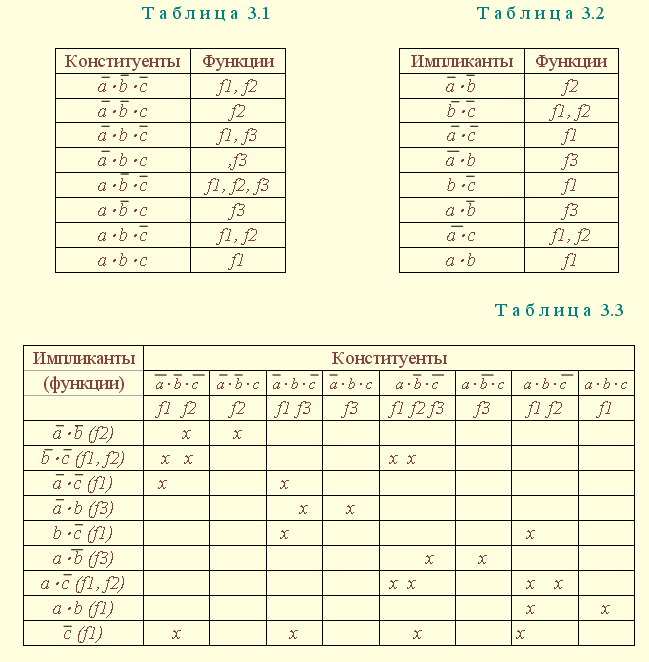 Схемы, реализующие системы функций, составляются по изложенным ранее правилам, и на рис. 3.1 приведен пример реализации полученной системы ФАЛ в базисе {И, ИЛИ, НЕ}. При использовании метода Карно для каждой функции составляется координатная карта и проводятся операции склеивания, в результате кото-рых записываются минимальные выражения ФАЛ. В табл. 3.3 представлен метод минимизации функций алгебры логики в СДНФ, но аналогично минимизируются и системы функций алгебры логики в СКНФ (см. табл. 1.9). Метод Квайна является основным при минимизации логических функций с помощью ЭВМ. 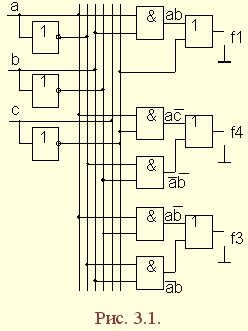 3.2. Синтез шифратора двоичного кода Шифратор (кодер) предназначен для кодирования десятичных цифр двоичным кодом и представляет собой комбинационную схему, имеющую 10 входов и количество выходов, соответствующее числу разрядов кода. Двоичные коды, при помощи которых представляются десятичные цифры в устройствах автоматики, связи и вычислительной техники, приведены в табл. 3.4. Определяющей характеристикой каждого кода является его основание, представляющее вес каждого разряда кода или способ его образования. При известном основании кода легко осуществить перевод числа, записанного в двоичной форме, в десятичное. Для этого достаточно каждый двоичный разряд числа заменить значением его веса и провести сложение всех разрядов. Исключение составляют коды с избыточностью, когда каждой десятичной цифре искусственно присваивается определённая кодовая комбинация.  Рассмотрим пример синтеза шифратора кода 8421. Условное обозначение шифратора приведено на рис. 3.2. Таблица истинности (табл. 3.5) для шифратора 8421 составлена в соответствии с таблицей кодов и представляет собой таблицу четырёх ФАЛ (x1 , x2 , x3 , x4 ) от десяти аргументов (y0 , y1 , y2 ,.. y9 ). 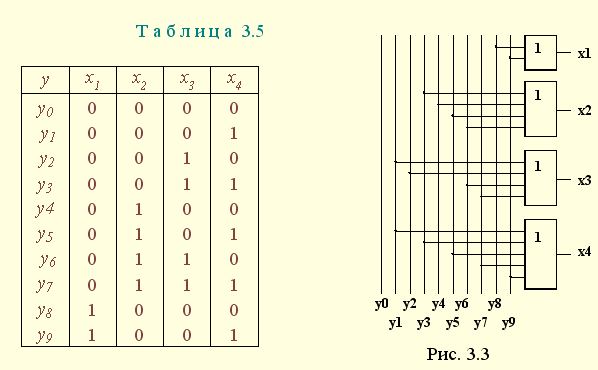 Выражения логических функций для выходов шифратора: 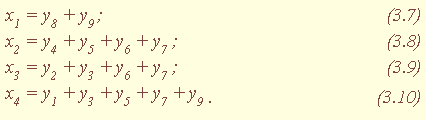 Таким образом, получается система уравнений, представляющая собой математическую модель комбинационной системы, которую можно реализовать на любой элементной базе и, в частности, на логических эле-ментах ИЛИ (рис. 3.3). 3.3. Синтез дешифратора двоичного кода Дешифратор (декодер) преобразует двоичный код в десятичное число. Условное обозначение декодера кода 8421 показано на рис. 3.4. Декодер имеет количество входов, соответствующее разрядности дешифри-руемого кода, и десять выходов по числу десятичных цифр. 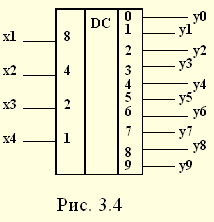 При поступлении на входы дешифратора кодовой комбинации сигналов на одном из его выходов, номер которого соответствует этой комбинации, появляется уровень логической единицы. Таблица истинности дешифратора аналогична табл. 3.5 за исключением того, что функциями будут y0 , y1 , y2 ,.. y9, а аргументами x1 , x2 , x3 , x4. Выражения для выходов дешифратора также записываются в виде системы ФАЛ:  которая может быть реализована на любой элементной базе. В частности, удобно такой дешифратор выполнить на логических элементах ИЛИ-НЕ, для чего необходимо дважды проинвертировать все функции и получить выражения Вебба: 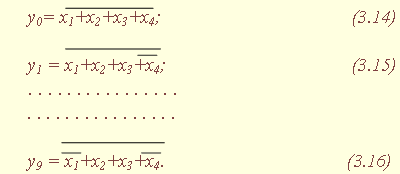 Схема, составленная в соответствии с приведенными выражениями, показана на рис. 3.5. 3.4. Синтез преобразователя двоичного кода Преобразователи кодов предназначены для преобразования одного двоичного кода в другой. Синтез преобразователя кода (ПК) может осу-ществляться двумя способами. При первом способе ПК составляется из дешифратора и шифратора в соответствии со структурной схемой, приве-денной на рис. 3.6. 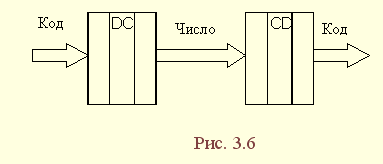 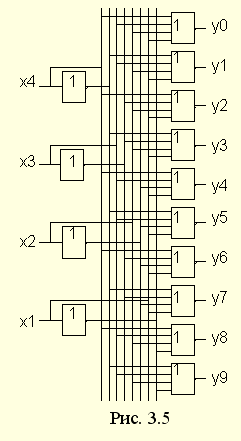 Следовательно, задача в этом случае заключается в соединении дешифратора и шифратора в одну схему. При втором способе ПК составляется, как комбинационная схема с количеством входов, равным разрядности преобразуемого, и числом выходов, равным количеству разрядов нового кода. Таблица истинности для ПК составляется аналогично табл. 3.4. В качестве аргументов служат значения разрядов преобразуемого, а функциями являются разряды нового кода. В табл. 3.6 приведено соответствие между входами и выходами преобразователя кода 8421 в код 2 из 5. Минимизированные формы логических функций для выходов ПК получаются с помощью метода Карно, при котором для каждой ФАЛ составляется координатная карта и проводятся операции склеивания. Так, выражение для y1 можно получить, если заполнить карту Карно так, как показано на рис. 3.7. 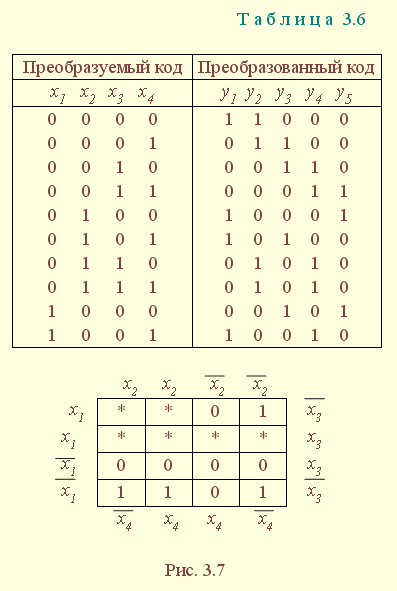 Проведя операции склеивания, получим 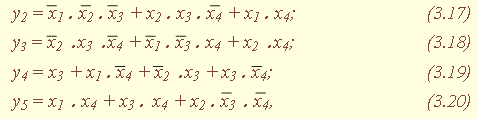 Аналогично заполняются карты для всех остальных функций и получаются их выражения в МДНФ или МКНФ: исходя из которых составляется схема преобразователя кода. 3.5. Задания к разделу 3 З а д а н и е 1 Минимизировать методом Квайна систему ФАЛ и реализовать ее на релейно-контактных и логических элементах базисов {И, ИЛИ, НЕ}, {И, НЕ}, {ИЛИ, НЕ}. 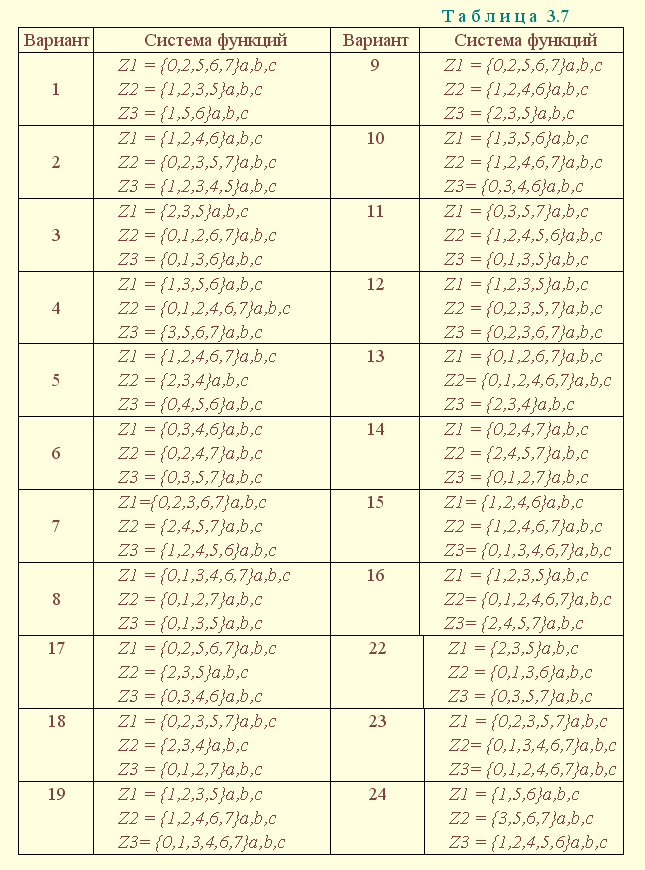 З а д а н и е 2  П р и м е ч а н и е. Схемы шифраторов, дешифраторов и преобразователей кодов составить на элементах Шеффера и Вебба. 4. СИНТЕЗ КОНЕЧНОГО АВТОМАТА 4.1. Способы задания конечных автоматов Конечный автомат может быть задан словесным алгоритмом, таблицами переходов (ТП) и выходов (ТВ), графом состояний и системой уравнений, выражающих зависимости между входами, выходами и внутренними состояниями автомата. Последний (алгебраический) способ задания представляет собой математическую модель, по которой составляется схема, реализующая заданный алгоритм. Следовательно, в любом случае конечной формой задания автомата является алгебраическая, а порядок синтеза сводится к получению математической модели и функциональной схемы автомата и состоит из следующих этапов: 1) составление словесного алгоритма работы автомата; 2) определение числа состояний автомата; 3) составление таблиц переходов и выходов; 4) определение количества элементов памяти автомата; 5) кодирование таблиц переходов и выходов; 6) составление таблицы истинности конечного автомата; 7) получение математической модели автомата; 8) составление функциональной схемы; 9) составление принципиальной схемы. |
4.2. Синтез асинхронного конечного автомата
4.2.1. Кодирование асинхронного автомата
При синтезе асинхронного автомата необходимо решить вопрос исключения критических состязаний элементов памяти (ЭП). Наиболее распространенными способами, предполагающими исключение критических состязаний в процессе синтеза, являются методы кодирования таблиц переходов таким образом, чтобы при функционировании автомат не смог оказаться в незаданных по условиям переходов состояниях. Универсальным является метод кодирования ТП по столбцам [2], использование которого рассмотрим на примере синтеза автомата, заданного ТП (табл. 4.1) и ТВ (табл. 4.2). При этом метода вводится понятие -класса, представляющего собой множество, включающее устойчивое и все неустойчивые состояния, из которых заданы переходы в данное устойчивое состояние. Критические состояния возникают в том случае, когда схема в результате состязаний ЭП попадает вместо одного устойчивого состояния в другое, т. е. из одного -класса схема ошибочно перейдёт в другой. Для исключения этого явления вводятся переменные, разделяющие классы внутри каждого столбца ТП. Они имеют одинаковое значение в кодах состояний одного -класса и различное для кодов состояний других -классов. Для разделения состояний внутри одного -класса вводятся дополнительные переменные, которые одновременно являются разделяющими для -классов другого столбца.
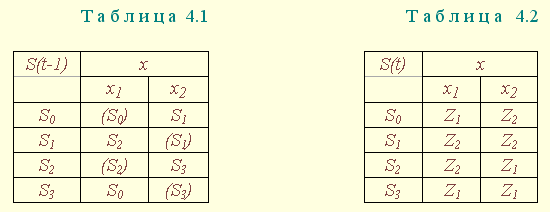
Согласно используемому методу для первого столбца ТП (табл. 4.1)
, а для второго
, где в скобках указаны номера строк с устойчивыми и неустойчивыми состоя-ниями. Необходимое количество элементов памяти определится по формуле:
Таким образом, для реализации автомата требуется два элемента памяти (Y1 и Y2), причём Y1 предназначен для разделения -классов первого столбца, Y2 - второго (табл. 4.3), а состояния автомата закодируются согласно табл. 4.4.
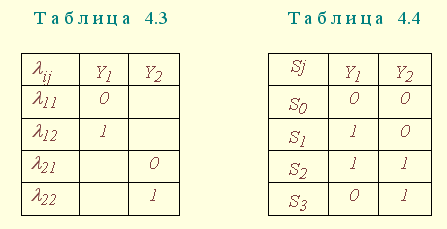
Кодированные ТП и ТВ представляются в виде табл. 4.5 и 4.6 соответственно.
В некоторых случаях, при большем количестве состояний автомата, при кодировании ТП появляются дополнительные (промежуточные) состояния, которые используются для исключения критических состязаний. Подробное описание метода изложено в [2]. Рассмотрим пример кодирования таблицы переходов (табл. 4.7), содержащей основные и дополнительные состояния. Основными являются те состояния, в которые схема автомата должна приходить в соответствии с заданием, а дополнительными - те, в которых схема может оказаться вследствие неодновременного срабатывания ЭП. Как видно из табл. 4.7, переходы из дополнительных состояний заданы таким образом, что в случае состязаний элементов памяти схема не сможет перейти из одного -класса в другой, поскольку из всех основных и дополнительных состояний любого -класса переходы заданы в устойчивое состояние этого класса.
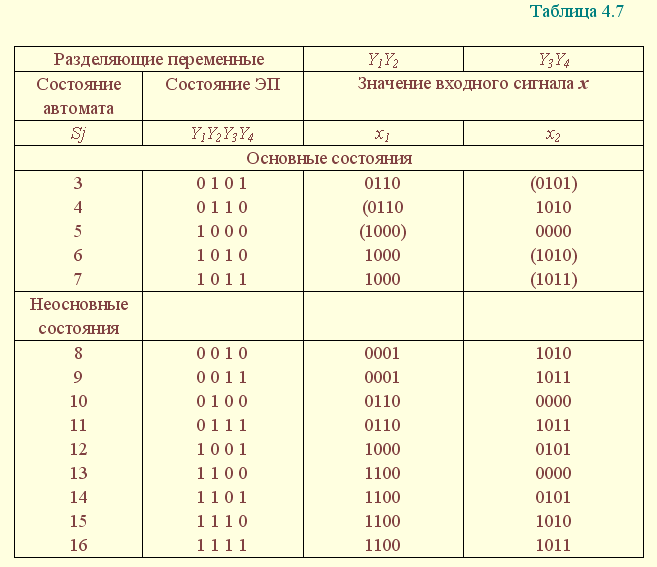
4.2.2. Синтез релейно-контактного автомата
Схема релейно-контактного автомата составляется на основании таблицы истинности (табл. 4.8).
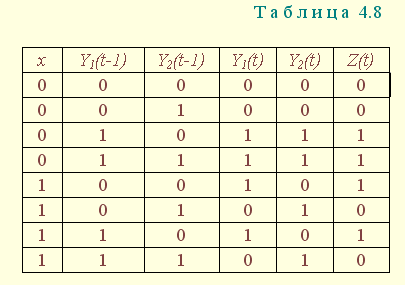
Таблица истинности формируется из таблиц переходов и выходов (см. табл. 4.5 и 4.6). Функциями в этих таблицах являются Y1(t), Y2(t), Z(t), а x, Y1(t -1), Y2(t -1) - аргументами указанных функций, причем Y1(t), Y2(t) представляют собой значения внутренних состояний, Z(t) - выходов, x - входа в настоящий момент времени, а Y1(t -1), Y2(t -1) - значения внутренних состояний в предыдущий момент. Математическая модель автомата представляется системой уравнений, полученных с помощью рассмотренных ранее методов:
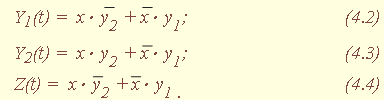
Схема релейноконтактного автомата, составленная в соответствии с его математической моделью, приведена на рис. 4.1.
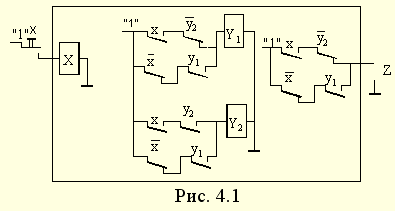
На этой схеме реле Х является воспринимающим, реле У1 и У1 - элементами памяти, реализованной с помощью обратных связей (цепей самоблокировки). Функции управления ЭП и выхода формируются контактами указанных реле.
4.2.3. Синтез автомата на бесконтактных элементах
В асинхронных автоматах на бесконтактных элементах в качестве ЭП используются RS-триггеры. В отличие от релейноконтактных при синтезе бесконтактных конечных автоматов необходимо получить выражения для функций управления S- и R-входами триггеров. Поэтому ТП автомата на RS-триггерах содержит столбцы для S и R функций, в которые записаны значения входных сигналов, переводящих триггеры из одного состояния в другое. Уровни этих сигналов определяются в соответствии с таблицей переходов триггера (табл. 4.9), в которой Y1(t-1) и Y2(t-1) – состояния прямых выходов триггера в предыдущий, а Y1(t) и Y2(t) – в настоящий момент времени. S1, R1 и S2 , R2– управляющие сигналы, переводящие триггеры из предыдущего состояния в настоящее.
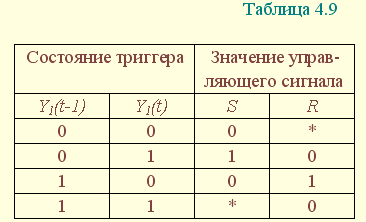
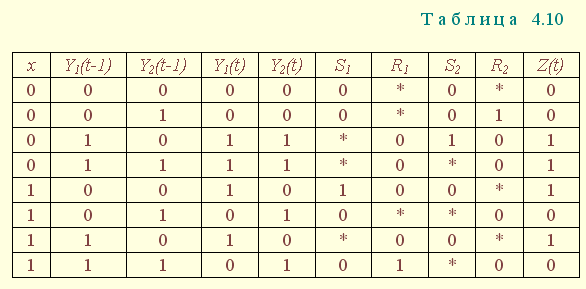
Таблица истинности асинхронного автомата представлена табл. 4.10.
Математическая модель автомата представляется системой функций:
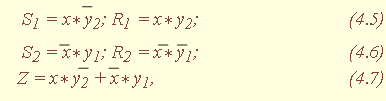
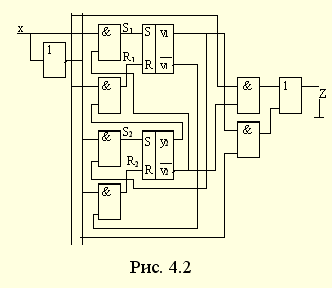
а схема автомата, составленная на основании его математического описа-ния, приведена на рис. 4.2.
4.3. Синтез синхронного автомата
В синхронных автоматах в качестве ЭП используются триггеры с синхронизирующими входами. Синхронизация работы функциональных узлов автомата является одним из способов исключения критических состязаний элементов памяти, поскольку синхронизирующие импульсы подаются через интервалы времени, в течение которых завершаются переходные процессы и все элементы системы приходят в устойчивое состояние. Следовательно, при синтезе синхронного автомата ТП кодируется произвольно. Так, таблица переходов (см. табл. 4.1) в отличие от табл. 4.5 представлена кодированной таблицей (табл. 4.11), в которой состояния закодированы двоичными числами, соответствующими порядковым номерам состояний, а таблица выходов представляется табл. 4.12.
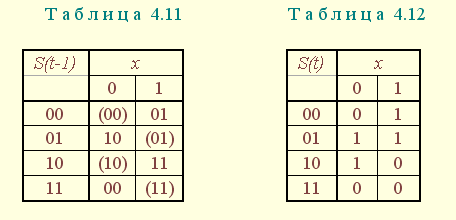
Таблица истинности (табл. 4.13), составленная по ТП и ТВ, учитывает то, что в качестве ЭП выбраны JK- триггеры, принципы управления которыми представлены в табл. 4.14.
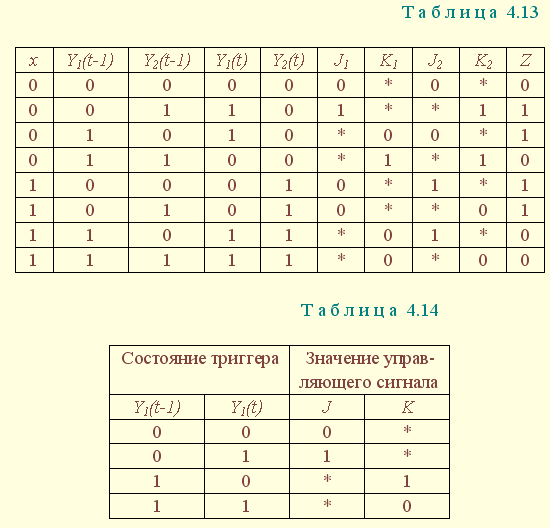
Математическое описание конечного автомата на JK-триггерах представляется системой функций, полученных из табл. 4.13 методом Карно:
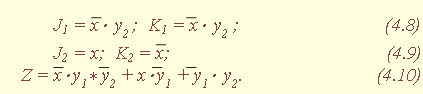
Схема синхронного автомата приведена на рис. 4.3.
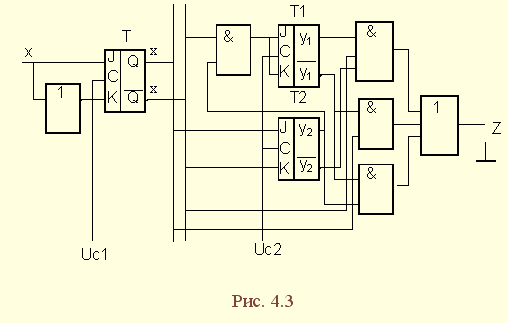
Синхронизация входа автомата осуществляется импульсами напряжения Uc1, подаваемыми на синхронизирующий вход триггера Т, а блока памяти – импульсами Uc2, которые подаются на синхронизирующие входы триггеров Т1 и Т2, выполняющих функции элементов памяти. Изменение состояния триггеров возможно только при поступлении синхронизирующих импульсов, подаваемых в те моменты времени, когда все переходные процессы в схеме заканчиваются.
Таким образом повышается устойчивость работы автомата.
4.4. Задания к разделу 4
В соответствии с номером варианта составить схемы автоматов, представленных в задании графами, на релейно-контактных элементах, RS- и JK-триггерах. Порядок выполнения задания следующий.
1. В соответствии с графом составить таблицы переходов и выходов.
2. Определить необходимое количество элементов памяти.
3. Закодировать состояния автомата с учётом исключения критиче-ских состязаний элементов памяти.
4. Составить кодированные таблицы переходов и выходов.
5. Составить таблицы истинности для автоматов на релейно-контактных и бесконтактных элементах.
6. Записать функции управления и выходов автомата.
7. Составить функциональные схемы автоматов на релейно-контактных и бесконтактных элементах.
