Сборник самостоятельных работ. московский колледж бизнестехнологий
 Скачать 281.08 Kb. Скачать 281.08 Kb.
|
Самостоятельная работа. Эквивалентные и эффективные ставкиЦель работы - научиться проводить расчеты по замене ставок и условий финансовых контрактов, используя формулы финансовых вычислений; сравнивать эффективность различных финансовых операций.  Основные формулы re=(1 + r/m)m – 1 (5.1) re=e - 1 (5.2)  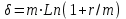 (5.3) (5.3)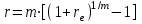 (5.4) (5.4)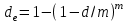 (5.5) (5.5)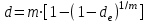 (5.6) (5.6)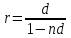 (5.7) (5.7)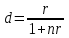 (5.8) (5.8)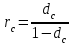 (5.9) (5.9)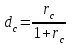 (5.10) (5.10)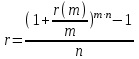 (5.11) (5.11)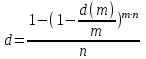 (5.12) где (5.12) где 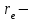 эффективная ставка, эффективная ставка,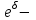 сила роста, сила роста,r - простая процентная ставка, d - простая учетная ставка, rс - сложная ссудная ставка, dс – сложная учетная ставка, r(m ) -сложная процентная ставка с начислением процентов m раз за период, d(m) -сложная учетная ставка с начислением процентов m раз за период, n - продолжительность финансовой операции в годах Контрольные вопросы Какая ставка называется эффективной? От каких параметров она зависит? Как изменяется эффективная ставка с ростом количества начислений сложных процентов в году? В каком случае эффективная ссудная ставка совпадает с номинальной? Какие ставки называются эквивалентными? Типовые задачи с решениями Задача 1. Cрок уплаты по долговому обязательству – полгода, простая учетная ставка – 18% годовых . Какова доходность этой операции, измеренная в виде простой ставки ссудного процента? Решение По формуле (5.7) при d=0,18; n=0,5 r = 0,18 / (1-0,50,18) =0, 198. Доходность операции, выраженная в виде простой ставки ссудного процента, равна 19,8% годовых. Задача 2. Определить номинальную ставку, если эффективная ставка равна 9 % и сложные проценты начисляются ежемесячно. Решение. По формуле (5.4) при r(e) =0,09; m=12 r = 12 [(1 + 0,09)1/12 - 1 ] = 0,086 Таким образом, ежегодное начисление сложных процентов по ставке 9% годовых дает тот же результат, что и ежемесячное начисление сложных процентов по ставке 8,6 %. Задачи для самостоятельной работы. Задача 1. Определить номинальную учетную ставку, если годовая эффективная учетная ставка равна 20% годовых и учет осуществляется 1) каждые полгода; 2) ежеквартально; 3) ежемесячно. Задача 2. Ссуда выдана при условии начисления сложных процентов по ставке 8 % годовых. Определить эквивалентную простую ставку при сроке ссуды 5 лет, 180 дней, 365 дней. Задача 3. Банком выдан кредит на 9 месяцев под 24% годовых с ежеквартальным начислением сложных процентов. Определите величину простой учетной ставки, обеспечивающей такую же величину начисленных процентов. Самостоятельная работа. Замена и консолидация платежей.Цель работы - научиться проводить расчеты по замене ставок и условий финансовых контрактов, используя формулы финансовых вычислений и электронные таблицы EXCEL.  Основные формулы Рассмотрим ситуацию, когда платеж Р1 со сроком уплаты n1 заменяется на платеж Р0 со сроком уплаты n0 Простые ссудные ставки Формула для нахождения величины нового платежа при использовании простой ссудной ставки: 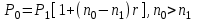 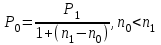 Формула для нахождения срока нового платежа, если 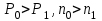 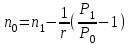 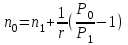 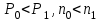 Формула для нахождения срока нового платежа, если Формула для определения величины консолидированного платежа при использовании простой ссудной ставки 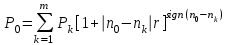 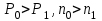 Формула для определения срока консолидированного платежа при использовании простых ссудных ставок 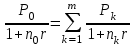 Сложные ссудные ставки Формула для нахождения величины нового платежа при использовании сложной ссудной ставки: 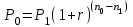 Формула для нахождения срока нового платежа 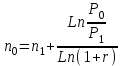 Формула для определения величины консолидированного платежа 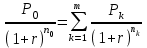 Формула для определения срока консолидированного платежа 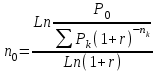 Контрольные вопросы Что означает консолидация платежей? Верно ли утверждение: при сравнении платежей их приведение к одному моменту времени может осуществляться как путем наращения, так и путем дисконтирования? При изменении сроков платежей в каком случае новый платеж будет больше старого платежа, а каком случае меньше? Какие контракты являются эквивалентными? Какие задачи могут возникать при консолидации платежей? Типовые задачи с решениями Задача 1. Согласно новому финансовому соглашению платеж в 100000 руб. со сроком уплаты через 1 год заменяется платежом со сроками уплаты 1) через полгода; 2) через два года. Определить величину нового платежа, если используется простая ставка 20 % годовых. Решение 1) Так как срок нового платежа меньше года, то его величина — это дисконтированная стоимость 100000 руб., срок дисконтирования — 0,5 года, поэтому величина нового платежа равна: 100 000 / (1 + 0,5 ·0,2) = 90 909 руб. 2) Так как срок нового платежа больше года, то его величина — это будущая стоимость 100000 руб., наращение происходит один год по ставке 20 % годовых, поэтому величина нового платежа равна: 100 000 · (1+1·0,2)= 120 000 руб. Задача 2. Два векселя номинальной стоимостью 20000 руб. и 30000 руб. и сроком погашения 1 июня и 1 сентября заменяются одним с продлением срока погашения до 1 октября. При объединении используется простая учетная ставка 10 % годовых. Определить номинальную стоимость нового векселя. Решение Поскольку срок погашения нового векселя позже, чем сроки погашения объединяемых векселей, то на сумму 20000 руб. в течение 122 дней (с 1 июня по 1 октября) происходит наращение капитала по простой учетной ставке 10 %; на сумму 30000 руб. в течение 30 дней (с 1 сентября по 1 октября) также происходит наращение капитала по простой учетной ставке 10 % годовых. Поэтому номинальная стоимость нового векселя равна: 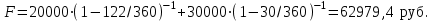 Задачи для самостоятельной работы. Задача 1. В банк для учета предъявлены 2 векселя - один на сумму в 100 тыс. руб. и сроком погашения через год, второй – на сумму 150 тыс. руб. и сроком погашения через 2 года. Два векселя необходимо заменить одним, на сумму 250 тыс. руб. Определить срок погашения нового векселя при использовании сложной учетной ставки 20% годовых. Задача 2. Платежи на сумму 300 000 руб., 400 000 руб. и 400 000 руб. должны быть внесены через три месяца, полгода и 9 месяцев соответственно. Достигнуто соглашение о замене этих платежей на один, равный им по сумме. Определить срок нового платежа, если используется простая ссудная ставка 15 % годовых. Задача 3. Согласно контракту, предприниматель должен выплатить кредитору 10 тыс. руб. через год, 40 тыс. руб. через три года и 30 тыс. руб. через 5 лет. Предприниматель предлагает выплатить 30 тыс. руб. через 2 года и 40 тыс. руб. через 4 года. Являются ли эти контракты эквивалентными, если в расчетах используется простая процентная ставка 34% годовых? Задача 4. Три платежа: 10 000 долл., срок погашения 15 мая; 20 000 долл., срок погашения 15 июня; 15 000 долл., срок погашения 15 августа заменяется одним платежом со сроком погашения 1 августа на основе простой процентной ставки. Определить сумму нового платежа. Самостоятельная работа. Начисление процентов в условиях инфляции. Ц  ель работы - научиться рассчитывать доходность финансовых операций в условиях инфляции, используя формулы финансовых вычислений. ель работы - научиться рассчитывать доходность финансовых операций в условиях инфляции, используя формулы финансовых вычислений. Основные формулы Индекс инфляции 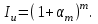 (7.1) (7.1) 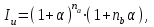 (7.2) (7.2) где 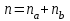 , , 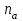 — целое число лет, — целое число лет, 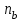 — оставшаяся нецелая часть года — оставшаяся нецелая часть годаВведем следующие обозначения для брутто-ставок: rα —простая ссудная ; dα—простая учетная rсα—сложная ссудная dсα—сложная учетная Вычисление брутто-ставки процентов в условиях инфляции 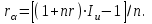 (7.3) (7.3)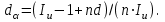 (7.4) (7.4)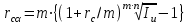 (7.5) (7.5)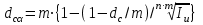 (7.6) (7.6)Формулы для вычисления реальной доходности финансовой операции, когда задан уровень инфляции и брутто ставка 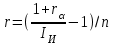 (7.7) 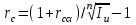 (7.8) Контрольные вопросы Как определяется и что характеризует темп инфляции? Почему в условиях инфляции необходимо различать номинальную и реальную процентную ставки? Может ли реальная процентная ставка быть отрицательной? Что определяет формула Фишера? Типовые задачи с решениями Задача 1. Номинальная процентная ставка, компенсирующая действие инфляции, равна 52% годовых. Определите полугодовую инфляцию, если начисление сложных процентов осуществляется каждый квартал. Решение Приравняем годовой индекс инфляции к множителю наращения за год. Полагая 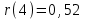 , получим : , получим :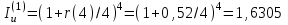 Поэтому индекс инфляции за полгода (0,5 года) составит : 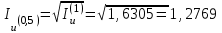 Темп инфляции α находим из условия 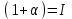 . .Темп инфляции за полгода равен 27,69%. Задача 2. Кредит на сумму 120 тыс.руб. выдается сроком на 3 года при условии начисления сложных ссудных процентов. Индекс цен за указанный период равен 2,5. Какова должна быть процентная ставка по кредиту, чтобы реальная доходность кредитной операции составляла 10% годовых? Рассчитайте сумму к погашению с учетом инфляции. Решение По формуле (7.5) при m=1; r=0,1;I=2,5;n=3 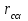 =0,4923 =0,4923Поэтому ставка 49,23% при ежегодном начислении сложных процентов и индексе цен 2,5 обеспечит реальную доходность кредитора 10% годовых. Сумму к погашению с учетом инфляции находим по формуле (3.1) (Занятие 3) при n=3; r=0,4923;P=121 F=120(1+0,4923)3 =399,3 Сумма к погашению с учетом инфляции равна 399 300 руб. Задачи для самостоятельной работы. Задача 1. На вклад в течение 18 месяцев начисляются проценты а) по схеме сложных процентов; б) по смешанной схеме. Какова должна быть годовая процентная ставка, при которой происходит реальное наращение капитала, если каждый квартал цены увеличиваются на 2 %? Задача 2. На некоторую сумму, помещенную на депозит в банк, в течение 8 лет будут начисляться непрерывные проценты. По прогнозам инфляция в это время каждый год будет составлять 1%. Какова должна быть сила роста за год, чтобы сумма вклада через восемь лет по своей покупательной способности не уменьшилась? Задача 3. На вклад в 500 тыс. руб. каждый квартал начисляются сложные проценты по номинальной годовой процентной ставке 4%. Оцените сумму вклада через 3 года с точки зрения покупательной способности, если ожидаемый темп инфляции –1 % за квартал. |
