Сборник самостоятельных работ. московский колледж бизнестехнологий
 Скачать 281.08 Kb. Скачать 281.08 Kb.
|
Самостоятельная работа. Простые ссудные ставки.Цель работы - научиться проводить расчеты по схеме простых ссудных процентов, используя формулы финансовых вычислений.  Основные формулы 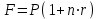 (1.1) (1.1)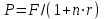 (1.2) (1.2)F=P∙(1+rt /T) (1.3) 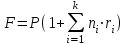 (1.4) (1.4)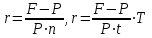 (1.5) (1.5)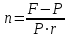 (1.6) (1.6)где P - вложенная сумма; F– наращенная сумма; n - количество периодов продолжительности финансовой операции; r- простая ссудная ставка; Контрольные вопросы Что показывает множитель наращения в формуле наращения простыми процентами? Как связаны между собой наращение простыми процентами и арифметическая прогрессия? В чем заключается различие между точным и приближенным процентом? Что показывает множитель дисконтирования в формуле наращения простыми процентами? Если простую процентную ставку увеличить в два раза, как наращенная сумма? Типовые задачи с решениями Задача 1. Вы поместили в банк вклад 100 тыс. руб. под простую процентную ставку 6% годовых. Какая сумма будет на счете через 3 года? Какова величина начисленных процентов? Решение По формуле (1.1.) при Р=100 тыс. руб., n=3, r =0,06 получаем : F=100 (1+30,06)=118 тыс. руб. Через три года на счете накопится 118 тыс. рублей. Величина начисленных за три года процентов составит: 118 -100=18 тыс. руб Задача 2. Ссуда в сумме 3000 долл. предоставлена 16 января с погашением через 9 месяцев под 25 % годовых (год не високосный). Рассчитайте сумму к погашению при различных способах начисления процентов : а) обыкновенный процент с точным числом дней; б) обыкновенный процент с приближенным числом дней; в) точный процент с точным числом дней . Решение а) По формуле (1.3), используя обыкновенный процент с точным числом дней, рассчитанным по финансовым таблицам (t=289-16=273 дня), получим: F=3000∙(1+0,25273/360=3568,75 долл. Сумма к погашению равна 3568,75 долл. б) По формуле (1.3), используя обыкновенный процент с приближенным числом дней, рассчитанным по финансовым таблицам (t=930=270 дня),получим: F=3000∙ (1+0,25270/360)=3562,5 долл. Сумма к погашению равна 3562,5 долл. в) По формуле (1.3), используя точный процент с точным числом дней, рассчитанным по финансовым таблицам (t=289-16=273 дня), получим: F=3000∙ (1+0,25273/365)=3560,96 долл. Сумма к погашению равна 3560,96 долл. Задачи для самостоятельной работы. Задача 1. Вкладчик внес в банк 20 тыс. руб. Через год он снял со счета половину набежавших за год процентов. Оставшаяся сумма еще год оставалась в банке, на конец года на счете осталось 26,4 тыс. руб. Какую простую ссудную ставку использовал банк? Задача 2. Предприниматель взял в банке ссуду на два года под процентную ставку 32% годовых. Определите, во сколько раз сумма долга к концу срока ссуды будет больше выданной банком суммы, если банк начисляет простые проценты. Задача 3. Предприятию необходим кредит в 10 млн. руб. на полгода. В банке А предлагают следующие условия: процентная ставка за первый месяц -10%, на следующие 3 месяца- 11% и на последние 2 месяца – 14%. В банке В предлагают следующие условия: первые два месяца- 11%, в третий месяц – 12% и последние три месяца- 13%. В каком банке более выгодные условия кредита? Чему равна разница в сумме процентов по кредиту? Задача 4. Сравните величину процентов, начисленных при выдаче кредита размеров 500 тыс. руб., выданного на срок с 5 июня по 18 сентября текущего года по ставке 18% годовых. Используйте при расчетах три схемы начисления процентов. Задача 5. При открытии депозита при ставке 8% годовых 20 апреля на счет была положена сумма 100 тыс. руб. Затем 5 ноября того же года на счет было добавлено 200 тыс. руб. 10 сентября со счета сняли 75 тыс. руб., а 20 ноября счет был закрыт. Какую сумму получил вкладчик при закрытии счета? Задача 6. Через 120 дней с момента подписания кредитного договора заемщик должен вернуть банку 750 тыс. руб. Процентная ставка по кредиту равна 18% годовых. Чему равна первоначальная сумма долга? Самостоятельная работа. Простые учетные ставки. Цель работы - научиться проводить расчеты по схеме простых учетных процентов, используя формулы финансовых вычислений. О  сновные формулы сновные формулы 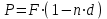 (2.1) (2.1) 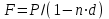 (2.2) (2.2) 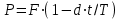 (2.3) (2.3)  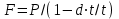 (2.4) (2.4)D=F-P=Fnd(2.5) 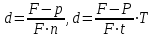 (2.6) (2.6) 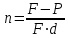 (2.7.) (2.7.) 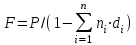 (2.8) (2.8)где P- вложенная сумма (сумма, которую получает владелец векселя при его учете); F– наращенная сумма (номинальная стоимость векселя); n- количество периодов продолжительности финансовой операции; d-простаяучетная ставка; t -продолжительность финансовой операции в днях; количество дней в году; D- дисконт. Контрольные вопросы В каких случаях применяется операция банковского дисконтирования? Верно ли, что по простой учетной ставке вексель можно учесть за любое время до срока погашения? В чем различие между антисипативным и декурсивным способом начисления процентов? Типовые задачи с решениями Задача 1. В банк 6 мая предъявлен для учета вексель, на сумму 140 тыс. руб. со сроком погашения 10 июля того же года. Банк учитывает вексель по учетной ставке 40% годовых, считая, что в году 365 дней. Определить сумму, получаемую векселедержателем от банка, и комиссионные, удерживаемые банком за свою услугу. За какое время до срока платежа операция учета векселя имеет смысл? Решение По формуле (2.1) при F = 140.; n = 65/365, d = 0,4 получим: Р = 140(1-0,4 65/365)=129, 89 Векселедержатель получит от банка 129,89 тыс. руб. Комиссионные банка ( или дисконт) определяются по формуле D= F - P D= F - P= 140-129, 89=10, 11 тыс. руб. Комиссионные, удерживаемые банком за свою услугу, равны 10,11 тыс. руб. Учет векселя по учетной ставке имеет смысл при n<1/d, для этой задачи при n< 2,5 года. При n>2,5 года сумма Р, которую должен получить владелец векселя при его учете, становится отрицательной. Задача 2. Кредит в размере 400 тыс. руб. выдан по простой учетной ставке 25% годовых. Определить срок кредита, если заемщик планирует получить на руки 350 тыс. руб. Решение По формуле (2.7. ) при F =400 ; Р=350; d=0,25 получаем: n = (400-350)/(4000,25)=0,5 Срок кредита равен 0,5 года. Задачи для самостоятельной работы. Задача 1. 10 апреля предприниматель получил ссуду в банке под простую учетную ставку 20 % годовых и должен возвратить 18 ноября того же года 750 тыс. руб. Определить точным и приближенным способами сумму, полученную клиентом. Задача 2. Предприниматель получил ссуду в 600 тыс. руб. на полгода. Банк предоставляет ссуду на условиях начисления простых учетных процентов по ставке 16% годовых. Какую сумму предприниматель будет должен банку? Задача 3. Векселедержатель 1 октября предъявил для учета вексель на сумму 600 тыс. руб. со сроком погашения 25 октября текущего года. Банк учел вексель по простой учетной ставке 20% годовых . Какую сумму получит векселедержатель от банка? Самостоятельная работа. Сложные ссудные ставки. Цель работы - научиться проводить расчеты по схеме сложных ссудных процентов, используя формулы финансовых вычислений; провести сравнение финансовых операций при использовании простых и сложных ставок.  Основные формулы F=P∙ (1 + r) 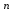 (3.1) (3.1)P = F /(1 + r)n (3.2) F = P (1 + r/m)nm(3.3) F = P (1 + r)w+f (3.4) F=P(1+r)w.(1+f∙r) (3.5) 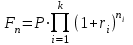 (3.6) (3.6)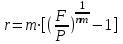 (3.7) (3.7)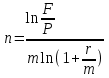 (3.8) (3.8)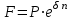 (3.9) (3.9)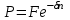 (3.10) (3.10)где F– наращенная сумма; P- вложенная сумма; n- количество лет; r- сложнаяпроцентная ставка; m- количество начислений процентов в году; w- целая часть периода финансовой операции; f- дробная часть периода финансовой операции. Контрольные вопросы Чему равен множитель наращения при начислении процентов по сложной ссудной ставке? Как соотносятся между собой наращенные суммы при начислении простых и сложных ссудных процентов? Верно ли, что начисление сложных процентов по ставке 12% годовых эквивалентно начислению сложных процентов по ставке 1% в месяц? Как пользоваться финансовыми таблицами при вычислении наращенной и приведенной стоимости? Типовые задачи с решениями Задача 1. На вашем счёте в банке 15 млн. руб. Банковская ставка по депозитам равна 12% годовых. Вам предлагают войти всем капиталом в организацию совместного предприятия, обещая удвоение капитала через 5 лет. Принимать ли это предложение? Решение. Для решения задачи используем формулу (3.1.). Если мы вложим деньги в банк, то через 5 лет получим следующую сумму: F = 15∙(1 + 0,12)5 = 26,43 млн.руб. Если мы войдем всем капиталом в организацию совместного предприятия, то наш капитал удвоится: F = 15 2 = 30 млн. руб. Следует принять данное предложение и не вкладывать деньги в банк. Задача 2. За выполненную работу предприниматель должен получить 600 тыс. руб. Заказчик не имеет возможности рассчитаться в данный момент и предлагает отложить срок уплаты на 2 года, по истечении которых он обязуется выплатить 730 тыс. руб. Выгодно ли это предпринимателю, если приемлемая норма прибыли составляет 10%? Какова минимальная ставка, которая делает подобные условия невыгодными для предпринимателя? Решение. Для решения задачи используем формулу (3.1). Будущая стоимость 600 тыс.руб. через 2 года при норме прибыли 10% составит: F = 600 тыс.руб. (1 + 0,1)2 = 720,6 тыс.руб. Это меньше, чем 730 тыс. руб., поэтому предпринимателю выгодно ждать расчета 2 года. Для расчета минимальной ставки, которая делает условия невыгодными, воспользуемся формулой (2.6) при m=1: r = (730 /600)1/2 – 1 = 0,1030 =10,3 % Минимальная ставка, которая делает условия невыгодными для предпринимателя, равна 10,3 % годовых. Задачи для самостоятельной работы. Задача 1. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25 % процента годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально. Задача 2. В банк вложены деньги в сумме 800 тыс. руб. на полтора года под 10% годовых с ежеквартальным начислением сложных процентов. Определите доход клиента в этой финансовой операции. Задача 3. Банк предоставил ссуду в размере 500 тыс. руб. на 33 месяца под процентную ставку 28% годовых на условиях ежегодного начисления процентов. Какую сумму нужно будет вернуть банку по окончании срока при использовании следующих условиях: 1) при расчетах используется схема сложных процентов; б) при расчетах используется смешанная схема? Самостоятельная работа. Сложные учетные ставки. Цель работы - научиться проводить расчеты по схеме сложных ссудных процентов, используя формулы финансовых вычислений; провести сравнение финансовых операций при использовании простых и сложных ставок.  Основные формулы 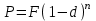 (4.1) (4.1)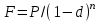 (4.2) (4.2)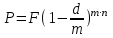 (4.3) (4.3)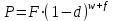 (4.4) (4.4)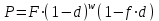 (4.5) (4.5)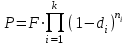 (4.6) (4.6)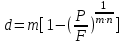 (4.7) (4.7) 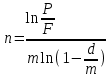 (4.8) (4.8)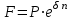 (4.9) (4.9)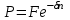 (4.10) (4.10)где F– наращенная сумма; P- вложенная сумма; n- количество лет; d- сложная учетная ставка;  непрерывная ставка непрерывная ставка m- количество начислений процентов в году; w- целая часть периода финансовой операции; f- дробная часть периода финансовой операции. Контрольные вопросы Чему равен множитель дисконтирования при дисконтировании по сложной учетной ставке? Может ли учет по сложной учетной ставке привести к отрицательным значениям? Что происходит с величиной учтенного капитала, если растет число осуществлений операций дисконтирования по сложной учетной ставке? Типовые задачи с решениями Задача 1. Вексель на сумму 70 тыс. руб. со сроком погашения через 4 года учтен за 32 месяца по сложной учетной ставке 24% годовых. Определить суммы, которые получит предъявитель векселя при различных способах учета. Решение 1) При применении схемы сложных процентов воспользуемся формулой (4.4) при n = 32/12= 8/3, F = 70 тыс. руб., d = 0,24, поэтому  Владелец векселя получит 33 672 руб. 2) При применении смешанной схемы воспользуемся формулой (4.4) при w = 2, f = 2/3:  Владелец векселя получит 33 672 руб. Задача 2. Вексель был учтен за 2,5 года до срока его погашения, при этом владелец векселя получил четверть от написанной на векселе суммы. По какой годовой учетной ставке был учтен этот вексель, если производилось 1) поквартальное дисконтирование; 2) ежемесячное дисконтирование. Решение 1) по формуле (4.7) при P=0,25F; n=2,5; m=4, получим :  Вексель был учтен по сложной учетной ставке 51,78% годовых. 2) по формуле (4.7) при P=0,25F; n=2,5; m=12, получим : 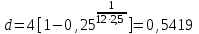 Вексель был учтен по сложной учетной ставке 54,19 % годовых. Задачи для самостоятельной работы. Задача 1. Вексель на сумму 800 тыс. руб. учитывается за 2 года до срока погашения. Какую сумму получит предъявитель векселя при учете по сложной учетной ставке 20% годовых? Задача 2. Определите дисконтированную сумму при учете 100 тыс. руб. по простой и сложной учетной ставкам, если годовая ставка равна 18% годовых и учет происходит за 30 дней, 180 дней, 1 год, 3 года, 5 лет. Полагать год равным 360 дней. |
