Сборник самостоятельных работ. московский колледж бизнестехнологий
 Скачать 281.08 Kb. Скачать 281.08 Kb.
|
Самостоятельная работа. Финансовые ренты.Ц  ель работы - научиться решать прямую и обратную задачи оценки аннуитета, используя формулы финансовых вычислений. ель работы - научиться решать прямую и обратную задачи оценки аннуитета, используя формулы финансовых вычислений. Основные формулы 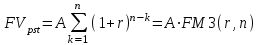 (9.1) (9.1)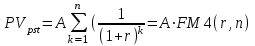 (9.2) (9.2)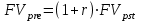 (9.3) (9.3)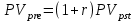 (9.4) (9.4)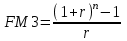 (9.5) (9.5)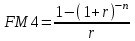 (9.6) (9.6)Контрольные вопросы Какой денежный поток называется потоком пренумерандо? Приведите пример. Какой денежный поток называется потоком постнумерандо? Приведите пример. Как используются финансовые таблицы для оценки постоянных аннуитетов? Чему равен коэффициент наращения аннуитета? Чему равен коэффициент дисконтирования аннуитета? Какая связь существует между будущей и приведенной стоимостями аннуитета? Типовые задачи с решениями Задача 1. Какую сумму необходимо поместить в банк под сложную процентную ставку 6% годовых, чтобы в течение 6 лет иметь возможность в конце каждого года снимать со счета 100 тыс. руб., исчерпав счет полностью, если банком ежегодно начисляются сложные проценты? Решение Для ответа на поставленный вопрос необходимо определить приведенную стоимость аннуитета постнумерандо. По формуле (9.2) при А =100; r=6%; n=6: PV=100FM4(6%,6)=1004,917=491,7 В банк на счет необходимо положить 491 700 руб. Задача 2. Клиент в конце каждого года вкладывает 300 тыс. руб. в банк, ежегодно начисляющий сложные проценты по ставке 10% годовых. Определить сумму, которая будет на счете через 7 лет. Если эта сумма получается в результате однократного помещения денег в банк, то какой величины должен быть взнос? Решение По формуле (9.1) при A=300; r=10%; n=7: FV=300FM3(10%,7)=3009,487=2846,1. Через 7 лет на счете накопится 2846100 руб. Величину однократного взноса в начале первого года находим по формуле (3.2, Занятие Сложные ссудные ставки) при F=2846,1; r=10%; n=7: P=2846,1FM2(10%,7)=2846,1∙0.51 =1450,44 Взнос равен 1450440 руб. Задачи для самостоятельной работы. Задача 1. Предприниматель планирует после выхода на пенсию обеспечить себе ежегодный годовой доход в размере 60 тыс. руб. в течение 8 лет. Какую сумму ему необходимо для этого поместить на депозит в момент выхода на пенсию, если банковская ставка по депозитам будет 10% годовых? Предприниматель планирует снимать денежные средства с депозита в начале каждого года и за 8 лет исчерпать депозит полностью. Задача 2. В начале каждого года в течение 13 лет на счет вносится 130 тыс. рублей, процентная ставка составляет 13% годовых. Определить наращенную сумму через 13 лет. Задача 3. Сумма 75 тыс. рублей вносится в конце каждого года на протяжении 18 лет под 13% годовых. Определить величину накопленного вклада через 18 лет. Задача 4. Найти дисконтированную величину 16 вкладов постнумерандо по 100 тыс. рублей при ставке 14% годовых на текущий момент времени и через 3 года. Задача 5. Найти текущую стоимость суммы 15 вкладов пренумерандо по 75 тыс. рублей при ставке 20% годовых. Задача 6. Какую сумму необходимо поместить в банк под сложную процентную ставку 10% годовых, чтобы в течение 12 лет иметь возможность в конце каждого года снимать со счета 120 тыс. руб., исчерпав счет полностью, если банком ежегодно начисляются сложные проценты? Самостоятельная работа. Практическое приложение финансовых вычислений.Рассмотрим практическое приложение финансовых вычислений на примере планирования погашения задолженности и ипотечных кредитов.  Цель работы – рассмотреть способы практических приложений финансовых вычислений, научиться выбирать оптимальную схему погашения задолженности и ипотечных кредитов, используя формулы финансовых вычислений и электронные таблицы EXCEL. Контрольные вопросы Какой кредит называется потребительским? Приведите примеры потребительских кредитов Перечислите основные способы погашения кредита Какой способ погашения кредита наиболее выгоден банку (кредитору)? Какой способ погашения кредита наиболее выгоден заемщику? Почему банки заинтересованы в том, чтобы должник погашал сумму долга частями в течение всего срока кредитования? Типовые задачи с решениями Пусть заем в сумме Р выдан под r простых ссудных процентов на n периодов. К концу финансовой операции величина займа составит величину 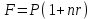 . .Если предполагается возвращать займ одним платежом в конце срока финансовой операции, то величина F и есть размер возвращаемого платежа. Задача 1. Погашение основного долга одним платежом. Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить общую сумму выплат, если ссуда возвращается способом «погашение основного долга одним платежом в конце срока финансовой операции». Решение Величина процентных платежей за 8 лет составит rPn=0,155=2,5 Общая сумма выплат составит 2,5 млн.+ 5 млн. =7,5 млн.руб. Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. При погашении основного долга равными годовыми выплатами в конце каждого года выплачивается n-ная доля основного долга и проценты, начисленные на сумму долга, которой пользовались в течение года. В конце первого года выплачивается доля основного долга, равная величине P/n и выплачиваются проценты с суммы Р, которой пользовались в течение года, равные величине rP. Общий платеж в конце первого года равен величине P/n+ rP. В конце второго года выплачивается доля основного долга, равная величине P/n и выплачиваются проценты с суммы (Р- P/n), которой пользовались в течение года, равные величине r (Р- P/n). Общий платеж в конце второго года равен величине P/n+ r (Р- P/n). В общем случае в конце года k+1 общий платеж равен величине P/n+ r (Р- kP/n). Платежи каждого года образуют арифметическую прогрессию с разностью d=rP/n, первым членом a1 =P/n+ rPи последним членом an=P/n+ rP/n. Сумма n членов арифметической прогрессии равна 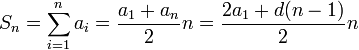 Величина выплат составит 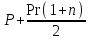 Задача 2. Погашение займа равными годовыми выплатами Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить общую сумму выплат, если ссуда возвращается способом «погашение займа равными годовыми выплатами». Решение Величину ежегодного платежа находим из уравнения 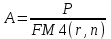 при Р=5; r = 0,1; n =5; FM4(10%,5)=3,791 при Р=5; r = 0,1; n =5; FM4(10%,5)=3,791A=1318,913 Общая сумма выплат составит 51318,913= 6 594 566 руб. Взятый заем может погашаться различными способами. Например, заемщик может создать специальный погасительный фонд и накапливать в нем средства, чтобы погасить заем одним платежом в конце срока финансовой операции. Очевидно, что это возможно только в том случае, если у заемщика есть возможность накапливать деньги в некотором фонде под более высокий процент. Пусть заем в сумме Р выдан под r1 сложных ссудных процентов на n периодов. Тогда к конце срока финансовой операции финансовой операции величина займа составит величину 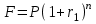 . Платежи в погасительный фонд составляют годовую ренту с ежегодным платежом, равным А и процентной ставкой r2 > r1, будущая стоимость этой ренты равна величине . Платежи в погасительный фонд составляют годовую ренту с ежегодным платежом, равным А и процентной ставкой r2 > r1, будущая стоимость этой ренты равна величине 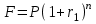 . . Тогда величину ежегодного платежа в погасительный фонд находим из уравнения: 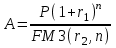 Задачи для самостоятельной работы. Задача 1. Кредит в размере К = 400 тыс. руб., выданный на год под простую ссудную ставку 20% годовых, должен погашаться четырьмя платежами в конце каждого квартала. Долг погашается равными выплатами, т.е. в каждый квартал погашается 100 тыс. руб. основного долга. Определить величину каждой квартальной выплаты, состоящей из погашаемой ¼ части основного долга и процентов с суммы задолженности за соответствующий квартал. Задача 2. Кредит в сумме 100 млн.руб. выдан на 5 лет под 20% годовых. Для погашения кредита создается погасительный фонд, на который начисляются проценты по ставке 22% годовых. Фонд формируется в течение 5 лет, взносы производятся в конце каждого года равными суммами. Необходимо найти размер срочных выплат. |
