|
|
Лабораторная работа № 32, Вариант 17, гр. БИК 2006, Саакян. московскокий технический университет связи и информатики
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«МОСКОВСКОКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»
(МТУСИ)
Факультет Радио и Телевидение
Кафедра теории электрических цепей
Лабораторная работа № 32
“Исследование пассивных цепей при гармоническом
воздействии на постоянной частоте”
по дисциплине
Теоретические основы электротехники
Выполнил: студент группы БИК2006 Саакян Э. А.
Проверил: к.т.н. Мосичев А. В.
Москва 2021 г.
Цель работы:
С помощью программы Micro-Cap исследовать электрический режим конденсатора и катушки индуктивности в цепях гармонического тока. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
Исходные данные
Вариант 17
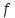 =1,2,3,4,5 кГц – частота; =1,2,3,4,5 кГц – частота;
R = 3,017 кОм – сопротивление резистора (3000+номер варианта);
E=U=0.9 В – ЭДС источника;
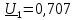 В – входное комплексное напряжение; В – входное комплексное напряжение;
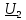 – выходное комплексное напряжение; – выходное комплексное напряжение;
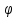 – сдвиг фазы; – сдвиг фазы;
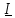 – комплексный ток; – комплексный ток;
j = 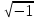 – мнимая единица; – мнимая единица;
Для конденсатора
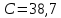 нФ – емкость конденсатора; нФ – емкость конденсатора;
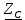 – комплексное сопротивление конденсатора; – комплексное сопротивление конденсатора;
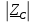 – модуль комплексного сопротивления конденсатора; – модуль комплексного сопротивления конденсатора;
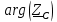 – фаза комплексного сопротивления конденсатора; – фаза комплексного сопротивления конденсатора;
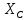 – ёмкостное сопротивление конденсатора; – ёмкостное сопротивление конденсатора;
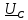 – комплексное напряжение на конденсаторе; – комплексное напряжение на конденсаторе;
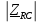 – модуль комплексного сопротивления RC-цепи; – модуль комплексного сопротивления RC-цепи;
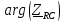 – фаза комплексного сопротивления RC-цепи; – фаза комплексного сопротивления RC-цепи;
Для катушки индуктивности
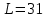 мГн – индуктивность катушки; мГн – индуктивность катушки;
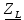 – комплексное сопротивление катушки; – комплексное сопротивление катушки;
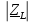 – модуль комплексного сопротивления катушки; – модуль комплексного сопротивления катушки;
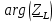 – фаза комплексного сопротивления катушки; – фаза комплексного сопротивления катушки;
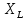 – индуктивное сопротивление катушки; – индуктивное сопротивление катушки;
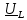 – комплексное напряжение на катушке; – комплексное напряжение на катушке;
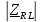 – модуль комплексного сопротивления RL-цепи; – модуль комплексного сопротивления RL-цепи;
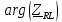 – фаза комплексного сопротивления RL-цепи; – фаза комплексного сопротивления RL-цепи;
Расчетные формулы:
Для C-цепи:
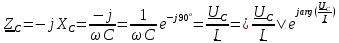 - комплексное сопротивление конденсатора; - комплексное сопротивление конденсатора;
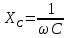 – ёмкостное сопротивление конденсатора; – ёмкостное сопротивление конденсатора;
Для L-цепи:
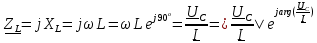 – комплексное сопротивление катушки; – комплексное сопротивление катушки;
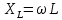 – индуктивное сопротивление катушки; – индуктивное сопротивление катушки;
Закон ома для комплексных величин:
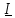 = =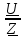 – комплексный ток; – комплексный ток;
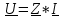 – комплексное падение напряжения; – комплексное падение напряжения;
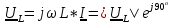 – комплексное напряжение на катушке; – комплексное напряжение на катушке;
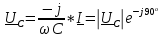 – комплексное напряжение на конденсаторе. – комплексное напряжение на конденсаторе.
Ход работы:
C-цепь
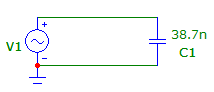
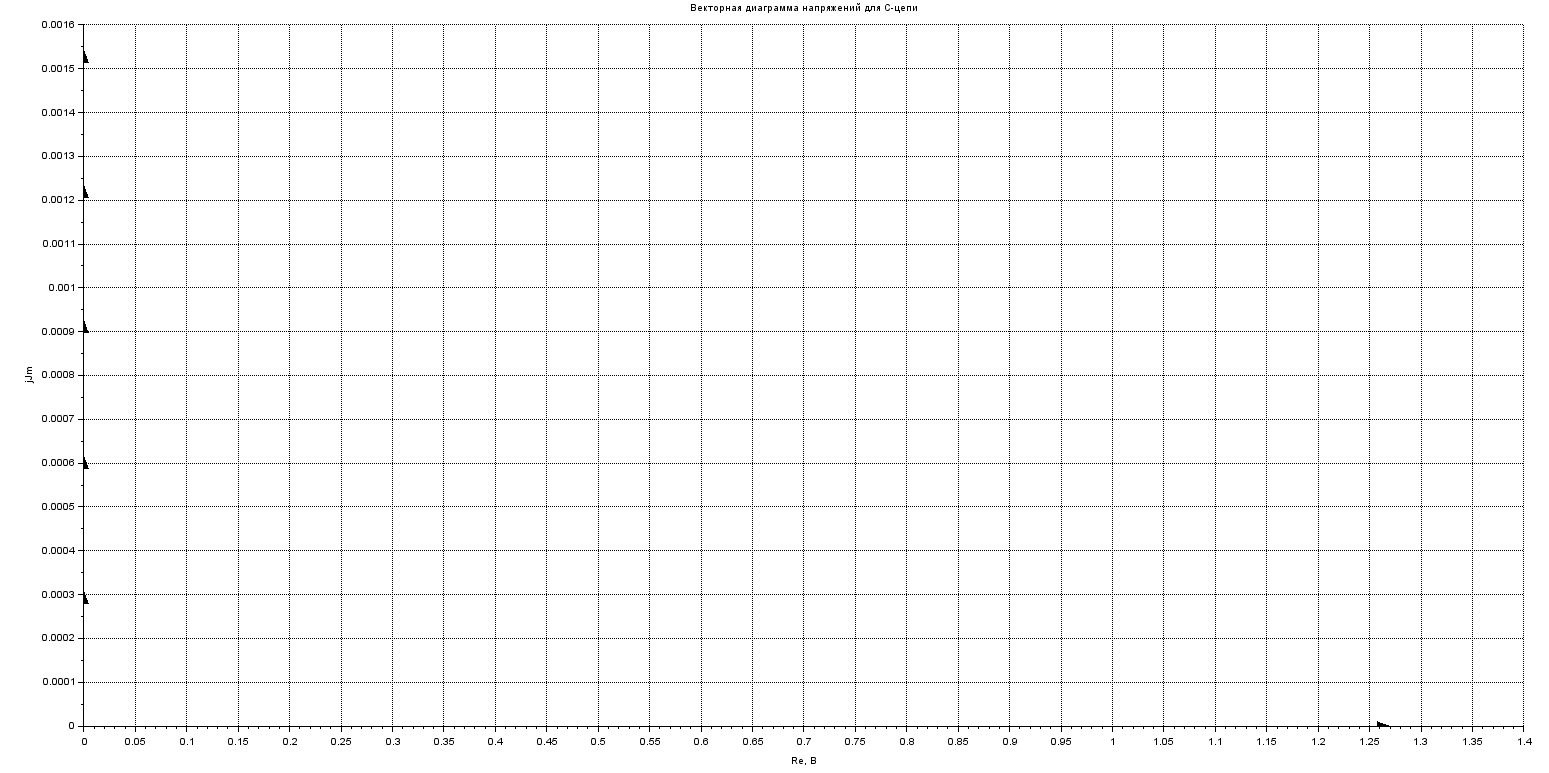
Диаграмма напряжений RL-цепи
По предварительному расчёту
|
Получено экспериментально
|
f, кГц
|
C, нФ
|
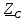 , Ом , Ом
|
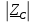 ,Ом ,Ом
|
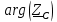 град град
|
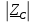 ,Ом ,Ом
|
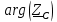 , град , град
|
1
|
38,7
|
-4112.5308i
|
4112.5308
|
-89.99
|
4113
|
-90
|
2
|
38,7
|
-2056.2654i
|
2056.2654
|
-90
|
2056
|
-90
|
3
|
38,7
|
-1370.8436i
|
1370.8436
|
-90
|
1371
|
-90
|
4
|
38,7
|
-1028.1327i
|
1028.1327
|
-90
|
1028
|
-90
|
5
|
38,7
|
-822.50617i
|
822.50617
|
-90
|
822.506
|
-90
|
--> f=[1000:1000:5000]; //Задаем частоту, Гц
--> U=1.27; //Входное напряжение, В
--> C=38.7*10^-9; // Задаем емкость конденсатора, Гн
--> Xc=1./(2.*%pi.*f.*C) //Высчитываем реактивное сопротивление конденсатора, Ом
Xc =
4112.5308 2056.2654 1370.8436 1028.1327 822.50617
--> Omega=2*%pi.*f //Высчитываем угловую скорость, радиан/с
Omega =
6283.1853 12566.371 18849.556 25132.741 31415.927
--> Zc=-(%i)./(2.*%pi.*f.*C)//Высчитываем комплексное сопротивление конденсатора, Ом
Zc =
0. - 4112.5308i 0. - 2056.2654i 0. - 1370.8436i 0. - 1028.1327i 0. - 822.50617i
--> Ic=U./Xc//Высчитываем силу тока на конденсаторе, А
Ic =
0.0003088 0.0006176 0.0009264 0.0012352 0.0015441
--> ArgZc=-(180/%pi).*atan(2*%pi*f.*1./(Xc.*C)) //Высчитываем фазу комплексного сопротивления конденсатора, град
ArgZc =
-89.999999 -90. -90. -90. -90.
--> N=length(f);
--> for i=1:N
> x=[0 0];
> y=[0 Ic(i)];
> plot2d4(x,y) //Векторы UC
> x=[0 U];
> y=[0 0];
> plot2d4(x,y) //Вектор U
> end
--> xtitle ("Векторная диаграмма напряжений для C-цепи","Re, В","jJm, A") //Подписи графика и осей
--> xgrid // Координатная сетка
|
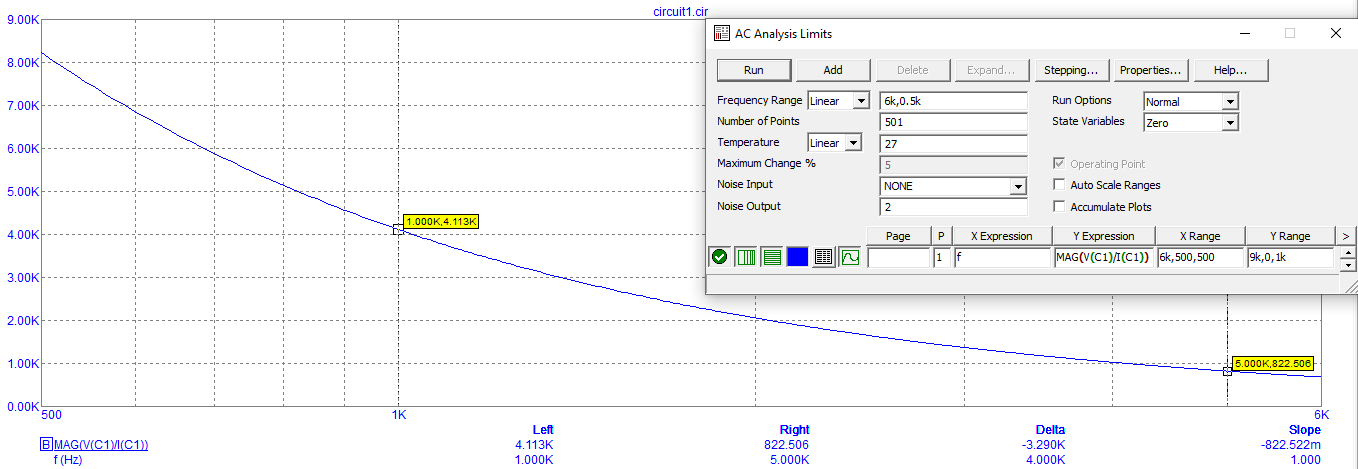
График зависимости модуля сопротивления в C-цепи от частоты
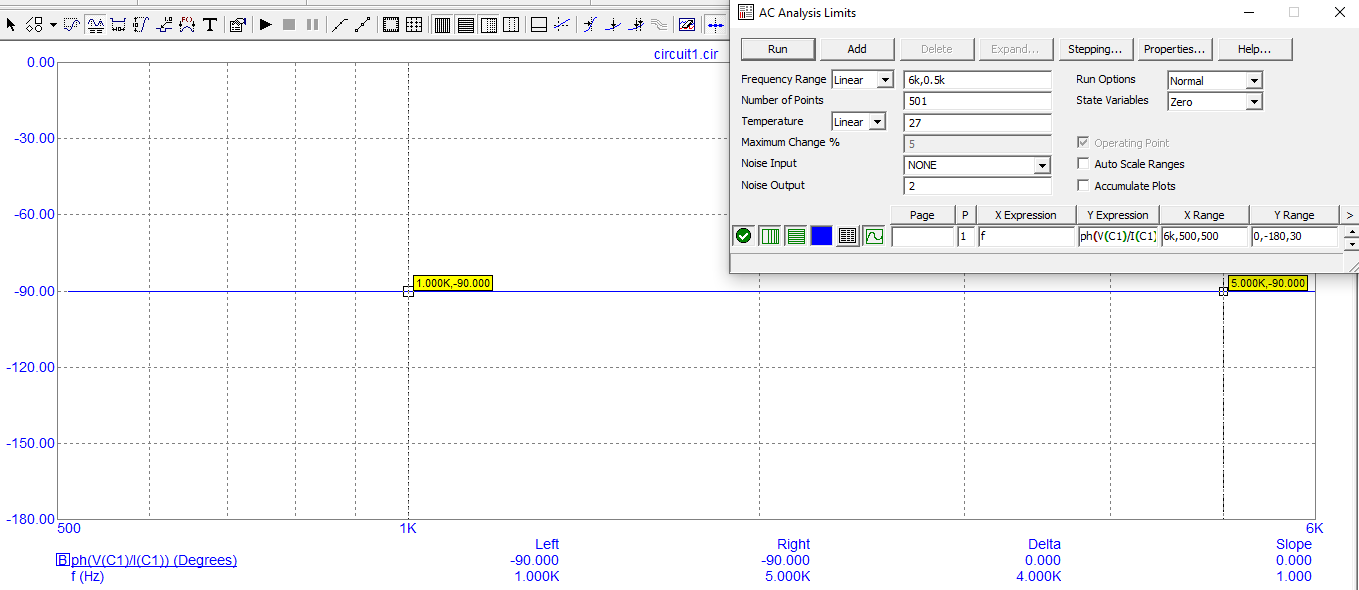
График зависимости фазы сопротивления С-цепи от частоты
RC-цепь
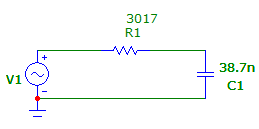
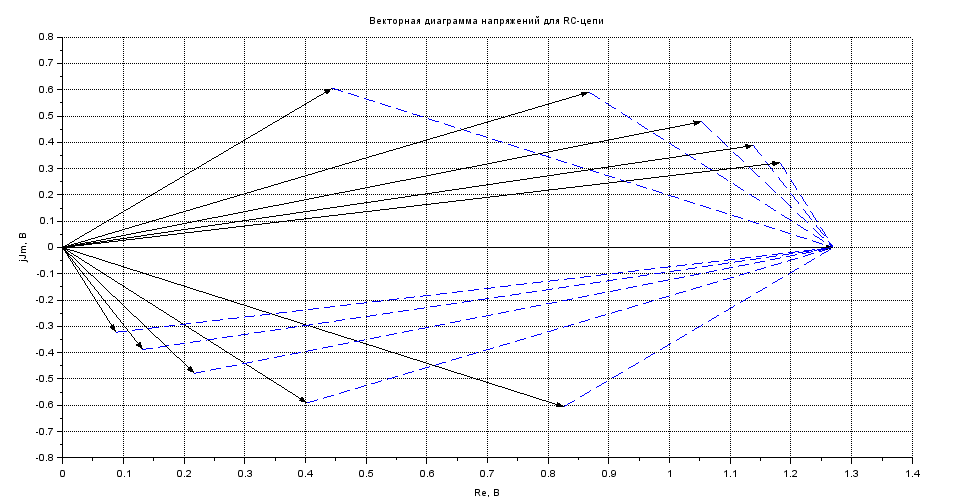
Диаграмма напряжений RC-цепи
По предварительному расчёту
|
Получено экспериментально
|
f,кГц
|
С,нФ
|
R,
кОм
|
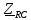 ,Ом ,Ом
|
|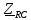 |,Ом |,Ом
|
arg|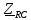 |, град |, град
|
|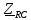 |, Ом |, Ом
|
arg|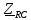 |, град |, град
|
1
|
38,7
|
3,017
|
3017. - 4112.5308i
|
5100.5097
|
- 53.735799
|
5101
|
-53.736
|
2
|
38,7
|
3,017
|
3017. - 2056.2654i
|
3651.098
|
-34.276763
|
3651
|
-34.277
|
3
|
38,7
|
3,017
|
3017. - 1370.8436i
|
3313.8348
|
-24.435769
|
3314
|
-24.436
|
4
|
38,7
|
3,017
|
3017. - 1028.1327i
|
3187.3729
|
-18.818074
|
3187
|
-18.818
|
5
|
38,7
|
3,017
|
3017. - 822.50617i
|
3127.1082
|
-15.249603
|
3127
|
-15.25
|
По предварительному расчёту
|
Получено экспериментально
|
f, кГц
|
С, нФ
|
R, кОм
|
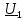 ,В ,В
|
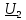 ,В ,В
|
arg|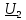 |,град |,град
|
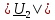 ,В ,В
|
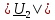 ,В ,В
|
arg|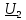 |,град |,град
|
1
|
38,7
|
3,017
|
0,707
|
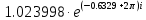
|
-36.345633
|
1.0239985e+0
|
0.806293
|
-36.264
|
2
|
38,7
|
3,017
|
0,707
|
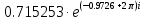
|
-55.802617
|
7.152525e-1
|
0.563190
|
-55.723
|
3
|
38,7
|
3,017
|
0,707
|
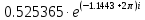
|
-65.628443
|
5.253646e-1
|
0.413672
|
-65.564
|
4
|
38,7
|
3,017
|
0,707
|
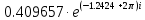
|
-71.233972
|
4.096567e-1
|
0.322563
|
-71.182
|
5
|
38,7
|
3,017
|
0,707
|
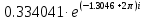
|
-74.793649
|
3.340412e-1
|
0.263024
|
-74.750
|
--> f=[1000:1000:5000]; //Задаем значение частоты, Гц
--> R=3017; //Задаем значение резистора R1, Ом
--> C=38.7*10^-9; // Задаем емкость конденсатора, Гн
--> ZC=-(%i)./(2.*%pi.*f.*C)//Высчитываем комплексное сопротивление конденсатора, Ом
ZC =
0. - 4112.5308i 0. - 2056.2654i 0. - 1370.8436i 0. - 1028.1327i 0. - 822.50617i
--> U1=1.27; // Задаем входное напряжение, В
--> Zrc=R+(1./( %i.* 2.*%pi.*f.*C)) // Считаем комплексное сопротивление RC-цепи, Ом
Zrc =
3017. - 4112.5308i 3017. - 2056.2654i 3017. - 1370.8436i 3017. - 1028.1327i 3017. - 822.50617i
--> MZrc=abs(Zrc); // Высчитываем модуль сопротивления RC-цепи, Ом
--> Il=U1./Zrc; // Высчитываем комплексный ток, А
--> U2=Il.*ZC // Высчитываем комплексное сопротивление на конденсаторе, В
U2 =
column 1 to 4
0.8256479 - 0.6057048i 0.4028238 - 0.5910323i 0.2173291 - 0.4783053i 0.1321406 - 0.3877595i
column 5
0.087861 - 0.3222793i
--> MU2=abs(U2) // Находим модуль комплексного сопротивления на конденсаторе, В
MU2 =
1.0239985 0.7152525 0.5253646 0.4096567 0.3340412
--> UR=Il.*R; // Находим комплексное напряжение на резисторе R1, В
--> URmod=abs(UR); //Находим модуль напряжения на резисторе, В
--> arg_UR=-atan(imag(UR),real(UR))*180/%pi //Находим фазу напряжения на резисторе, град
arg_UR =
-53.735799 -34.276763 -24.435769 -18.818074 -15.249603
--> UR_Re=real(UR); // Действительная часть напряжения на резисторе
--> UR_Jm=imag(UR); // Мнимая часть напряжения на резисторе
--> arg_UC=atan(imag(U2),real(U2))*180/%pi // Находим фазу напряжения на конденсаторе, град
arg_UC =
-36.264201 -55.723237 -65.564231 -71.181926 -74.750397
--> UC_Re=real(U2); // Действительная часть напряжения на конденсаторе
--> UC_Jm=imag(U2); // Мнимая часть напряжения на конденсаторе
--> b1=UR_Jm./UR_Re;
--> a1=UC_Jm-b1.*UC_Re;
--> b2=UC_Jm./UC_Re;
--> a2=UR_Jm-b2.*UR_Re;
--> N=length(f);
--> //Построение векторной диаграммы
--> for i=1:N
> x=[0 UR_Re(i)];
> y=[0 UR_Jm(i)];
> plot2d4(x,y) //Векторы UR
> x=[0 UC_Re(i)];
> y=[0 UC_Jm(i)];
> plot2d4(x,y) //Векторы UC
> x=[0 (UC_Re(i)+UR_Re(i))];
> y=[0 (UC_Jm(i)+UR_Jm(i))];
> plot2d4(x,y) //Вектор U
> x1=UC_Re(i):0.1*UR_Re(i):(UC_Re(i)+UR_Re(i));
> y1=a1(i)+b1(i).*x1;
> plot(x1,y1,'b--')
> x2=UR_Re(i):0.1*UC_Re(i):(UC_Re(i)+UR_Re(i));
> y2=a2(i)+b2(i).*x2;
> plot(x2,y2,'b--')
> end
--> xtitle ("Векторная диаграмма напряжений для RC-цепи","Re, В","jJm, В") //Подписи графика и осей
--> //Координатная сетка
--> xgrid
--> //Почастотный вывод напряжений и их фаз
--> for i=1:N
> mprintf('f=%4.0f URmod=%5.4f arg_UR=%5.2f MU2=%5.4f arg_UC=%5.2f\n',f(i),URmod(i),arg_UR(i),MU2(i),arg_UC(i))
> end
f=1000 URmod=0.7512 arg_UR=-53.74 MU2=1.0240 arg_UC=-36.26
f=2000 URmod=1.0494 arg_UR=-34.28 MU2=0.7153 arg_UC=-55.72
f=3000 URmod=1.1562 arg_UR=-24.44 MU2=0.5254 arg_UC=-65.56
f=4000 URmod=1.2021 arg_UR=-18.82 MU2=0.4097 arg_UC=-71.18
f=5000 URmod=1.2253 arg_UR=-15.25 MU2=0.3340 arg_UC=-74.75
|
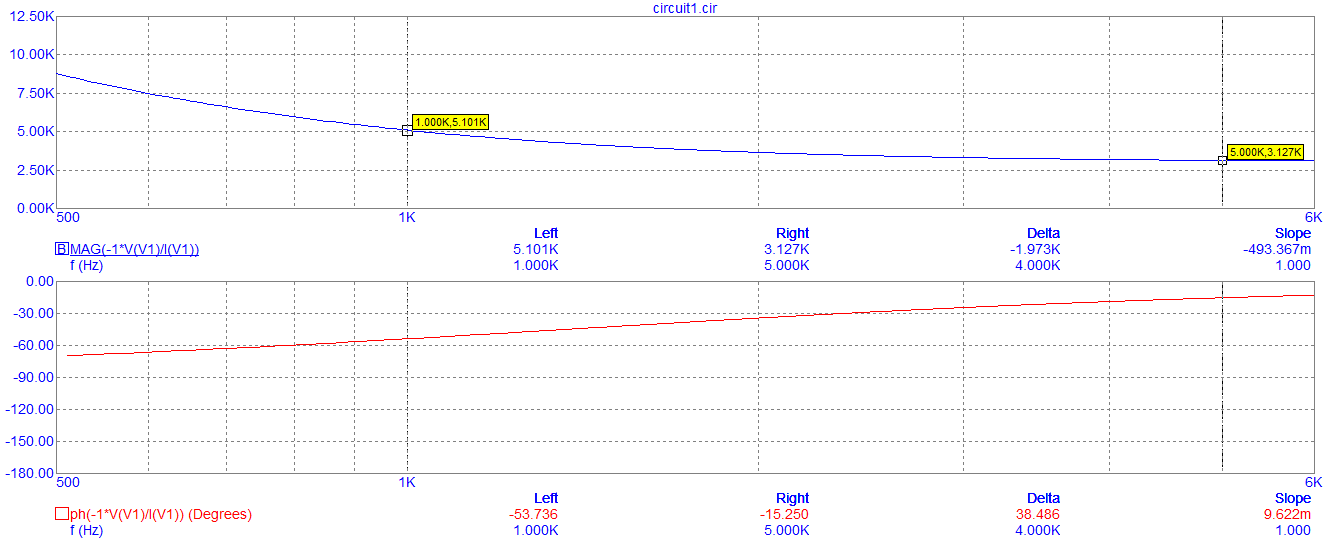
Графики зависимости модуля и фазы комплексного сопротивления RC-цепи от частоты
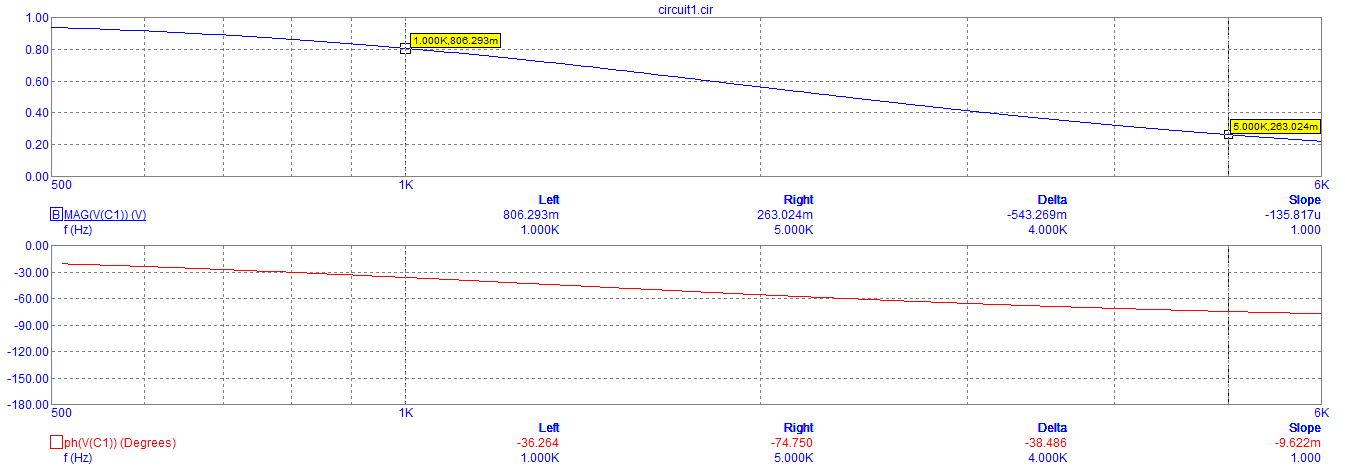
Графики зависимости модуля и фазы комплексного напряжения конденсатора RC-цепи от частоты
L-цепь

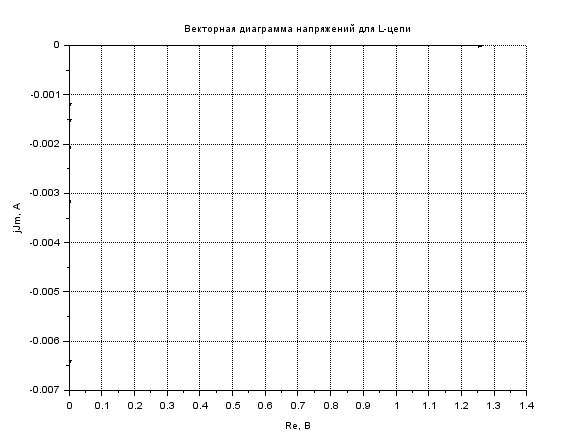
Диаграмма напряжений L-цепи
По предварительному расчёту
|
Получено экспериментально
|
f, кГц
|
L, мГн
|
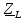 , Ом , Ом
|
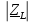 ,Ом ,Ом
|
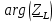 град град
|
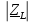 ,Ом ,Ом
|
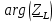 , град , град
|
1
|
31
|
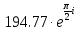
|
1.9477874e+2
|
90
|
1.94779e+2
|
90
|
2
|
31
|
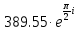
|
3.8955749e+2
|
90
|
3.89557e+2
|
90
|
3
|
31
|
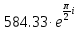
|
5.8433623e+2
|
90
|
5.84336e+2
|
90
|
4
|
31
|
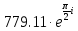
|
7.7911498e+2
|
90
|
7.79115e+2
|
90
|
5
|
31
|
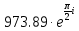
|
9.7389372e+2
|
90
|
9.73894e+2
|
90
|
--> f=[1000:1000:5000]; //Задаем частоту, Гц
--> L=31*10^-3;// Задаем значение индуктивности на катушке L, Гн
--> U=1.27; //Входное напряжение, В
--> Omega=2*%pi.*f //Высчитываем угловую скорость, радиан/с
Omega =
6283.1853 12566.371 18849.556 25132.741 31415.927
--> ZL=%i.*2*%pi*f*L // Высчитываем комплексное сопротивление катушки, Ом
ZL =
0. + 194.77874i 0. + 389.55749i 0. + 584.33623i 0. + 779.11498i 0. + 973.89372i
--> MZL= abs(ZL) // Находим модуль комплексного сопротивления катушки
MZL =
194.77874 389.55749 584.33623 779.11498 973.89372
--> ArgZL = abs((180/%pi).*atan(Omega.*ZL.*L)) // Высчитываем фазу комплексного сопротивления катушки, град
ArgZL =
90. 90. 90. 90. 90.
--> IL=U./MZL//Высчитываем силу тока на катушке, А
IL =
0.0065202 0.0032601 0.0021734 0.0016301 0.001304
--> N=length(f);
--> //Построение векторной диаграммы
--> for i=1:N
> x=[0 0];
> y=[0 -IL(i)];
> plot2d4(x,y) //Векторы UL
> x=[0 U];
> y=[0 0];
> plot2d4(x,y) //Вектор U
> end
--> xtitle ("Векторная диаграмма напряжений для L-цепи","Re, В","jJm, A") //Подписи графика и осей
--> //Координатная сетка
--> xgrid
|
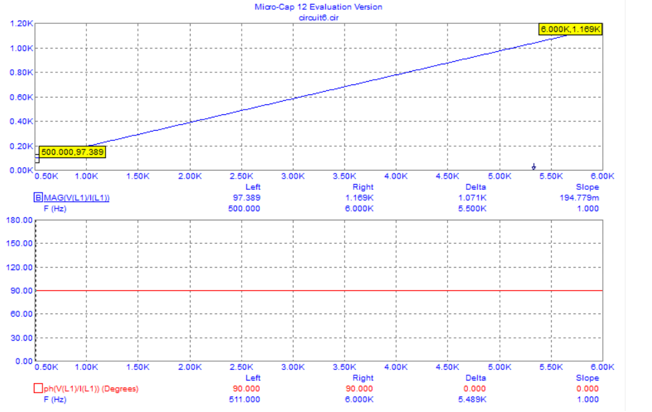
Графики зависимости модуля и фазы комплексного сопротивления катушки L-цепи от частоты.
RL-цепь
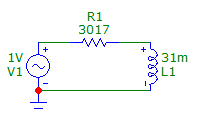
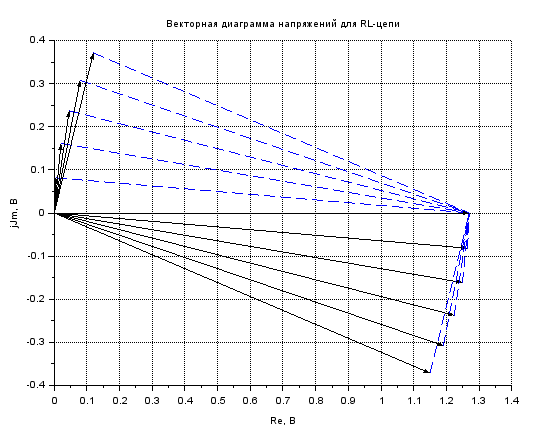
Диаграмма напряжений RL-цепи
По предварительному расчёту
|
Получено экспериментально
|
f,кГц
|
L, мГн
|
R,
кОм
|
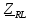 ,Ом ,Ом
|
|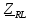 |,Ом |,Ом
|
arg|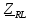 |, град |, град
|
|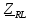 |, Ом |, Ом
|
arg|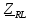 |, град |, град
|
1
|
31
|
3,017
|
3017. + 194.77874i
|
3023.281
|
3.6939123
|
3023
|
3.694
|
2
|
31
|
3,017
|
3017. + 389.55749i
|
3042.046
|
7.35737
|
3042
|
7.357
|
3
|
31
|
3,017
|
3017. + 584.33623i
|
3073.0665
|
10.961398
|
3073
|
10.961
|
4
|
31
|
3,017
|
3017. + 779.11498i
|
3115.9764
|
14.479808
|
3116
|
14.48
|
5
|
31
|
3,017
|
3017. + 973.89372i
|
3170.293
|
17.890185
|
3170
|
17.89
|
По предварительному расчёту
|
Получено экспериментально
|
f, кГц
|
L, мГн
|
R, кОм
|
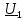 ,В ,В
|
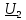 ,В ,В
|
arg|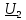 |,град |,град
|
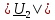 ,В ,В
|
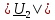 ,В ,В
|
arg|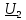 |,град |,град
|
1
|
31
|
3,017
|
0,707
|
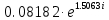
|
86.317044
|
8.18214e-2
|
0.064236
|
86.317
|
2
|
31
|
3,017
|
0,707
|
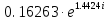
|
82.664274
|
1.626333 e-1
|
0.127683
|
82.664
|
3
|
31
|
3,017
|
0,707
|
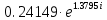
|
79.070417
|
2.414875 e-1
|
0.189602
|
79.07
|
4
|
31
|
3,017
|
0,707
|
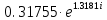
|
75.561456
|
3.175493e-1
|
0.249341
|
75.561
|
5
|
31
|
3,017
|
0,707
|
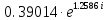
|
72.159647
|
3.901359e-1
|
0.306365
|
72.16
|
--> f=[1000:1000:5000]; //Задаем значение частоты, Гц
--> R=3017; //Задаем значение резистора R1, Ом
--> U1=1.27; // Задаем входное напряжение, В
--> L=31*10^-3;// Задаем значение индуктивности на катушке L, Гн
--> ZL=%i.*2*%pi*f*L; // Высчитываем комплексное сопротивление катушки, Ом
--> Zrl=R+(%i.* (2.*%pi.*f.*L)) // Высчитываем комплексное сопротивление RL-цепи, Ом
Zrl =
3017. + 194.77874i 3017. + 389.55749i 3017. + 584.33623i 3017. + 779.11498i 3017. + 973.89372i
--> MZrl=abs(Zrl) // Высчитываем модуль комплексного сопротивления RL-цепи, Ом
MZrl =
3023.281 3042.046 3073.0665 3115.9764 3170.293
--> Il=U1./Zrl; // Высчитываем комплексный ток, А
--> U2=Il.*ZL // Высчитываем комплексное сопротивление на катушке, В
U2 =
column 1 to 4
0.0052714 + 0.0816514i 0.0208265 + 0.1612943i 0.0459183 + 0.2370816i 0.0793996 + 0.3074626i
column 5
0.1198472 + 0.3712716i
--> MU2=abs(U2) // Находим модуль комплексного сопротивления на катушке, В
MU2 =
0.0818214 0.1626333 0.2414875 0.3175493 0.3901359
--> UR=Il.*R; // Находим комплексное напряжение на резисторе R1, В
--> URmod=abs(UR); //Находим модуль напряжения на резисторе, В
--> arg_UR=-atan(imag(UR),real(UR))*180/%pi //Находим фазу напряжения на резисторе, град
arg_UR =
3.6939123 7.35737 10.961398 14.479808 17.890185
--> UR_Re=real(UR); // Действительная часть напряжения на резисторе
--> UR_Jm=imag(UR); // Мнимая часть напряжения на резисторе
--> arg_UL=atan(imag(U2),real(U2))*180/%pi // Находим фазу напряжения на катушке, град
arg_UL =
86.306088 82.64263 79.038602 75.520192 72.109815
--> UL_Re=real(U2); // Действительная часть напряжения на катушке
--> UL_Jm=imag(U2); // Мнимая часть напряжения на катушке
--> b1=UR_Jm./UR_Re;
--> a1=UL_Jm-b1.*UL_Re;
--> b2=UL_Jm./UL_Re;
--> a2=UR_Jm-b2.*UR_Re;
--> N=length(f);
--> //Построение векторной диаграммы
--> for i=1:N
> x=[0 UR_Re(i)];
> y=[0 UR_Jm(i)];
> plot2d4(x,y) //Векторы UR
> x=[0 UL_Re(i)];
> y=[0 UL_Jm(i)];
> plot2d4(x,y) //Векторы UL
> x=[0 (UL_Re(i)+UR_Re(i))];
> y=[0 (UL_Jm(i)+UR_Jm(i))];
> plot2d4(x,y) //Вектор U
> x1=UL_Re(i):0.1*UR_Re(i):(UL_Re(i)+UR_Re(i));
> y1=a1(i)+b1(i).*x1;
> plot(x1,y1,'b--')
> x2=UR_Re(i):0.1*UL_Re(i):(UL_Re(i)+UR_Re(i));
> y2=a2(i)+b2(i).*x2;
> plot(x2,y2,'b--')
> end
--> xtitle ("Векторная диаграмма напряжений для RL-цепи","Re, В","jJm, В") //Подписи графика и осей
--> //Координатная сетка
--> xgrid
--> //Почастотный вывод напряжений и их фаз
--> for i=1:N
> mprintf('f=%4.0f URmod=%5.4f arg_UR=%5.2f MU2=%5.4f arg_UL=%5.2f\n',f(i),URmod(i),arg_UR(i),MU2(i),arg_UL(i))
> end
f=1000 URmod=1.2674 arg_UR=3.69 MU2=0.0818 arg_UL=86.31
f=2000 URmod=1.2595 arg_UR=7.36 MU2=0.1626 arg_UL=82.64
f=3000 URmod=1.2468 arg_UR=10.96 MU2=0.2415 arg_UL=79.04
f=4000 URmod=1.2297 arg_UR=14.48 MU2=0.3175 arg_UL=75.52
f=5000 URmod=1.2086 arg_UR=17.89 MU2=0.3901 arg_UL=72.11
|
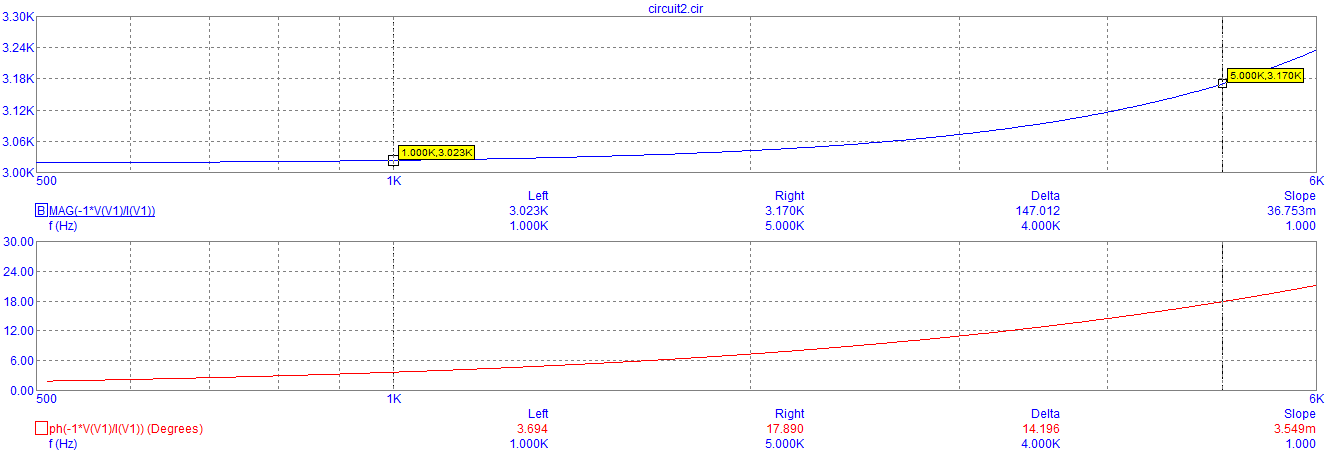
Графики зависимости модуля и фазы комплексного сопротивления RL-цепи от частоты
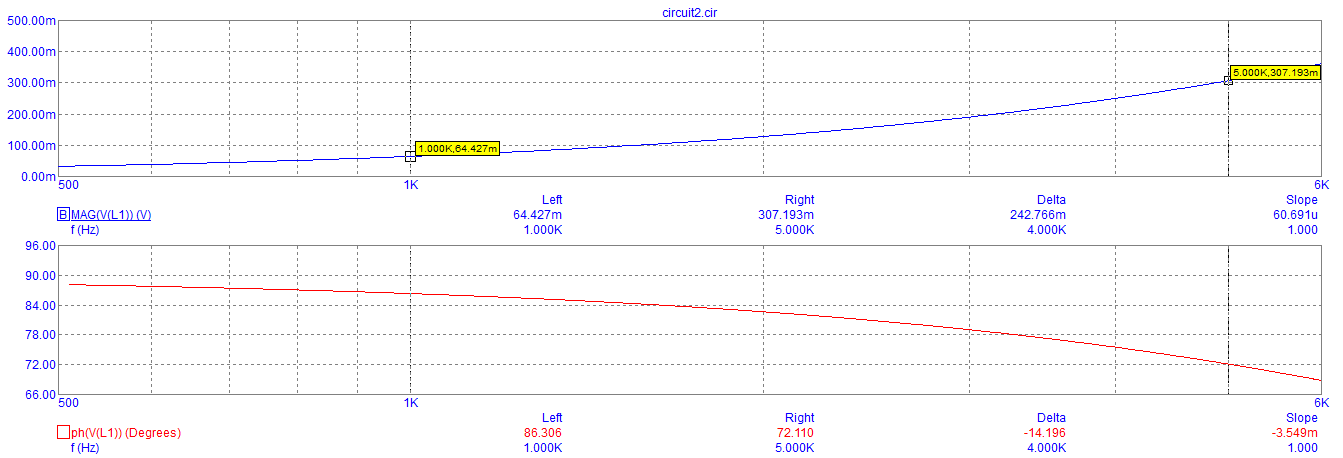
Графики зависимости модуля и фазы комплексного напряжения конденсатора RL-цепи от частоты
Выводы
Выполняя данную лабораторную работу, мы исследовали электрический режим конденсатора и катушки индуктивности в цепях гармонического тока, а также провели необходимые расчёты и построили графики зависимостей. По итогу лабораторной работы мы можем отметить, что результат предварительного расчета почти полностью совпадает с результатом машинного с учетом допустимой погрешности.
Ответы на вопросы
1) Какая частота называется граничной для RL-цепи?
Ответ: Частота, при которой вещественная часть входного комплексного сопротивления равна модулю его мнимой части. Она равна: 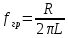
2) Каково значение модуля входного сопротивления RL-цепи на граничной частоте?
Граничная частота 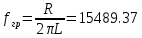 Гц. Модуль входного сопротивления равен: Гц. Модуль входного сопротивления равен: 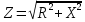 , где , где 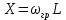 , , 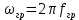 , тогда Z =4 266,6823 Ом , тогда Z =4 266,6823 Ом
Ответ: Z= 4 266,6823Ом
3) Каково значение аргумента входного сопротивления RL-цепи на граничной частоте?
Аргумент входного сопротивление находится по формуле: 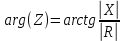 где где 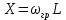 , а , а 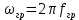 , тогда получаем arg(Z)=45° , тогда получаем arg(Z)=45°
Ответ: arg(Z)=45°
4) К чему стремится модуль тока RL-цепи при увеличении частоты?
Ответ: Модуль тока стремится к нулю.
5) Чему равен модуль входного сопротивления RL-цепи при частоте равной нулю?
Если f=0, тогда ω=0 (т.к.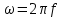 ). Модуль входного сопротивления ). Модуль входного сопротивления 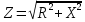 , где , где 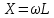 . Получается, что Z=R, а значит Z=3017 Oм . Получается, что Z=R, а значит Z=3017 Oм
Ответ: Z=3017 Oм
. |
|
|
 Скачать 337.59 Kb.
Скачать 337.59 Kb.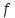 =1,2,3,4,5 кГц – частота;
=1,2,3,4,5 кГц – частота;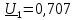 В – входное комплексное напряжение;
В – входное комплексное напряжение;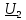 – выходное комплексное напряжение;
– выходное комплексное напряжение;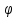 – сдвиг фазы;
– сдвиг фазы;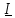 – комплексный ток;
– комплексный ток;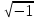 – мнимая единица;
– мнимая единица;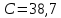 нФ – емкость конденсатора;
нФ – емкость конденсатора;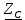 – комплексное сопротивление конденсатора;
– комплексное сопротивление конденсатора;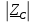 – модуль комплексного сопротивления конденсатора;
– модуль комплексного сопротивления конденсатора;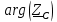 – фаза комплексного сопротивления конденсатора;
– фаза комплексного сопротивления конденсатора;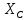 – ёмкостное сопротивление конденсатора;
– ёмкостное сопротивление конденсатора;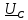 – комплексное напряжение на конденсаторе;
– комплексное напряжение на конденсаторе;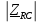 – модуль комплексного сопротивления RC-цепи;
– модуль комплексного сопротивления RC-цепи;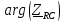 – фаза комплексного сопротивления RC-цепи;
– фаза комплексного сопротивления RC-цепи;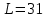 мГн – индуктивность катушки;
мГн – индуктивность катушки;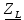 – комплексное сопротивление катушки;
– комплексное сопротивление катушки;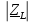 – модуль комплексного сопротивления катушки;
– модуль комплексного сопротивления катушки;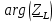 – фаза комплексного сопротивления катушки;
– фаза комплексного сопротивления катушки;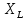 – индуктивное сопротивление катушки;
– индуктивное сопротивление катушки;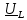 – комплексное напряжение на катушке;
– комплексное напряжение на катушке;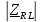 – модуль комплексного сопротивления RL-цепи;
– модуль комплексного сопротивления RL-цепи;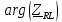 – фаза комплексного сопротивления RL-цепи;
– фаза комплексного сопротивления RL-цепи;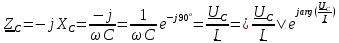 - комплексное сопротивление конденсатора;
- комплексное сопротивление конденсатора;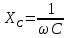 – ёмкостное сопротивление конденсатора;
– ёмкостное сопротивление конденсатора;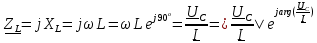 – комплексное сопротивление катушки;
– комплексное сопротивление катушки;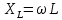 – индуктивное сопротивление катушки;
– индуктивное сопротивление катушки;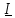 =
=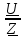 – комплексный ток;
– комплексный ток;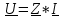 – комплексное падение напряжения;
– комплексное падение напряжения;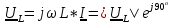 – комплексное напряжение на катушке;
– комплексное напряжение на катушке;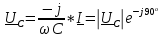 – комплексное напряжение на конденсаторе.
– комплексное напряжение на конденсаторе.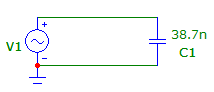














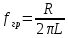
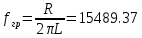 Гц. Модуль входного сопротивления равен:
Гц. Модуль входного сопротивления равен: 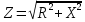 , где
, где 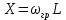 ,
, 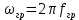 , тогда Z =4 266,6823 Ом
, тогда Z =4 266,6823 Ом 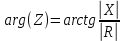 где
где 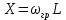 , а
, а 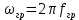 , тогда получаем arg(Z)=45°
, тогда получаем arg(Z)=45°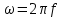 ). Модуль входного сопротивления
). Модуль входного сопротивления 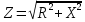 , где
, где 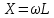 . Получается, что Z=R, а значит Z=3017 Oм
. Получается, что Z=R, а значит Z=3017 Oм
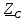 , Ом
, Ом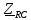 ,Ом
,Ом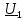 ,В
,В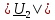 ,В
,В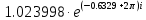
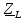 , Ом
, Ом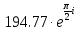
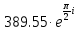
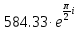
 ,Ом
,Ом