Курсовая работа. записка. Н. Э. Баумана Факультет "Робототехники и комплексной автоматизации" Кафедра "Теории механизмов и машин" расчетнопояснительная записка

• Название: Н. Э. Баумана Факультет "Робототехники и комплексной автоматизации" Кафедра "Теории механизмов и машин" расчетнопояснительная записка
• Анкор: Курсовая работа
• Дата: 25.03.2023
• Размер: 0.87 Mb.
• Имя файла: записка.doc
• Тип: Реферат; #1014121
• страница: 2 из 3

2.Определение закона движения звена приведения при установившемся режиме работы машинного агрегата.
Определение размеров звеньев механизма:

2.1. Определяем размеры кривошипа по формуле: l1 = lAO = (15*Vср) / n1, м.

(где n1 – число оборотов в минуту кривошипа).

l1 = lAO = (Vср) / 4*n1.

l1 = lAO =2.5 / 4*6.5=0.096м.
2.2. Выбираем масштаб изображения кинематической схемы механизма в положении, заданном в техническом задании.

Следует иметь в виду, что ход поршня равен двум длинам кривошипа. Следовательно, можно до определения размера кривошипа задаться его длиной в миллиметрах. Пусть

AB = 48 мм, тогда ход поршня H = 96 мм. Длина шатуна на чертеже определяется из пропорции: lAB = λ₂* lAO, мм. Масштаб изображения кинематической схемы на чертеже равен: µl = AB / lAO, мм/м.

lAB = 4.5*96 = 432 мм

µl = 48 / 0.096 = 500 мм/м.

µl = 500 мм/м.
Построение индикаторной диаграммы:

2.3. В пределах отрезка H – хода поршня строим индикаторную диаграмму по данным таблицы технического задания (по заданному максимальному значению давления в цилиндре двигателя). Для этого длина отрезка H – (ось абсцисс является одновременно линией атмосферного давления) разбивается на десять равных частей. Каждая часть отмечается долей 0.1, 0.2, 0.3,…1.0.Изменение давления задано в техническом задании в виде отношения текущего давления Pi к максимальному давлению Pmax. Поэтому необходимо задаться на чертеже отрезком Ypmax = 100 мм, провести через точки 0.1, 0.2, 0.3,…1.0 отрезки, параллельные оси ординат, и отложить на каждом из них последовательно ординаты в миллиметрах: Ypi = Ypmax*Pi/ Pmax, мм. Полученные точки соединяют плавной кривой.

Масштаб индикаторной диаграммы µp, мм/Па – равен отношению Ypmax = 100мм к заданной максимальной величине Pmax.
µp = 100 / (10^7) = 0.00001 мм/Па.
µp = 0.00001 мм/Па.
Построение графика сил:

2.4. Построение графика сил, действующих на поршень поршневой машины.

Ординаты графика сил выбираем равными ординатам индикаторной диаграммы. Тогда масштаб графика сил по оси ординат равен: µF = µp / Sп, мм/Н. Здесь Sп –площадь поршня. Sп = (π*d^2) / 4, м^2. (d – диаметр цилиндра поршневой машины).

График сил строится с учетом знака силы.

Sп = (3.14*0.08^2) / 4 = 5.02*10^(-3) м^2.

Sп = 5.02*10^(-3) м^2.

µF = 0,00001 / [5.02*10^(-3)] = 0.00199 мм/Н.

µF = 0.00199 мм/Н.
Определение передаточных функций и передаточного отношения:

2.5.Определяем кинематические параметры механизма: функции положения подвижных точек механизма S_C = f(f₁), S_S2 = f(f₁ ),передаточные функции V_qb= f(f₁ ), V_qs2 = f(f₁ )(аналоги линейных скоростей подвижных точек механизма), передаточное отношение U₂₁= f(f₁).

Указанные параметры определяем,построив графическим способом планы скоростей для шести положений механизма (от 0 до 6) и определяя кинематические параметры, замеряя соответствующие отрезки с планов скоростей и беря их соотношения. Значения параметров заносим в таблицу 1, которая будет приведена ниже.

По полученным данным строим соответствующие зависимости (рис.1).
Графики приведенных моментов инерции и суммарного приведенного момента инерции второй группы звеньев:

2.6.Строятся графики приведенных моментов инерции второй группы звеньев.

Величины приведенных моментов рассчитываем по формулам:

Приведенный момент инерции поршня I^пр_3n=m₃ *(lAO)^2* (p_vb/p_va)^2 _,кгм^2.

Приведенный момент инерции шатуна в поступательном движении I^пр_2n = m₂*(lAO)^2* (p_vs2/ p_va)^2 _,кгм^2.

Приведенный момент инерции шатуна во вращательном движении I^пр_2вр=I_S2 *(lAO/ lBA)^2* (ab/ p_va)^2 _,кгм^2.

Все кривые строят в одном масштабе , который определяется как отношение Y I^пр_3n (задается приблизительно 100мм) к максимальному значению I^пр_{3n :}

µI = Y I^пр_3n /I^пр_3n = 100/0.276= 362.3 мм/ кгм^2.

µI= 362.3 мм/ кгм^2.

Результаты расчета по указанным выше формулам заносим в таблицу 1.

По данным расчета строим три кривые I^пр_3n =f(f₁ ) , I^пр_2n = f(f₁ ), I^пр_2вр= f(f₁ ), которые затем графически складываем в каждой позиции от 0 до 12 и получаем кривую суммарного приведенного момента инерции второй группы звеньев в первом цилиндре I^прS _II. Масштаб по оси f₁ : µf= 38.2 мм/рад.

В нашем техническом задании механизм имеет два цилиндра, и каждый из них имеет одинаковые размеры ,но процесс во втором смещен относительно процесса в первом на 180 градусов, поэтому для получения суммарного приведенного момента инерции второй группы звеньев второго цилиндра, необходимо кривую суммарного момента второй группы звеньев первого цилиндра сместить на заданный угол. Затем обе суммарные кривые еще раз суммируем на том же графике и получаем значения суммарного приведенного момента инерции второй группы звеньев для двух цилиндров.
Построение графика приведенного момента от движущих сил и суммарного приведенного момента от сил для двух цилиндров:

2.7. Строим график приведенного момента от сил, действующих на поршень поршневой машины (для двух цилиндров).

Расчет приведенного момента осуществляют по формуле:

Мпр = F*VqB, H*м.
Можно подсчитать приведенный момент и по более развернутой формуле:
Мпр = lAO *(YF/ µF)* (p_VB/ p_VA), Нм.

Здесь lAO – длина кривошипа в метрах, YF - ордината графика сил в соответствующей позиции точки «B» поршня в миллиметрах, µF - масштаб графика сил в мм/Н, p_VB -отрезок с плана скоростей, соответствующий скорости точки «B» поршня, p_VA - отрезок с плана скоростей, соответствующий скорости точки «A» кривошипа.

Результаты расчетов заносим в таблицу 2, которая будет приведена ниже.

Получив в таблице наибольшую величину приведенного момента, задаемся произвольной величиной отрезка YМmax = 100мм, который будет изображать эту максимальную величину Mпр, max на графике. Тогда масштаб графика по оси ординат:

µМ = YМmax / Mпр, max, мм/Нм.

µМ = 100 / 4557 = 0.022 мм/Нм.

µМ = 0.022 мм/Нм.

Так как механизм имеет два цилиндра и индикаторная диаграмма для них обоих одинакова, то график приведенного момента от сил для второго цилиндра будет смещен относительно графика для первого цилиндра на фазовый угол, данный в техническом задании: φ = π рад. Суммируем два полученных графика и получаем график суммарного приведенного момента от сил для двух цилиндров.
Построение графика работы движущих сил и графика суммарной работы:

2.8. Методом графического интегрирования строим график работы движущих сил АД; интегрируемая кривая – МД,пр = f(f₁ ), суммарная для двух цилиндров.

Чтобы осуществить графическое интегрирование кривой,на продолжении оси f₁ выбираем произвольный отрезок интегрирования ОК = 50 мм.

Как известно, при установившемся режиме работы машинного агрегата, работа движущих сил за цикл должна равняться работе сил сопротивления. Этот факт учитывается при определении приведенного момента сил сопротивления. В позиции 12 получают работу движущих сил или работу сил сопротивления за цикл при установившемся режиме работы в зависимости от того, какой график получен – работы движущих сил или работы сил сопротивления.

В первом приближении можно считать, что момент сопротивления постоянен за цикл работы машинного агрегата. Следовательно, график работы сил сопротивления имеет вид наклонной линии, начальной точкой которой является ноль, а конечной ордината YA12, отложенная со знаком минус. Для получения графической зависимости МС,пр = f(f₁ ) из точки К отрезка интегрирования ОК проводят линию, параллельную наклонной прямой АС = f(f₁ ) до пересечения с осью ординат графика МД,пр = f(f₁ ). Из полученной точки пересечения проводят линию, параллельную оси f₁ – это и есть зависимость МС,пр= f(f₁ ). Для получения численного значения замеряют ординату YMC в миллиметрах и делят полученную величину на масштаб графика приведенного момента от сил, действующих на поршень µМ, мм/Нм.

YMC = 32.98 мм.

МС,пр = 32.98 / 0.022 = 1499 Hм.

Строим график суммарного приведенного момента сил, подняв ось f₁ на величину YMC на графике МД,пр = f(f₁ ).
2.9. Строим график суммарной работы АΣ= f(f₁ ). Для этого графически складываем графики АΣД = f(f₁ ) и АΣС = f(f₁ ) с учетом их знаков.

Масштаб графика работы определяют по формуле: µА = (µМ* µf) / OK, мм / Дж.

µА = (0.022*38.2) / 50 = 0.0168 мм / Дж.

µА = 0.0168 мм / Дж
Построение графика угловой скорости:

2.10.Определение закона движения звена приведения одномассной динамической модели.

В первом приближении суммарный график приведенных моментов инерции второй группы звеньев принимаем за график кинетической энергии второй группы звеньев T_II = f(f₁ ), который построен в масштабе:

µT= 2* µI /(w_1cр )^2.

Средняя угловая скорость подсчитывается по формуле: w_1cр= π*n₁/30 (здесь число оборотов n₁ обязательно подставляется в об/мин).

w_1cр= 3.14*390/30= 40.84 рад/c.

µT= 2*362.3/(40/84)^2= 0.434 мм/Дж.

µT= 0.434 мм/Дж.
Построим графическую зависимость T_II = f(f₁ ) в масштабе µT и пересчитаем ее в масштаб графика суммарной работы µА. Для определения величины ординат Y_III= Z_i (Z_i- ординаты на графике кинетической энергии) в масштабе µА необходимо взять отношение масштабов µА/ µT=k. Затем умножить k на Z_i .Результаты этого произведения обозначим B_i в миллиметрах и занесем в таблицу 3.

Примем Y_Tнач = 40мм. Опустив ось f₁ на величину Y_Tнач , получим ось f^*_1, относительно которой будет построен график суммарной кинетической энергии машинного агрегата TS= f(f₁ ).Вычитая из ординат кривой TS= f(f^*₁ ) значения B_i получим кривую T_I= f(f^*₁ ), которая и есть графическая зависимость угловой скорости w₁= f(f^**₁ ), построенная относительно оси f^**₁ в масштабе µw= µА*w_1cр*I^пр _{I_необх} , мм/радc^(-1).

I^пр _{I_необх} = D T_{I_max} / ((w_1cр )^2)* d , кгм^2.

D T_{I_max} = Y_{TI_max} / µА , Дж.

Y_{TI_max} = Y_TImax- Y_TImin = 30.78 мм.
D T_{I_max} = 30.78/ 0.0168 = 1832.1 Дж.
I^пр _{I_необх} = 1832.1/ ((40.84)^2)*(1/28) = 30.75 кгм^2/рад^2.
µw= 0.0168*40.84*30.75= 21.09 мм/радc^(-1).

µw= 21.09 мм/радc^(-1).

Yw1ср = w_1cр* µw= 40.84*21.09= 861.31мм.

Yw1ср= 861.31мм.

Определение углового ускорения звена приведения:

Угловое ускорение звена приведения определяем только для одной позиции ,которая задана углом f₁ для силового расчета в таблице технического задания.

Формула для расчета углового ускорения имеет вид:
e_i = M^прS _i/ I^прS _i – ((w_i)^2/2*I^прS _i)* dI^прS _i/df₁

M^прS _i= f(f₁ ) = M^прS ₂– M^прс= 4446–1499= 2947 Нм.
I^прS _i= I^пр _{I_необх} =30.75 кгм^2/рад^2.
Ywi= Yw2= Yw1ср-YDw2= 861.31-1.88= 859.43 мм.

w_i= w₂ = 40.75 рад/с.
dI^прS _i/df₁= dI^пр _II/df₁= (µf/ µI)*tgy_k .

tgy_k= AK/100, AK= 78.5мм, tgy_k= 78.5/100=0.785.

dI^прS _i/df₁=(µf/ µI)*tgy_k=( 38.2/ 362.3)*0.785= 0.083 кгм^2/рад.


e_i= e₂= 2947/30.75–((40.75)^2/2*30.75)*0.083= 93.59 рад^2/с^2.

e₂= 93.59 рад^2/с^2.

3. Силовой расчет механизма.
Для рассчитываемого положения механизма

Из первого листа находим для этого положения



Силы, действующие на поршень: ,
Построение плана скоростей для точек механизма в заданном положении:











Построение плана ускорений точек механизма в заданном положении: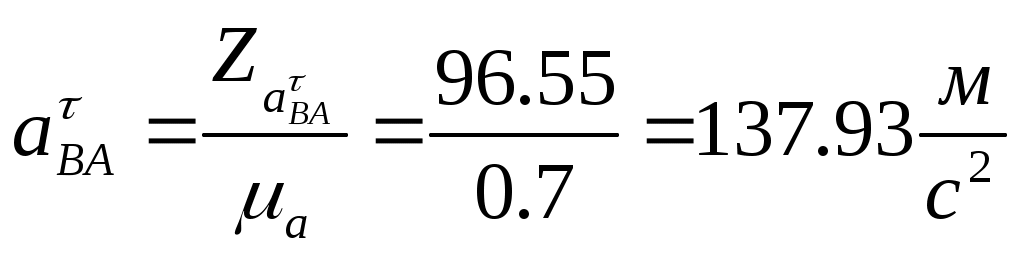
















Для шатуна 2: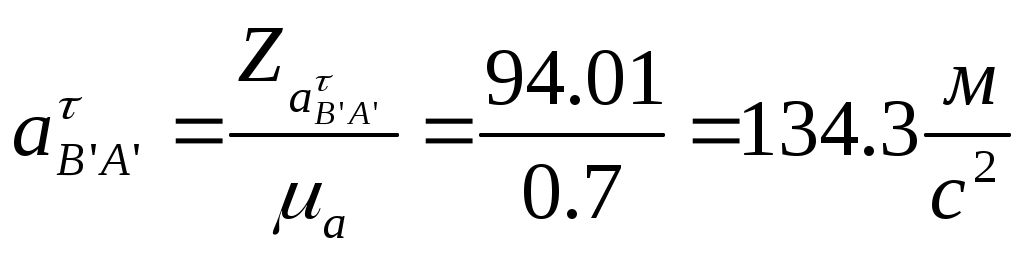



















Для шатуна 4:


Определение главных векторов и главных моментов сил инерции:













Определение сил тяжести звеньев:




Для первого звена масса не задана, значит, его весом пренебрегаем.

Силовой расчет механизма:
Запишем уравнение Даламбера для третьего звена:



Рассмотрим отдельно звено 2:



Так как звено находится в равновесии, то можем записать









Запишем уравнение Даламбера для группы звеньев 2-3:



В уравнении два неизвестных, значит его можно решить. Строим план сил в масштабе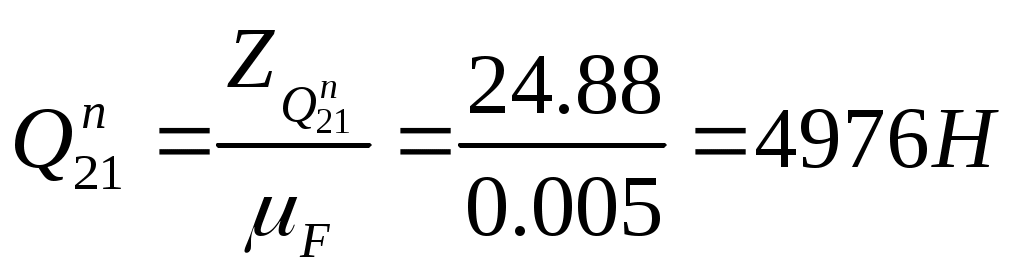







Теперь можно решить уравнение для звена 3:



Строим план сил в масштабе

Из чертежа находим
Запишем уравнение Даламбера для пятого звена:



Рассмотрим отдельно звено 4:



Так как звено находится в равновесии, то можем записать





-



Запишем уравнение Даламбера для группы звеньев 4-5:



В уравнении два неизвестных, значит его можно решить. Строим план сил в масштабе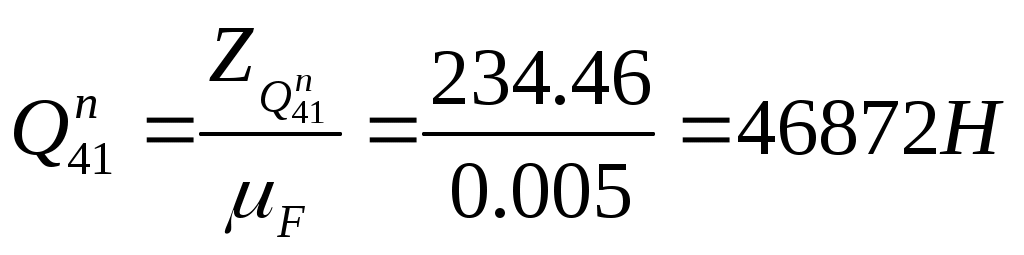







Теперь можно решить уравнение для звена 5:



Строим план сил в масштабе

Из чертежа находим
Запишем уравнение Даламбера для звена 1:



Строим план сил в масштабе

Из чертежа находим
Для нахождения момента сопротивления запишем уравнение равновесия первого звена:











Вычислим разницу:



4. Проектирование зубчатой передачи.
Расчет геометрических параметров зубчатой передачи: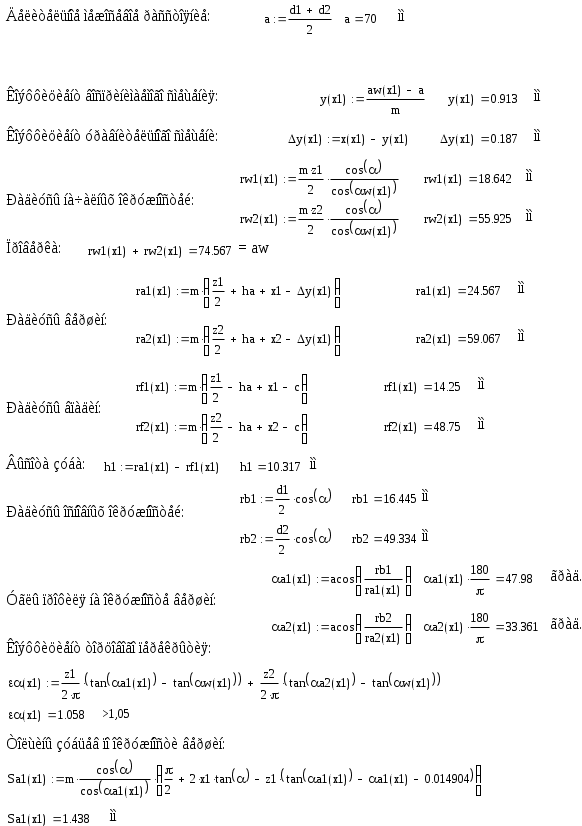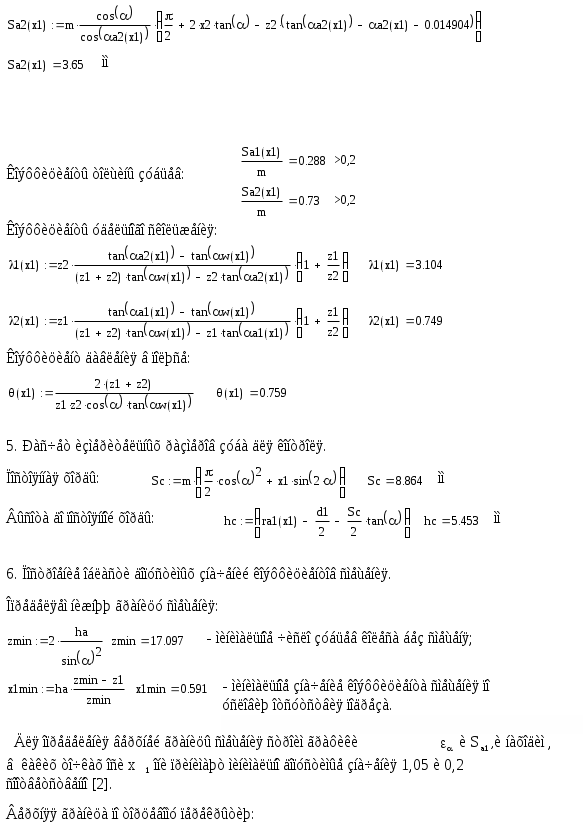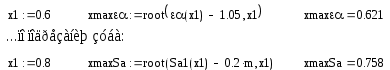





Построение профиля зуба колеса, изготовляемого реечным инструментом:

Профиль зуба колеса образуется как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. Такое образование профиля отражает реальный процесс изготовления колеса на станке. При этом эвольвентная часть профиля зуба образуется прямолинейной частью реечного производящего исходного контура, а переходная кривая профиля зуба - закругленным участком.

Схема станочного зацепления строится следующим образом:

1. 
   Проводится делительная d₁=d_W01 и основная d_b1 окружности, а также окружности вершин d_a1 и впадин d_f1.
   
2. 
   Откладывается от делительной окружности (с учетом знака) выбранное в результате анализа смещение x₁∙m и проводится делительная прямая исходного производящего контура реечного инструмента. На расстоянии вверх и вниз от делительной прямой проводятся прямые граничных точек, а на расстоянии - прямые вершин и впадин, станочно-начальная прямая Q-Q проводится касательно к делительной окружности в точке P₀ (полюс станочного зацепления).
   
3. 
   Проводится линия станочного зацепления N₁P₀ через полюс станочного зацепления P₀ касательно к основной окружности в точке N₁. Эта линия образует с прямыми исходного производящего контура инструмента углы, равные _W0= .
   
4. 
   Строится исходный производящий контур реечного инструмента так, чтобы ось симметрии впадины совпадала с вертикалью. Для этого от точки пересечения вертикали с делительной прямой (точка G) откладывается влево по горизонтали отрезок в 1/4 шага и через конец его перпендикулярно линии зацепления N₁P₀ проводится наклонная прямая, которая образует угол  с вертикалью. Эта прямая является прямолинейной частью профиля зуба исходного производящего контура инструмента. Закругленный участок профиля строится как сопряжение прямолинейной части контура с прямой вершин или прямой впадин окружностью радиусом _f. Симметрично относительно вертикали P₀G (линия симметрии впадин) cтроится профиль второго зуба исходного производящего контура, прямолинейный участок которого перпендикулярен к другой возможной линии зацепления: P₀N₁^´. Расстояние между одноименными профилями зубьев исходного контура равно шагу .
   

5. 
   Строится профиль зуба проектируемого колеса, касающийся профиля исходного производящего контура в точке К. Для построения ряда последовательных положений профиля зуба исходного производящего контура проводится вспомогательная прямая MM касательно к окружности вершин. Фиксируются точка пересечения линии MM и прямолинейной части профиля инструмента W и центр окружности закругленного участка профиля - точку L. Откладываются на прямой MM несколько отрезков равной длины 20 мм и отмечаются точки I, II, III, IV, V и т.д.. Отложим 11 точек. Такие же отрезки откладываются на станочно-начальной прямой Q-Q (точки 1, 2, 3, ...) и на дуге делительной окружности (точки ...). Из центра О₁ колеса через точки ... на делительной окружности проводят лучи ... до пересечения с окружностью вершин в точках ... . При перекатывании без скольжения станочно-начальной прямой по делительной окружности точки 1,2,3,... и точки ... последовательно совпадают; то же для точек I, II, III, ... и точек ... . При этом точка W описывает укороченную эвольвенту, а точка L - удлиненную. Любое промежуточное положение точки W или L находится построением соответствующих треугольников. Например, для положения 2 берется треугольник II-2-W, размеры которого при обкатке сохраняются. Когда точка 2 совпадает с точкой , сторона II-2 пойдет по лучу и займет положение стороны -2. Тогда точка W_II определится как положение вершины треугольника, построенного методом засечек по известным сторонам ( ; ; ), т.е. треугольник W-II-2 займет положение треугольника . Аналогично находится положение точки L₂. Из точки L₂ радиусом _f проводится окружность, а через точку W_II касательно к этой окружности - прямая, которая дает новое (второе) положение исходного производящего контура. Все последующие положения (W_III,W_IV,W_V и т.д.) строятся аналогично. К полученному ряду положений профиля зуба исходного контура проводится огибающая, которая определяет левый профиль зуба изготовляемого колеса. Затем на окружности вершин откладывается толщина зуба S_a1. Через концы отложенных отрезков, строится вторая половина этого же зуба. На изготовляемом колесе строим несколько зубов. Для этого откладывается от вертикали в обе стороны шаг по хорде делительной окружности . Через концы этих отрезков и центр колеса O₁ проводятся линии симметрии правого и левого зубьев, по отношению к которым строятся зубья колеса. При правильном построении зацепления эвольвенты, очерчивающие профиль зубьев нарезаемых колес, должны касаться прямолинейной части профиля инструмента на линии зацепления (в точках K₁ и K₁^´).
   

Построение проектируемой зубчатой передачи:

1. 
   Откладывается межосевое расстояние a_W и проводятся окружности: начальные d_W1,d_W2 ; делительные d₁,d₂; основные d_b1,d_b2; окружности вершин d_a1,d_a2 и впадин d_f1,d_f2. Начальные окружности должны соприкасаться в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно воспринимаемому смещению y∙m_t. Расстояние между окружностями вершин одного колеса и впадин другого, измеренное по осевой линии, должно быть равно радиальному зазору c_t*∙m_t.
   
2. 
   Через полюс зацепления касательно к основным окружностям колес проводится линия зацепления. Точки касания N₁ и N₂ называются предельными точками линии зацепления. Линия зацепления образует с перпендикуляром, восстановленным к осевой линии в полюсе, угол зацепления _W . Буквами B₁ и B₂ отмечена активная линия зацепления. Точка B₁ является точкой пересечения окружности вершин колеса с линией зацепления, ее называют точкой начала зацепления; точка B₂ − точка пересечения окружности вершин шестерни с линией зацепления, ее называют точкой конца зацепления.
   
3. 
   На каждом колесе строятся профили трех зубьев, причем точка контакта К должна располагаться на активной линии зацепления. Профили зубьев шестерни перенесены на чертеж проектируемой передачи со схемы станочного зацепления с помощью шаблона; эвольвентная часть профиля зуба колеса строится обычным образом, как траектория точки прямой при перекатывании ее по основной окружности без скольжения, и переносится в точку контакта зубьев К на линию зацепления. От построенного профиля зуба откладывается толщина зуба по делительной окружности и проводится аналогичный профиль другой стороны зуба. Профили двух других зубьев располагаются на расстоянии шага . На зубьях, соприкасающихся в точке К, отмечаются активные профили, которые взаимодействуют в процессе зацепления. Нижние точки активных профилей лежат на пересечении окружностей d_p1 и d_p2 соответствующих профилей. Активные профили перекатываются друг по другу со скольжением, поэтому их длины различны.
   

Проектирование планетарного зубчатого механизма:
Исходные данные:

1. Число сателлитов в редукторе к=3,

2 . Модуль зубчатых колес m=5;

3. Передаточное отношение редуктора
Задан планетарный однорядный механизм.

Входное звено – звено 8;

Выходное – водило.
Подбор чисел зубьев.
Если бы ось в планетарном механизме стала неподвижной, то мы могли бы записать:

(1)

Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь:

8 звено: ω^*₈ = ω₈ + (–ω_н)

7 звено: ω^*₇ = ω₇ + (–ω_н)= –ω_н

6 звено: ω^*₆ = ω₆ + (–ω_н)

ω^*_н = ω_н + (–ω_н) = 0 , тогда из уравнения (1) получим



если (1) переписать через количество зубьев, то

(здесь минус, так как зацепление внешнее), тогда уравнение передаточного отношения будет

- плюсовой механизм (2)

Подставим в уравнение (2) значения передаточного числа для заданного механизма:



Зададимся числом зубьев z₈ так, чтобы отсутствовал подрез у зубчатых колес и

числа зубьев были целыми , т.е. z₈  18 и z₇  85, тогда z₈ = 72,

z₇ = 1.5 ^. 72 = 108 ≥ 85.

Заклинивания нет, z₇ – z₈ =108-72=36≥8.
Из условия соосности, которым определяется соосное расположение центральных колес планетарного механизма с водилом h, следует равенство межосевых расстояний зацепляющих колес:

r₈ + r₆ = r₇ – r₆



z₈ + z₆ = z₇ – z₆



Проверим выполнение условий соседства и сборки:

1. 
   Уравнение условия соседства имеет вид: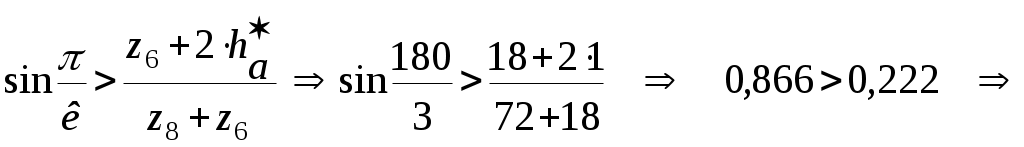
   

условие соседства выполнено.

2. 
   Уравнение условия сборки имеет вид: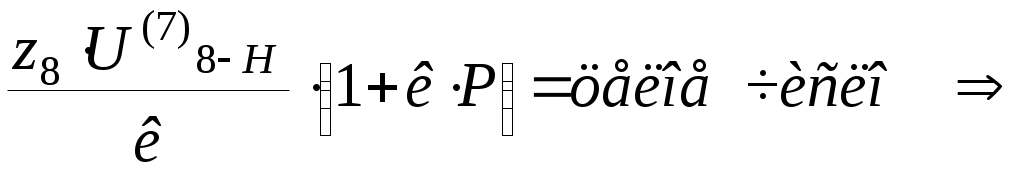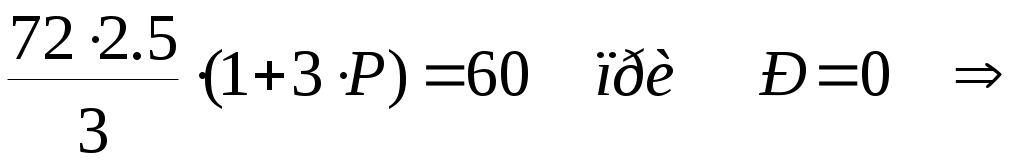
   

условие сборки выполнено.
Проверка передаточного отношения планетарного зубчатого механизма графическим способом: