|
ТВзачет. На один ряд из 7 мест, случайным образом садятся 7 учеников. Найти вероятность того, что три определенных ученика окажутся рядом в магазине имеется в продаже 20 пар обуви, из которых 7 пар 42 размера
На один ряд из 7 мест, случайным образом садятся 7 учеников. Найти вероятность того, что три определенных ученика окажутся рядом
|
В магазине имеется в продаже 20 пар обуви, из которых 7 пар 42 размера. Найти вероятность того, что из 8 -ми покупателей 3 выберут обувь 42 размера.
|
На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,2% брака; второй - 0,3% и третий - 0,4%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 500, со второго - 1000 и с третьего - 1500 деталей.
|
Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найти вероятность, что их произведение будет не больше 1, а частное y/x не больше двух.
|
Однотипные приборы выпускаются тремя заводами в количественном отношении 1:2:3, причем вероятности брака для этих заводов соответственно равны 3%; 2%; 1%. Прибор, приобретенный НИИ, оказался бракованным. Какова вероятность того, что этот прибор произведен первым заводом (марка завода на приборе отсутствовала)
|
Наудачу взяты два положительных числа x и y, каждое из которых не превышает 1. Найти вероятность того, что их сумма не превышает 1, а произведение не меньше 0,09.
|
В прямоугольник с вершинами K(-1,0), L(-1,5),M(2,5), N(2,0) брошена точка. Какова вероятность того,что её координаты будут удовлетворять неравенствам
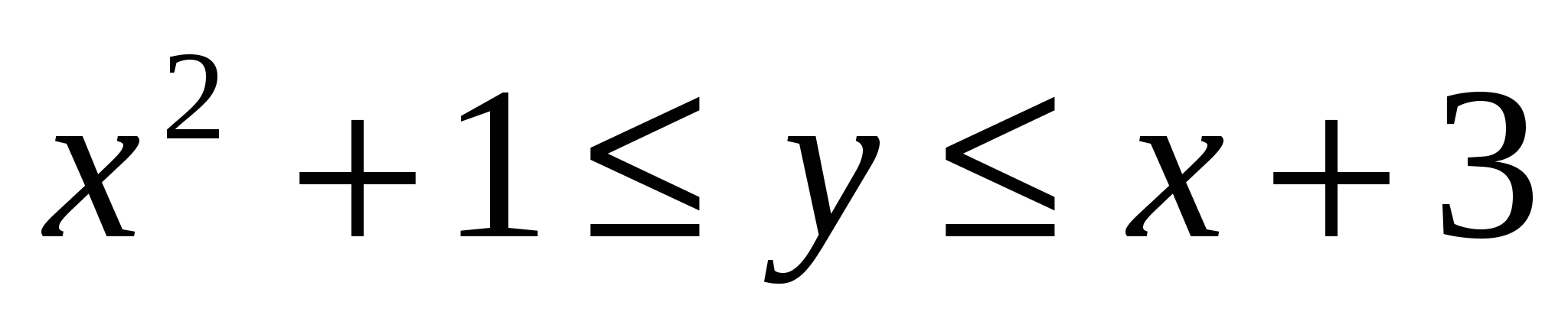
|
В семье 5 детей. Считая вероятность рождения мальчика и девочки одинаковыми, найти вероятность того, что среди этих детей: а) 2 мальчика; б) не более 2-х мальчиков; в) более 2-х мальчиков.
|
Внутри квадрата построен равносторонний треугольник со стороной, равной стороне квадрата. В квадрат бросается точка. С какой вероятностью она попадёт в треугольник?
|
Найти вероятность того, что абонент наберет правильный двузначный номер, если он знает, что данный номер не делится на 5.
|
Случайная величина X задана интегральной функцией:
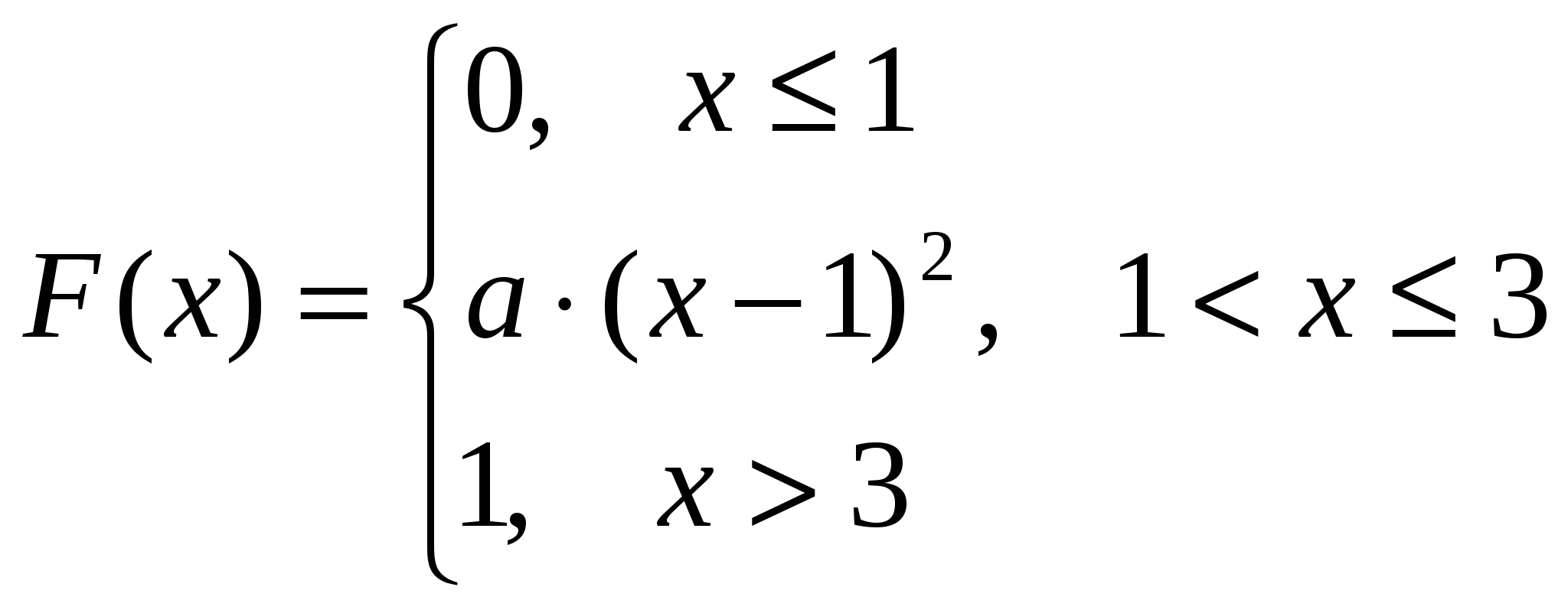
Найти:
Значение a,
Математическое ожидание,
P(1,2)
Построить графики функций распределения.
|
ДСВ X задана законом распределения
-
X
|
1
|
3
|
5
|
7
|
9
|
P
|
0,2
|
0,25
|
0,3
|
0,15
|
0,1
|
Построить многоугольник распределения, найти функцию распределения, построить график, найти математическое ожидание, дисперсию и среднее квадратическое отклонение ДСВ X.
|
На спортивных соревнованиях вероятность показать спортивный рекорд для первого спортсмена равна 0,5; для второго - 0,3; для третьего - 0,1. Какова вероятность того что: а) рекорд будет установлен одним спортсменом; б) рекорд будет установлен хотя бы одним спортсменом; в) рекорд не будет установлен.
|
Совокупность семей имеет следующее распределение по числу детей:
X
|
x1
|
x2
|
2
|
3
|
P
|
0,1
|
p2
|
0,4
|
0,35
|
Определить x1, x2, p2, если известно, что M(X)=2, D(X)=0,9.
|
Партия электролампочек на 25% изготовлена первым заводом; на 35% - вторым; на 40% - третьим. Вероятности выпуска бракованных лампочек соответственно равны: 0,03; 0,02; 0,01. Какова вероятность того, что наудачу взятая лампочка окажется бракованной?
|
ДСВ X задана законом распределения
-
X
|
1
|
3
|
5
|
7
|
9
|
P
|
0,05
|
0,15
|
0,2
|
0,4
|
0,2
|
Построить многоугольник распределения, найти функцию распределения, построить график, найти математическое ожидание, дисперсию и среднее квадратическое отклонение ДСВ X.
|
ДСВ X задана законом распределения:
X
|
1
|
x2
|
x3
|
8
|
P
|
0,1
|
p2
|
0,5
|
0,1
|
Определить x2, x3, p2, если известно, что M(X)=4, M(X2)=20,2.
|
Расследуются причины неудачного запуска космической ракеты, о котором можно высказать четыре гипотезы Hi,H2,Hj,H4. По данным статистики P(Hi)=0,2, Р(Н2)=0,4, Р(Н3)=0,3, Р(Н4)=0,1. В ходе расследования обнаружено, что произошла утечка топлива (событие А).
Условные вероятности события А согласно той же статистике равны: Р(А/ Н=0,9, Р(А/ Н2)= 0,4, Р(А/ Н3)=0,2, Р(А/ Н4)=0,3. Какая из гипотез наиболее вероятна при данных условиях?
|
Найти вероятность того, что при четырех подбрасываниях игральной кости 5 очков появится: а)2 раза, б) хотя бы 1 раз.
|
На участке А-В для мотоциклиста-гонщика имеется 3 препятствия, вероятность остановки на каждом из них равна 0.1. Вероятность того, что от пункта В до конечного пункта С мотоциклист проедет без остановки равна 0.7. Найти вероятность того, что на участке А-С не будет ни одной остановки.
|
Числа I, 2, 3, 4, 5 написаны на 5 карточках. Наудачу последовательно выбираются 3 карточки, и вынутые таким образом цифры ставятся слева направо. Найти вероятность того, что полученное при этом трехзначное будет четным..
|
Устройство состоит из 5 элементов, среди которых 2 изношенных. При включении устройства случайным образом включаются 2 элемента. Найти вероятность того, что включенными окажутся изношенные элементы.
|
Принимаем вероятность рождения мальчика и девочки равными. Найти вероятность того, что среди 10 новорожденных 6 окажутся мальчиками.
|
В ящике находятся 12 деталей, изготовленных на заводе 1, 20 деталей на заводе 2 и 18 деталей на заводе 3. Вероятность того, что деталь, изготовленная на заводе 1, отличного качества равна 0,9; для деталей изготовленных на заводах 2 и 3 эти вероятности равны 0,6 и 0,9. Наудачу берется деталь. Найти вероятность того, что она окажется отличного качества.
|
Какова вероятность того, что наудачу вырванный листок из нового календаря соответствует первому числу месяца? (Год считается не високосным)
|
Вероятность попадания в цель 1-м стрелком равна 0,7; вторым-0,5; третьим - 0,4. Найти вероятность того, что хотя бы один стрелок попадет в цель.
|
На фабрике, изготавливающей болты, первая машина производит 30%, вторая - 25%, третья - 45% всех изделий. Брак в их продукции составляет соответственно 2%; 1%; 3%. Найти вероятность того, что случайно выбранный болт окажется стандартным.
|
Вероятность выбора отличника на факультете равна 1/7. Из 28 студентов группы на удачу вызываются три студента. Определить вероятность всех возможных значений числа отличников, которые могут оказаться среди вызванных 3-х студентов.
|
Из ящика, в котором содержится 5 белых и 7 красных шаров, вынимают наугад три шара без возвращения. Какова вероятность, что среди вынутых шаров будет 2 белых и один красный?
|
В первом ряду аудитории 6 парт. За эти парты всегда садятся 6 друзей - студентов. Какова вероятность того, что при случайной посадке за эти парты Саша и Марина окажутся рядом?
|
Три стрелка стреляют по мишени по одному разу. Вероятность попадания в мишень первым стрелком равна 0.7, вторым - 0.8, третьим -0.9. Найти вероятность того, что мишень будет поражена (а) одной пулей, (б) двумя пулями, (в) хотя бы одной пулей.
|
В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность поражения мишени при выстреле из винтовки с оптическим прицелом равна 0.95, без оптического прицела - 0.7. Найти вероятность поражения мишени, если стрелок произведет один выстрел из наудачу взятой винтовки.
|
Детали изготавливаются на 3 станках, причем на первом станке изготавливается 50 % всех деталей, на втором 20%, остальные на третьем. Вероятность брака на первом станке - 0.03, на втором - 0.025, на третьем -0.01. Взятая наугад деталь оказалась бракованной. Найти вероятность того, что она изготовлена на втором станке.
|
Вероятность появления события в каждом из независимых испытаний равна 0.4. Найти вероятность того, что в серии из 500 опытов событие наступит (а) 250 раз, (б) менее 200 раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х- числа появлений события А в серии.
|
Два студента условились встретиться в определенном месте во время перерыва в между 13ч и 13ч 50 мин. Пришедший первым ждет другого в течение 10 мин., после чего уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанных 50 мин. Может произойти наудачу и моменты прихода независимы?
|
Случайная величина X задана интегральной функцией:
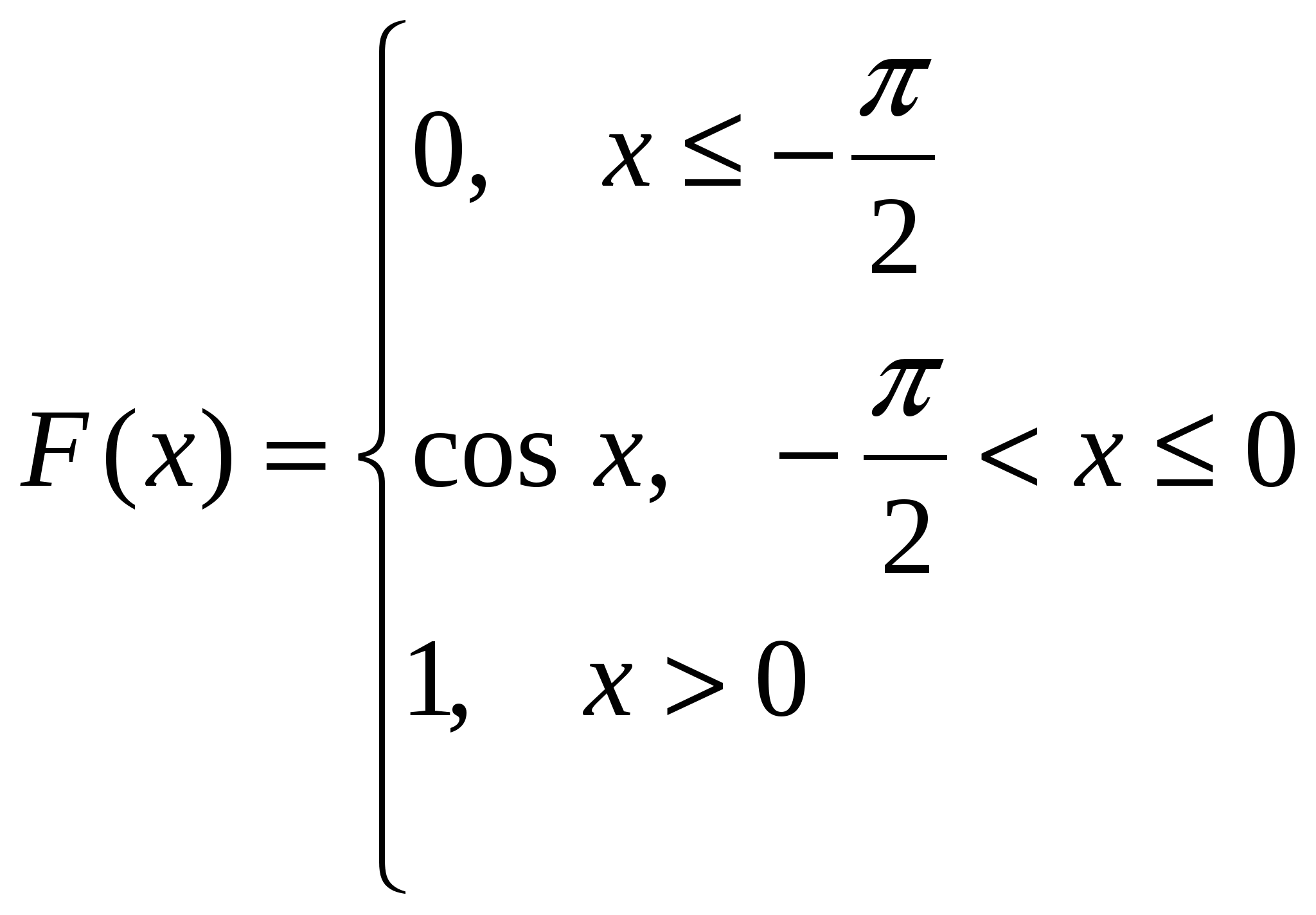
Найти:
Плотность распределения f(x),
Математическое ожидание,
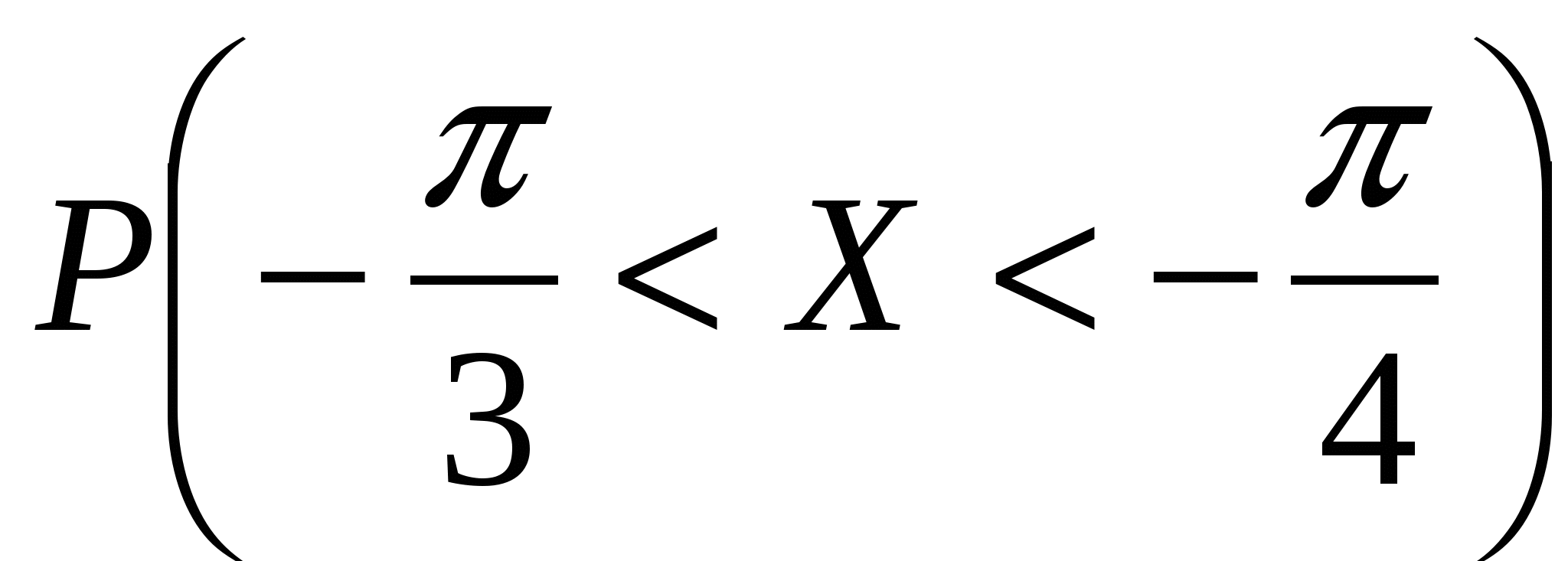
Построить графики функций распределения
| |
|
|
 Скачать 86.5 Kb.
Скачать 86.5 Kb.