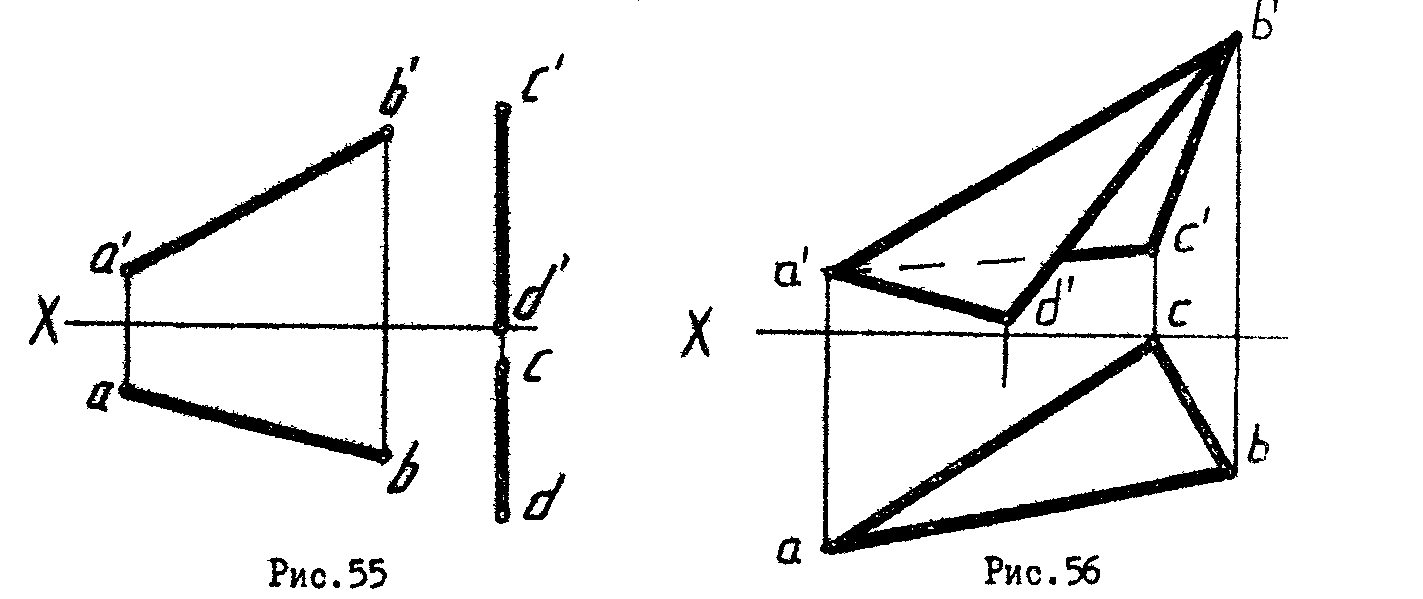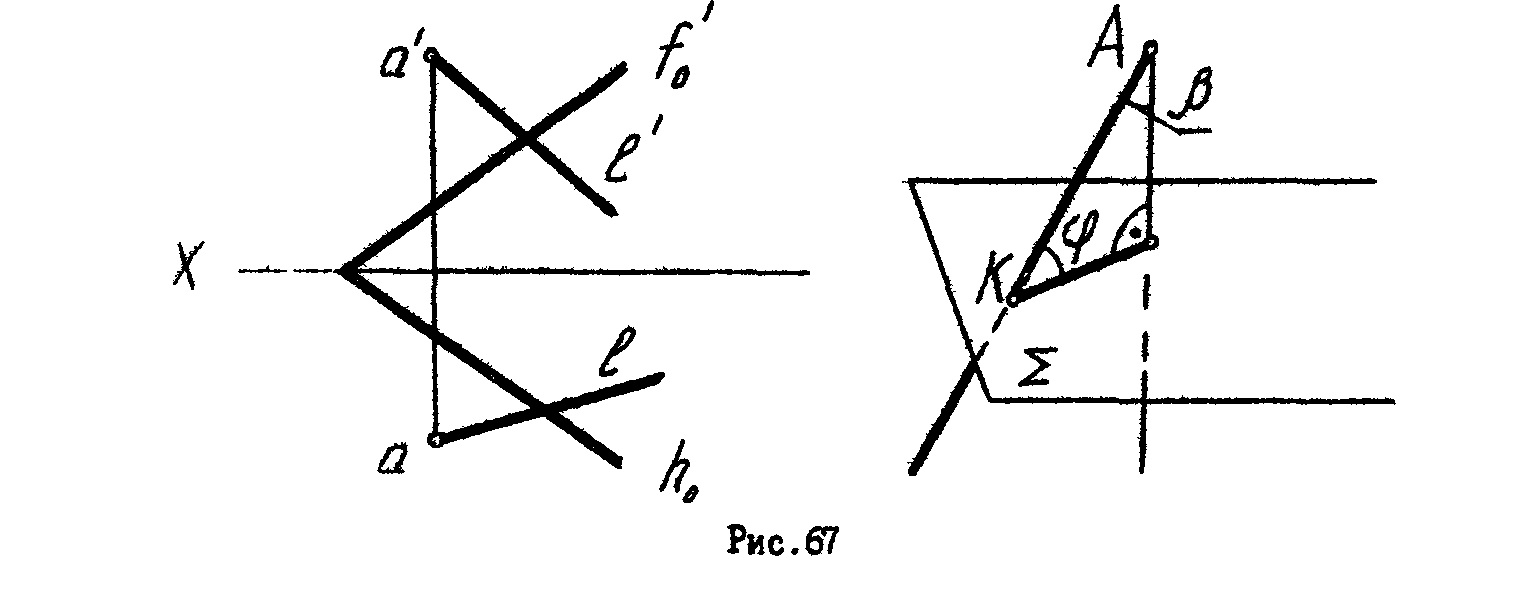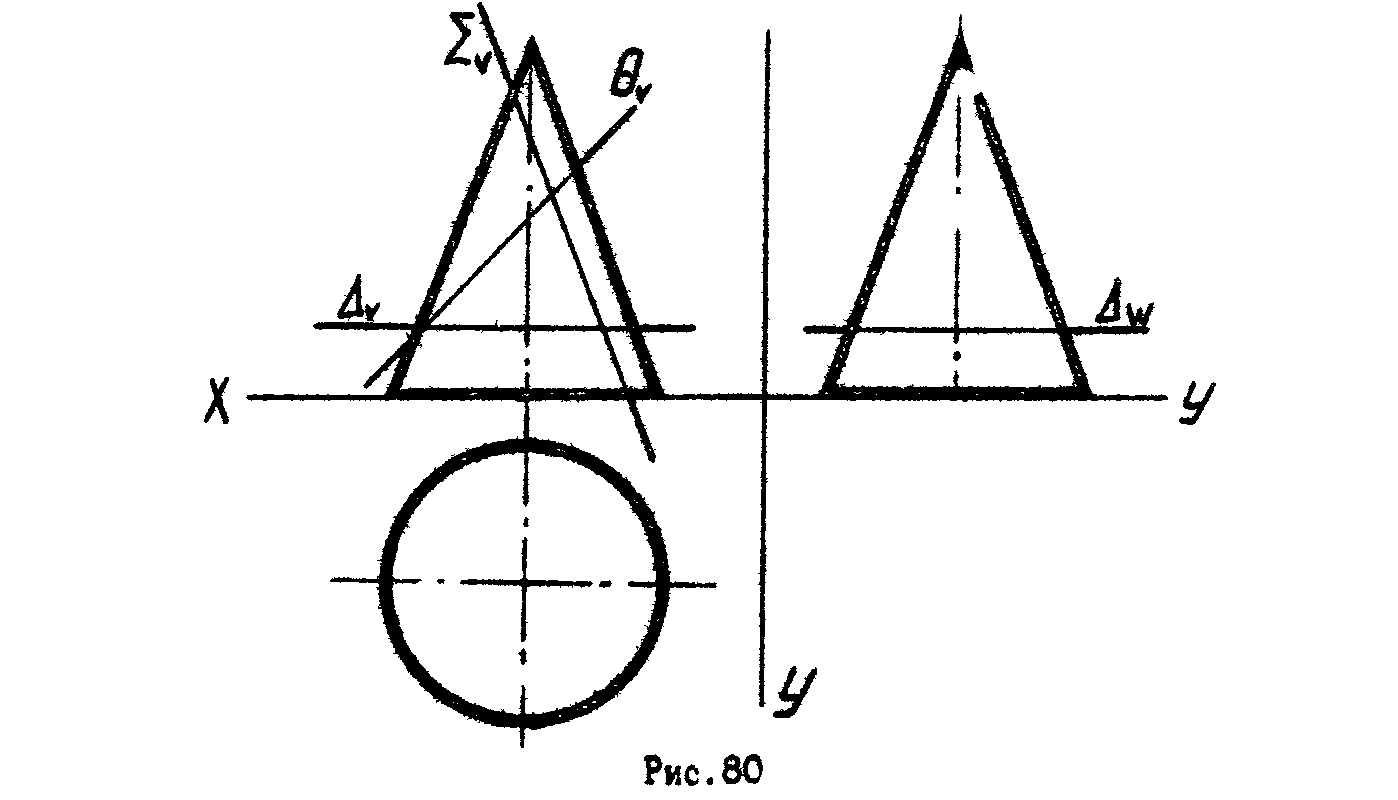|
|
методичка с домашними заданиями. Начертательная геометрия|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра технической механики
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Учебнометодическое пособие и упражнения
к практическим занятиям по инженерной графике
Уфа, 2011
В работе дано краткое описание теории по отдельным темам курса, приведены условия задач, указана литература.
Методические указания предназначены для бакалавров всех специальностей при изучении предметов «Начертательная геометрия» и «Инженерная графика».
Составители: Валитова Э.Г., старший преподаватель
Рецензент: Иванов С.П.; доцент, к.т.н.
Уфимский государственный нефтяной технический университет, 2011
Методические указания и упражнения предназначены для бакалавров всех специальностей при изучении предметов "Начертательная геометрия" и "Инженерная графика".
При работе с методическими указаниями бакалавр должен изучить материал по рекомендуемой литературе, которая указывается в каждой теме.
Цель проведения упражнений: закрепить знания теоретического материала, связать их с практическими примерами, освоить графические приемы решения задач, способствовать развитию пространственного представления.
Упражнения по курсу разбиты на 14 тем. К каждой теме дается краткое изложение теории, указывается литература, в также приводятся условия задач. Задачи, помеченные звездочкой, решаются дома, остальные в аудитории.
Бакалавр должен ознакомиться с темой занятия, прочитать указанную литературу.
Решение задач выполняется и тетради карандашом с применением чертежных инструментов и цветных карандашей (фломастеров или шариковых ручек с цветными пастами). Домашние задачи решаются в отдельной тетради.
В связи с тем, что бакалавру приходится решать задачи, относящиеся к пространственным предметам, необходимо все построения мысленно представлять в пространстве. Полезно прибегать к изготовлению простейших моделей (из бумаги, картона и т.п.), а также к выполнению пространственных чертежей.
В процессе изучения материала в соответствии с календарным планом бакалавр выполняет графические домашние работы (эпюры). Условия эпюрных задач и образцы их оформления приведены на стенде.
Консультации проводятся преподавателем еженедельно по кафедральному расписанию. На них проверяются и принимаются домашние работы бакалавров, проводится повторный программированный контроль знаний, даются пояснения по различным вопросам курса.
В конце семестра бакалавр должен сдать экзамен. К экзамену допускаются бакалавры, выполнившие и защитившие все расчетно графические работы.
Т Е М А 1
ТОЧКА И ЕЁ ПРОЕКЦИИ
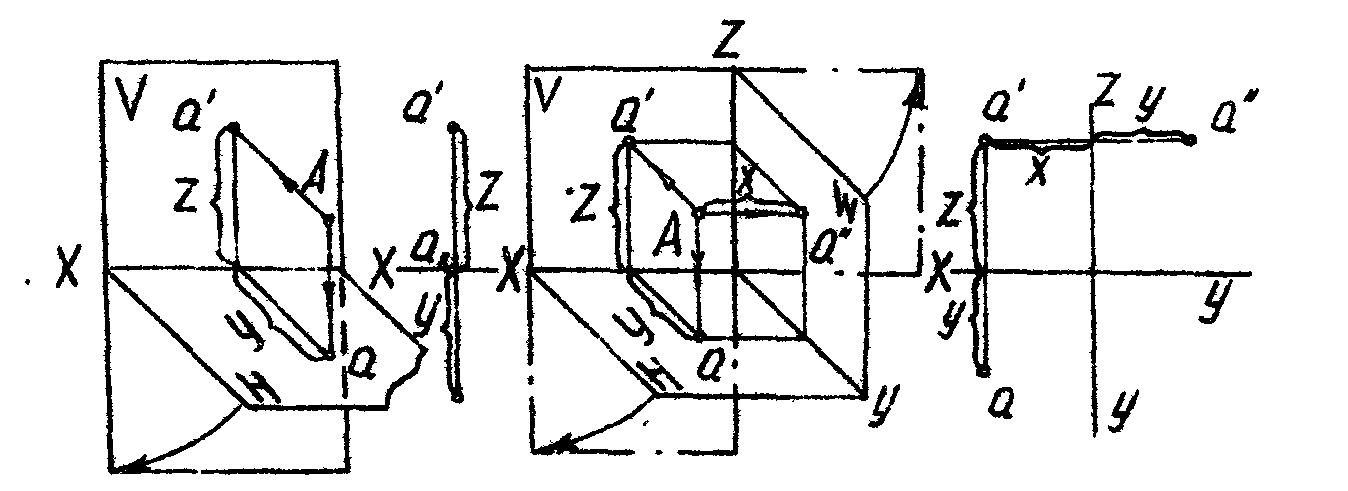
Точка в системе двух Точка в системе трех
плоскостей проекций плоскостей проекций
Положение точки в пространстве определяется ее координатами X,У, Z .т.е. расстоянием от точки до трех плоскостей проекций.
Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекций.
Эпюром (комплексный чертежом) называется плоский чертеж, полученный совмещением горизонтальной (Н) и профильной (W) плоскостей проекций с фронтальной (V) плоскостью проекций вращением H и W соответственно вокруг осей Х и Z. На эпюре фронтальная и горизонтальная проекции точки всегда располагаются на одной вертикальной линии связи
(а’a X). Фронтальная и профильная проекции всегда находятся на одной горизонтальной линии связи (а’a’’ Z)
Расстояние от фронтальной проекции точки до оси Xявляется высотой точки (расстоянием от точки до плоскости Н ), численное значение высоты определяется координатой Z.Аналогично, расстояние от горизонтальной проекции точки до оси X является глубиной точки (расстоянием от точки до плоскости V). Численное значение глубины определяется координатой У.
1. По наглядному изображению построить комплексный чертеж точек А, В, С (рис. 1).

2*. Построить изображения точек А (25,20,15) и В (20,25,0) на комплексном чертеже и на наглядном изображении по образцу точки С (35,10,30) (рис.2).

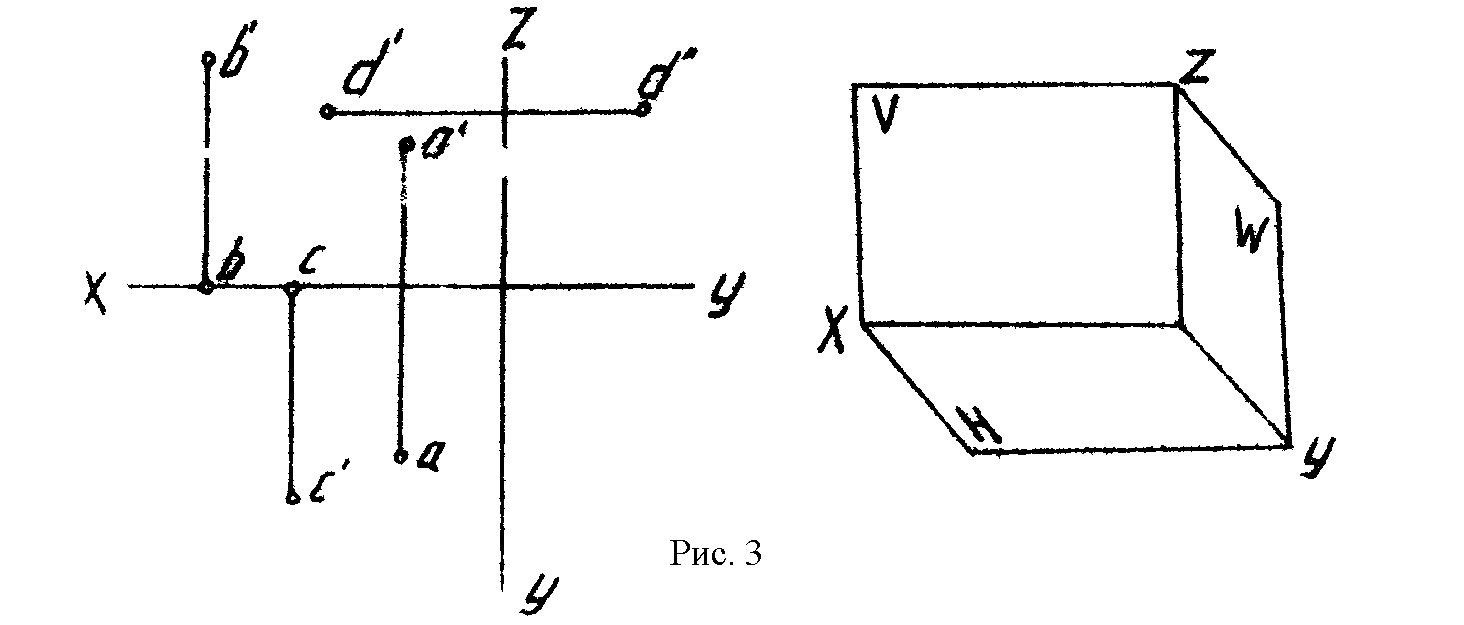
3*. По двум проекциям точек А, В, С, D построить третьи проекции и их наглядное изображение (рис. 3).
4.* Построить в трех проекциях точку В на расстоянии 30 мм от плоскости Н, 40 мм от плоскости V и 50 мм от плоскости W.
5. Даны три проекции точки А . Определить положение осей Х и У и расстояние от точки А в пространстве до плоскостей проекций (рис.4).
6. По фронтальной проекции точки А построить горизонтальную и профильную проекции так, чтобы ZА=2УА (рис.5).
7. Точка В симметрична точке А (-20, 25) относительно оси Х. Определить расположение точки В и записать ее координаты в системе 2-х плоскостей проекций.
8.* Заданы точки А, В, С. и D. Построить:
а) точку Е, расположенную над точкой А , взяв АЕ = 15мм;
б) точку F , расположенную под точкой В , взяв BF = 20 мм;
в) точку M , расположенную за точкой С, взяв СМ =10 мм;
г
) точку К , расположенную перед точкой D , взяв DК=5мм (рис. 6).
9. Дан параллелепипед с точкой А внутри. Построить:
а) точку В, симметричную точке А относительно верхней грани параллелепипеда;
б) точку С , симметричную точке А относительно передней грани;
в) точку D , симметричную точке А относительно правого верхнего ребра;
г) точку Е , симметричную точке А относительно верхнего переднего ребра;
д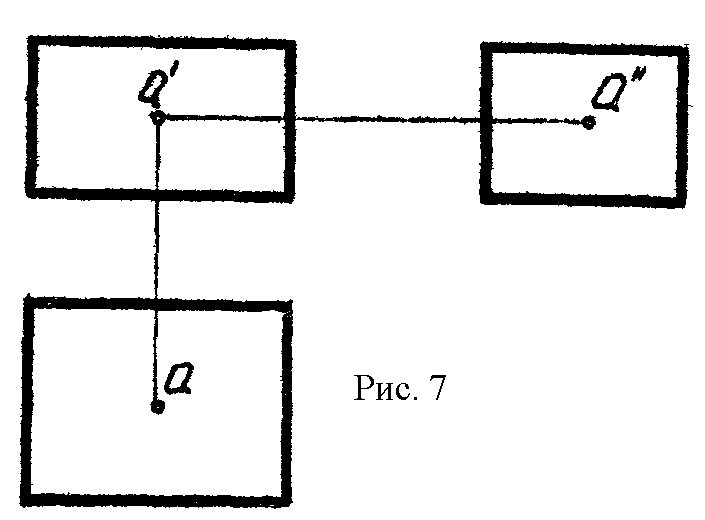
) точку F, симметричную точке А относительно нижней передней правой вершины (рис.7).
ТЕМА 2
П
РЯМАЯ, ЕЁ ПРОЕКЦИИ И СЛЕДЫ
Проекции Следы прямой Натуральная величина
прямой прямой
На эпюре прямая задается двумя ее проекциями. Проекциями прямой, в общем случае, являются прямые линии. Вырождение одной из проекций прямой в точку свойственно проецирующей прямой (перпендикулярной к соответствующей плоскости проекций).
Точка принадлежит прямой, если проекции точки принадлежат одновременно проекциям прямой (например, точка С на прямой АВ).
Точки пересечения прямой с плоскостями проекции называются следами прямой. Одна из координат следов равна нулю.
Натуральная величина отрезка прямой общего положения определяется величиной гипотенузы прямоугольного треугольника, построенного на одной из проекций как на катете. Второй катет треугольника равен разности расстояний концов отрезка от той плоскости проекций, на которой расположен первый катет.
1.* Построить комплексный чертеж и наглядное изображение прямой общего положения АВ в системе трех плоскостей А (38,10,38); В (5,42,5).
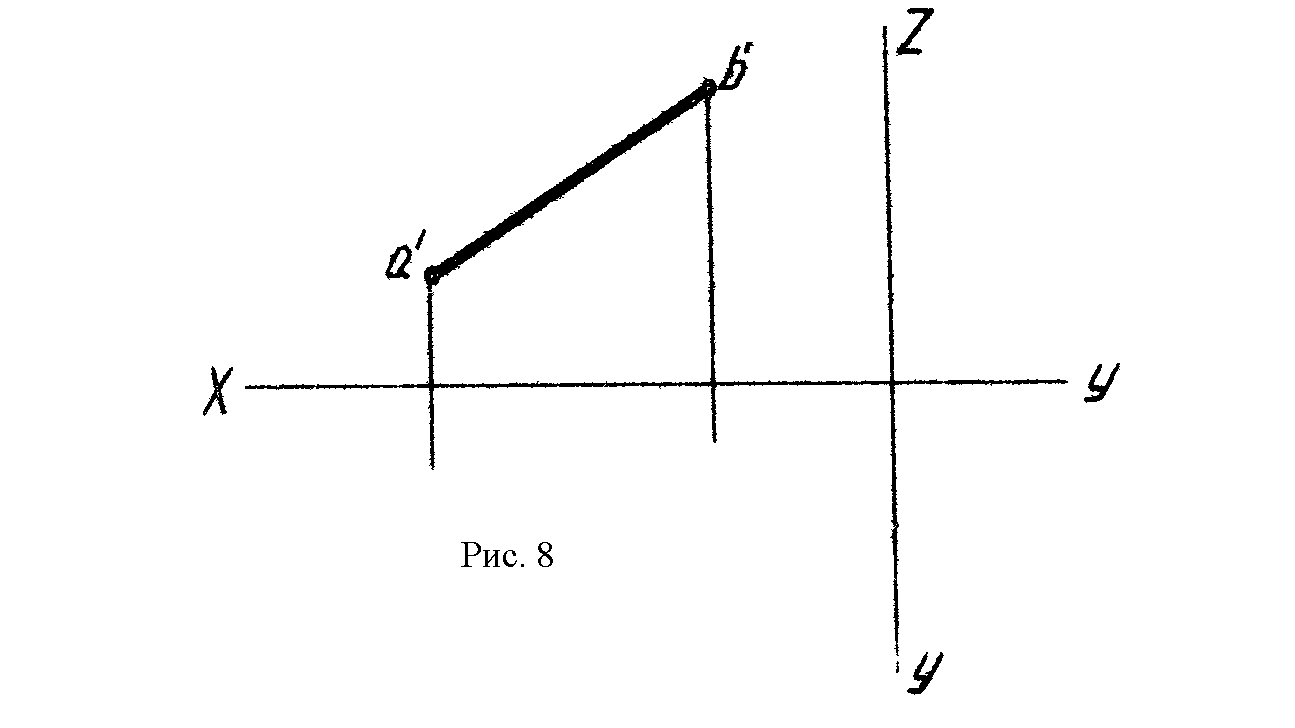
2. Фронталь АВ отстоит от плоскости V на 20мм. Построить две другие проекции прямой АВ. Определить натуральную величину отрезка АВ и углы наклона его к плоскостям проекций. На АВ найти точку М, делящую отрезок АВ в отношении АМ : МВ = 2:3 (рис. 8).
3. Определить натуральную величину отрезка АВ и углы наклона его к горизонтальной и фронтальной плоскостям проекций (рис. 9).

Рис. 9
4. Достроить фронтальную проекцию отрезка АВ, зная, что он наклонен в пространстве к горизонтальной плоскости проекций под углом 30° (рис .10).
5. Не прибегая к построению профильной проекции построить фронтальную проекцию точки К, принадлежащей прямой CD (рис.11).

6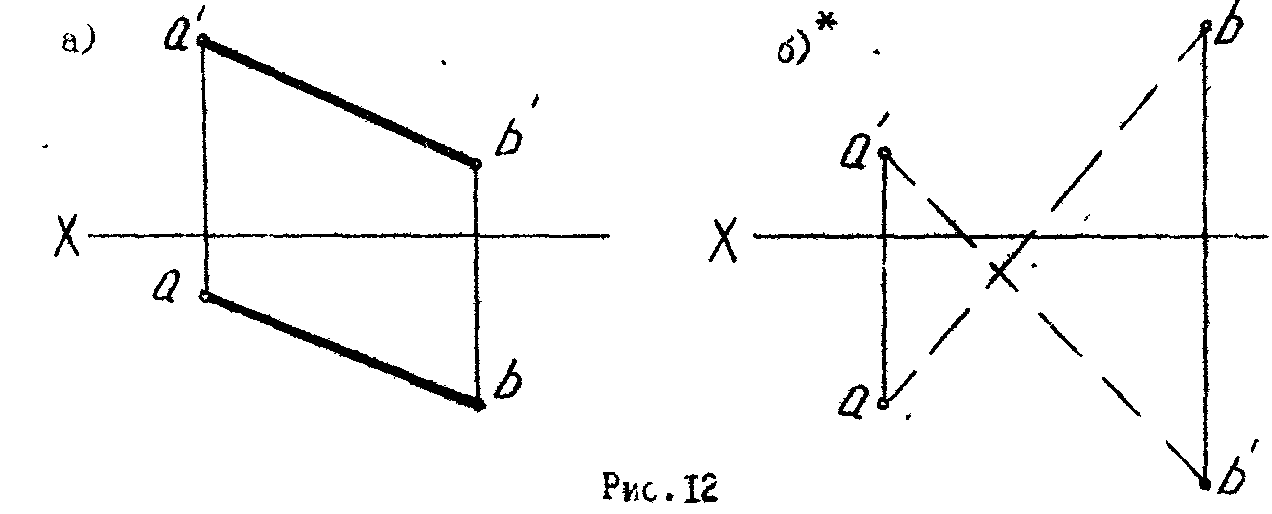
. Построить следы М и N прямой АB . Указать. через какие четверти прямая проходит, и отметить ее видимую часть (рис. 12).
7*. Определить натуральную величину расстояния между следами прямой и угол наклона ее к фронтальной плоскости проекций (рис. 13).

ТЕМА 3
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

Параллельные Пересекающиеся Скрещивающиеся
прямые прямые прямые
Одноименные проекции параллельных прямых в общем случае параллельны. Исключение составляют профильные прямые, для установления параллельности которых необходимо строить их профильные проекции.
Пересекающиеся прямые линии имеют одну общую точку, проекции которой находятся на одной линии связи.
Прямые, не пересекающиеся и не параллельные между собой, называются скрещивающимися. Проекции скрещивающихся прямых могут пересекаться, но точки их пересечения не лежат на одной линии связи. Точки М и N, лежащие на одном горизонтально - проецирующем луче, называются горизонтально конкурирующими; точки Р иQ, расположенные на одном фронтально проецирующем луче, называются фронтально конкурирующими. С помощью конкурирующих точек определяется видимость на комплексном чертеже.
1. Через точку К провести прямую параллельную прямой А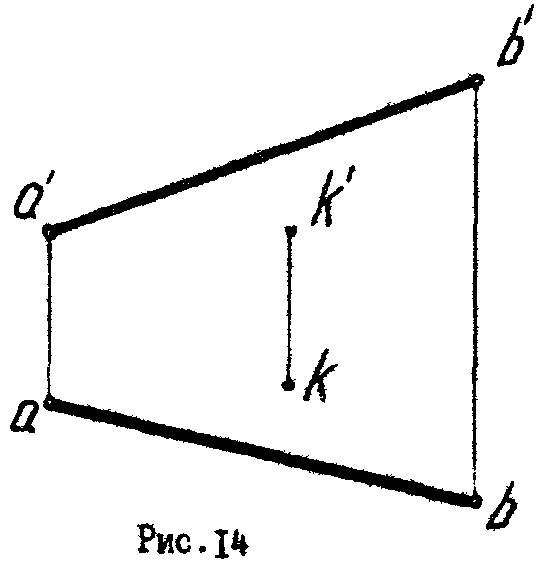
В(рис. 14).
2. Через точку А провести прямую, пересекающую данную прямую ВС в точке F, отстоящей от фронтальной плоскости проекций на 15 мм (рис.15).

Пересечь прямые АВ и СD прямой ЕК , проходящей через точку M (рис.16).

4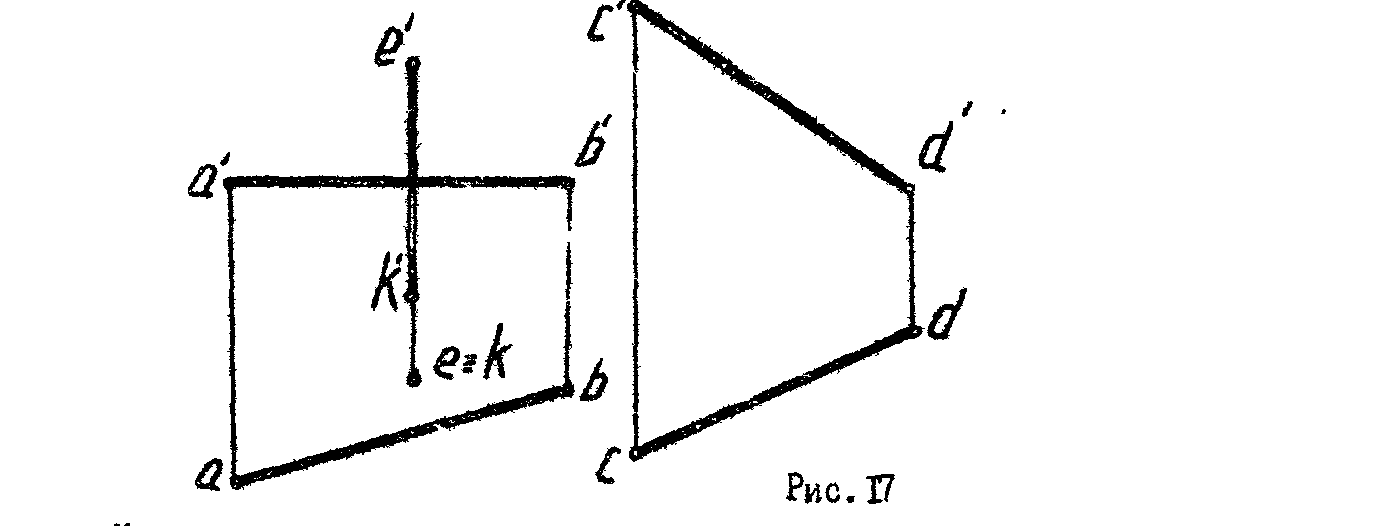
.* Пересечь прямые AB, CD, EK произвольной прямой МТ (рис.17).
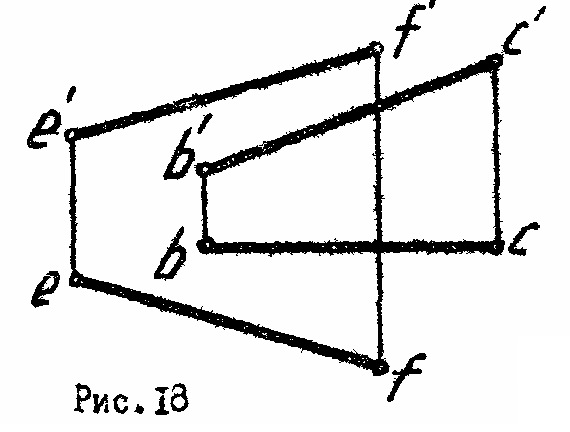
5.* Построить равнобедренный треугольник АВС с вершиной А на прямой EF (рис. 18).
6. Построить проекции квадрата ABCD по заданной стороне АВ и направлению горизонтальной проекции его смежной стороны m (рис. 19).
7
.* Определить видимость ребер треугольной пирамиды ABCD во всех проекциях (рис. 20).
ТЕМА 4
ПЛОСКОСТЬ. ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ
П
лоскость общего Главные линии
положения плоскости
Плоскость в пространстве и на эпюре может быть задана следующим образом: тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми; прямой и точкой, взятой вне прямой; плоской фигурой; следами. Каждый последующий вид задания может быть получен из предыдущего.
В зависимости от того, какое положение занимают плоскости относительно плоскостей проекций, их можно разделять на плоскости общего положения (не перпендикулярные и не параллельные плоскостям проекций) и плоскости частного положения. Последние могут быть проецирующими (перпендикулярными плоскостям проекций) и плоскостями уровня (параллельными плоскостям проекций). Плоскости частного положения задаются на эпюре одной линией - следом - проекцией.
Прямая линия принадлежит плоскости, если она имеет с ней две общие точки. Точка принадлежит плоскости, если эта точка лежит на прямой, принадлежащей плоскости.
К главным линиям плоскости общего положения относятся ее линии уровня (горизонталь, фронталь, профиль) и линии наибольшего наклона к каждой плоскости проекций. Линии наибольшего наклона служат для определения углов наклона плоскости к плоскостям проекций.
1. В данной плоскости построить недостающие проекции п
рямой l и точки М (рис.21).
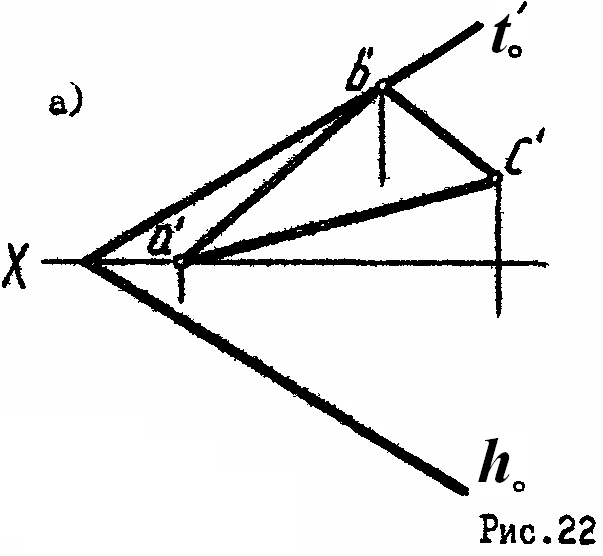
2. Построить недостающую проекцию треугольника АВС, расположенного в заданной плоскости (рис.22).
3. Построить недостающую проекцию плоской фигуры (рис.23).
4
. Построить фронтальный след плоскости , заданной горизонтальным следом и точкой А , в ней лежащей (рис.24).
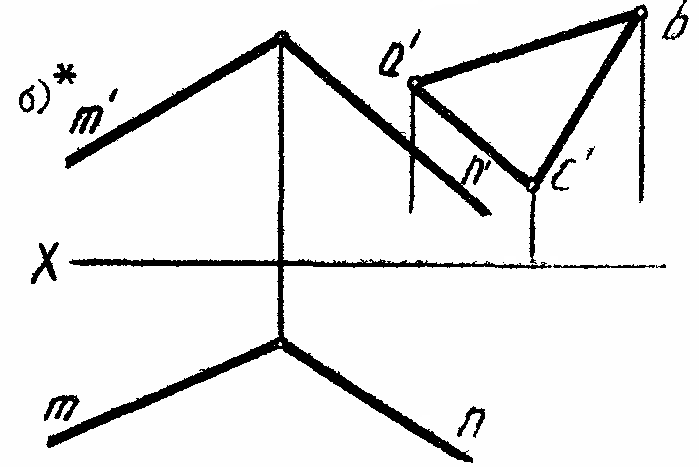
5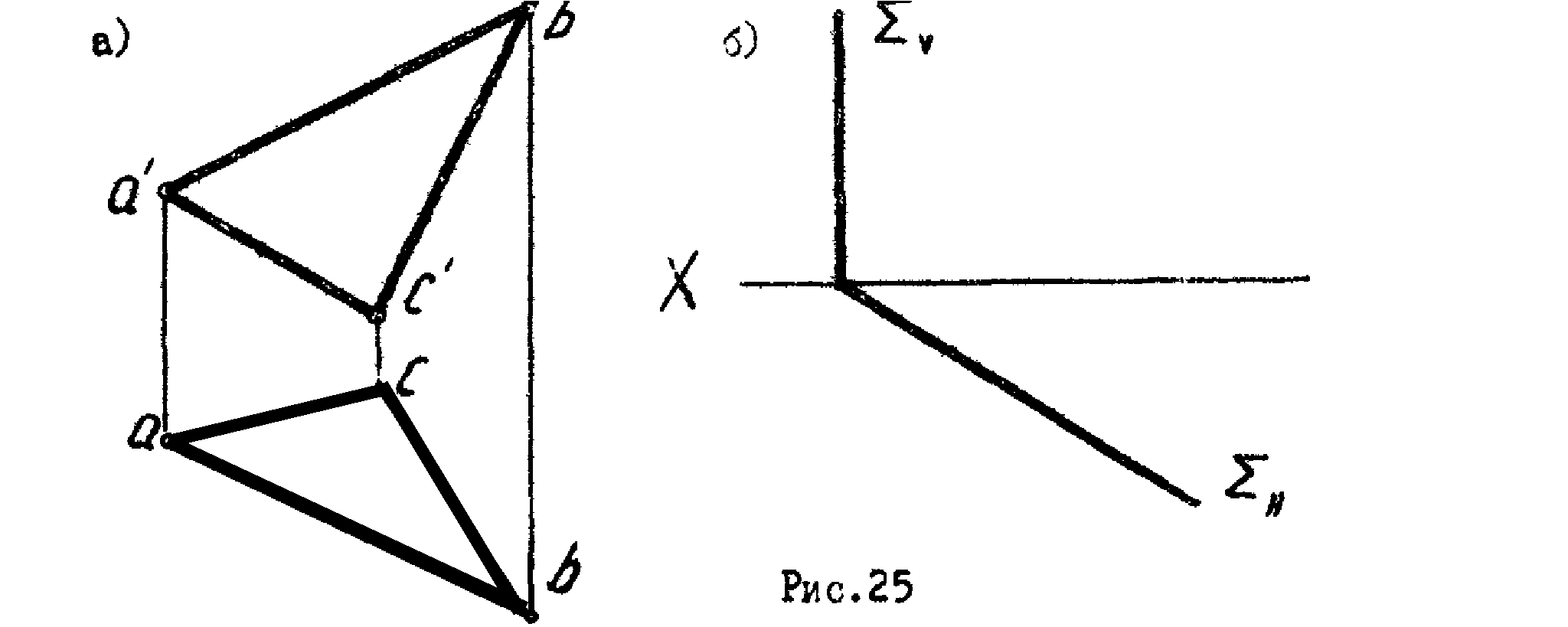
.* В данных плоскостях провести горизонтали и фронтали (рис.25).
6*. Построить горизонталь и фронталь плоскости, для которой отрезок АВ является линией ската (рис.26).
7
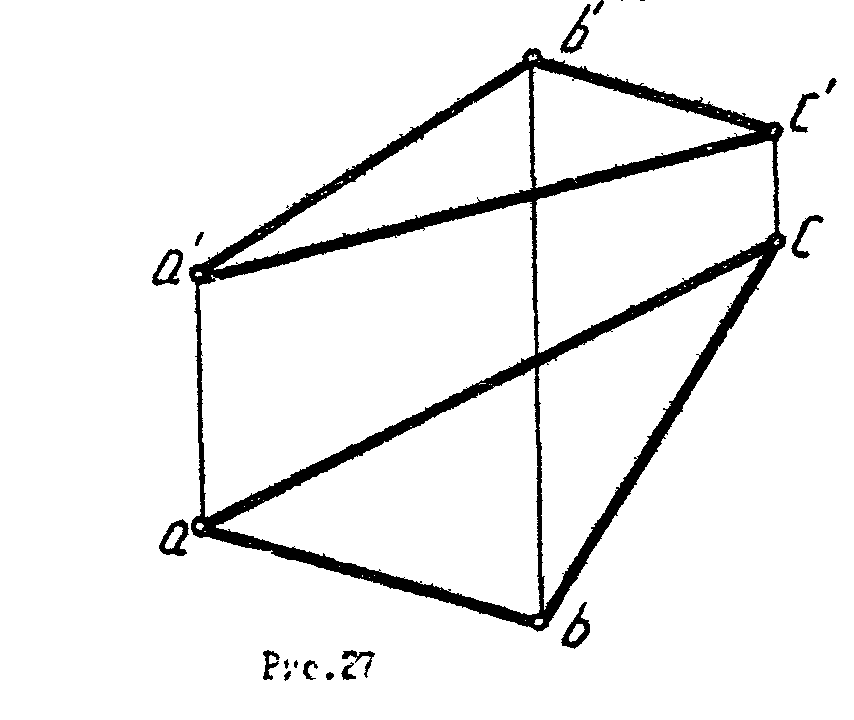
. В заданной плоскости провести линии наибольшего наклона и определить углы наклона ее к фронтальной и горизонтальной плоскости (рис.27).
Т Е М А 5
ВЗАИМНОЕ ПОЛ0ЖЕНИЕ ДКУХ ПЛОСКОСТЕЙ.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
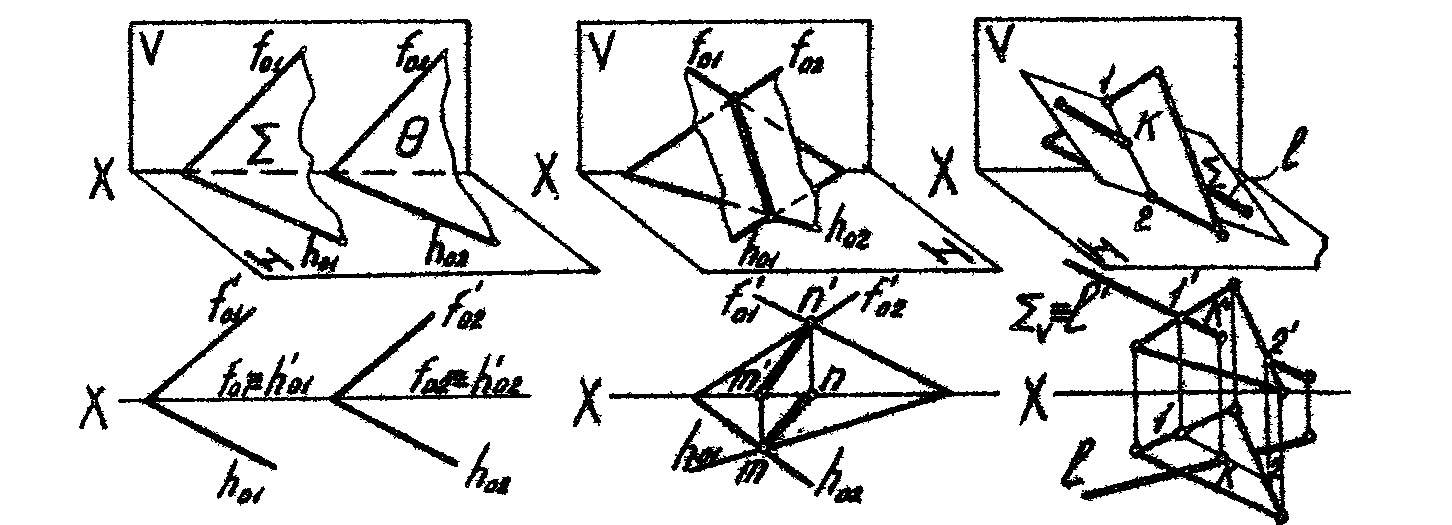
Параллельные Пересекающиеся Пересечение прямой
плоскости плоскости с плоскостью
Две плоскости могут быть параллельными или пересекаться. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Признаком параллельности плоскостей частного положения является взаимная параллельность их одноименных следов-проекций.
У пересекающихся плоскостей линия их пересечения определяются двумя точками, одновременно принадлежащими обеим плоскостям, либо одной общей точкой и известным направлением этой линии. Общие точки находятся способом вспомогательных плоскостей-посредников.
Точка пересечения прямой с плоскостью (точка встречи) определяется как точка, принадлежащая одновременно и прямой и плоскости. Находят ее в такой последовательности: 1) прямую заключают в проецирующую плоскость; 2) строят линию пересечения вспомогательной и заданной плоскости; 3) находят точку встречи на пересечении полученной линии с заданной прямой.
Прямая параллельна плоскости, если она параллельна какой-либо прямой этой плоскости.
1.* Построить следы плоскости, проходящей через точку А, пар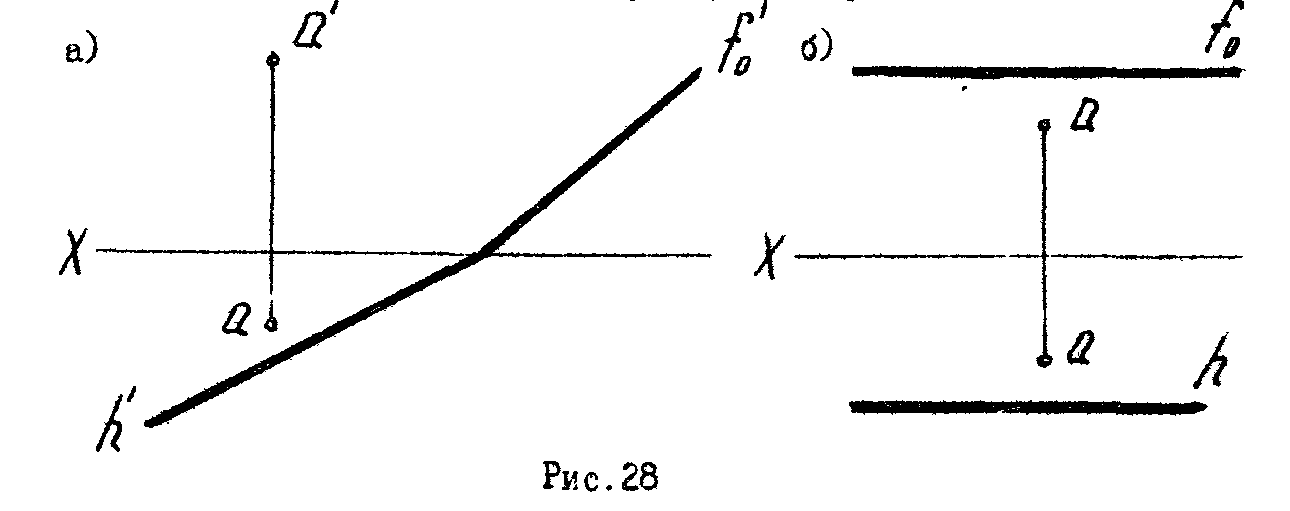
аллельно заданной плоскости в примерах на рис. 28.
2. Построить горизонтальную проекцию треугольника АВС так, чтобы его плоскость была параллельна заданной плоскости.
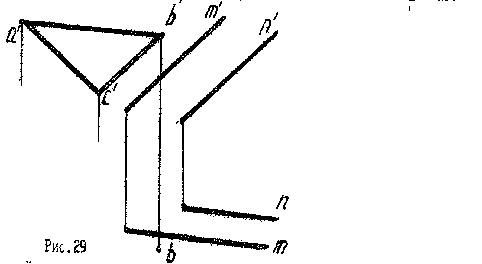
3.* Через точку А провести плоскость , параллельную данной прямой l- и перпендикулярную к горизонтальной плоскости проекции (рис .30).
Р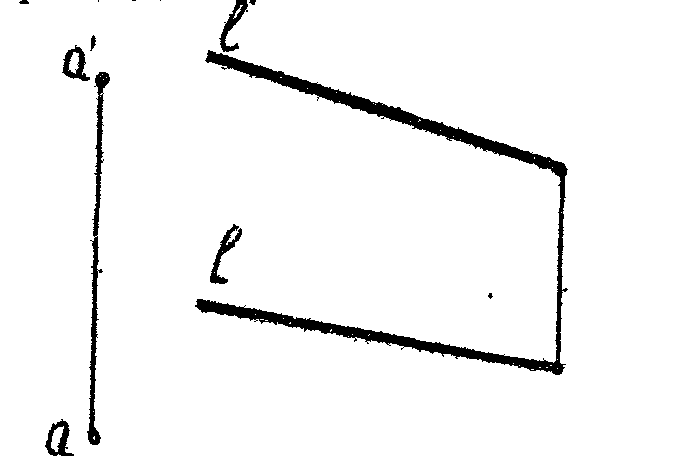
ис. 30
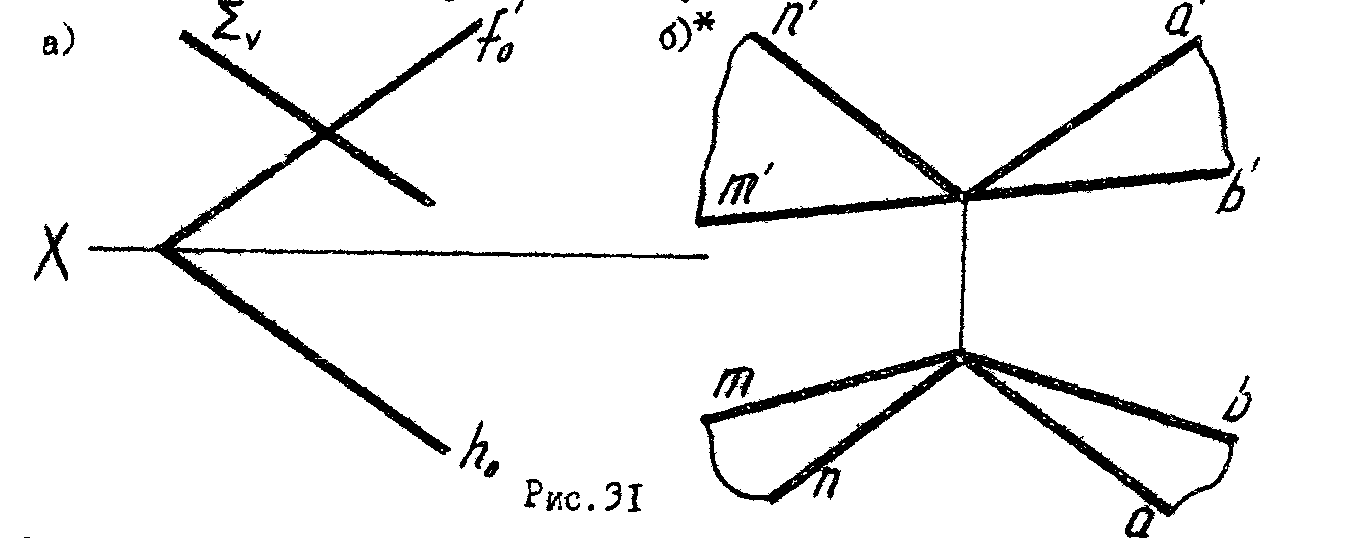
4. Построить линии пересечения двух плоскостей (рис. 31).
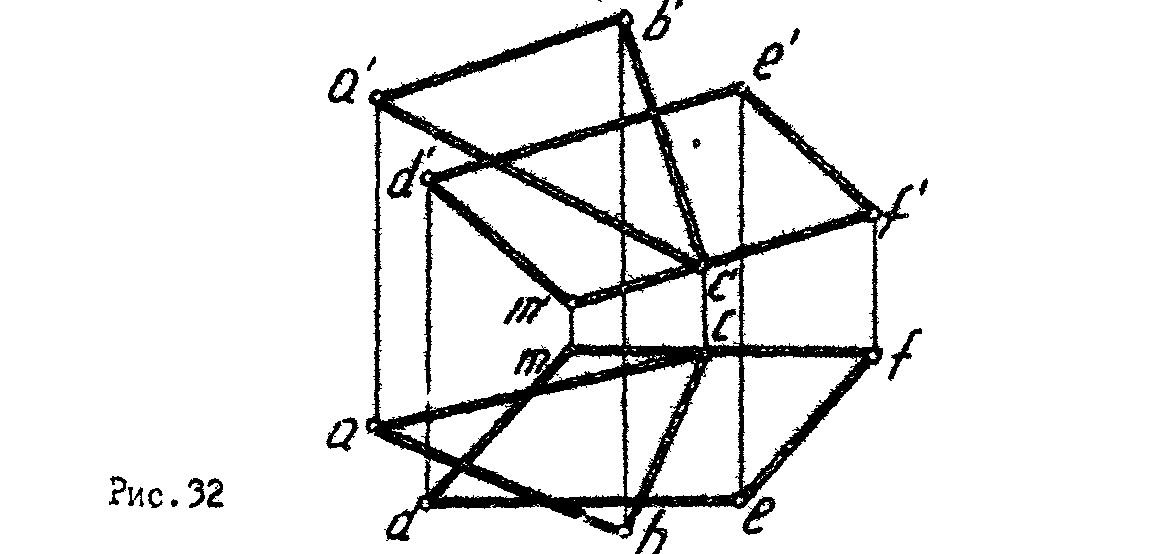
5. Построить линию пересечения двух плоских фигур, одна из которых задана треугольником АВС, а вторая – четырехугольником DEFM. Определить видимость (рис. 32).
6. Построить точку пересечения прямой с плоскостью (рис. 33).

7.* Провести через точку К прямую, пересекающую заданные прямые АВ и CD (рис.34).
8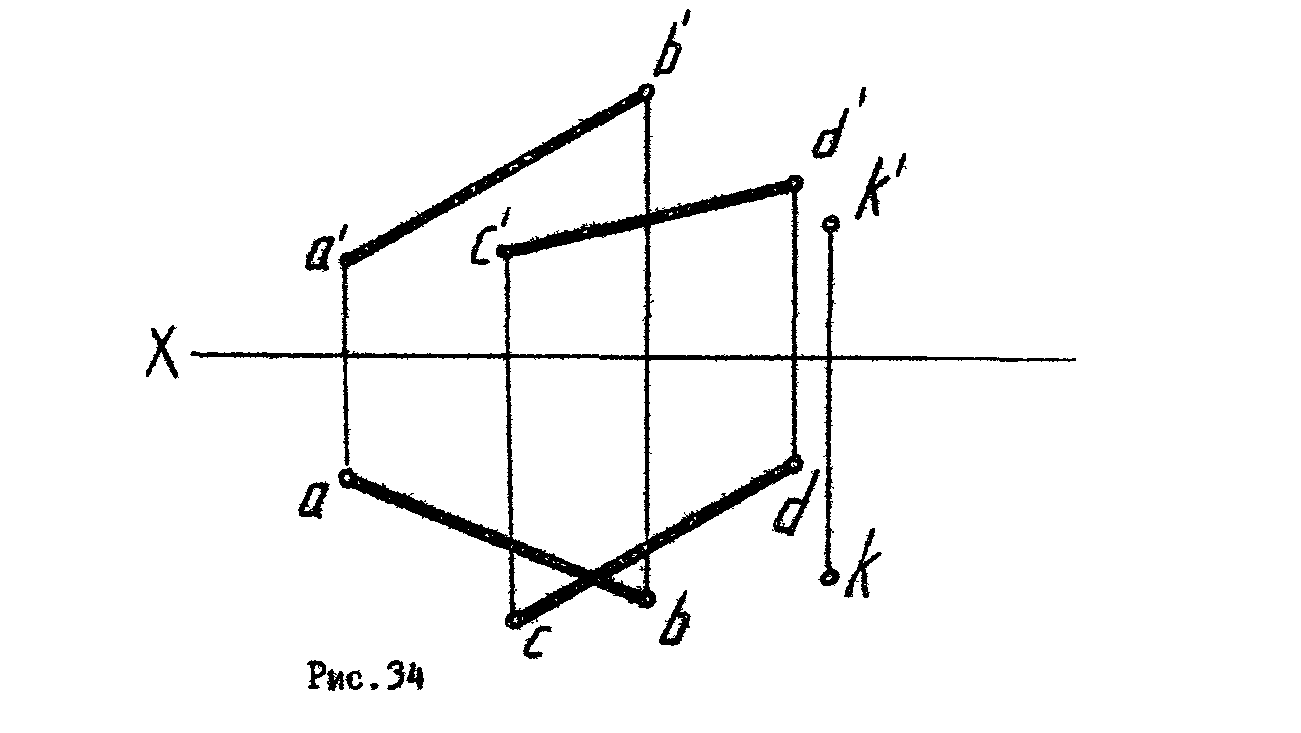
. Через точку А провести прямую, параллельную заданной плоскости (m || n) и пересекающую прямую l(рис. 35).
9. Провести прямую m, параллельную прямой l и пересекающую прямые а и b (риc. 36).

Т Е М А 6
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ,
ДВУХ ПЛОСКОСТЕЙ
П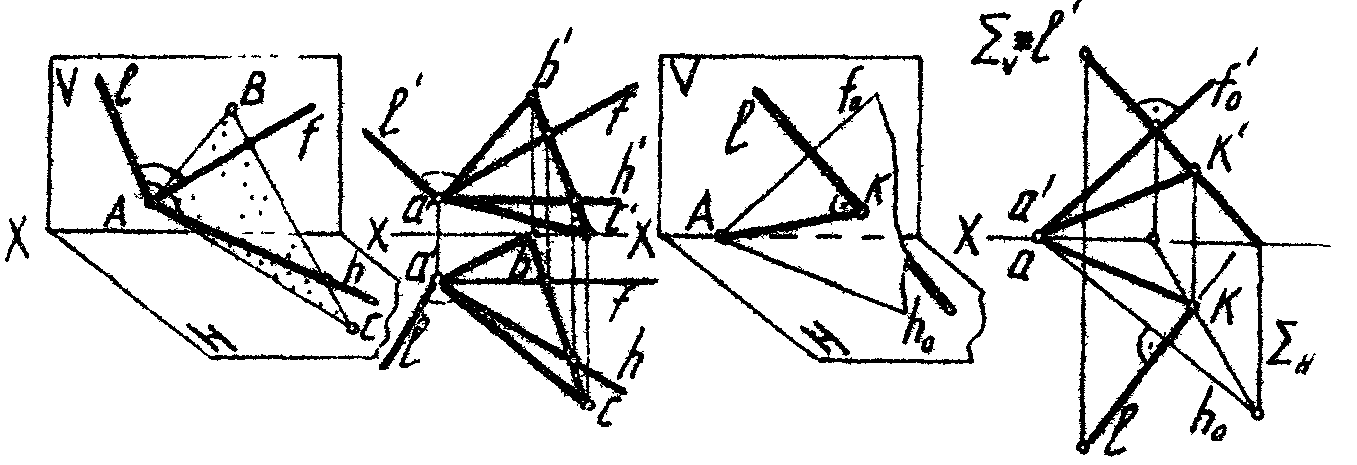
рямая, перпендикулярная Взаимно-перпендикулярные
плоскости прямые общего положения
В основу определения перпендикулярности прямых и плоскостей на эпюре положена теорема о проецировании прямого угла, если одна из сторон прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то на эту носкость прямой угол проецируется без искажения.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На плоскости общего положения такими прямыми выбираются линии уровня - горизонталь и фронталь. Тогда проекции перпендикуляра l к плоскости будут перпендикулярны соответствующим проекциям линий уровня ( lh, l’f’)
Две плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Две прямые взаимно перпендикулярны, если одна из них лежит в плоскости, перпендикулярной второй прямой. Взаимно перпендикулярные прямые могут пересекаться или быть скрещивающимися.
1. Найти проекцию и натуральную величину перпендикуляра, опущенного из точки D на заданную плоскость (рис 37).
2. Из точки А опустить перпендикуляр на прямую ВС и определить его натуральную величину (рис. 38).

3.* Через прямую АВ провести плоскость, перпендикулярную к заданной плоскости (рис.39).

4.* Построить сферу радиусом 40 мм , касательную к плоскости
(m n) в точке К (рис.40).
5.* Найти точку В, симметричную точке А относительно заданной плоскости (рис.41).
6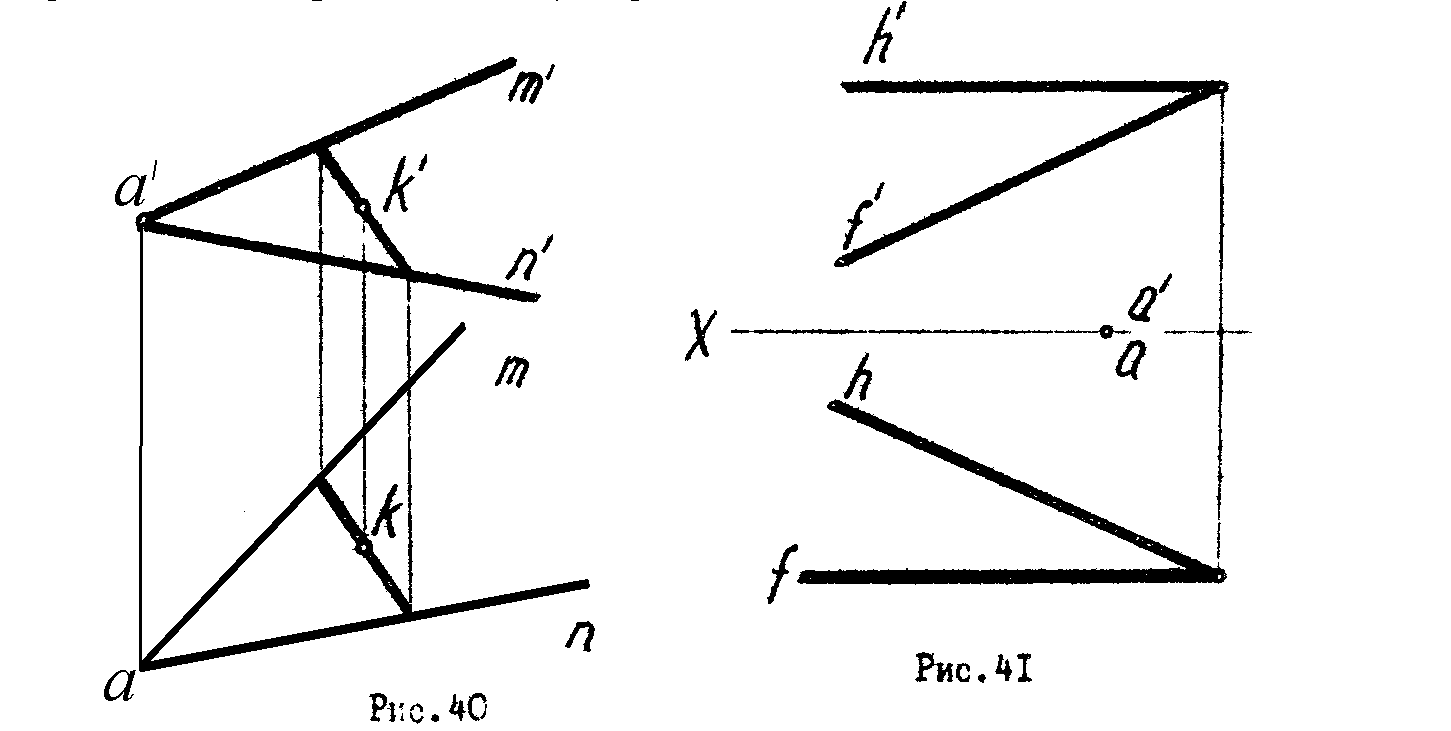
. Найти точку D , симметричную точке С относительно данной прямой (рис.42).
7. Построить горизонтальную проекцию прямой b , пересекающей заданную прямую а под прямым углом (рис. 43).

ТЕМА 7
ГЕОМЕТРИЧЕСКИЕ МЕСТА
1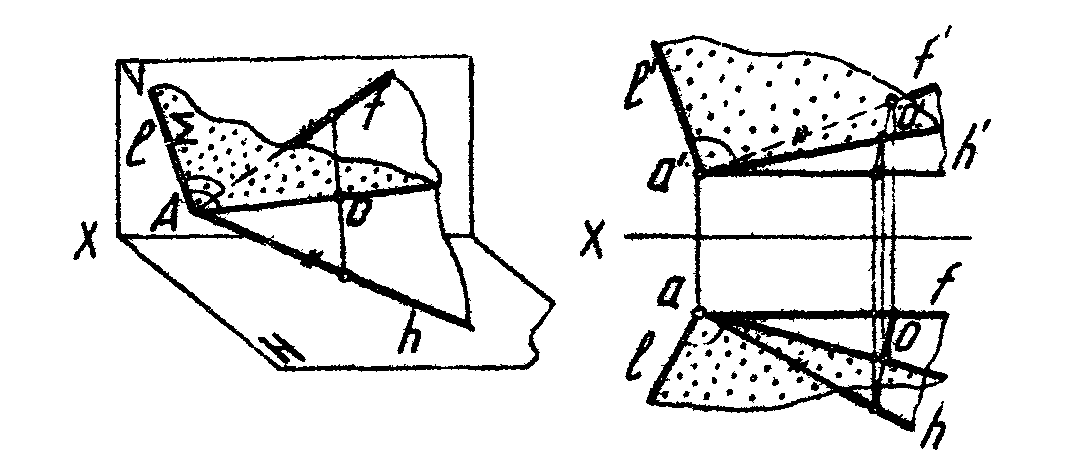
. Геометрическим местом точек (г.м.т.) пространства, равноудаленных от двух заданных точек, является плоскость, проходящая через середину отрезка между точками и перпендикулярная к нему.
2. Г.м.т. равноудаленных от четырех точек пространства, является центр шара с этими точками на его поверхности.
3. Г.м.т. пространства, равноудаленных от 3 параллельных прямых, не лежащих в одной плоскости есть ось цилиндра, образующими которого являются заданные прямые.
4. Г.м.т. пространства, равноудаленных от 3 пересекающихся плоскостей, является линия центров шаров, касательных к заданным плоскостям (линия пересечения 2-х биссекторных плоскостей).
5. Геометрическим местом прямых (г.м.п.) пространства, проходящих через точку под заданным углом к плоскости, является совокупность образующих кругового конуса, наклоненных под заданным углом к плоскости с вершиной в заданной точке.
6. Г.м.п. пространства, параллельных заданной прямой и удаленных от нее на заданное расстояние, является совокупность образующих кругового цилиндра, ось которого есть данная прямая, а радиус - заданное расстояние.
7. Г.м т., удаленных от данной плоскости на заданное расстояние является пара параллельных ей плоскостей, отстоящих от данной плоскости на заданное расстояние.
8 Г.м.т., равноудаленных от двух пересекающихся прямых, является плоскость, проходящая через биссектрису угла между заданными прямыми и перпендикулярная к плоскости этих прямых.
1. Построить геометрическое место точек пространства, отстоящих от плоскости (АВС) на 20 мм.
2*. На прямой l найти точку, равноудаленную от фронтальной и горизонтальной плоскостей проекций, не прибегая к построению профильной проекции прямой (рис.45).
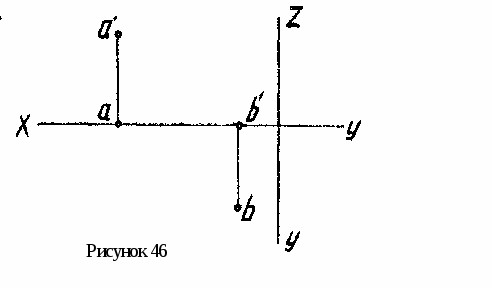
3. На оси 0Z найти точку С , равноудаленную от точек А и B (рис. 46).
4. Построить прямую l, параллельную плоскости () и касающ
уюся в точке К шара с центром в точке С (рис.47).
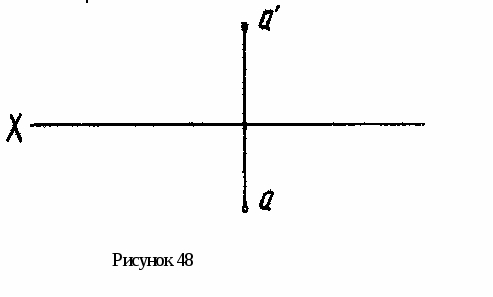
5*. Через точку А провести прямую, образующую с горизонтальной плоскостью проекций угол 45,с фронтальной - угол 30°
6*. Через точку А провести прямую, наклоненную к горизонтальной плоскости проекций под углом 40° и параллельную плоскости (h).

ТЕМА 8
СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
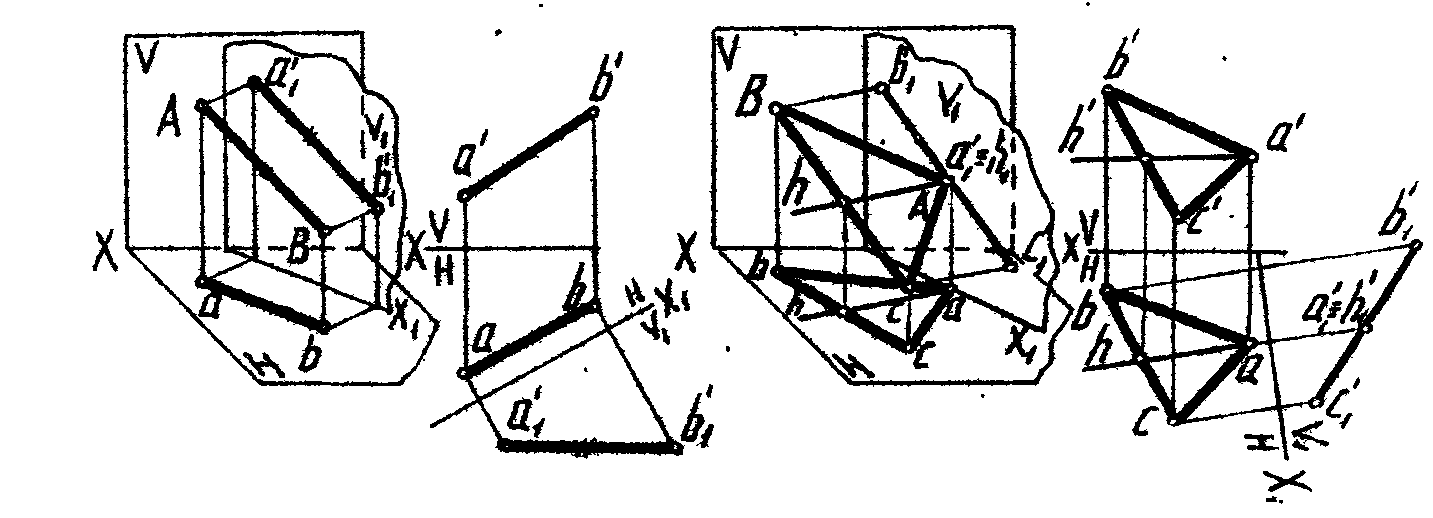
В этом способе преобразования рассматриваемый объект, оставаясь неподвижным в пространстве, занимает частное положение относительно новой плоскости проекций, взаимная перпендикулярность плоскостей проекций сохраняется. При замене фронтальной плоскости проекций остается неизменной координата Z , при замене горизонтальной плоскости - координата У.
Заменой плоскостей проекций можно придать заданным геометрическим элементам частное положение и этим упростить решения многих задач.
Заменой одной плоскости проекций можно:
1) прямую общего положения преобразовать в линию уровня, если новую плоскость проекций выбрать параллельно прямой;
2) линию уровня преобразовать в проецирующую прямую, если новую плоскость проекций ввести перпендикулярно к прямой;
3) плоскость общего положения преобразовать в проецирующую, если новую плоскость проекций выбрать перпендикулярной к линии уровня заданной плоскости;
4) проецирующую плоскость преобразовать в плоскость уровня, если новую плоскость проекций провести параллельно заданной плоскости;
5) прямую общего положения преобразовать в проецирующую (выполняются последовательно пункты 1 и 2);
6) плоскость общего положения преобразовать в плоскость уровня, выполнив последовательно пункты 3 и 4.
1. Определить натуральную величину отрезка АВ и углы наклона его к горизонтальной и фронтальной плоскостям проекций (рис.50).
2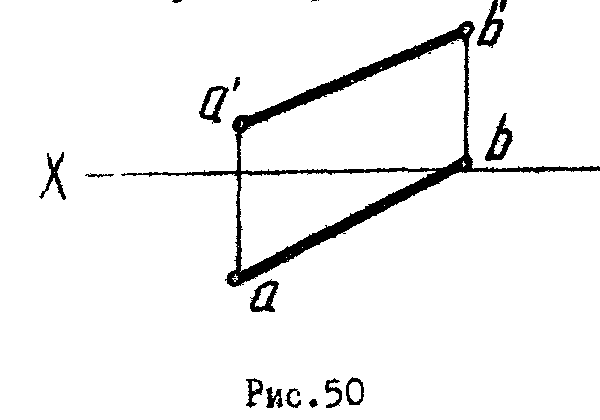
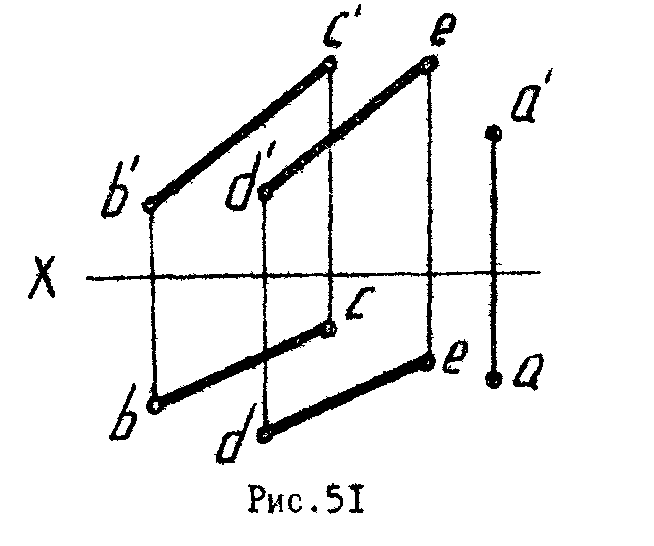

. Определить расстояние от точки А до плоскости и построить проекции перпендикуляра (рис.51).
3.* Определить расстояние между параллельными плоскостями Q (f, h) и P (to, ho) и угол наклона их к горизонтальной плоскости проекций (рис.52).
4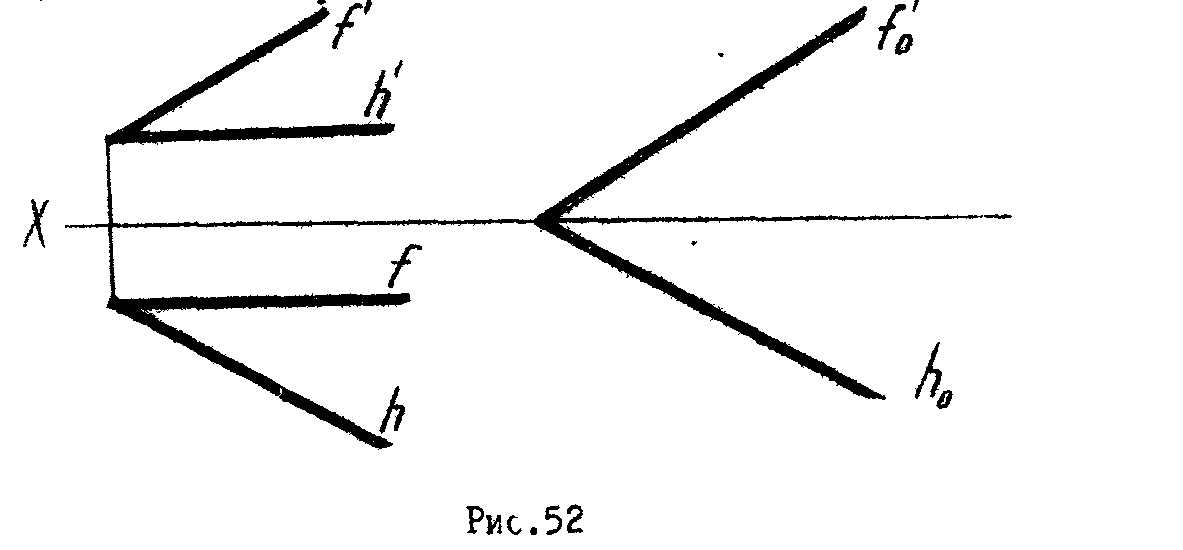
. Определить натуральную величину треугольника АВС (рис.53)
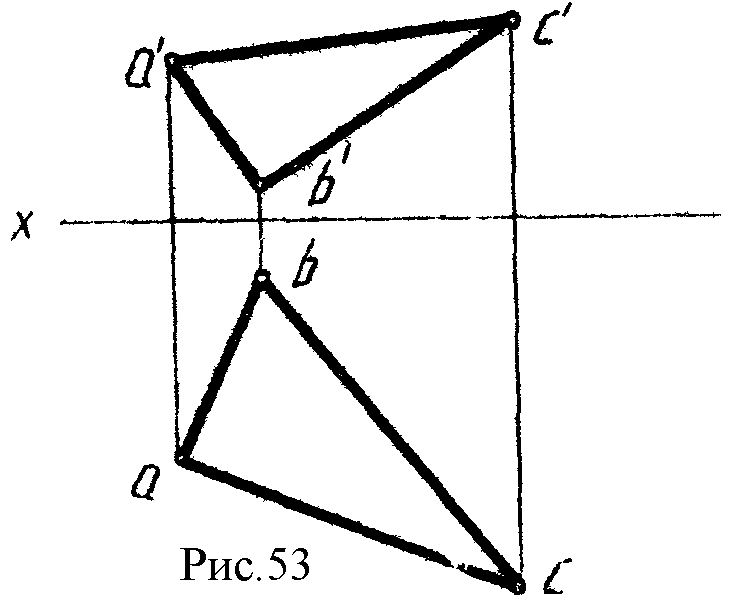
5.* Определить величину двугранного угла при ребре АВ (рис.54).

6. Определить расстояние между прямыми АВ и СD и найти проекции ближайших точек (рис. 55).
7.* Построить проекции А, В, D треугольника ABD, зная, что двугранный угол при ребре АВ = 30° (рис.56).
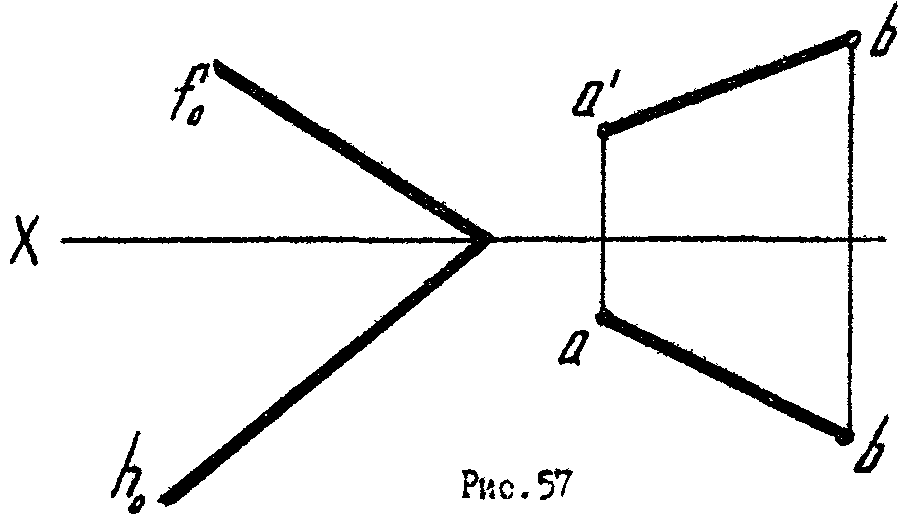
8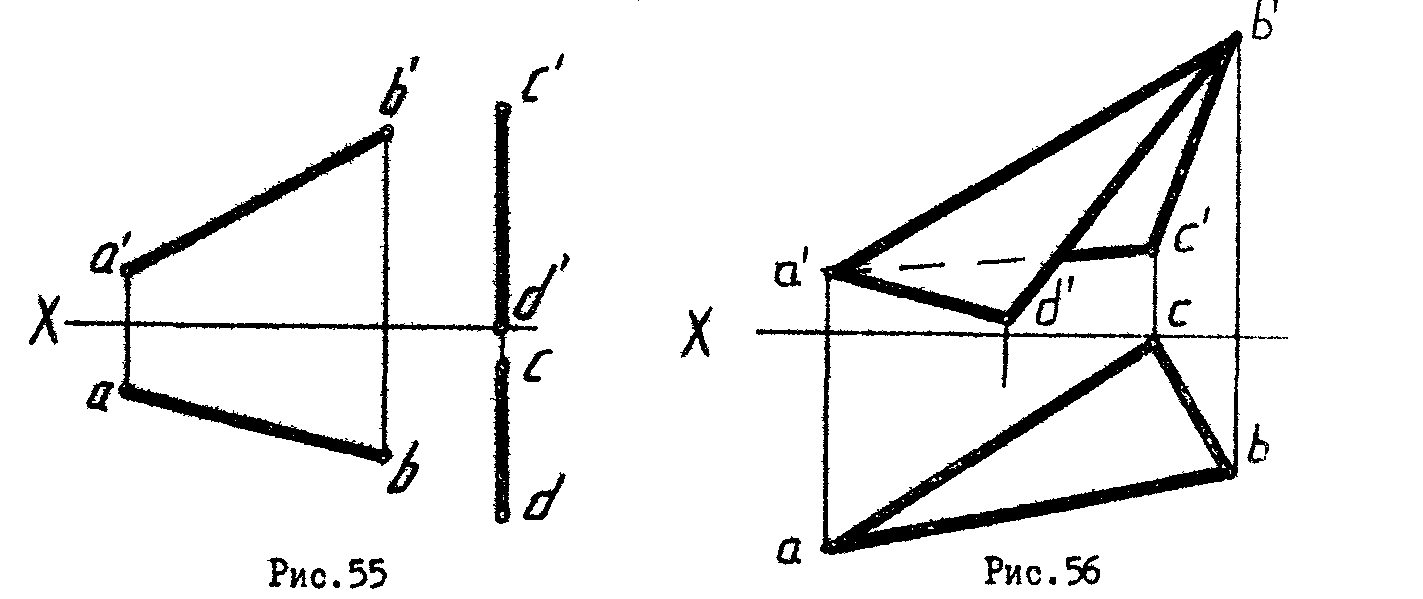
.* На прямой АВ найти точку К, отстоящую от плоскости ( f h) на расстоянии 20мм (рис.57).
ТЕМА 9
СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ОСИ.
ПЛОСКОПАРАЛЛЕЛЬНОЕ ПЕРЕМЕЩЕНИЕ
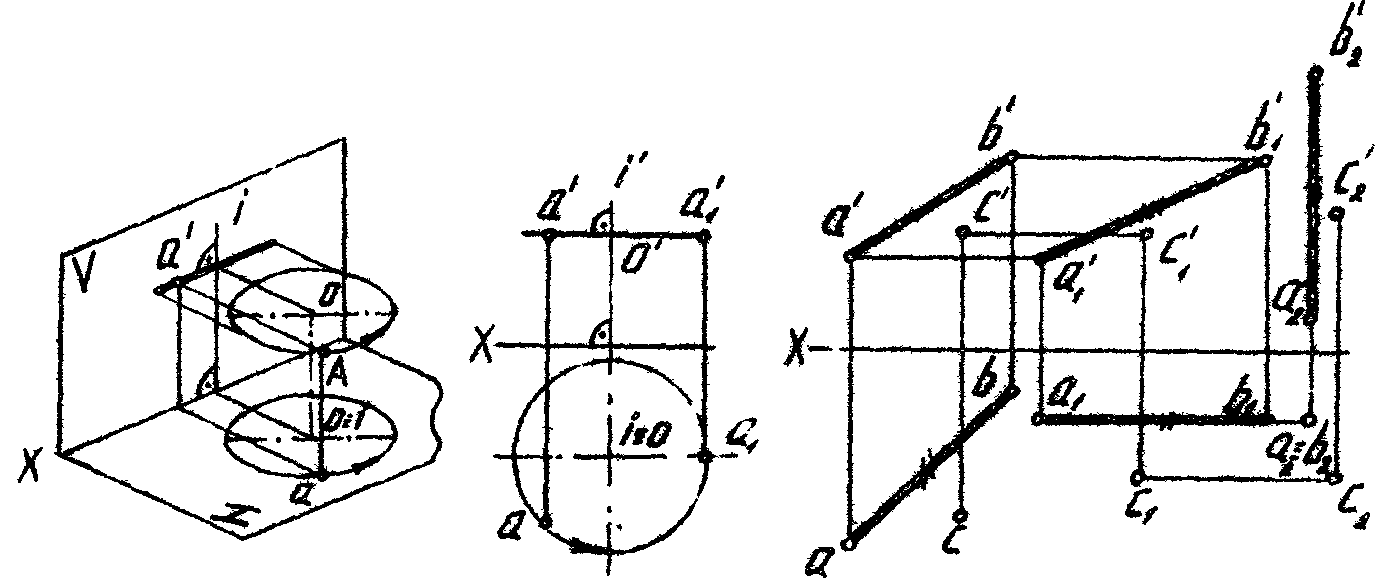
Вращение вокруг оси, перпендикулярной Плоско - параллельное
плоскости проекций перемещение
При вращении точки вокруг оси, перпендикулярной плоскости проекций, одна ее проекция перемещается по окружности, а вторая по прямой перпендикулярной проекции оси вращения. Плоско- параллельное перемещение рассматривается как вращение вокруг проецирующей оси без указания оси вращения.
Одним плоско - параллельным перемещением можно достичь тех же результатов, что и одной заменой плоскостей проекций, а именно: определить натуральную величину отрезка прямой общего положения и углы наклона его к плоскостям проекций (одним преобразованием -один угол); определить расстояние между двумя точками, двумя параллельными плоскостями общего положения (преобразовав их в проецирующие); определить натуральную величину плоской фигуры, лежащей в проецирующей плоскости и т.п.
Двумя плоско - параллельными перемещениями определяются: расстояние от точки до прямой общего положения, расстояние между двумя прямыми общего положения, натуральная величина плоской фигуры, лежащей в плоскости общего положения, размер плоского угла, двугранного угла при ребре общего положения и др.
1*. Вращением определить натуральную величину отрезка АВ и углы наклона его к фронтальной и горизонтальной плоскостям проекций (рис.58).
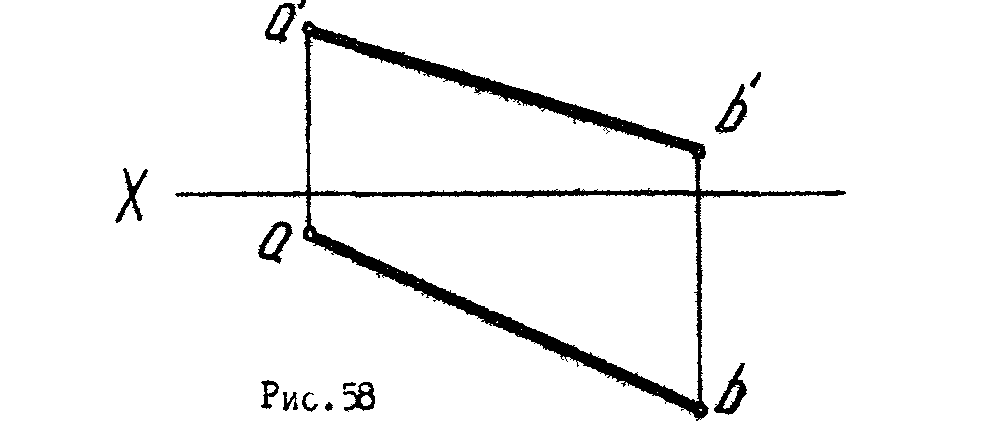
2. Вращением определить углы наклона заданной плоскости к горизонтальной и фронтальной плоскостям проекций (рис.59).

3. Точку К повернуть вокруг оси 0 до совпадения с плоскостью треугольника АВС (рис. 60).
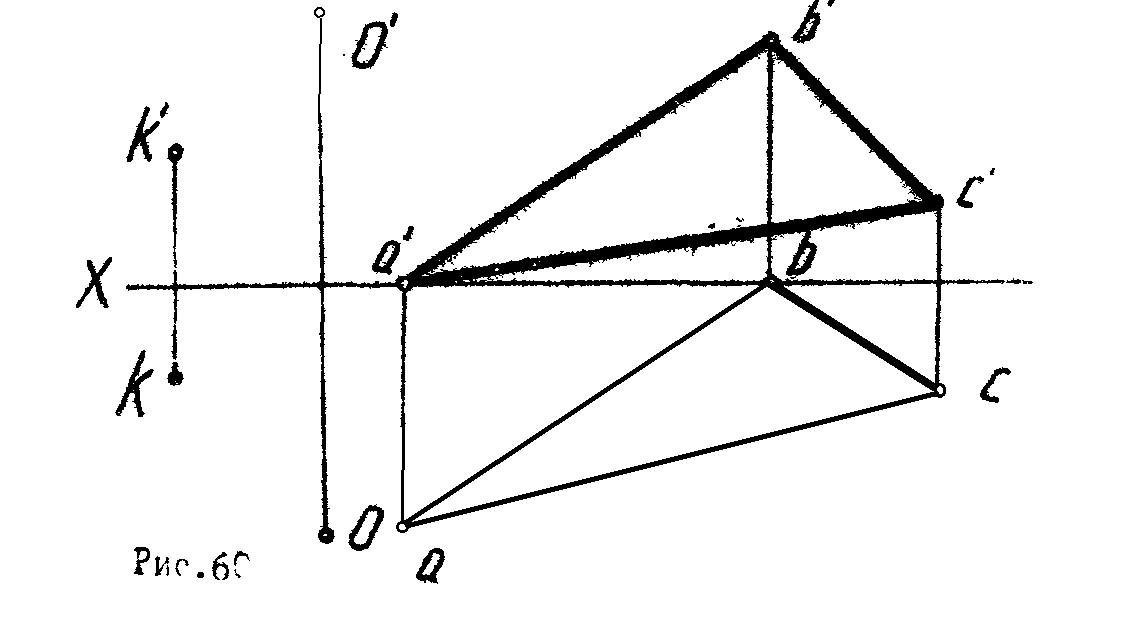
Рис. 60
4.* Определить расстояние от точки К до плоскости (АВС) способом плоско - параллельного перемещения (рис. 61).
5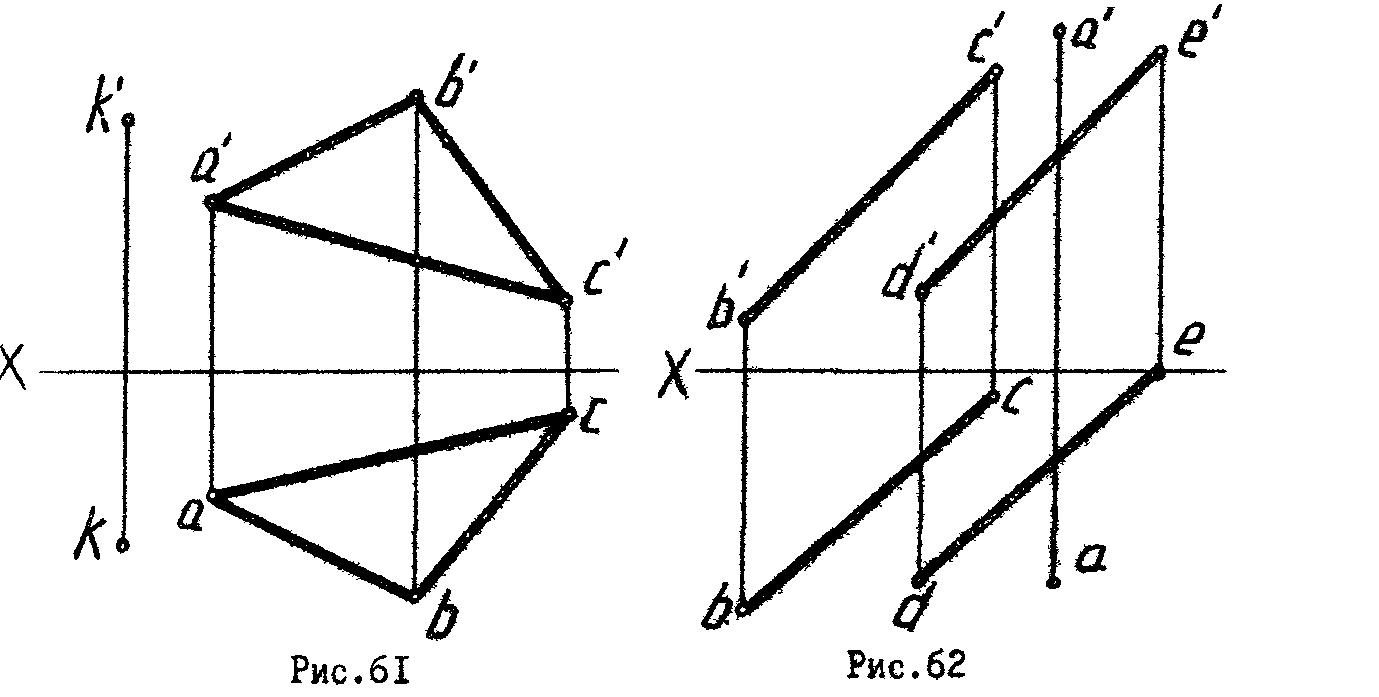
. Способом плоско - параллельного перемещения определить расстояние от точки А до плоскости (ВС||DE) и построить проекции перпендикуляра (рис.62).
6. Найти кратчайшее расстояние между скрещивающимися прямыми АВ и СD (рис.63).
7
*. Способом плоско- параллельного перемещения определить величину двугранного угла при ребре АВ (рис .64)
ТЕМА 10
В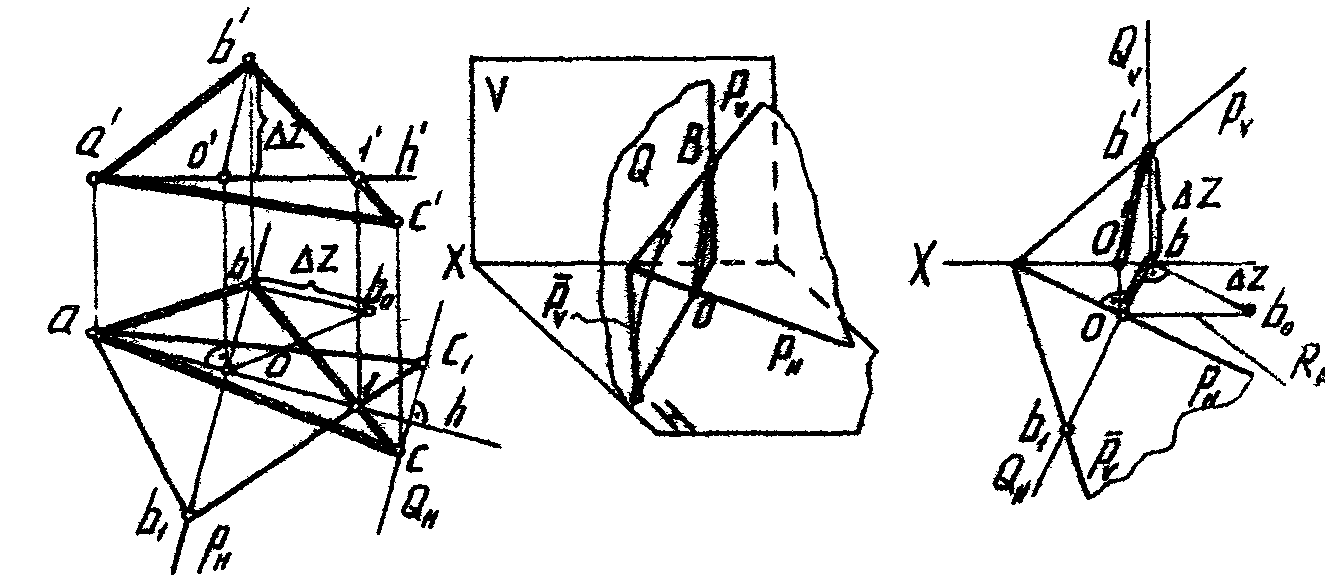
РАЩЕНИЕ ВОКРУГ ЛИНИИ УРОВНЯ, СОВМЕЩЕНИЕ
Вращение вокруг Совмещение (вращение вокруг
горизонтали горизонтального следа)
Чтобы повернуть точку В вокруг горизонтали, необходимо на эпюре определить следующие элементы вращения:
ось вращения в данном примере горизонталь;
плоскость вращения точки В горизонтально проецирующая плоскость Р , перпендикулярная оси вращения;
центр вращения - точка О , которая определяется как точка пересечения оси А1 с плоскостью вращения Р;
радиус вращения R0 величина его определяется как натуральная величина отрезка OВ по правилу прямоугольного треугольника (R0 = Ob0).
Горизонтальную проекцию b1 повернутой точки В находят, отложив от точки О по Рн отрезок, равный R0.
Способ совмещения является частным случаем вращения вокруг линии уровня. В этом способе осями вращения являются нулевые линии уровня следы. Построения аналогичны описанным выше.
1. Определить натуральную величину треугольника АВС (рис.65).
2
. Совместить заданную плоскость с горизонтальной плоскостью проекций (рис .66)
3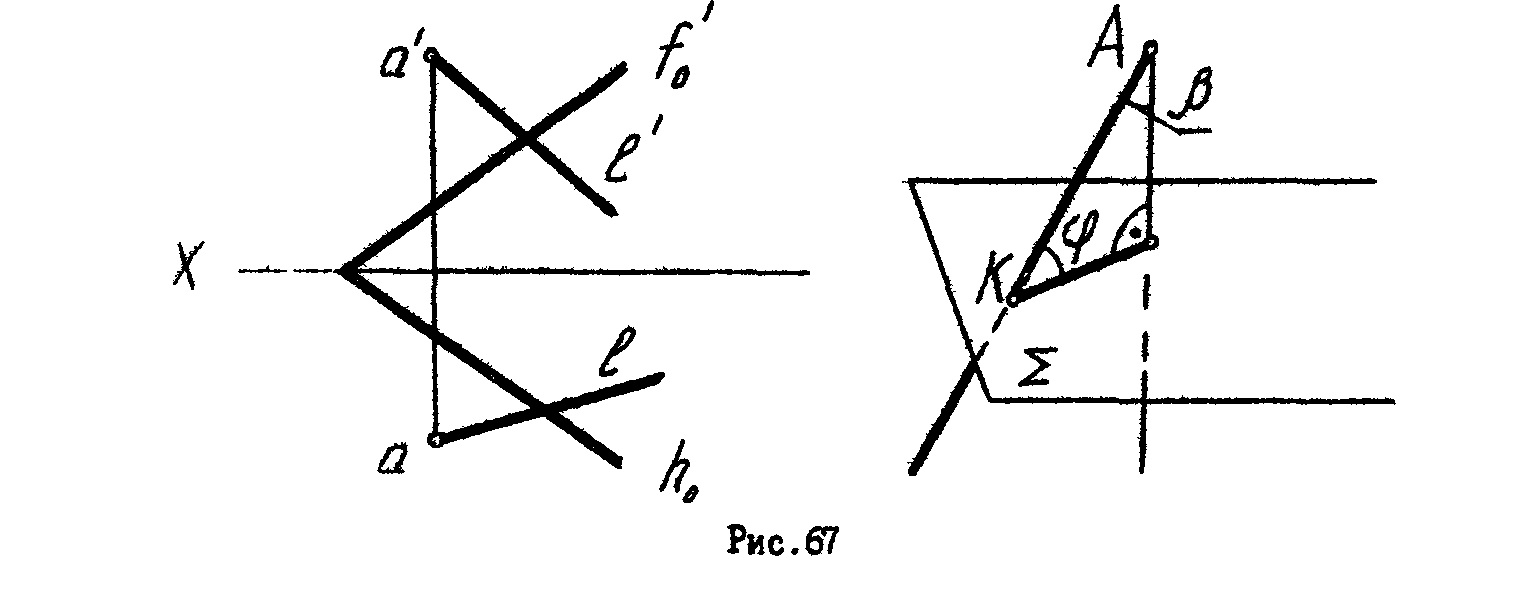
*. Определить натуральную величину угла между прямой и плоскостью (f0 h0) (рис.67).
4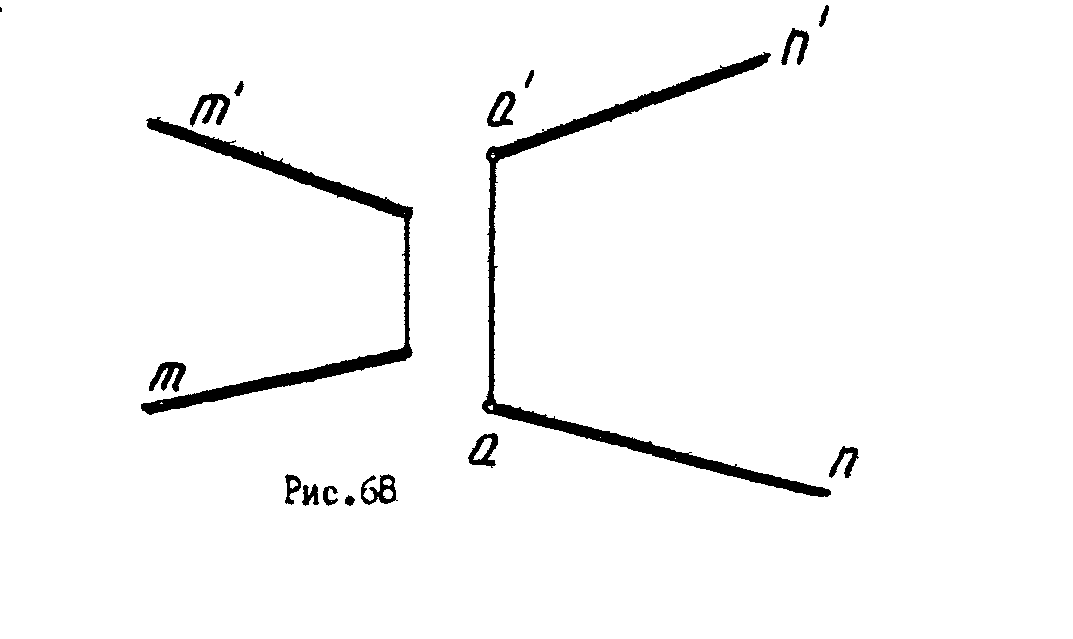
. Определить угол между прямыми m и n (рис.68).
5. Построить проекции равностороннего треугольника АВС, лежащего в плоскости (h0 f0)(рис. 69).
6
.* Построить проекции точки, лежащей в плоскости (h0 f0) по совмещенному положению (рис.70).
7.* Определить величину угла между двумя плоскостями с помощью дополнительного угла (рис.71).
8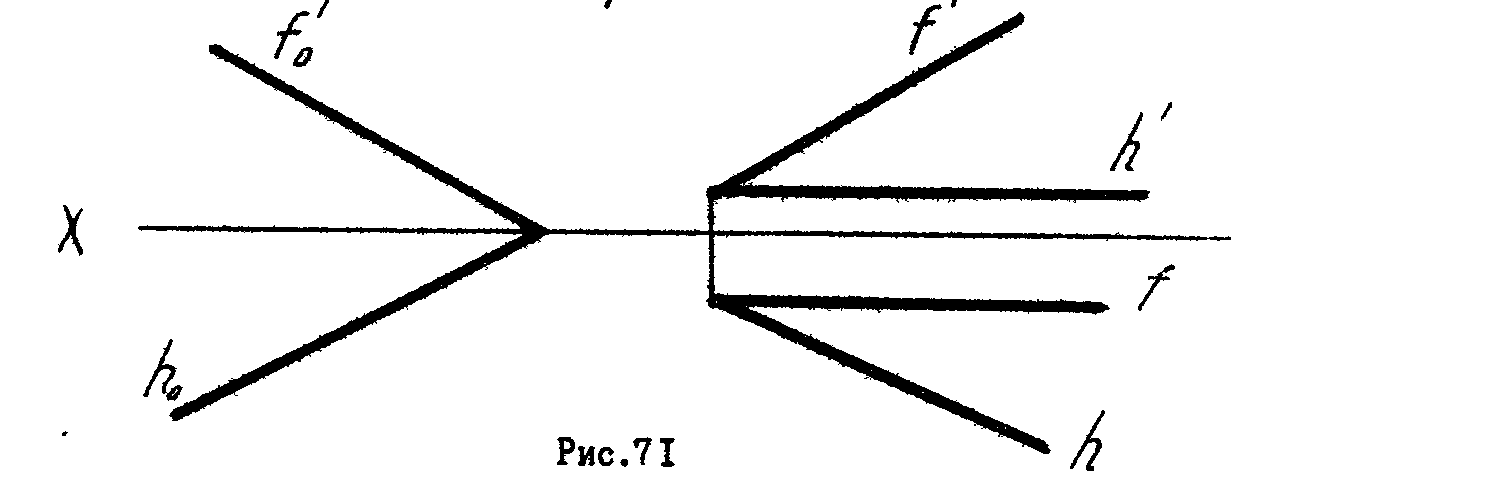
. Построить фронтальные проекции прямых m и n, если угол между ними прямой и ось вращения h(рис.72).

ТЕМА 11
КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ
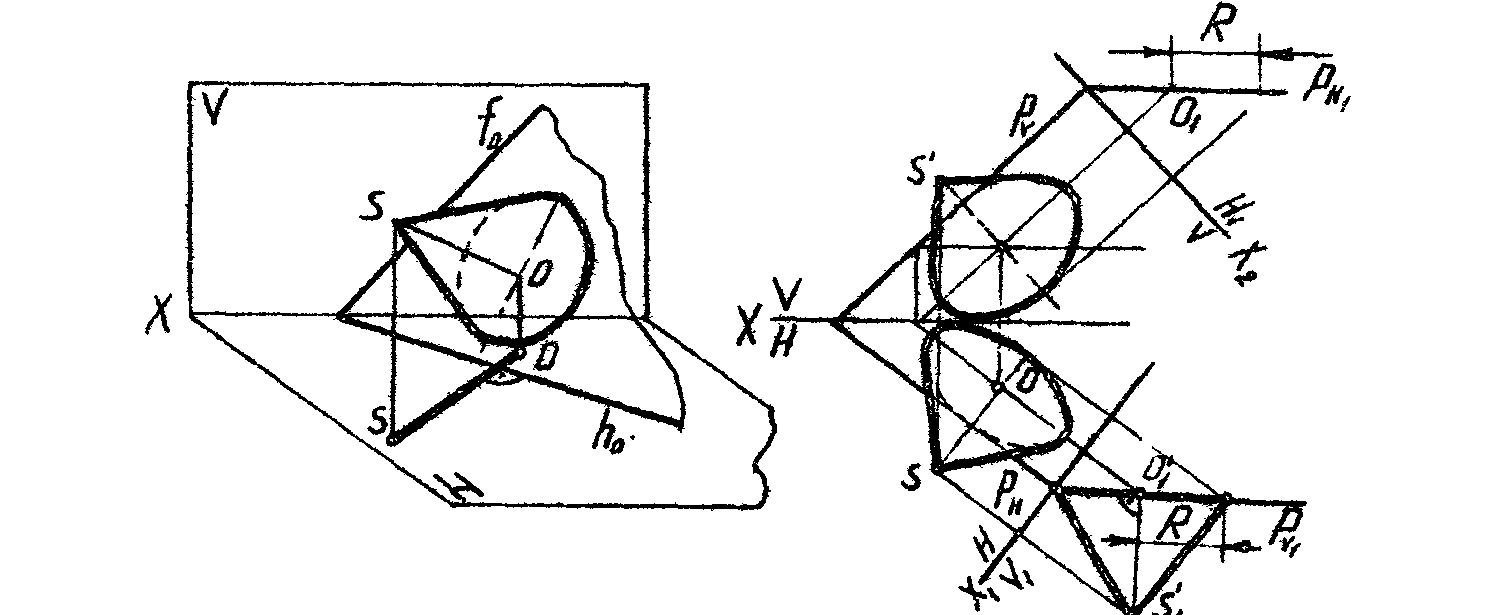
Одной из наиболее распространенных плоских кривых является окружность. Если окружность расположена в плоскости общего положения, то на все плоскости проекций она спроецируется эллипсами. Каждый эллипс строится самостоятельно, т.к. оси эллипсов на разных плоскостях проекций являются проекциями разных диаметров окружности.
Направление большой оси эллипса на Н совпадает с направлениемh, а на V с направлением f’ горизонтали и фронтали плоскости окружности.
Величина большой оси эллипса равна диаметру окружности, а размер малой оси зависит от наклона плоскости окружности к данной плоскости проекций и является разным для каждой из проекций. Размер малой оси удобно определять заменой плоскостей проекций, преобразовывая плоскость окружности в проецирующую.
Ось прямого конуса (или цилиндра), основанием которого является окружность, всегда перпендикулярна к плоскости окружности, и на эпюре ее проекции совпадают по направлению с малыми осями эллипсов.
Размер высоты конуса (или цилиндра.) проецируется в натуральную величину на плоскость проекций V1. По этой проекции строятся проекции высоты в заданной системе.
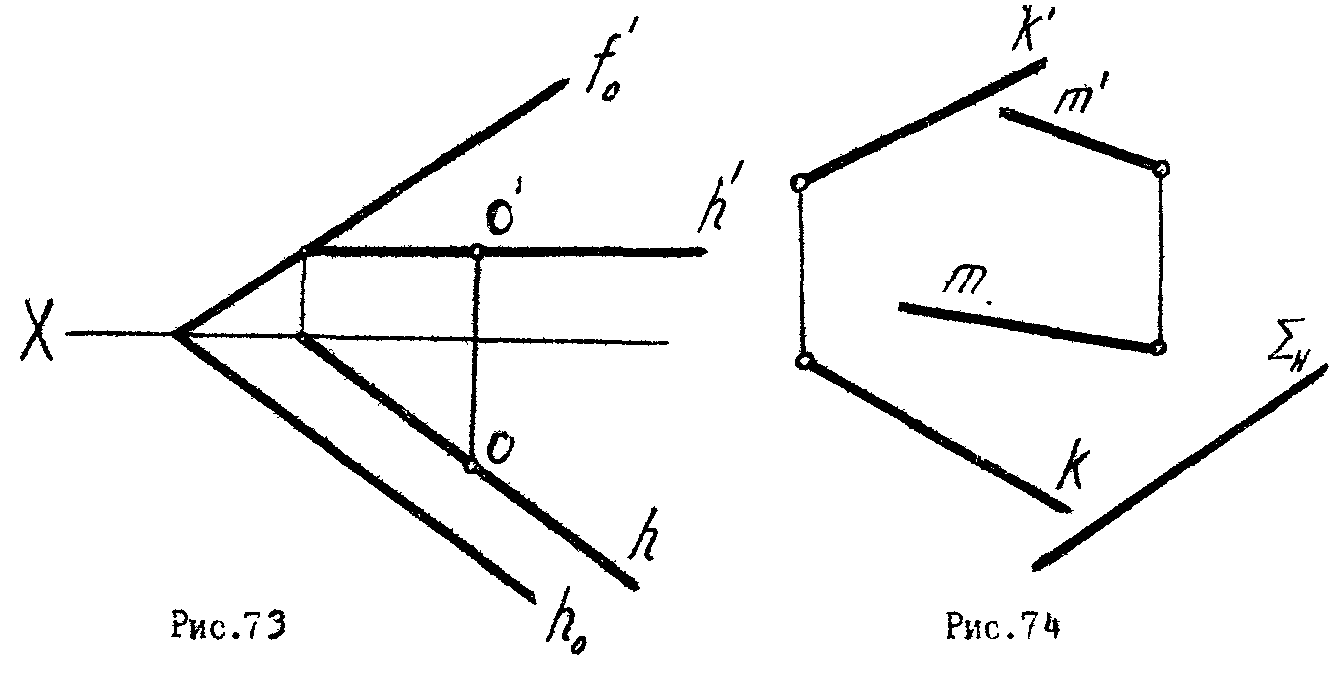
1. Построить окружность диаметром 24 мм с центром 0 , лежащую в заданной плоскости (рис.73).
2. Построить проекции косой плоскости, образованной перемещением образующей по двум направляющим К и m и имеющей плоскостью параллелизма горизонтально - проецирующую плоскость (h) (рис. 74).
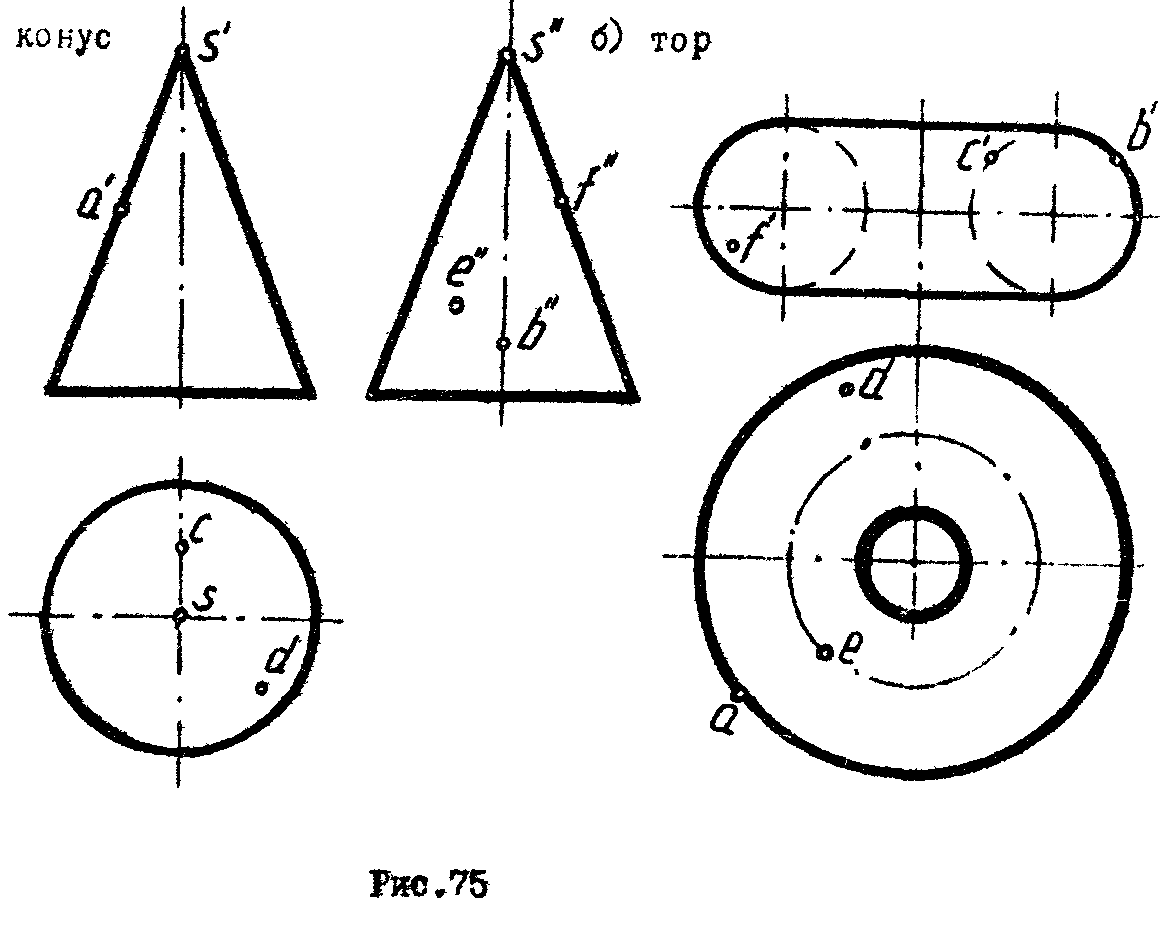
3. Построить отсутствующие проекции точек, лежащих на поверхностях (рис.75 а,б,в,г,д,е).
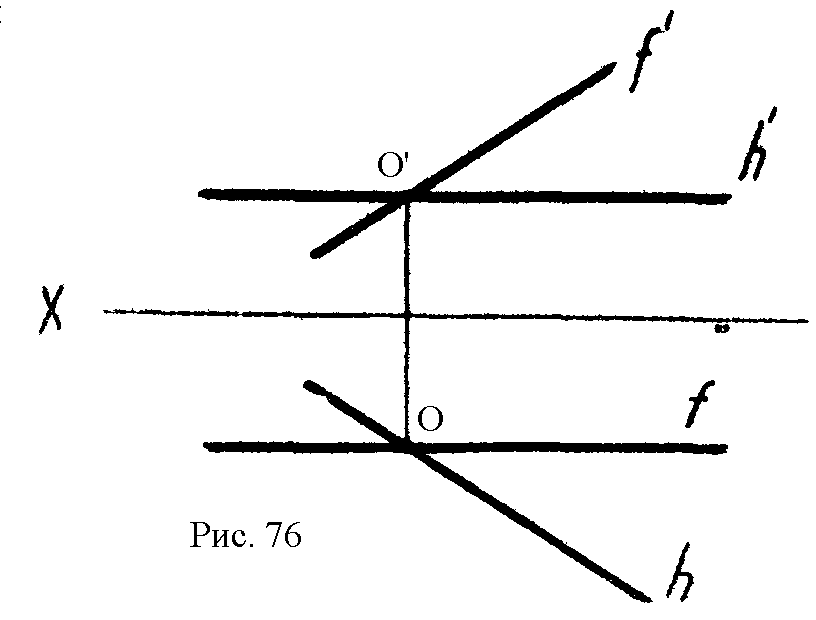
4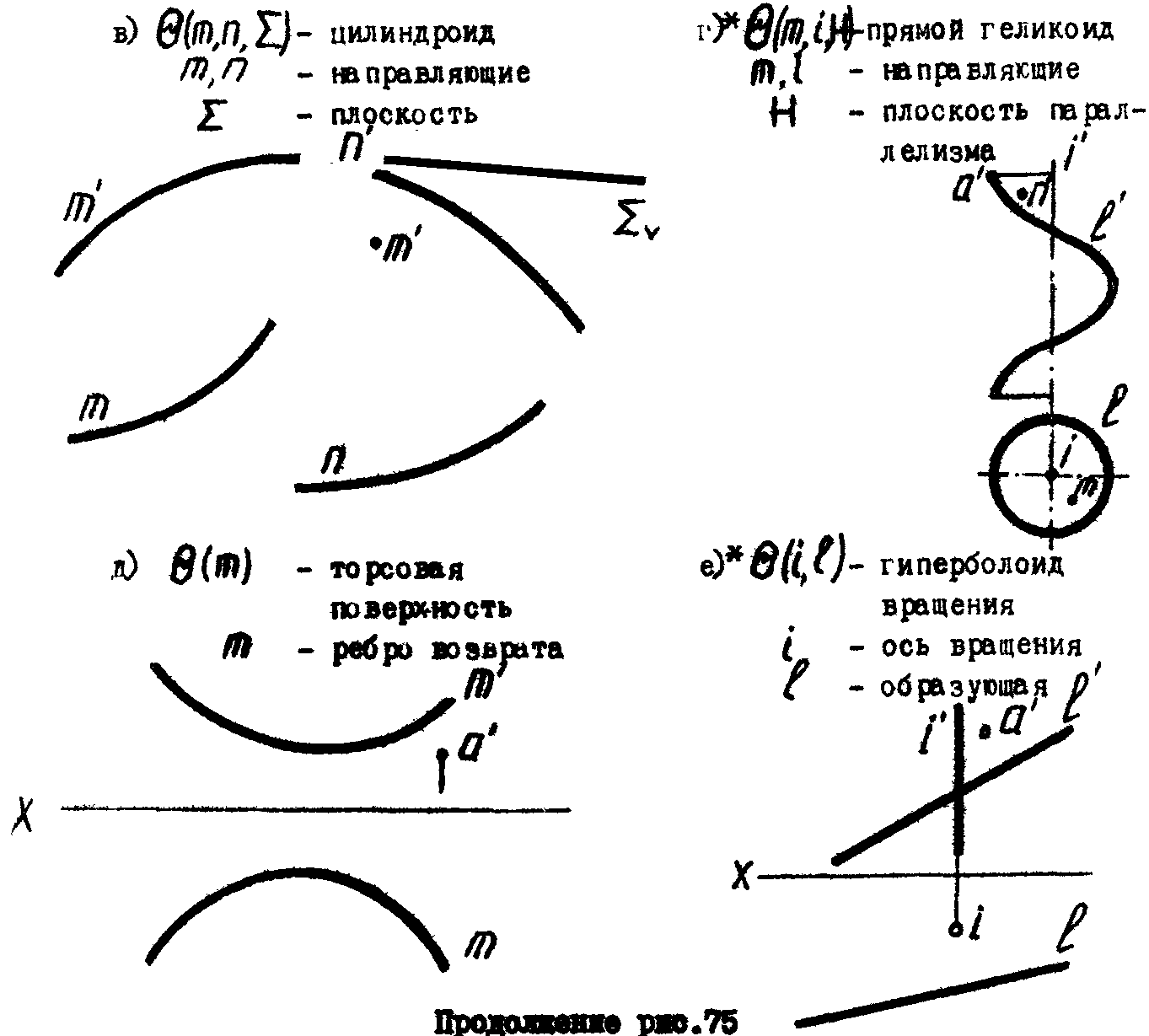
.* Поставить на плоскость (h f) прямой круговой конус высотой 40мм и круговым основанием диаметром 30 мм с центром в точке 0 (рис. 76).
ТЕМА 12
СЕЧЕНИЕ ПОВЕРХНОСТЕЙ ТЕЛ ПЛОСКОСТЬЮ. РАЗВЕРТКИ
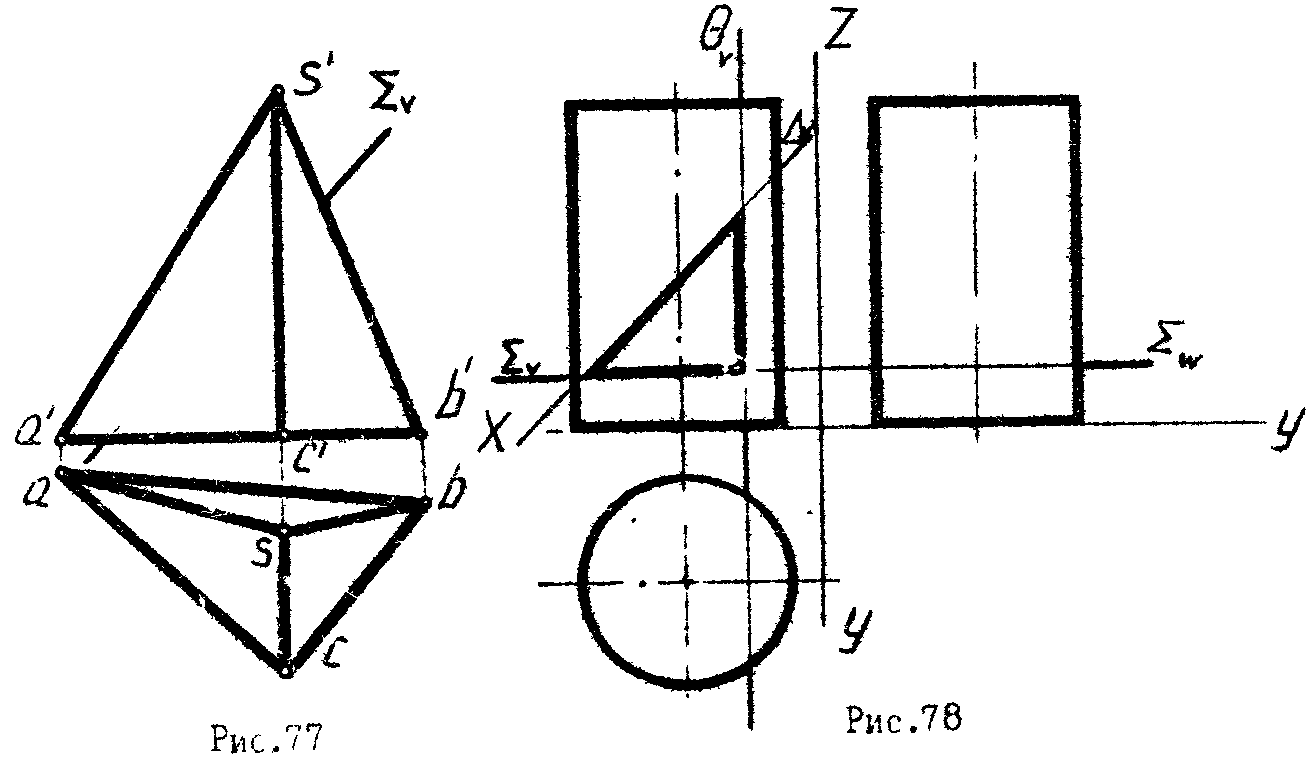
Сечение пирамиды плоскостью Сечение конуса плоскостью
При сечении многогранника плоскостью образуется замкнутая ломаная линия, при пересечении поверхностей вращения плоскостями получаются в общем случае плоские кривые. Для построения этих линий удобно воспользоваться способом замены плоскостей проекций. Преобразовав секущую плоскость в проецирующую, на новой плоскости проекции получают точки искомой линии пересечения как точки пересечения следа - проекции секущей плоскости с ребрами или образующими поверхности тела. Эти точки по линиям связи возвращаются в первоначальную систему плоскостей проекций и соединяются в определенной последовательности с учетом видимости участков линии сечения.
Разверткой называется фигура, полученная при совмещении поверхности всеми ее точками (без складок и разрывов) с плоскостью. Развертка пирамиды выполняется путем последовательного построения натуральной величины треугольников боковых граней. Развертку призмы выполняют способом нормального сечения. Этот способ основан на том, что стороны фигуры нормального сечения развертываются в прямую линию, перпендикулярную ребрам призмы.
Развертку конуса и цилиндра получают, вписав в эти поверхности пирамиду и призму и развернув их, как указано выше.
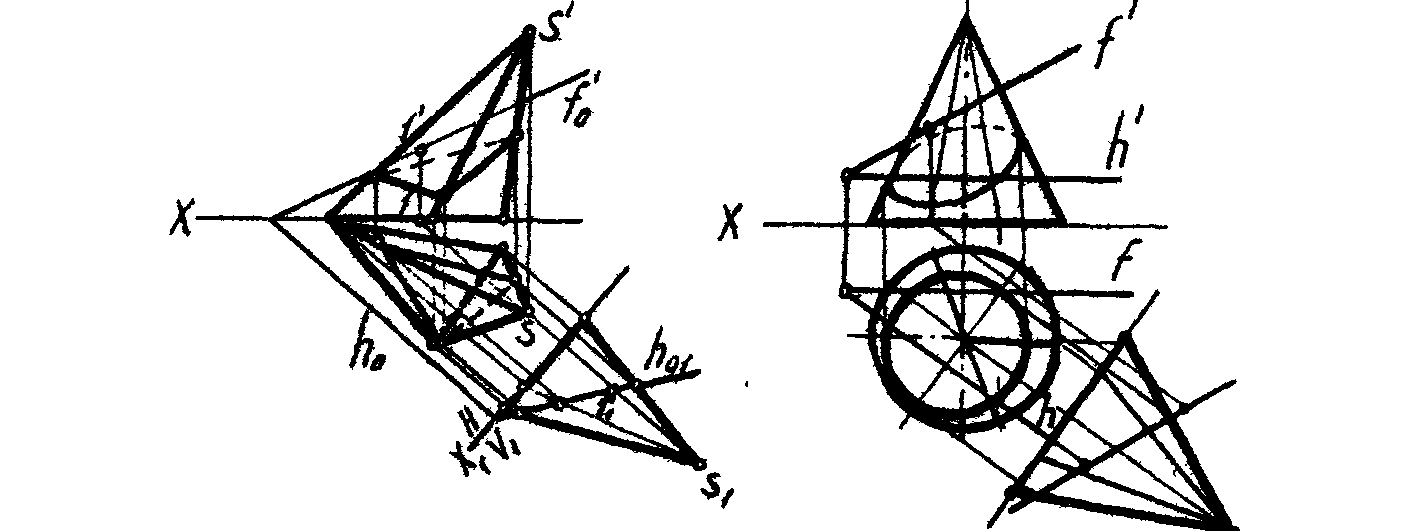
1. Построить проекции линии пересечения поверхности тел проецирующей плоскостью (рис. 77)
2*. Построить три проекции линии пересечения боковой поверхности цилиндра проецирующими плоскостями , , . Назвать указанные плоскости и полученные кривые сечения. Построить развертку боковой поверхности цилиндра с нанесением линии выреза (рис. 78).
3. Построить проекции и натуральную величину сечения призмы плоскостью (АВС) (рис. 79).
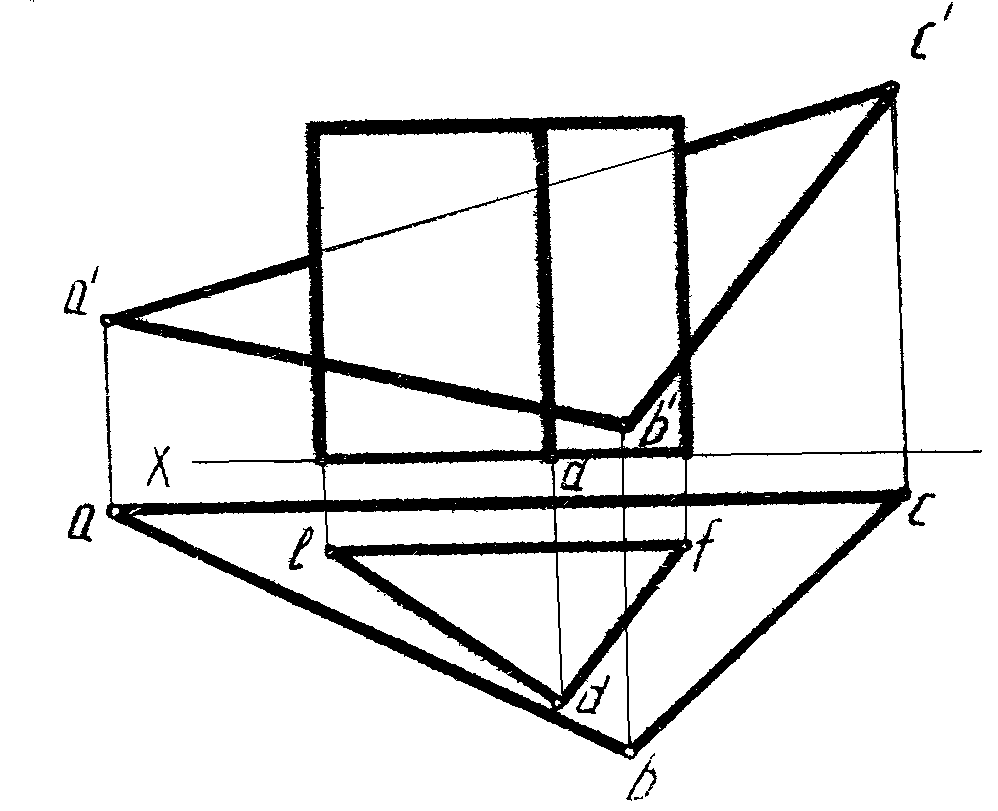
Рис. 79
4. Построить три проекции линии пересечения конуса проецирующими плоскостями ,,. Назвать линии конических сечений (рис.80).
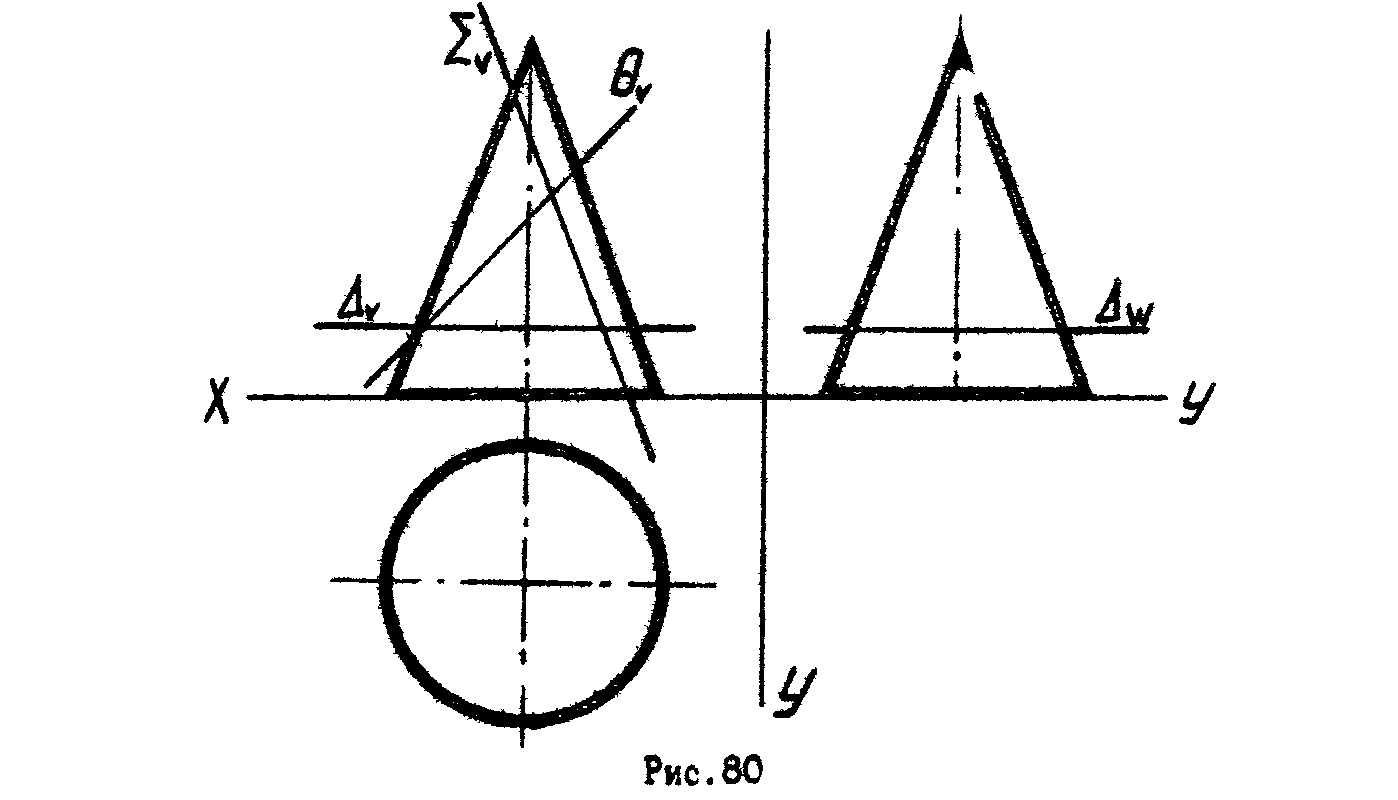
5*. Построить проекции линии сечения поверхности тела плоскостью общего положения и определить натуральную величину сечения (рис.81).

ТЕМА 13
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ
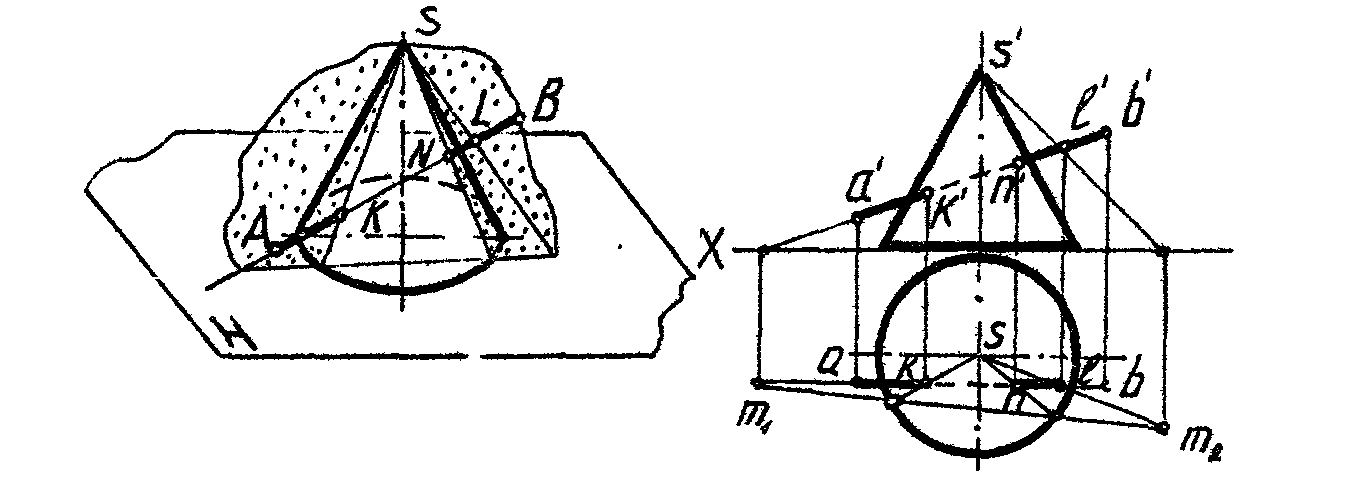
Пересечение прямой с поверхностью конуса
Для определения точек пересечения прямой с поверхностью тела прямую заключают во вспомогательную плоскость, строят линию пересечения поверхности тела этой плоскостью и отмечают точки пересечения найденной линии с данной прямой. Это искомые точки.
Когда прямая пересекает многогранник или сферу, в качестве вспомогательной применяют проецирующую плоскость. Если задан конус или наклонный цилиндр, прямую заключают во вспомогательную плоскость общего положения, которая рассечет поверхность тела по прямолинейным образующим.
Чтобы вспомогательная плоскость рассекла поверхность цилиндра по образующим, она должна включать в себя прямую, параллельную образующим цилиндра. Чтобы вспомогательная плоскость рассекла поверхность конуса по образующим, она должна включать прямую, проходящую через вершину конуса. Образующие сечения на поверхности конуса и цилиндра проходят через точки пересечения кривой основания тела со следом вспомогательной секущей плоскости.
1. Построить проекции точек пересечения прямой с поверхностью многогранника (рис.82).
2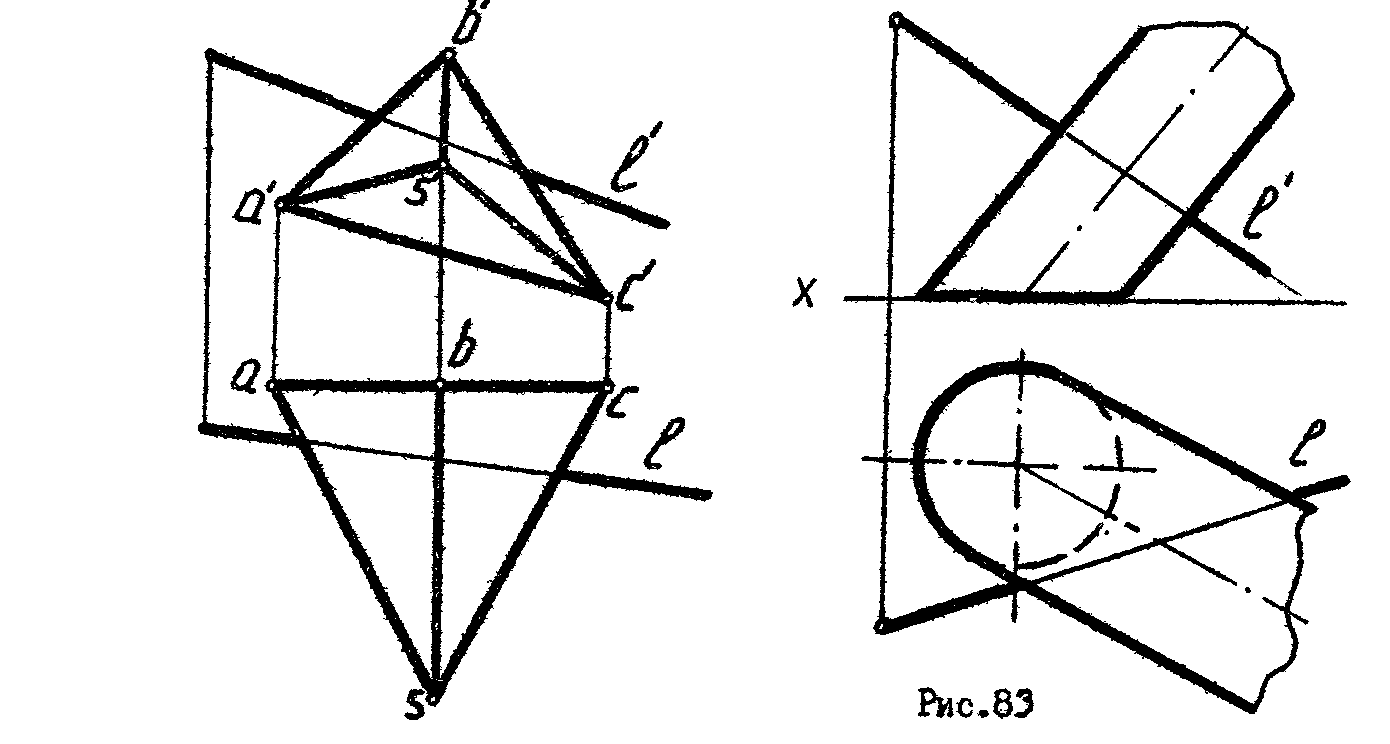
. Определить точки пересечения прямой с поверхностью цилиндра (рис.83).
Рис. 82
3*.Определить точки пересечения прямой с поверхностью шара (рис. 84).
4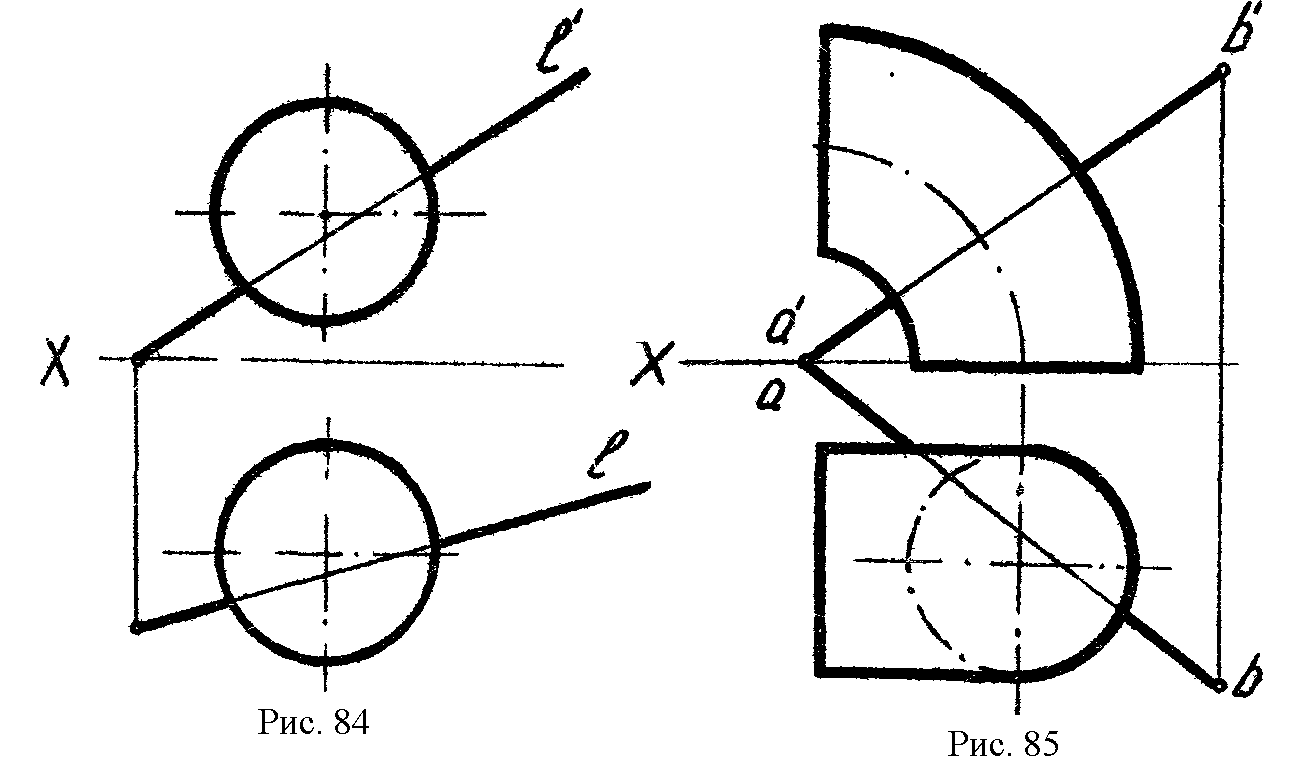
*.Определить точки пересечения прямой с поверхностью тора (рис.85).
ТЕМА 14
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

Пересечение Способ плоскостей Способ сферических
многогранников посредников посредников
В пересечении двух многогранников получаются одна или две замкнутые пространственные ломаные линии, состоящие из отрезков прямых, пересекающихся между собой на ребрах многогранника.
В пересечении двух кривых поверхностей получаются в общем случае одна или две пространственные замкнутые плавные кривые (в частных случаях они распадаются на плоские кривые или даже прямые линии).
Строят линию пересечения по отдельным точкам. Общим способом построения этих точек является способ поверхностей посредников. Пересекая данные поверхности некоторой вспомогательной поверхностью и определяя линии пересечения ее с обеими данными поверхностями, в пересечении этих линий получают точки, принадлежащие искомой линии пересечения.
Выбирают посредники так, чтобы линии их пересечения с данными поверхностями были наиболее, простыми, например, прямыми или окружностями.
В зависимости от характера пересекающихся поверхностей в качестве посредников могут быть приняты плоскости частного положения, сферические поверхности и др.
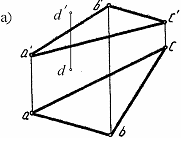
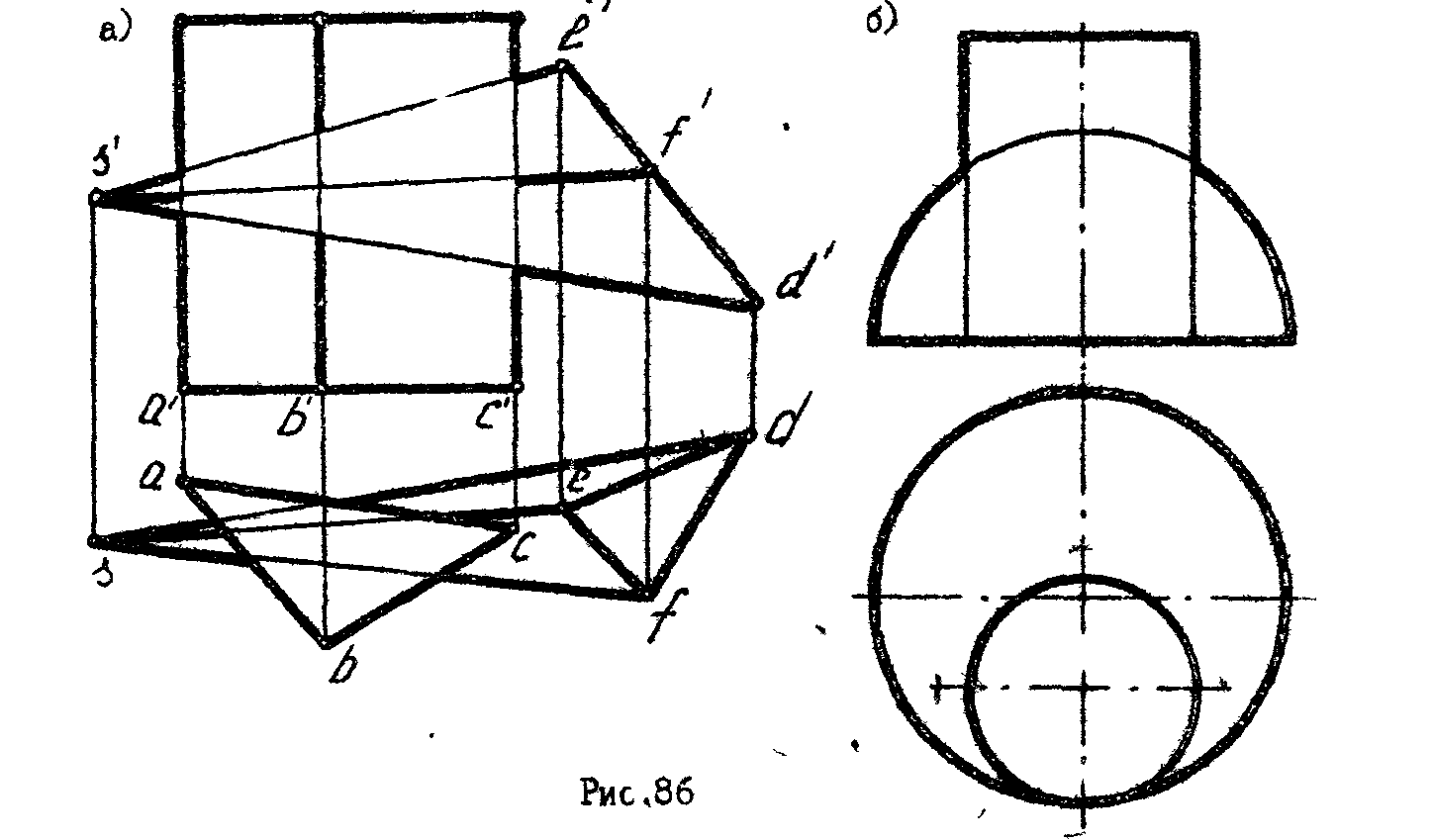
1. Построить проекции линии пересечения двух тел (рис.86 а,б).
2
.* Построить три проекции линии взаимного пересечения двух поверхностей (рис .87).
3
*. Построить проекции линии пересечения двух тел (рис.88 а,б).
4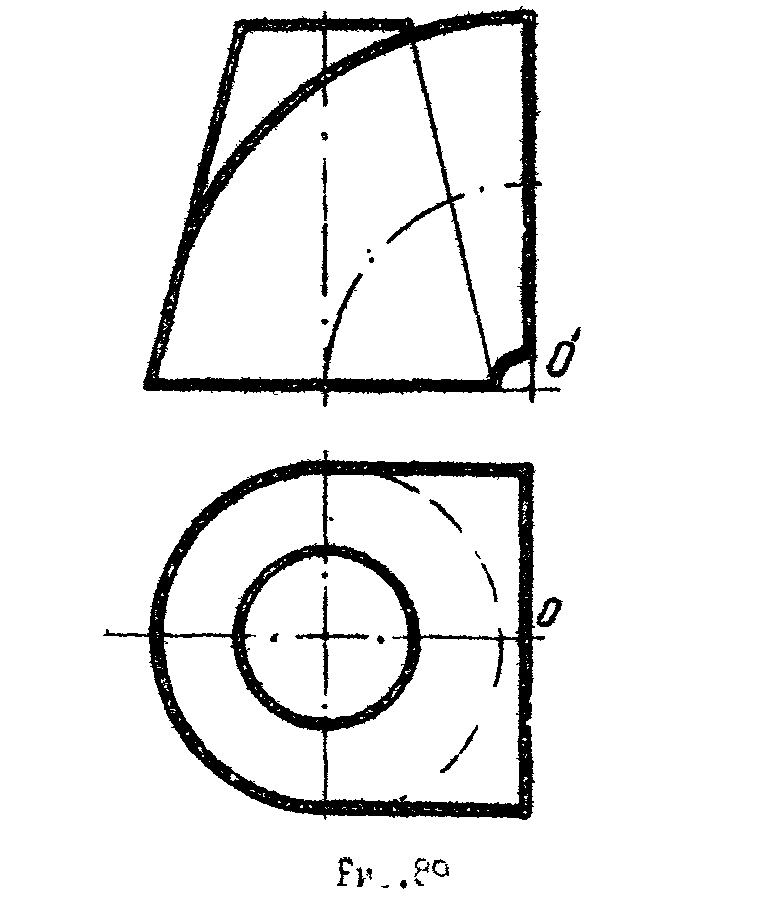
.* Построить проекции линии пересечения конусе и тора (рис.89).
Рис. 89
Литература:
1. Гордон В.О. Начертательная геометрия. – М.: Высш. шк., 2002.
2. Гордон В.О. Сборник задач по курсу начертательной геометрии. – М.: Высш. шк., 2003.
3. Стрижаков А.В. и др. Начертательная геометрия: Учеб. пос. для вузов. Ростов н/Д: Феникс, 2004.
Содержание:
Тема 1. Точка и ее проекции 3
Тема 2. Прямая, ее проекции и следы 7
Тема 3. Взаимные положения прямых 10
Тема 4. Плоскость. Прямая и точка в плоскости 13
Тема 5. Взаимное положение двух плоскостей.
Взаимное положение прямой и плоскости 16
Тема 6. Перпендикулярность прямой и плоскости,
двух плоскостей 20
Тема 7. Геометрические места 23
Тема 8. Способ замены плоскостей проекций 26
Тема 9. Способ вращения вокруг проецирующей оси.
Плоско – параллельные перемещения 29
Тема 10. Вращение вокруг линии уровня, совмещение 32
Тема 11. Кривые линии и поверхности 35
Тема 12. Сечение поверхностей тела плоскостью.
Развертки 38
Тема 13. Пересечение прямой линии с поверхностью 41
Тема 14. Взаимное пересечение поверхностей 43
Литература 46
Бумага офсетная. Формат 60х84 1/16.
Гарнитура «Таймс». Печать трафаретная. Усл.печ. л. 2,6.
Тираж 50 экз. Заказ № 68.
Отпечатано: филиал ГОУ ВПО УГНТУ в г.Стерлитамаке,
453118, РБ, г.Стерлитамак, пр.Октября, 2. |
|
|
 Скачать 3.92 Mb.
Скачать 3.92 Mb.