Расчет системы смазки. 2-Расчет системы смазки ВРД. Национальная Академия Авиации
 Скачать 1.82 Mb. Скачать 1.82 Mb.
|
|
Национальная Академия Авиации Кафедра ЛА и АД РАСЧЁТ СИСТЕМЫ СМАЗКИ ВРД Домашняя работа по дисциплине «Проектирование силовых установок» Выполнил: Принял: Баку- 2021 Содержание 1. Введение 2-4 2. Основные понятия и расчётные формулы 4-12 3. Расчёт гидравлической системы 12-37 4. Таблицы итогов расчёта 37-53 5. Графическая часть 0 6. Список использованной литературы 0 Введение Гидравлические системы широко применяются в технике, например в летательных аппаратах, системах водоснабжения или отопления промышленных предприятий и жилых домов, транспортировки жидкости от места её добычи или хранения к потребителю (транспортировка нефти по нефтепроводам), в пожарных системах и т. д. Все перечисленные системы имеют сходный принцип работы, основанный на законах гидравлики. Гидравлическая система представляет собой набор гидравлических элементов, которые соединены в определённом порядке, обусловленном назначением и пространственным расположением системы. Гидравлическими элементами являются трубопроводы, баки, насосы, всевозможные виды местных сопротивлений. Обычно система имеет; гидравлические элементы, предназначенные для хранения жидкости (баки), передачи жидкости на расстояние (трубопроводы), очистки жидкости (фильтры), управления потоком жидкости (краны, вентили, клапаны, заслонки, термостаты), измерений (расходомеры различных типов), изменения направления или разделения потока жидкости (колена, отводы, тройники, коллекторы), изменения скорости потока жидкости (сужения, расширения), поддержания постоянного уровня жидкости (поплавковые камеры), дозирования и организации истечения жидкости (жиклеры, форсунки, распылители). Гидравлические системы бывают разомкнутыми и замкнутыми (циркуляционными). Система может иметь или не иметь насос (разомкнутая самотечная или замкнутая термосифонная система). Магистраль, по которой жидкость поступает к насосу, называется всасывающей, а магистраль, по которой жидкость движется от насоса, - нагнетающей или напорной. Система смазки ВРД. Система смазки ВРД предназначена для смазки и охлаждения подшипников опор роторов, зубчатых колес редукторов, приводов, шлицевых соединений рессор. Элементов соединительных муфт и т. д. Масло из бака 1 подается насосом 13 к узлам опор, расположенных в разных местах двигателя. К подшипникам масло подводится струйными форсунками 23, 29, 33. Особенностью системы является то, что масло обладает большой вязкостью. Поэтому скорость движения масла в трубопроводах системы смазки обычно меньше, чем в трубопроводах других гидравлических систем, где рабочим телом является вода, керосин или бензин. При расчете этой системы, давление в масленом баке можно принять равным атмосферному давлению 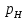 на высоте полета H. Температура масла дана в задании. Давление среды, в которой работают подшипники, можно считать равным атмосферному давлению на высоте полета H. Температура масла дана в задании. Давление среды, в которой работают подшипники, можно считать равным атмосферному давлению 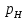 . . Основные понятия и расчётные формулы. В гидравлике рассматриваются одномерные движения жидкости, а сложный многомерный характер учитывается при использовании эмпирических коэффициентов. Можно сказать, что гидравлика является прикладной наукой, в которой решение доводится до вида, удобного для инженерного применения. Нужно отметить, что гидравлика изучает движение капельных жидкостей, т.е. таких жидкостей, которые в малых количествах под действием поверхностного натяжения принимает сферическую форму, а в больших – образуют свободную поверхность раздела с газом. Важным свойством капельных жидкостей является то, что они ничтожно мало изменяют свой объём при изменении давления. Поэтому их считают несжимаемыми. Отсюда можно сделать вывод, что гидравлика рассматривает движение несжимаемой жидкости, т.е. уравнения движения и энергии являются зависимыми и для решения задач достаточно использовать только два основных уравнения: уравнение неразрывности и уравнение энергии. Уравнения и зависимости записываются для контрольного объёма, представляющего собой неподвижный в пространстве объём, через который протекает жидкости. Поскольку гидравлическая система – в общем случае канал с твёрдыми стенками, направляющими движение жидкости, в качестве контрольного объёма выступает либо вся система в целом, либо её участок, ограниченный входным и выходным сечением. Весь поток жидкости можно разбить на множество элементарных струек с бесконечно малым поперечным сечением, в которых из-за их малости параметры постоянны. Поэтому течение в элементарной струйке является одномерным: параметры зависят только от одной координаты, отсчитываемой вдоль оси струйки. В поперечных сечениях гидравлических элементов вычисляются средние параметры (скорость, давление), при использовании которых течение в гидравлическом элементе становится таким же, как в элементарной струйке. Таким образом, в гидравлике все гидравлические элементы заменяются элементарными струйками. Метод гидравлики – это метод элементарной струйки. Изменение параметров в поперечных сечениях гидравлических элементов учитывается в уравнении энергии коэффициентами осреднения (коэффициентами Кориолиса). Закон сохранения массы в гидравлике записывается в виде уравнения неразрывности. 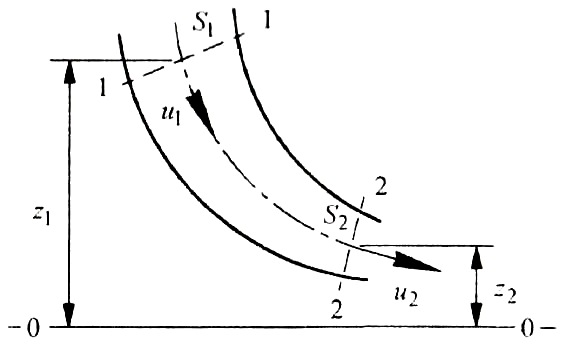 Рис. 1. Участок гидравлической системы с переменным направлением потока жидкости и переменным поперечным сечением Для установившегося режима на участке системы, ограниченном сечениями 1-1 и 2-2 (рис. 1, где 0-0 – плотность сравнения; z – высота сечения канала над плоскостью сравнения), оно записывается в виде: 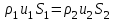 (1) (1)или 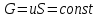 (2) (2)где 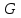 – массовый расход жидкости (масса жидкости, протекающей через поперечное сечение канала в единицу времени), кг/с; – массовый расход жидкости (масса жидкости, протекающей через поперечное сечение канала в единицу времени), кг/с; 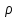 – плотность жидкости, представляющая массу жидкости, заключённую в единице объёма, кг/м3; – плотность жидкости, представляющая массу жидкости, заключённую в единице объёма, кг/м3; 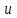 – среднерасходная скорость жидкости в сечении, м/с; – среднерасходная скорость жидкости в сечении, м/с;  – площадь поперечного сечения канала, м2. – площадь поперечного сечения канала, м2.Индексы 1 и 2 в уравнении (1) и в последующих уравнениях обозначают параметры в сечениях входа и выхода соответственно. Для несжимаемой жидкости плотность постоянна в любой точке потока, ввиду чего уравнение неразрывности может быть записано в виде: 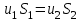 (3) (3)Или 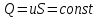 (4) (4)где 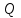 – объёмный расход жидкости, м3/с. – объёмный расход жидкости, м3/с.Из уравнения (4) следует, что объём жидкости, протекающий через все сечения выделенного участка системы в единицу времени, один и тот же. Приведённая запись уравнения неразрывности пригодна для участка, по длине которого нет подвода или отвода жидкости. 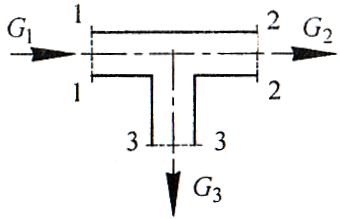 Рис. 2. Участок гидравлической системы с разветвлением потока жидкости Для разветвленного участка, изображённого на рис.2, уравнение неразрывности имеет вид: 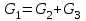 или или 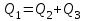 (5) (5)Уравнение энергии в гидравлике записывается в форме, которая называется уравнением Бернулли. Применительно к рис.1 это уравнение записывается следующим образом: 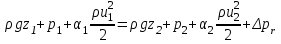 , Па, (6) , Па, (6)где 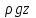 – энергия положения единицы объёма жидкости в сечении, находящемся на высоте – энергия положения единицы объёма жидкости в сечении, находящемся на высоте 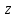 от плоскости сравнения 0-0, Па (см. рис.1); от плоскости сравнения 0-0, Па (см. рис.1); 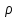 – энергия давления единицы объёма жидкости в сечении, Па; – энергия давления единицы объёма жидкости в сечении, Па; 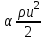 – кинетическая энергия единицы объёма жидкости в сечении, Па; – кинетическая энергия единицы объёма жидкости в сечении, Па; 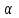 – коэффициент Кориолиса, учитывающий неравномерность распределения кинетической энергии по сечению; – коэффициент Кориолиса, учитывающий неравномерность распределения кинетической энергии по сечению;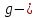 ускорение свободного падения ( ускорение свободного падения (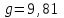 м/с2); м/с2); 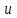 – среднерасходная скорость потока в сечении, м/с; – среднерасходная скорость потока в сечении, м/с; 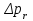 – потери механической энергии единицы объёма жидкости в участке системы, между сечениями 1-1 и 2-2 за счёт местных и (или) путевых сопротивлений, Па. – потери механической энергии единицы объёма жидкости в участке системы, между сечениями 1-1 и 2-2 за счёт местных и (или) путевых сопротивлений, Па.В практических расчетах принимают, что при ламинарном течении в круглой трубе распределение скорости по сечению трубы (профиль скорости) представляет параболу (рис. 3), а коэффициент Кориолиса 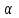 равен 2. При турбулентном течении профиль скорости близок к равномерному и равен 2. При турбулентном течении профиль скорости близок к равномерному и 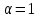 . .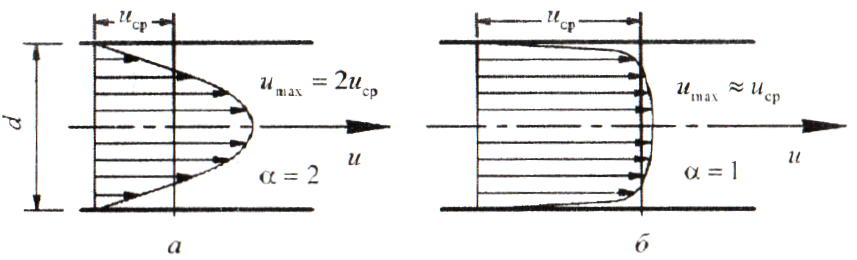 Рис. 3. Профиль скоростей при режимах течения жидкостей в круглой трубе: а) – при ламинарном (Re<2300); б) – при турбулентном (Re>4000) Полное давление (давление торможения) определяется как 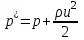 , а величину , а величину 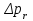 называют потерями полного давления на длине выделенного участка системы. называют потерями полного давления на длине выделенного участка системы.Различают два вида потерь полного давления на гидравлическом сопротивлении – местные и путевые, которые связаны формулой: 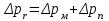 Местные потери проявляются в местах изменения формы, размеров каналов или изменения направления движения потока, вычисляются по формуле Вейсбаха: 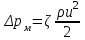 (7) (7)Где 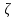 – коэффициент местного сопротивления, значение которого обычно определяется по справочным данным, в которых указывается сечение, определяющее потери; – коэффициент местного сопротивления, значение которого обычно определяется по справочным данным, в которых указывается сечение, определяющее потери; 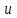 – среднерасходная скорость в определяющем сечении. – среднерасходная скорость в определяющем сечении.Путевые потери – потери полного давления по длине трубы с полной осью. Они вычисляются по формуле Дарси: 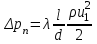 (8) (8)где 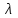 – коэффициент путевых потерь (коэффициент Дарси); – коэффициент путевых потерь (коэффициент Дарси); 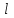 – длина трубы, м; – длина трубы, м; 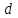 – диаметр трубы, м. – диаметр трубы, м.Значения коэффициента Кориолиса 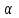 и коэффициентов потерь и коэффициентов потерь 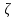 зависят от режима течения жидкости на рассматриваемом участке системы. Различают ламинарный и турбулентный режимы течения. При ламинарном режиме частицы жидкости движутся по почти параллельным траекториям со слабым перемещением слоёв. В турбулентном течении наряду с главным направленным движением частицы жидкости совершают беспорядочные и хаотичные перемещения в продольном и поперечных направлениях. Поэтому турбулентное течение всегда сопровождается интенсивным перемешиванием жидкости и пульсациями скорости и давления. зависят от режима течения жидкости на рассматриваемом участке системы. Различают ламинарный и турбулентный режимы течения. При ламинарном режиме частицы жидкости движутся по почти параллельным траекториям со слабым перемещением слоёв. В турбулентном течении наряду с главным направленным движением частицы жидкости совершают беспорядочные и хаотичные перемещения в продольном и поперечных направлениях. Поэтому турбулентное течение всегда сопровождается интенсивным перемешиванием жидкости и пульсациями скорости и давления. Режим течения жидкости в круглой трубе характеризуется числом Рейнольдса: 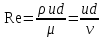 (9) (9)Где 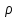 – плотность жидкости, кг/м3; – плотность жидкости, кг/м3; 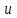 – среднерасходная скорость жидкости в трубе, м/с; – среднерасходная скорость жидкости в трубе, м/с; 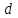 – диаметр трубы, м; – диаметр трубы, м;  – динамический коэффициент вязкости, Па·с; – динамический коэффициент вязкости, Па·с; 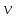 – кинематический коэффициент вязкости, м2/с. – кинематический коэффициент вязкости, м2/с.Динамический коэффициент вычисляется по формуле: 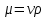 (10) (10)Значения 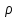 и и  определяются по справочным данным в зависимости от температуры и давления жидкости. В большинстве случаев их зависимостью от давления можно пренебречь. определяются по справочным данным в зависимости от температуры и давления жидкости. В большинстве случаев их зависимостью от давления можно пренебречь.Ламинарный режим течения существует устойчиво при числах Рейнольдса Re ≤ 2300; при Re > 2300 ламинарное течение теряет устойчивость, при 2300 < Re < 4000 существует переходный режим течения, а при Re > 4000 течение становится турбулентным. При ламинарном течении коэффициент путевых потерь определяется по формуле Пуазейля: 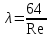 (11) (11)При турбулентном течении на величину потерь влияет не только число Рейнольдса, но и шероховатость внутренней поверхности трубы, При умеренных числах Рейнольдса вблизи стенки трубы течение ламинарное, так как стенка подавляет пульсации скорости. Эта ламинарная плёнка на стенке называется ламинарным пограничным подслоем. Пока ламинарный подслой покрывает бугорки поверхности, бугорки шероховатости, потери обусловлены только внутренним трением в жидкости. Трубы при таком течении называются гидравлически гладкими, а коэффициент путевых потерь вычисляется по формуле Блазиуса: 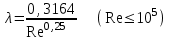 (12) (12)или по формуле Конакова: 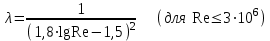 (13) (13)С увеличением числа Рейнольдса ламинарная стенка становится тоньше, высокие бугорки шероховатости выступают из неё и увеличивают сопротивление движению жидкости. Гидравлические потери в этом случае зависят от числа Рейнольдса и относительной шероховатости трубы. Дальнейшее увеличение числа Рейнольдса приводит к разрушению ламинарной стенки и потому величина гидравлических потерь перестаёт зависеть от числа Рейнольдса и определяется только относительной шероховатостью поверхности трубы. Таким образом, одна и та же труба в зависимости от режима течения жидкости может быть гидравлически гладкой или шероховатой. Во многих технических задачах можно полагать, что трубы гидравлически гладкие. Если труба не круглая, то в качестве характерного размера, определяющего число Рейнольдса, вместо диаметра используют гидравлический диаметр: 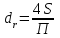 (14) (14)Где  – площадь поперечного сечения трубы, м 2; – площадь поперечного сечения трубы, м 2; 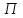 – смоченный периметр, т.е. участок периметра сечения трубы, на котором жидкость соприкасается с её стенками. – смоченный периметр, т.е. участок периметра сечения трубы, на котором жидкость соприкасается с её стенками.Нетрудно показать, что для круглой трубы 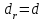 ,так как в этом случае ,так как в этом случае 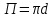 , а , а 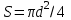 . Для полностью заполненной потоком жидкости трубы прямоугольного сечения формула примет вид: . Для полностью заполненной потоком жидкости трубы прямоугольного сечения формула примет вид: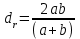 (15) (15)где  и и 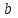 стороны сечения прямоугольной трубы, м. стороны сечения прямоугольной трубы, м.Если труба прямоугольного сечения заполнена потоком жидкости на высоту 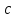 , то формула (15) примет вид: , то формула (15) примет вид: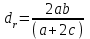 (16) (16)Для кольцевого канала гидравлический диаметр вычисляется по формуле: 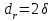 (17) (17)где 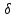 – ширина кольцевого канала, м. – ширина кольцевого канала, м.Расчёт гидравлической системы. 1. Определим теплофизические характеристики рабочей жидкости для температуры +50 °C: Для заданной температуре это осуществляют по справочным данным (см. приложение 3 [1]) - плотность жидкости 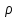 = 875,3 кг/м3; = 875,3 кг/м3;- коэффициент вязкости  = 156,85*10-3 Па*с; = 156,85*10-3 Па*с; |
