63 элементы статистика матем. Национальный социальнопедагогический колледж Специальность
 Скачать 42.11 Kb. Скачать 42.11 Kb.
|
|
Национальный социально-педагогический колледж Специальность: 44.02.01 Дошкольное образование Дисциплина: МАТЕМАТИКА Тема самостоятельной работы: Элементы математической статистики Работу выполнил студент группы: 8 ДО 09/20А-1 Короткевич Снежана Ивановна Работу проверил и принял: Галкина Людмила Сергеевна ________________________ «_____» ______________ 2021 г. Красноярск 2021 Задание 2. Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы? (медиана: ряд записать в порядке возрастания; определить элемент, который делит ряд пополам) Решение. Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить. Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда. Упорядочим данный ряд: 130, 132, 134, 158, 166, следовательно, медиана равна 134. Среднее арифметическое же будет равно Разница между медианой и средним арифметическим составляет 144 − 134 = 10. Ответ: 10. Задание 3. Средний рост жителя города, в котором живет Даша, равен 170 см. Рост Даши 173 см. Какое из следующих утверждений верно? 1) Даша — самая высокая девушка в городе. 2) Обязательно найдется девушка ниже 170 см. 3) Обязательно найдется человек ростом менее 171 см. 4) Обязательно найдется человек ростом 167 см Решение. Первое утверждение неверно: например, в городе могут жить три девушки ростом 162 см, 173 см и и 175 см. Второе утверждение неверно: в городе может жить только одна девушка — Даша, а все остальные жители города могут являться мужчинами. Третье утверждение верно: если все жители будут не ниже 171 см, то средний рост будет не меньше 171 см. Четвёртое утверждение неверно: например, в городе могут жить трое жителей ростом 165 см, 172 см и 173 см. Ответ: 3. Примечание. Заметим, что в ответе надо указать номера только тех утверждений, которые всегда являются верными при заданных условиях. Если можно привести хотя бы одни пример, удовлетворяющий условиям задания, но не удовлетворяющий условиям утверждения, то утверждение не является верным. Такие примеры приведены для утверждений 1, 2 и 4, следовательно, эти утверждения не являются верными. Наличие примера, при котором утверждение является верным, не доказывает, что это утверждение будет верным всегда, поэтому для того, чтобы убедиться в верности утверждения, необходимы логические рассуждения, как показано в решении для утверждения 3. Задание 4. По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города
Построить гистограмму частот Решение: Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей. Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака: Размах вариации размера вклада равен 1000 рублей. 2) Средний размер вклада определим по формуле средней арифметической взвешенной. Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов. Среднее значение первого интервала будет равно: 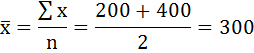 второго - 500 и т. д. Занесём результаты вычислений в таблицу:
Средний размер вклада в Сбербанке города будет равен 780 рублей: 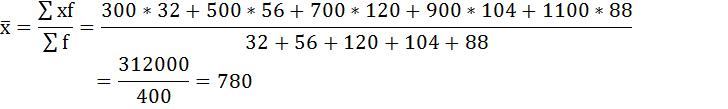 3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней: 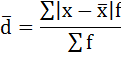 Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий: 1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2). 2. Определяются абсолютные отклонения вариант от средней: 3. Полученные отклонения умножаются на частоты: 4. Находится сумма взвешенных отклонений без учёта знака: 5. Сумма взвешенных отклонений делится на сумму частот: 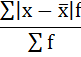 Удобно пользоваться таблицей расчётных данных:
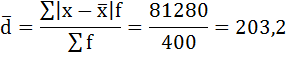 Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля. 4) Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической. Расчёт дисперсии в интервальных рядах распределения производится по формуле: 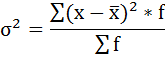 Порядок расчёта дисперсии в этом случае следующий: 1. Определяют среднюю арифметическую взвешенную, как показано в п. 2). 2. Находят отклонения вариант от средней: 3. Возводят в квадрат отклонения каждой варианты от средней: 4. Умножают квадраты отклонений на веса (частоты): 5. Суммируют полученные произведения: 6. Полученная сумма делится на сумму весов (частот): 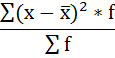 Расчёты оформим в таблицу:
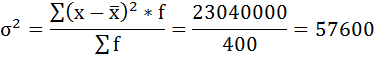 5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии: 6) Коэффициент вариации - это отношение среднего квадратического отклонения к средней арифметической: 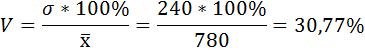 По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Задание 5. Найдите и построить эмпирическую функцию распределения данной выборки
Построить полигон частот. ni называются частотами, найдите их сумму, это будет n (объем выборки) поделите каждое ni на n, это будут относительные частоты (wi) тогда эмпирическая функция распределения будет иметь вид F(x)= 0, x<=2, w1, 2 |
