ПК 1. Надежность элементов, определенная по статистическим данным об отказах устройств

• Название: Надежность элементов, определенная по статистическим данным об отказах устройств
• Дата: 17.04.2023
• Размер: 275.97 Kb.
• Имя файла: ПК 1.docx
• Тип: Лабораторная работа; #1067911
• страница: 3 из 4

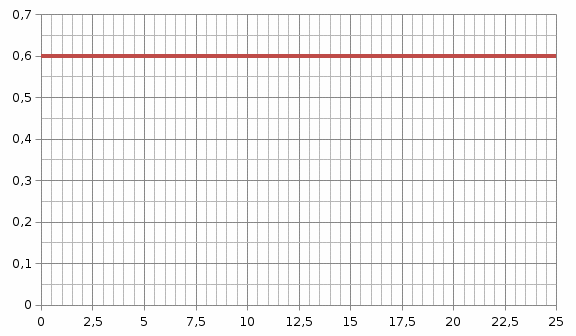в

Рис. 2.1. Влияние параметров экспоненциального закона распределения на вероятность безотказной работы (а), плотность распределения наработки до отказа (б), интенсивность отказов (в).

Вывод: При экспоненциальном законе, на основании полученных зависимостей (рис. 2.1) при увеличении параметра α, уменьшается вероятность безотказной работы, увеличиваются плотность и интенсивность отказов, уменьшается средняя наработка до отказов.

По нормальному закону распределения:

Рассчитаем начальную наработку t_н и наработку t_пр:

t_н = m - 3σ = 4,9 - 3 0,2 = 4,3 ;

t_пр = m + 3σ = 4,9 + 3 0,2 = 5,5

Определим интервал наработки Δt:

Δt = = = 0,12 ч

де k - количество интервалов наблюдения, k =10.

Рассчитаем наработку для всех интервалов наблюдения: t_i = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.

Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа по выражениям:

Р(t) =1 - ;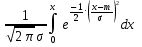

q(t) = ;

λ(t) =

T₀ = m

Результаты расчетов занесем в таблицу 2.2.

Изменим параметр нормального закона распределения, задав его

равным К_пар m и повторить расчет:

m = 4,9 3,0 = 14,7

Рассчитаем начальную наработку t_н и наработку t_пр:

t_н = m - 3σ = 14,7 - 3 0,2 = 14,1 ;

t_пр = m + 3σ = 14,7 + 3 0,2 = 15,3

Определим интервал наработки Δt:

Δt = = = 0,12 ч

де k - количество интервалов наблюдения, k =10.

Рассчитаем наработку для всех интервалов наблюдения: t_i = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.

Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.

Результаты вычислений занесем в таблицу 2.2.

Изменим параметр нормального закона распределения, задав его

равным К_пар σ и повторить расчет: σ = 3 0,2 = 0,6 .

Рассчитаем начальную наработку t_н и наработку t_пр:

t_н = m - 3σ = 4,9 - 3 0,6 = 3,1 ;

t_пр = m + 3σ = 4,9 + 3 0,6 = 6,7

Определим интервал наработки Δt:

Δt = = = 0,36 ч

де k - количество интервалов наблюдения, k =10.

Рассчитаем наработку для всех интервалов наблюдения: t_i = iΔt, где i – номер интервала наработки, ч, i = 0, 1, …10.

Определим вероятность безотказной работы P(t), частоту отказов q(t), интенсивность отказов λ(t) и среднюю наработку до отказа.

Результаты вычислений занесем в таблицу 2.2.

Таблица 2.2 Результаты расчетов

Интервал наблюдений, i	Параметры закона распределения
	Первоначальные параметры закона распределения
	ti, 103ч	P(t)	q(t), 10-3/ч	λ(t), 10-3/ч	Т0, 103ч
0	4,3	0,99865	0,022159242	0,022189195	4,9
1	4,42	0,991802	0,111972651	0,112898138
2	4,54	0,96407	0,394750792	0,409462925
3	4,66	0,88493	0,970930275	1,09718273
4	4,78	0,725747	1,666123014	2,295735683
5	4,9	0,5	1,994711402	3,989422804
6	5,02	0,274253	1,666123014	6,075128801
7	5,14	0,11507	0,970930275	8,437760124
8	5,26	0,03593	0,394750792	10,98656514
9	5,38	0,008198	0,111972651	13,65930598
10	5,5	0,00135	0,022159242	16,41549327
Измененный параметр m
0	14,1	0,99865	0,022159	0,022189195	14,7
1	14,22	0,991802	0,111973	0,112898138
2	14,34	0,96407	0,394751	0,409462925
3	14,46	0,88493	0,97093	1,09718273
4	14,58	0,725747	1,666123	2,295735683
5	14,7	0,5	1,994711	3,989422804
6	14,82	0,274253	1,666123	6,075128801
7	14,94	0,11507	0,97093	8,437760124
8	15,06	0,03593	0,394751	10,98656514
9	15,18	0,008198	0,111973	13,65930598
10	15,3	0,00135	0,022159	16,41549327
Измененный параметр σ
0	3,1	0,99865	0,007386414	0,007396398	4,9
1	3,46	0,991802	0,037324217	0,037632713
2	3,82	0,96407	0,131583597	0,136487642
3	4,18	0,88493	0,323643425	0,365727577
4	4,54	0,725747	0,555374338	0,765245228
5	4,9	0,5	0,664903801	1,329807601
6	5,26	0,274253	0,555374338	2,025042934
7	5,62	0,11507	0,323643425	2,812586708
8	5,98	0,03593	0,131583597	3,662188381
9	6,34	0,008198	0,037324217	4,553101993
10	6,7	0,00135	0,007386414	5,471831092

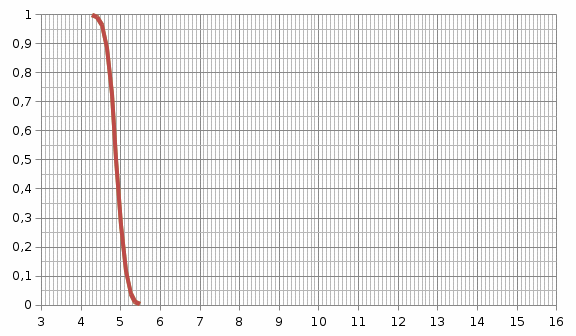а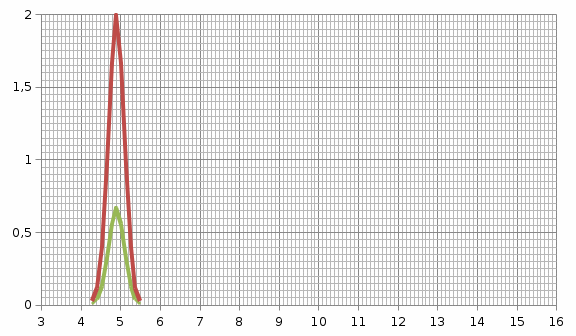



б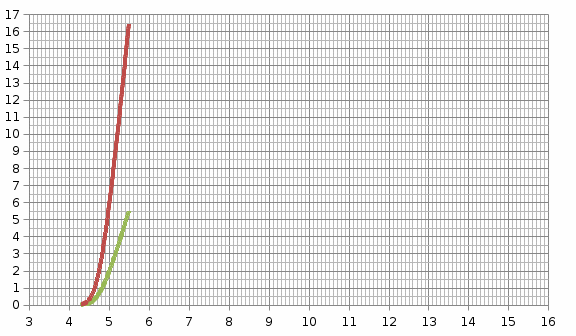


в

Рис. 2.2. Влияние параметров нормального закона распределения на вероятность безотказной работы (а), плотность распределения наработки до отказа (б), интенсивность отказов (в)

Вывод: при нормальном законе распределения при увеличении параметра m (математического ожидания) вероятность безотказной работы увеличивается, наибольшие значения плотности отказов наступают через определенный интервал времени, также интенсивность отказов увеличивается через определенный интервал времени. При увеличении параметра σ вероятность безотказной работы сначала уменьшается, затем увеличивается, плотность и интенсивность отказов уменьшаются.

Лабораторная работа 3

НАДЕЖНОСТЬ ПРОСТЕЙШЕЙ СИСТЕМЫ ПРИ ОСНОВНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ

Ц е л ь р а б о т ы: изучить показатели надежности простейшей системы при основном соединении ее элементов, дать оценку влиянию общего количества элементов на основные показатели надежности простейшей системы.

Исходные данные количество и интенсивность отказов элемента простейшей системы при основном соединении: n = 2; λ = 0,24