эвм. ЭВМ. Найдем расстояние между точкой a 5
 Скачать 77.25 Kb. Скачать 77.25 Kb.
|
Практическое задание
Пермь 2020 Задание №1. Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти: а) уравнение стороны АС; б) длину высоты, проведенной из вершины А; в) величину угла В (в радианах). А) AC= 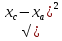 +( +(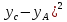 = =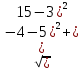 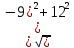 = =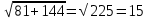 Б) Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины: 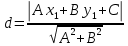 Найдем расстояние между точкой A(5;3) и прямой BC (7y -24x - 201 = 0) d 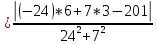 d = 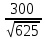 =12 =12Расстояние между двумя точками выражается через координаты формулой: 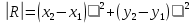 Задание № 2. Даны вершины А1(7; 0; 3), A2(3; 0; -1), A3(3; 0; 5), A4(4; 3; -2). Средствами векторной алгебры найти: а) длину ребра А1A2; б) угол между ребрами А1A2 и А1A3; в) площадь грани А1A2A3; г) длину высоты пирамиды, проведенной из вершины A4; д) объем пирамиды А1A2A3A4. А) Длина вектора a(X;Y;Z) выражается через его координаты формулой: 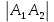 = =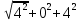 = =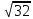 =5.657 =5.657Б) Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле 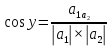 где a1a2 = X1X2 + Y1Y2 + Z1Z2 где a1a2 = X1X2 + Y1Y2 + Z1Z2Найдем угол между ребрами A1A2(-4;0;-4) и A1A3(-4;0;2): 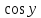 = =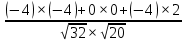 γ = arccos(0.316) = 71.5670 В) Площадь грани можно найти по формуле: 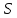 = =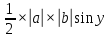 где где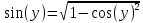 Найдем площадь грани A1A2A3 Найдем угол между ребрами A1A2(-4;0;-4) и A1A3(-4;0;2) 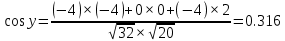 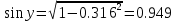 Площадь грани A1A2A3 SA1A2A3 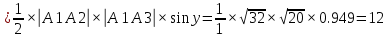 Найдём площадь грани с учётом геометрического смысла векторного произведения: 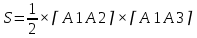 Векторное произведение:
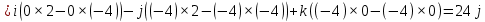 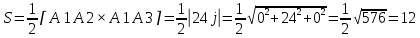 Г) Длину высоты пирамиды, проведенной из вершины A4 Расстояние d от точки M1(x1;y1;z1) до плоскости Ax+By+Cz+D  0 равно абсолютному значению величины: 0 равно абсолютному значению величины: 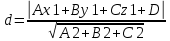 Уравнение плоскости A1A2A3:y 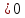 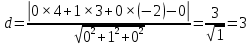 Д) объем пирамиды А1A2A3A4. Объем пирамиды, построенный на векторах a1(X1;Y1;Z1) , a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
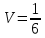
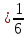  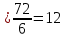 Где определитель матрицы равен: 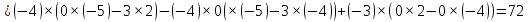 Задание № 3. Найти матрицу С = 3А - 2В, где A 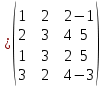 , B , B 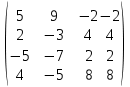 3 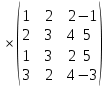 -2 -2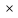 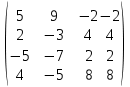 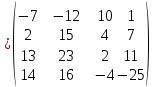 Задание № 4. Решить систему линейных алгебраических уравнений. 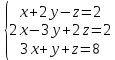 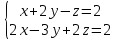 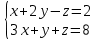 4x+y 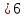 4x+3y 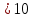 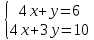 X 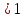 Y 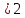 1+2 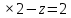 z 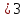 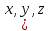 ) )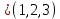 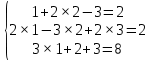 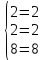 (x,y,z) 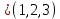 Задание № 5. Вычислить площадь фигуры, ограниченной линиями y = x2 – 4x + 3 и y = x – 1. Построить график. исследуем функцию y₁ = x² - 4x + 3 Нули функции: x² - 4x + 3 = 0 D = 16 - 12 = 4 √D = 2 x₁ = (4 - 2):2 = 1 x₂ = (4 + 2):2 = 3 Вершина параболы: х = 4/2 = 2 у(2) = 4 - 4·2 + 3 = -1 Для определения пределов интегрирования найдёи точки пересечения функций y₁ = x² - 4x + 3 и y₂ = x - 1x² - 4x + 3 = х – 1 x² - 5x + 4 = 0 D = 25 - 16 = 9 √D = 3 x₁ = (5 - 3):2 = 1 x₂ = (5 + 3):2 = 4 Итак, нижний предел интегрирования x₁ = 1, верхний - x₂ = 4 Поскольку на интервале х∈(1,4) у₂ > у₁, то будем находить интеграл от разности у₂ - у₁ = x - 1 - (x² - 4x + 3) = x - 1- x² + 4x - 3 = - x² + 5x - 4 ∫(- x² + 5x - 4)dx = -x³/3 + 5x²/2 - 4x Подставим пределы интегрирования S = (-64/3 + 5·16/2 - 4·4) - (-1/3 + 5/2 - 4) = -64/3 + 40 - 16 +1/3 - 5/2 + 4 = - 21 + 28 - 2,5 = 4,5 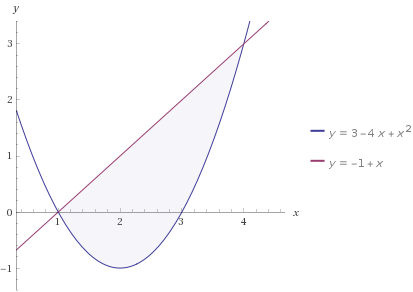 Задание № 8. Транспортная задача. Постановка задачи: на складах А1, А2, А3 имеются запасы продукции в количествах 180, 300, 120 т. соответственно. Потребители В1, В2, В3 должны получить эту продукцию в количествах 110, 350, 140 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы матрицей С (ден. ед.) 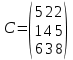 Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 180 + 300 + 120 = 600 ∑b = 110 + 350 + 140 = 600 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Занесем исходные данные в распределительную таблицу. Этап I. Поиск первого опорного плана. 1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Искомый элемент равен c21=1. Для этого элемента запасы равны 300, потребности 110. Поскольку минимальным является 110, то вычитаем его. x21 = min(300,110) = 110.
Искомый элемент равен c12=2. Для этого элемента запасы равны 180, потребности 350. Поскольку минимальным является 180, то вычитаем его. x12 = min(180,350) = 180.
Искомый элемент равен c32=3. Для этого элемента запасы равны 120, потребности 170. Поскольку минимальным является 120, то вычитаем его. x32 = min(120,170) = 120.
Искомый элемент равен c22=4. Для этого элемента запасы равны 190, потребности 50. Поскольку минимальным является 50, то вычитаем его. x22 = min(190,50) = 50.
Искомый элемент равен c23=5. Для этого элемента запасы равны 140, потребности 140. Поскольку минимальным является 140, то вычитаем его. x23 = min(140,140) = 140.
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи. 2. Подсчитаем число занятых клеток таблицы, их 5, а должно быть m + n - 1 = 5. Следовательно, опорный план является невырожденным. Значение целевой функции для этого опорного плана равно: F(x) = 2*180 + 1*110 + 4*50 + 5*140 + 3*120 = 1730 Этап II. Улучшение опорного плана. Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v2 = 2; 0 + v2 = 2; v2 = 2 u2 + v2 = 4; 2 + u2 = 4; u2 = 2 u2 + v1 = 1; 2 + v1 = 1; v1 = -1 u2 + v3 = 5; 2 + v3 = 5; v3 = 3 u3 + v2 = 3; 2 + u3 = 3; u3 = 1
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij (1;3): 0 + 3 > 2; ∆13 = 0 + 3 - 2 = 1 > 0 Выбираем максимальную оценку свободной клетки (1;3): 2 Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
Цикл приведен в таблице (1,3 → 1,2 → 2,2 → 2,3). Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 140. Прибавляем 140 к объемам грузов, стоящих в плюсовых клетках и вычитаем 140 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v2 = 2; 0 + v2 = 2; v2 = 2 u2 + v2 = 4; 2 + u2 = 4; u2 = 2 u2 + v1 = 1; 2 + v1 = 1; v1 = -1 u3 + v2 = 3; 2 + u3 = 3; u3 = 1 u1 + v3 = 2; 0 + v3 = 2; v3 = 2
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij. Минимальные затраты составят: F(x) = 2*40 + 2*140 + 1*110 + 4*190 + 3*120 = 1590 Анализ оптимального плана. Из 1-го склада необходимо груз направить к 2-у потребителю (40 ед.), к 3-у потребителю (140 ед.) Из 2-го склада необходимо груз направить к 1-у потребителю (110 ед.), к 2-у потребителю (190 ед.) Из 3-го склада необходимо весь груз направить к 2-у потребителю |
