Выборка_3. Найти доверительный интервал для математического ожидания с надежностью 0,99

• Название: Найти доверительный интервал для математического ожидания с надежностью 0,99
• Дата: 11.11.2022
• Размер: 83.83 Kb.
• Имя файла: Выборка_3.docx
• Тип: Документы; #783344

Задание 9.

Даны значения признака X, полученные в результате выборочного обследования совокупности. Требуется:

1. 
   построить интервальный вариационный ряд частот с равными интервалами, выбрав число интервалов 8 или 9;
   
2. 
   построить гистограмму частот;
   
3. 
   построить дискретный вариационный ряд, соответствующий интервальному;
   
4. 
   найти эмпирическую функцию распределения по дискретному ряду;
   
5. 
   построить график эмпирической функции распределения;
   
6. 
   вычислить выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение;
   
7. 
   вычислить теоретические частоты по интервальному вариационному ряду выборки, предположив, что случайная величина X распределена нормально;
   
8. 
   используя критерий Пирсона при уровне значимости =0,01, проверить гипотезу о нормальном распределении случайной величины X;
   
9. 
   найти доверительный интервал для математического ожидания с надежностью =0,99
   

68	76		79		90		80		82		78		71		80		81
80	79		74		78		70		77		72		73		76		78
79	81		80		77		82		83		79		66		71		72
78	80		77		75		73		89		77		81		88		79
78	74		67		75		76		78		86		84		75		87

Решение.

1. 
   Построим интервальный вариационный ряд частот с равными интервалами, выбрав число интервалов 8.
   

Число наблюдений

Число интервалов

Длина интервала

Итак, интервальный вариационный ряд имеет вид:

Интервалы	(66-69]	(69-72]	(72-75]	(75-78]	(78-81]	(81-84]	(84-87]	(87-90]
Частоты	3	5	7	13	13	4	2	3

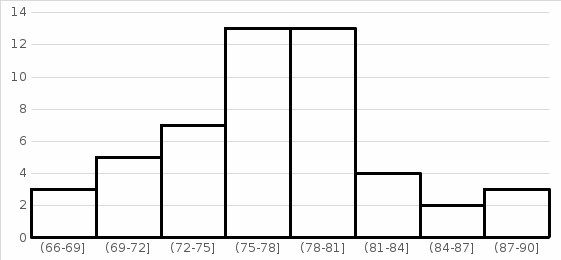Рис.1. Гистограмма частот

2) Дискретный вариационный ряд, соответствующий данному интервальному ряду, записываем в таблицу.

Интервальный ряд:

Интервал	Частота
48-50	3
50-52	4
52-54	10
54-56	10
56-58	8
58-60	7
60-62	5
62-64	3
	50

2. 
   Построим гистограмму частот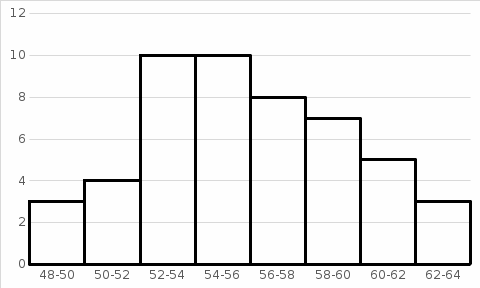
   

Рис.1. Гистограмма

3. 
   Построим дискретный вариационный ряд, соответствующий интервальном, приняв за середины интервалов.
   

			Относительные частоты,
1	67,5	3	0,06
2	70,5	5	0,1
3	73,5	7	0,14
4	76,5	13	0,26
5	79,5	13	0,26
6	82,5	4	0,08
7	85,5	2	0,04
8	88,5	3	0,06

Геометрической интерпретацией дискретного вариационного ряда является полигон относительных


Рис. 3. Полигон относительных частот

4. 
   Найдем эмпирическую функцию распределения по дискретному ряду
   

Рассчитаем накопленные относительные частоты

Интервал				Накопленные относительные частоты
1	67,5	3	0,06	0,06
2	70,5	5	0,1	0,16
3	73,5	7	0,14	0,3
4	76,5	13	0,26	0,56
5	79,5	13	0,26	0,82
6	82,5	4	0,08	0,9
7	85,5	2	0,04	0,94
8	88,5	3	0,06	1

Функция распределения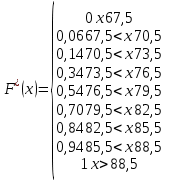

5. 
   Построим график эмпирической функции распределения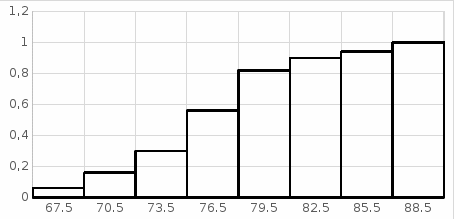
   

Рис.4. График эмпирической функции распределения

6. 
   Числовые характеристики дискретного вариационного ряда
   

1	67,5	3	202,5	13668,75
2	70,5	5	352,5	24851,25
3	73,5	7	514,5	37815,75
4	76,5	13	994,5	76079,25
5	79,5	13	1033,5	82163,25
6	82,5	4	330	27225,00
7	85,5	2	171	14620,50
8	88,5	3	265,5	23496,75
		50	3864	299920,5

Выборочная средняя:

Дисперсия



Cреднеквадратическое отклонение

7. 
   Вычислим теоретические частоты по интервальному вариационному ряду выборки, предположив, что случайная величина X распределена нормально
   

Вычисления проведем по формулам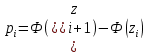







значения функции Лапласа

66	69	3	-	-1,617	-0,500	-0,447	0,053	2,6
69	72	5	-1,617	-1,031	-0,447	-0,349	0,098	4,9
72	75	7	-1,031	-0,445	-0,349	-0,172	0,177	8,8
75	78	13	-0,445	0,141	-0,172	0,056	0,228	11,4
78	81	13	0,141	0,727	0,056	0,266	0,210	10,5
81	84	4	0,727	1,313	0,266	0,405	0,139	7,0
84	87	2	1,313	1,899	0,405	0,471	0,066	3,3
87	90	3	1,899	-	0,471	0,500	0,029	1,4
		50					1,000	50

8. 
   Используя критерий Пирсона при уровне значимости =0,01, проверим гипотезу о нормальном распределении случайной величины X
   

1	3	2,6	0,0475
2	5	4,9	0,0015
3	7	8,8	0,3837
4	13	11,4	0,2263
5	13	10,5	0,5861
6	4	7,0	1,2545
7	2	3,3	0,5074
8	3	1,4	1,6879
	50	50	4,695

Наблюдаемое значение критерия Пирсона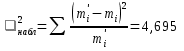

Критическое значение 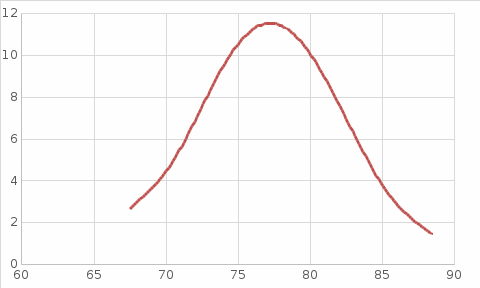(=0,01;k=s-3)= (=0,05;k=8-3) =15,1

нулевая гипотеза о том, что СВ X распределена по нормальному закону принимается.

9. 
   Найдем доверительный интервал для математического ожидания с надежностью =0,99
   

Доверительный интервал для математического ожидания



γ=0,99 t=2,58



Задание 10.

По заданной корреляционной таблице найти числовые характеристики статистического распределения, групповые средние, написать уравнение прямой регрессии Y по X, построить эмпирическую линию регрессии и прямую регрессии, оценить тесноту связи.

Y\X	2	4	6	8	10	12
5	5	1					6
15		6	2	5			13
25			5	40	5		50
35			2	8	9		19
45				4	5	3	12
	5	7	9	57	19	3	n=100

Решение

Найдем числовые характеристики







Cоставим расчетные таблицы.

2	5	10	20		5	6	30	150
4	7	28	112		15	13	195	2925
6	9	54	324		25	50	1250	31250
8	57	456	3648		35	19	665	23275
10	19	190	1900		45	12	540	24300
12	3	36	432
Сумма	100	774	6436			100	2680	81900

Каждому значению переменной Х поставим в соответствие среднее значение переменной Y:















Уравнение регрессии





уравнение регрессии

Коэффициент корреляции

Близость коэффициента корреляции к единице говорит о тесной линейной зависимости между составляющими Х и Y.

Найдем значение Ф(a,b)

2	5	5,00	6,34	9,02
4	7	13,57	13,47	0,07
6	9	25,00	20,60	174,34
8	57	26,93	27,73	36,19
10	19	35,00	34,85	0,40
12	3	45,00	41,98	27,32
	100			247,337

Построим обе линии регрессии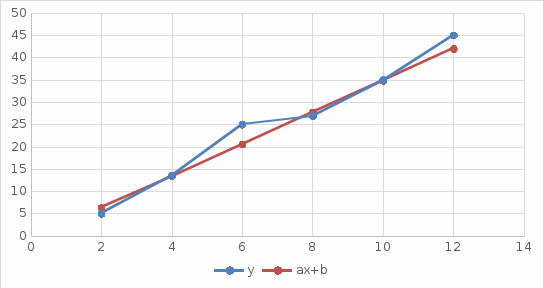



Рис.5. Эмпирическая и прямая линии регрессии