Математика 1 курс итоговое. Математика итоговое задание. Найти область определения, точки

• Название: Найти область определения, точки
• Анкор: Математика 1 курс итоговое
• Дата: 26.12.2022
• Размер: 50.38 Kb.
• Имя файла: Математика итоговое задание.docx
• Тип: Документы; #864603

Задание. Для функции 𝑦 = (2𝑥 + 3)𝑒^5𝑥 :

1. 
   Найти область определения, точки разрыва.
   
2. 
   Исследовать функцию на четность, периодичность.
   
3. 
   Исследовать поведение функции на концах области определения. Указать асимптоты.
   
4. 
   Найти промежутки монотонности. Точки экстремума.
   
5. 
   Найти промежутки выпуклости. Точки перегиба.
   
6. 
   Найти площадь фигуры, ограниченной графиком функции
   

𝑦 = ⁽2𝑥 + 3⁾𝑒^5𝑥 и прямыми 𝑥 = 0, 𝑥 = 2, 𝑦 = 0.

Результаты исследования оформить в виде таблицы.

Область определения:	(-∞;+∞)
Четность, периодичность:	Ни четная, ни нечетная; непериодическая
Поведение на концах области определения:	При х→-∞ предел функции равен 0, При х→+∞ предел функции ∞
Асимптоты:	Горизонтальных и наклонных асимптот нет
Промежутки монотонности:	убывает (-∞;-1,7), возрастает (-1,7;+ ∞)
Точки экстремума:	(-1,7; -0,4e^(-8.5))
Промежутки выпуклости:	Вогнутость [-1,9;+ ∞), Выпуклость (-∞; -1,9]
Точки перегиба:	(-1,9; -2e^-9,5)
Площадь криволинейной трапеции.	-0,58+17,8е10

1. Область определения: функция непрерывна на всем промежутке (-∞;+∞).

2. Четность, нечетность и периодичность:

у(-х)=(-2х-3)е^-5х≠у(х) значит функция не обладает свойствами четности и нечетности. Функция является функцией общего вида, поэтому не периодическая.

3. y = (2·x-3)·e^5·x
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:

Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

4. Промежутки монотонности:

Найдем производную функции:

у^/=2е^5х+5(2х+3)е^5х

2е^5х+5(2х+3)е^5х=0

е^5х(10х+15)=0

10х+17=0

х=-1,7

значит функция убывает (-∞;-1,7), возрастает (-1,7;+ ∞)

5. Точки экстремума:

у(-1,7)=(2*(-1,7)+3)^-8,5=-0,4е^-8,5

(-1,7; -0,4e^-8,5) – точка минимума функции

6. Промежутки выпуклости:

Найдем вторую производную:

у^//=10е^5х+10е^5х+25(2х+3)е^5х=20е^5х+25(2х+3)е^5х

20е^5х+25(2х+3)е^5х=0

е^5х(95+50х)=0

95+50х=0

х=-1,9

значит: вогнутость (-1,9;+ ∞), выпуклость (-∞; -1,9)

7. Точки перегиба

у(-1,9)=-2е^-9,5

(-1,9; -2e^-9,5) – единственная точка перегиба.

Построим график функции: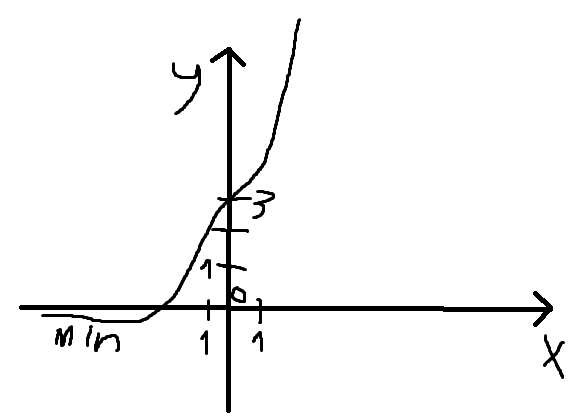


7. Найти площадь фигуры, ограниченной графиком функции

𝑦 = ⁽2𝑥 + 3⁾𝑒^5𝑥 и прямыми 𝑥 = 0, 𝑥 = 2, 𝑦 = 0.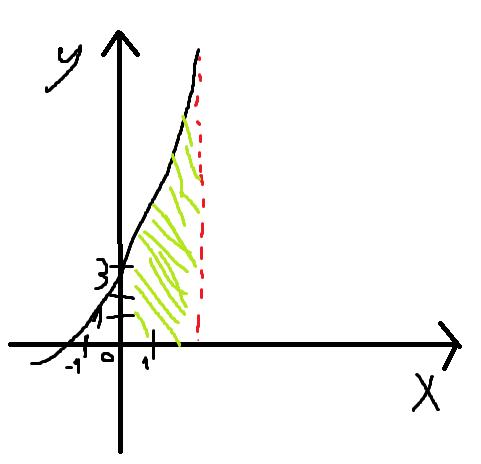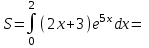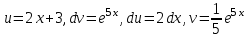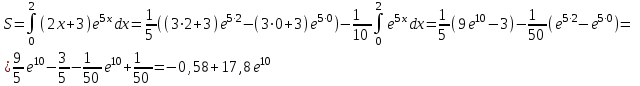