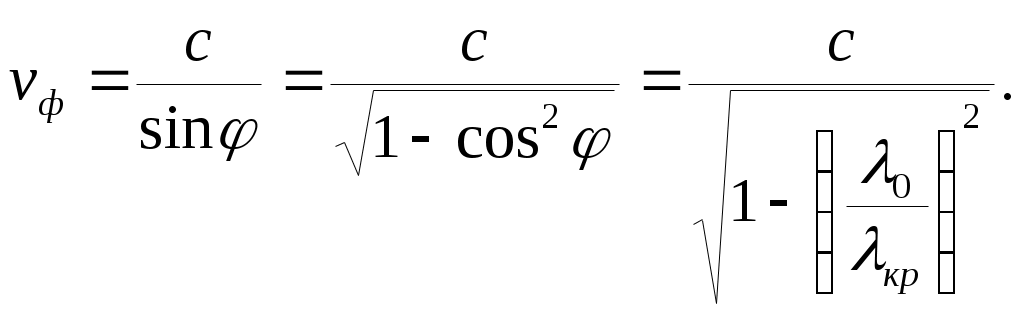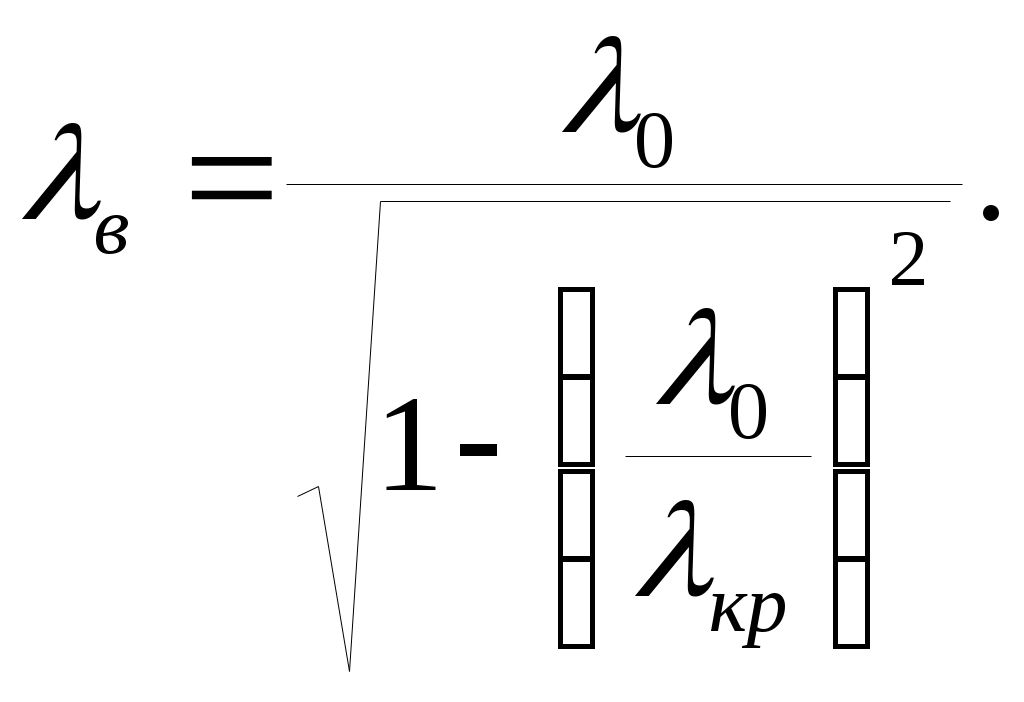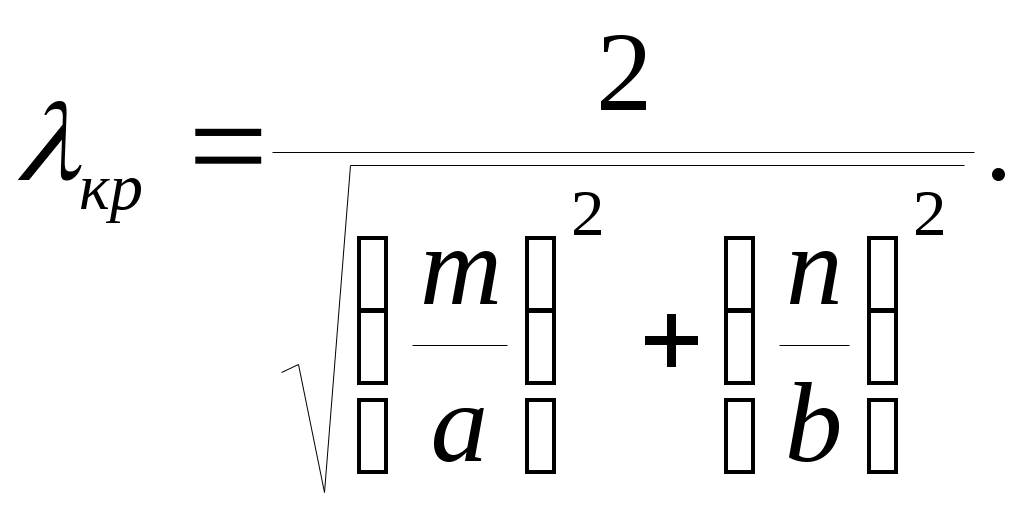Напр. направляющие. Направляемые волны и направляющие системы
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
3.1. Критическая длина волны в плоском волноводе Выясним условия существования различных мод волн в зависимости от их индекса, ширины волновода и длины волны возбуждения. Длиной волны возбуждения называется такая, которую будет иметь волна той же частоты в безграничном пространстве со свойствами среды заполнения волновода При решении этой задачи будем исходить из сформулированного ранее условия существования направляемых волн в плоском волноводе. Для существования направляемых волн в плоском волноводе расстояние между плоскостями должно быть кратно половине длины волны В математической форме это условие описывается следующим выражением:
Эта формула связывает параметры волновода и волны. Нам надо соотнести угол отражения с остальными параметрами. Для этого перепишем условие (3.1) в следующем эквивалентном виде:
Длина волны возбуждения определяется путем деления фазовой скорости волны на частоту колебания, которое мы описываем. Длиной волны возбуждения называется длина волны в свободном пространстве со свойствами среды заполнения волновода. В данном случае мы приняли, что между пластинами вакуум, параметрам которого соответствует нижний индекс 0. Все величины, входящие в правую часть формулы (3.2), фиксированы. Индекс m выбирается заранее, длина волны возбуждения определяется частотой колебания, а расстояние между пластинами волновода задается его конструкцией. Изменяться может только угол отражения. Эта особенность формулы (3.2) позволяет сделать следующий вывод. При фиксированной длине волны возбуждения и расстоянии между стенками волновода каждому индексу моды соответствует значение угла падения, обеспечивающее выполнение условия существования направляемых волн Однако условие (3.2) может быть выполнено не всегда. Левая часть этого соотношения не может быть больше 1 и для любого индекса моды найдется такая длина волны возбуждения, что условие (3.2) будет выполняться только при cos φ = l. Такую длину волны называют критической. Критической называется самая большая длина волны моды колебания, которая может существовать в волноводе заданной ширины Формула для ее вычисления получается из выражения (3.2) подстановкой единицы вместо косинуса:
Если длина волны возбуждения больше критической, то эта мода колебания в волноводе существовать не может из-за того, что граничные условия на стенках волновода не будут выполняться ни при каком вещественном значении угла падения и энергия электромагнитного поля рассеется в металле волновода. На критической длине волны в волноводе происходит следующее. Так как угол падения равен нулю, в поперечной плоскости образуется стоячая волна. Волнового движения и переноса энергии вдоль оси z нет, и колебания вдоль всего волновода происходят в фазе. Это явление можно трактовать как бесконечную фазовую скорость. При длине волны возбуждения, равной критической, продольное волновое число равно нулю, а фазовая скорость бесконечна Из этих рассуждений можно сделать следующий вывод. Каждая мода колебания может существовать как бегущая волна в области длин волн, меньших критической Значит, для того чтобы волна распространялась в волноводе, должно выполняться следующее неравенство:
Волны длиннее критической по волноводу распространяться не могут. Поэтому весь диапазон длин волн обычно делят. Областью прозрачности называется часть диапазона, в которой длина волны возбуждения меньше критической Областью отсечки называется часть диапазона, в которой длина волны возбуждения больше критической Границей между ними является критическая длина волны. В большинстве случаев из всех мод наиболее важна та, у которой критическая длина волны максимальна. Она называется основной. Основной называется мода, обладающая наибольшей критической длиной волны В плоском волноводе основных мод волн две - E1 и H1. Для них λкр = 2а. Таким образом, если длина волны возбуждения превосходит удвоенную ширину плоского волновода, то такая волна распространяться в волноводе не будет. Если длина волны возбуждения меньше удвоенной ширины волновода, но не меньше ширины, то в волноводе могут существовать только волны основных мод. В математической форме это условие записывается следующим образом:
При длине волны возбуждения меньшей, чем ширина волновода, появляется возможность возникновения еще двух мод волн, Е2 и Н2, но при этом могут существовать и основные моды. Если и дальше повышать частоту, то есть уменьшить длину волны возбуждения, появится возможность распространения волн с нижними индексами 3, затем 4 и так далее. Однако возможность распространения мод с меньшими индексами сохраняется. 3.2. Фазовая скорость и длина волны в волноводе Знание критической длины волны позволяет определить фазовую скорость для заданной длины волны возбуждения при любом индексе моды колебания:
Эта формула весьма показательна. Если длина волны возбуждения больше критической, под корнем в знаменателе получится отрицательное число, а корень из отрицательного числа мнимый. Значит, мнимой станет фазовая скорость и распространяющейся волны не будет. При длине волны возбуждения меньше критической под корнем будет действительное число меньше единицы. Фазовая скорость также станет действительным числом, большим, чем скорость света в вакууме и волна будет распространяться. Фазовая скорость продольных волн, распространяющихся в волноводе, больше скорости света Это происходит из-за того, что продольная волна в волноводе распространяются за счет многократного отражения от стенок. Значит, от начала до конца волновода ее фронт пройдет путь, превышающий физическую длину волновода. Если длина волны возбуждения будет равна критической, под корнем получается нуль и фазовая скорость станет бесконечно большой. В этом случае волна существует в волноводе, но не распространяется. Отличительной особенностью этой формулы является ее универсальность: фазовая скорость зависит только от отношения длин волн возбуждения и критической. Значит, формула (3.6) применима для вычисления фазовой скорости волн в любом полом металлическом волноводе. Для определения длины волны в волноводе фазовую скорость надо разделить на частоту. Получим:
Формулы (3.6) и (3.7) получены в предположении о том, что пространство между плоскостями заполнено вакуумом. Если заполнение будет иным, иными будут исходная фазовая скорость и длина волны. 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ НАПРАВЛЯЮЩИХ СИСТЕМ НА БАЗЕ ПЛОСКОГО ВОЛНОВОДА Мы изучили распространение электромагнитных волн в плоском волноводе и установили, что при определенных условиях в нем могут распространяться продольные Е- и Н-волны, а так же поперечная Т-волна. Однако плоский волновод не имеет практического значения так как его поперечные размеры не ограничены и плотность энергии остается бесконечно малой. Значит, надо уменьшить область существования поля. Для этого можно перпендикулярно имеющимся плоскостям вдоль направления распространения волны установить две перегородки из идеального проводника. В результате получится полый металлический волновод прямоугольного сечения. При этом характеристики исходной системы, плоского волновода, изменились. Плоский волновод состоял из двух изолированных проводников, а в прямоугольном волноводе остался только один. По этому признаку, количеству изолированных проводников, направляющие системы делятся на односвязные и многосвязные. Односвязной называется направляющая система, состоящая из одного проводника Односвязная направляющая система, полый металлический волновод, может иметь любую форму поперечного сечения. Полым металлическим волноводом называется труба произвольного сечения, изготовленная из материала с высокой электропроводностью В нашем случае волновод получился прямоугольным. Это одна из наиболее часто встречающихся форм поперечного сечения. Кроме прямоугольного, для передачи электромагнитной энергии используются волноводы круглого, эллиптического, Г-образного, П-образного и Н-образного. Однако поперечное сечение трубы может быть любым. Нет физических причин для того, чтобы в металлической трубе любого сечения не могли распространяться электромагнитные волны, отвечающие определенным требованиям. В полых металлических волноводах волны распространяются за счет многократного отражения от стенок, то есть имеет место быть полная аналогия с распространением Е- и Н-волн в плоском волноводе. Следовательно, в полом металлическом волноводе могут распространяться только продольные волны, а длина волны возбуждения должна быть меньше критической. От формы поперечного сечения зависит только способ вычисления критической частоты. Плоский металлический волновод с Т-волной является прототипом многосвязной направляющей системы, в структуре которой изолированных проводников должно быть не менее двух. Многосвязной называется направляющая система, имеющая в своем составе более одного изолированного проводника Наиболее распространены двухсвязные системы, то есть системы с двумя проводниками. Это двухпроводная, коаксиальная и полосковая линии, однако в полосковой линии количество изолированных проводников может быть и больше двух. Таким образом, в направляющих системах, теория работы которых опирается на плоский волновод, могут распространяться продольные Е- и Н-волны и поперечные Т-волны. Фазовая скорость Е- и Н-волн в полых металлических волноводах больше фазовой скорости волн в свободном пространстве со свойствами среды заполнения волновода. Такие направляющие системы называются волноводами быстрых волн. Волноводом быстрых волн называется направляющая система, в которой фазовая скорость волн больше скорости в свободном пространстве Т-волна в многосвязной направляющей системе имеет такие же характеристики, как и поперечная волна в свободном пространстве. Такие волноводы называются волноводами Т-волн. Волноводом Т-волн называется направляющая система, в которой фазовая скорость волн равна скорости в свободном пространстве В них волна распространяется без отражения от направляющих проводников. Однако есть еще один способ создания волноводов. Известно, что вдоль границы с оптически менее плотной средой может распространяться направляемая волна. Граница с оптически менее плотной средой – это, например, граница между диэлектриком и воздухом, если волна падает из диэлектрика. Этот эффект позволяет создавать диэлектрические волноводы. В них фазовая скорость волн меньше, чем в окружающем пространстве, поэтому они называются волноводами медленных волн. Волноводом медленных волн называется направляющая система, в которой фазовая скорость волн меньше, чем в окружающем пространстве Волноводы медленных волн будут описаны далее, а в настоящем разделе коротко рассмотрены основные характеристики направляющих систем на основе плоского волновода. При этом упор сделан не на описания деталей, а на основных принципах и особенностях их работы. 4.1. Полые металлические волноводы Полые металлические волноводы – это металлические трубы. Электромагнитная волна может распространяться в трубах с любой формой поперечного сечения, однако она должна отвечать двум требованиям: волна должна быть продольной; ее частота должна быть выше критической. Волны в полых металлических волноводах распространяются так же, как продольные волны в плоском волноводе, то есть за счет многократных отражений от стенок. При этом путь, проходимый фронтом волны в волноводе, больше его физической длины и фазовая скорость больше фазовой скорости волны в свободном пространстве. Длина волны в волноводе, длины волны возбуждения и критическая длина волны связаны между собой дисперсионным уравнением:
Это уравнение показывает, что при изменении длины волны возбуждения длина волны в волноводе изменяется не пропорционально ей. Решив его, легко получить формулу (3.6) для вычисления длины волны в волноводе, которая была получена из иных соображений для плоского волновода. Следовательно, дисперсионное уравнение (4.1), формула (3.6) для вычисления λв и формула (3.7) для фазовой скорости являются универсальными и пригодны для расчета характеристик волны при любой форме поперечного сечения волновода. Прямоугольный волновод - это металлическая труба прямоугольного поперечного сечения. При решении задачи распространения электромагнитной волны в волноводе принимается допущение, позволяющее на первом этапе не учитывать потери: волновод заполнен вакуумом, а стенки изготовлены из материала с бесконечно большой электропроводностью. Для описания поля в волноводе необходимо решить волновые уравнения с учетом граничных условий - равенства нулю тангенциальных составляющих вектора напряженности электрического поля на контуре его поперечного сечения. Эти уравнения решаются методом разделения переменных В результате решения уравнений достаточно получить формулы только для продольных составляющих поля, так как поперечные составляющие могут быть определены дифференцированием по формулам перехода (2.37) – (2.40). Критическая длина моды волны в прямоугольном волноводе описывается формулой:
Сравните эту формулу с формулой (3.3) для критической длины волны в плоском волноводе. Там был один размер волновода а и одно число полуволн поперечной стоячей волны между стенками волновода m. В прямоугольном волноводе есть еще один размет b, по которому также может существовать резонанс. Число n означает количество полуволн стоячей волны, возникшей вдоль второго размера волновода. Числа m и n называются индексами моды волны. Они означают количество полуволн стоячих волн, существующих вдоль широкой и узкой стенок волновода соответственно. Так как величины индексов не ограничены, в полом металлическом волноводе может существовать бесконечно много мод волн. Выясним вопрос о том, какая мода является основной в прямоугольном волноводе, то есть какая мода имеет максимальную критическую длину волны. Из формулы (4.2) следует, что при фиксированных размерах волновода наибольшую критическую длину волны будет иметь та мода, которой соответствуют наименьшие индексы. Теоретически наименьшая величина индекса моды – нуль. Однако оба индекса моды не могут быть равны нулю: для существования продольной волны необходим резонанс хотя бы по одному размеру волновода. Индекс моды n обычно соответствует меньшей стенке волновода, ширина которой обычно обозначается b, а индекс m – большей, ширина которой обычно обозначается а. Значит, нулю должен быть равен индекс n: при m = 1, а n = 0 критическая длина волны будет больше, чем при m = 0, а n = 1. Следовательно, в прямоугольном волноводе основной волной будет мода с нижним индексом 10, то есть такая, у которой вдоль широкой стенки возникнет одна полуволна стоячей волны, а вдоль узкой поле однородно. В плоском волноводе основных мод было две, Е1 и Н1. В прямоугольном волноводе основная волна будет только одна, Н10. Основной волной в прямоугольном волноводе является мода Н10 Это обусловлено тем, что на стенках волновода должно выполняться граничное условие - касательная составляющая вектора напряженности электрического поля обращается в нуль. У Е-волны касательной к стенкам является не только поперечная, но и продольная составляющая вектора напряженности электрического поля. Поэтому резонансы должны существовать вдоль обеих стенок: если вдоль одной из них поле будет однородным, граничное условие не будет выполняться. Следовательно, электрическая волна, у которой хотя бы один из индексов равен нулю, существовать не может. Круглый металлический волновод представляет собой трубу в форме кругового цилиндра с внутренним радиусом а. Задачу описания поля в круглом волноводе надо решать в цилиндрической системе координат, поэтому поперечное распределение поля описывается цилиндрическими функциями первого рода, которые называются функциями Бесселя и обозначаются Jm(x), где m – называется индексом функции. Моды волн в цилиндрическом волноводе обозначаются так же, как и в электрическом, то есть буквами Е или Н с нижним индексом из двух чисел. Однако физический смысл индексов моды волны иной. Величина индекса m означает число вариаций поля по угловой координате φ, а величина индекса n - число вариаций по радиальной координате r Индекс m – это индекс функции Бесселя. В частном случае при m = 0 поле однородно по углу φ. Такие моды называют симметричными. Индекс n – это номер нуля функции Бесселя или ее производной. Следовательно, он не может быть равен нулю. Критические длины волн в круглом волноводе описываются разными формулами. Для электрических мод:
Для магнитных мод:
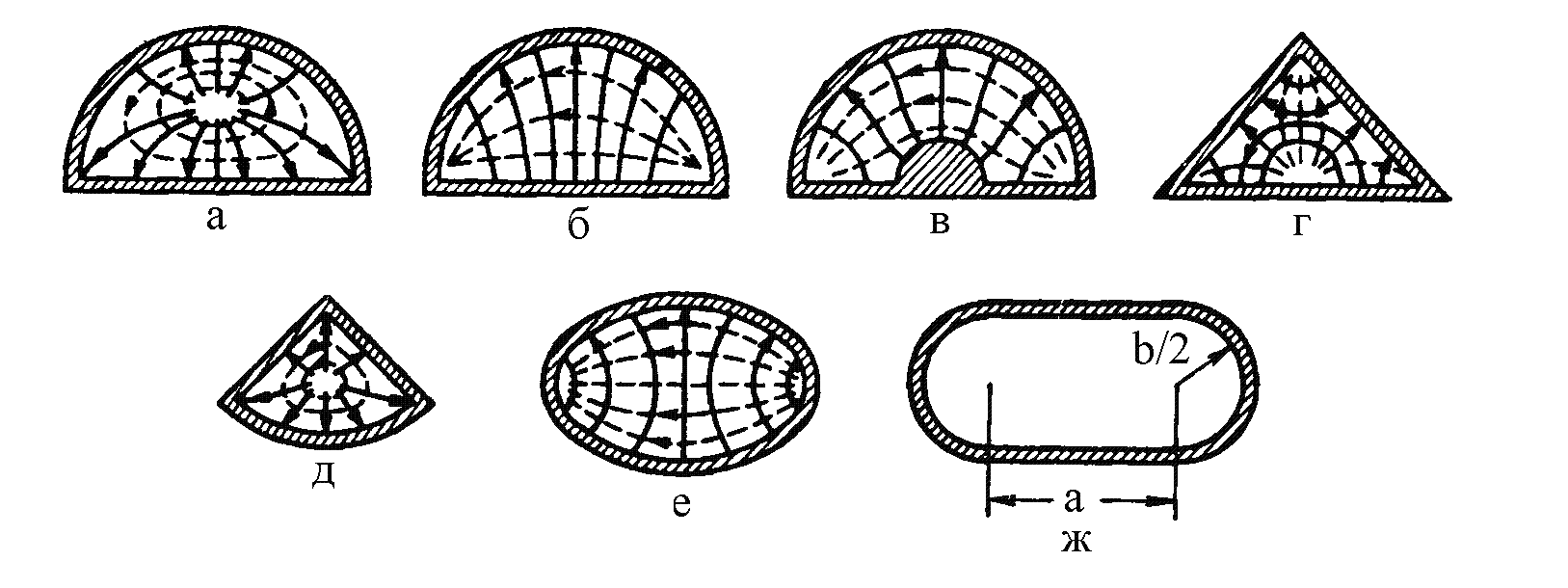
Основную волну цилиндрического волновода можно определить по таблицам нулей функции Бесселя и ее первой производной. В них надо выбрать такой номер нуля, для которого значение аргумента минимально. Минимальное значение координаты соответствует первому нулю производной функции Бесселя индекса 1. То есть основной волной круглого волновода является волна Н11. Основной волной круглого волновода является мода Н11 Кроме прямоугольного и круглого волноводов существуют и иные, со сложной формой поперечного сечения. Примеры сечений таких волноводов приведены на рис. 4.1.
Такие волноводы могут иметь лучшие характеристики по сравнению с прямоугольными и круглыми. Однако их использование встречает определенные трудности. Во-первых, это трудности изготовления. Внутренние размеры волновода должны иметь минимальное отклонение от расчетных, и высокую чистоту обработки поверхности. Очевидно, что чем сложнее форма поперечного сечения, тем труднее выполнить эти требования. Во-вторых, распределение поля в них очень сложно описать аналитически. Самые сложные функции, используемые при описании распределения поля в прямоугольном волноводе – sin и cos. В круглом волноводе поле описывается с помощью функций Бесселя, что создает дополнительные трудности при выполнении вычислений. Из всех форм поперечных сечений волноводов, изображенных на рис. 4.1, аналитическое решение получено только для эллиптического волновода (е). При этом используются эллиптические функции, которые еще сложнее, чем функции Бесселя. Однако в некоторых случаях удается получить качественное решение. Для этого необходимо взять волновод, поле в котором легко рассчитывается или известно, и мысленно или графически деформировать его стенки так, чтобы получить требуемую конфигурацию поперечного сечения. Деформация должна производиться постепенно при выполнении двух условий: силовые линии электрического поля должны быть всегда перпендикулярны стенкам волновода, а силовые линии магнитного поля - перпендикулярны силовым линиям поля электрического. Так построено поле в волноводах на рис. 4.1, а – д. Описание поля в волноводах, изображенных на рис. 4.2, з – м, производится путем разбиения волноводов сложной формы на несколько прямоугольных частей, решения волновых уравнений для каждой части отдельно и получение результирующего поля путем учета граничных условий в местах стыков частей. |